Начально-конечная задача для линейной системы Навье - Стокса

Пусть Я и S' - банаховы пространства, операторы L С £(Я; У) (т.е. линеен и непрерывен) и М Е С1(И;^) (т.е. линеен, замкнут и плотно определен). Рассмотрим линейное уравнение Соболевского типа

Ьй = Ми.                                 (0.1)

Пусть вдобавок оператор М (Др)-секториален, р € {0}UN (терминология и результаты см. гл. 3 [1]), тогда существуют вырожденные аналитические полугруппы операторов

[ R^M^dp и = f L^(M)e^dp, Jy                       27П Jy определенные на пространствах Я и ? соответственно. Введем в рассмотрение ядра ker U’ = Я0, kerF' = ?° и образы imP' = Я1, imP = S1 этих полугрупп. Нетрудно показать, что Я0 ф Я1 = Я0 ф Я1 = Я0 Ф Я1, ?° ®?’ = ?° Ф?1 = S0 Ф У1- Нам потребуется более сильное утверждение

Я°фЯх=Я f?0©?^?),                   (Al)

которое имеет место либо в случае сильной (£,р)-секториальности оператора М справа (слева), р Е {0} UN, либо рефлексивности пространства Я (?) [2]. Обозначим через L^ (Mk) сужение оператора L (М) на Я4 (domM О Я*), /г = 0,1. И если оператор М сильно (L,p}-секториален справа и слева, р Е {0} U N, то Lk Е ^(Я^; $kfi М^ Е Cl^;^), fc = 0,1, причем существует оператор М®1 Е £(5°;Я°), а также проектор Р = s — lim U*, Q = s — lim F^ расщепляющий пространство Я (?) согласно (Al), причем Я1 = imP (S1 = imQ). Введем еще одно условие - существует оператор £[’еД?1^1),                   (А2)

которое имеет место в случае сильной (Т,р)-секториальности оператора М, р € {0} UN. (Кстати, в [3] показано, что (А1) вместе с условием (Т,р)-секториальности оператора М, р Е {0} U N, дает сильную (£,р)-секториальность оператора М справа (слева), р Е {0} U N, а если к ним добавить условие (А2), то получим сильную (Т,р)-секториальность оператора М,рЕ {0} UN).

Наконец, введем еще одно важное условие -

L — спектр aL(M) оператора М представим в виде aL(M) = rfin(M) U о^М), причем rfin(M) содержится в ограниченной области Р С С с кусочно гладкой границей 7, причем 7 П crL(M) = 0.

Построим относительно спектральный проектор [4]

pfin = ^l R^dp, причем оказывается, что при условии сильной (Т,р)-секториальности оператора М справа PfinP = PPfin = Pfin- Значит, в данном случае существует проектор Pin = Р — Pfin. Итак, пусть выполнены условия (А1) - (АЗ), фиксируем т Е ВЦ., uq, ur Е 11, и для уравнения (0.1) рассмотрим начально-конечную задачу: найти вектор-функцию v Е (^“(й+ф), удовлетворяющую уравнению (0.1) и условиям

РтЫО) - и₀) = О, Р^_п(и(т) - и_т) = 0.                   (0.2)

Заметим, что если aj_in(M) = 0, то задача (0.2) превращается в задачу Шоуолтера - Сидорова Р(и(0) — ио) = 0 и поэтому считается естественным обобщением последней [5].

В настоящее время активно изучаются начально-конечные задачи для неклассических уравнений математической физики [6 - 9]. Нашей целью является постановка начальноконечной задачи для классической линейной системы уравнений Навье - Стокса и нахождение ее решения. Правда, рассмотреть эту систему нам придется несколько с иной, чем предложенная в классических монографиях [10, 11], точки зрения. Наш подход, основанный на [12], был развит в [13, 14].

• 1.    Абстрактная схема

• 2.    Конкретная интерпретация

Пусть 41 и 3" - банаховы пространства; операторы L Е £(Я; ^}, М Е С1(1р 3), причем оператор М (£,р)-секториален, р Е {0} U N, и выполнены условия (А1) - (АЗ). Тогда существуют аналитические полугруппа {IP : t Е R^} и группа {Uj_in :НЙ}, где

= Л / R^M^dp, U}in = ~ [ R^M^dp такие, что s — ^lim lP = Р и Ufin = Pfin- Построим аналитическую полугруппу {U-n : t Е R+}, где U(n = IP - и^п. Очевидно, s - P^U^ = Pin. Положим imPin(/in) = lPin{finy, очевидно, Я1 = ll]n ®llfin- Справедлива

Теорема 1. Пусть оператор М (Ь,р)-секториален, р Е {0} UN, и выполнены условия (А1) - (АЗ). Тогда при любых г Е Rj., uq, и_т Е 11 существует единственное решение задачи (0.1), (0.2), которое к тому же имеет вид u(t) = U(_nUQ + UfHu-r.

Тот факт, что вектор-функция u(t) = U(_nuo + 1Р^и_Т удовлетворяет уравнению (0.1), проверяется непосредственно. Выполнение условия (0.2) следует из соотношений Pi_nUj_in =

О и PfinUi_n = О, а также Uf_n = P_mU{_n = U{_nP_in и Ufa = Pf_inUfa = UfaP_fin при всех t € R+ в случае и*_п и при всех t 6 Кв случае Ufa. Единственность решения вытекает из эквивалентности уравнения (0.1) системе уравнений

U =0, йт = SmUm, Ufin = SfinUfini где Sin = L^Min G Cl(ilfafa) - секториальный оператор, Sfin = LfaMfin G £,{U}in^fa\, подпространства $]п и ^fa строятся аналогично пространствам [fa и ^in, только вместо полугруппы {U* : i G R+} и группы {Ufa : t G К} надо взять полугруппу {F* HGK+} и группу {Ffa :tGR}, где соответственно, операторы Lin{fin} (Min(Jifa} есть сужение операторов 1^ (MJ наЯ^^ (domMnll^).

Пусть О СК^П, n = N\{1}, - ограниченная область с границей 3Q класса С°°. В цилиндре П х К₊ рассмотрим задачу Дирихле

v(x,t) = 0, (x,t) G 5П х К+ для системы уравнений vt = vV2v — ^р, V • г = 0,                           (2.1)

которая моделирует в линейном приближении динамику вязкой несжимаемой жидкости. Прежде чем редуцировать систему (2.1) к уравнению (0.1), представим ее в виде vt = iyV2v-p, V(V-v)=0.                       (2.2)

Система (2.2) получена из (2.1) после замены Vp р [14].

Для редукции уравнений (2.2) к уравнению (0.1) нам потребуются функциональные пространства из [12]. Пусть И² и И² (Д и ЦД - подпространства соленоидальных и потенциальных вектор-функций пространства Н² = (^(0)0 Жг^))” (L² = (L²(Q))"). Формулой А = diag {V²,..., V²} задается линейный непрерывный оператор с дискретным конечнократным отрицательным спектром <т(А), сгущающимся лишь на —оо. Обозначим через ^а(тг) сужение оператора А на i^j.

Лемма 1 (теорема Солонникова - Воровича - Юдовича). Оператор А_а^ G £(tf ^рИ^]), причем а(А_а^ = сг(А) и А — А^ + А^П.

Здесь через П G £(И2,В^) обозначен проектор вдоль Н2, Е = I — П.

Лемма 2 (теорема Капитанского - Пилецкаса). Формулой В : и -^ VlV ■ и) задается оператор В G £(И²,Д), причем кет В = И².

Положим U = Je^xH_%x Д, Д = Д. Вектор u G Я имеет вид и = {и_а,и^,и_р). Формулами

/ I О О \        / »А_а  О О \

£ =   О  Н  О  , М = \  О   иА^ -К I

\ О О О /     \ О   во)

задаются операторы L G £(Д J), im£ = Д х КД х {0}, ker£ = {0} х {0} хДиМ G Cl(U; ЗД dom М = Д х Д х Д. Итак, редукция уравнений (2.2) к уравнению (0.1) закончена.

Лемма 3 [13]. При любых и € R+ оператор М сильно (Ь,1}-секториален.

Построим подпространства 11° = 5° = {0} х Ц х Нр, И1 = J1 = Иа х {0} х {0}. Выполнение условий (А1) и (А2) очевидно, причем t J О в^ \

0 V -I оА^В-^ ) ’ где В к - сужение оператора В на Н^ (из леммы 2 вытекает, что В^ : И^ —> Н^ - топлинейный изоморфизм). Нетрудно также проверить, что

M^L0 =

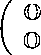
нильпотентный оператор степени 1.

Спектр ст (А) = {А^}, где А& G R_ - собственные значения, занумерованные по невозрастанию с учетом их кратности, тогда a^L(M) = {г^^-1 А&}. Понятно, что для такого множества можно подобрать контур 7 € С, который бы удовлетворял условию (АЗ).

Теперь построим

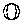
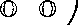
Тогда в силу теоремы 1 и леммы 3 справедлива следующая

Теорема 2. При любых у € R+, uq,u_t G И существует единственное решение задачи (0.2) для системы уравнений (2.2), причем это решение и = u(t) имеет вид

^ir(^) — Uj ^TG Т ^2^0<Т) П^- — б, Up — 0.

В заключение автор считает своим приятным долгом выразить свою искреннюю благодарность Г.А. Свиридюку за постановку задачи и интерес к работе.