Начально-конечные задачи для неклассических моделей математической физики

В настоящее время развитие современных высоких технологий приводит к необходимости исследования физических процессов, возникающих в инжиниринге. В связи с этим возникает необходимость построения адекватных математических моделей и их дальнейшее изучение. В данной статье предполагается рассмотреть следующие модели.

• I.    Пусть П с R n - ограниченная оскласть с граинней д П класса C^ . В пилиидре П х R₊ рассмотрим модель Плотникова. [1, 2]

9 t ( x, t ) + p t ( x, t ) = A 9 ( x, t ) + f ( x, t ) ,   A p ( x, t ) + ap ( x, t ) + в9 ( x, t ) + g ( x, t ) = 0 ,

(0 . 1)

(x, t) + X9(x, t) = 0, ^( (x, t) + Xp(x, t) = 0, (x, t) G дП х R+ ∂n                  ∂n которая является линеаризацией в нуле системы уравнений фазового поля, описывающих в рамках мезоскопической теории фазовые переходы первого рода. Здесь X G R, а, в G C, функции fug отвечают внешнему воздействию на систему.

• II.    Пусть теперь П с R n. n G { 2 , 3 } - ограниченная ос5.тасть с граинней д П класса C^. Система, уравнений Навье - Стокса.

v_t = vV ² v — ( v • V ) v — Vp,  V • v = 0 ,

(0 . 2)

моделирующая динамику вязкой несжимаемой жидкости, была, получена, в 1845 году. Здесь вектор-функция v = (v 1, v2,..., vn), vm = vm(x,t) соответствует скорости жидкости, функция p = p(x,t) - давлению, параметр v G R+ характеризует вязкость. За истекшее время уравнения (0.2) изучались в различных аспектах, наиболее глубокие их исследования изложены в [3, 4]. Однако до сих пор не решен вопрос о существовании сильных решений задачи Коши - Дирихле

v ( x, 0) = v о( x ) , x E fi ,

v ( x,t ) = 0 , ( x,t ) E d fi x (0 , T )

(0 . 3)

для уравнений (0.2) при произвольном T E R+ и n = 3.

• III.    Уравнение Баренблатта - Желтова - Кочиной

(А — A) ut = a Au + f моделирует динамику давления жидкости, фильтрующейся в трещинновато-пористой среде [5]. Здесь а и А - вещественные параметры, характеризующие среду; параметр a E R+- а параметр А может принимать и отрицательные значения, которые не противоречат физическому смыслу задачи [6], функция f = f(x) играет роль внешней нагрузки. Кроме того, это уравнение описывает течение жидкостей второго порядка [7], процесс теплопроводности с «двумя температурами» [8], процесс влагопереноса в почве [9]. Необходимо отметить, что одномерное уравнение Баренблатта - Желтова - Кочиной является одномерным аналогом линеаризованной системы Осколкова [10, 11], описывающей динамику вязкоупругой несжимаемой жидкости Кельвина - Фойгта.

Пусть G = G(V; E) - конечный связный ориоптированный граф. где V = {V)} - множество вершин, a E = {Ej} - множество дуг. Мы предполагаем,что каждая дуга имеет длину lj > 0 и ширину dj > 0. На графе G нас будут интересовать задачи с краевыми uj (0, t) — uk (0, t) — um(lm, t) — un(ln, t), Ej, Ek E Ea(V)), Em, Ek E Eш(V));

(0 . 4)

52 d j U jx (0 ,t ) —

E j E E ^a ( V i ) условиями для уравнений

52    d k U kx ( l k ,t ) = 0;

E k Е Е ^Ш ( V i )

(0 . 5)

λu jt

—

u jxxt    ^au jxx ,

(0 . 6)

описывающих давление жидкости в случае, когда среда представляет собой связный пласт, имеющий слоистую структуру. Здесь через E^{а ( ш} )( V ) ) обозначено множество дуг с началом (концом) в вершине V). Условие (0.4) требует, чтобы все решения были непрерывными на вершинах графа; а (0.5) означает, что поток через каждую вершину должен равняться нулю - аналог условия Кирхгоффа. Если, к примеру, граф состоит из единственной дуги с двумя вершинами, то условия (0.4) отсутствуют, а условия (0.5) превращается в условие Неймана.

В подходящих функциональных пространствах задачи (0.1); (0.2), (0.3); (0.4) - (0.6) редуцируются к линейному уравнению Соболевского типа

Lui = Mu + f.

(0 . 7)

Впервые уравнения, сводящиеся к виду (0.7), появились в работе А. Пуанкаре [12], однако их систематическое изучение началось с работы С.Л. Соболева [13] (см. обстоятельный обзор в [14]).

Целью нашего исследования является разрешимость для уравнения (0.7) так называемой начально-конечной задачи

P j ( u ( T j ) — U j ) = 0 , j = 0 ,n,

(0 . 8)

—то < a < т о < т 1 < т 2 <...< Tn < b <  + то, Pj - относительно спектральные проекторы (которые будут определены позднее). Заметим, что если n = 1, то (0.8) превратится в более простую задачу

P in ( U (0) — U о) = 0 , P fin ( и ( т ) — U t ) = 0 .

(0 . 9)

История задачи (0.7), (0.9) начинается с одной стороны в [15], где она названа задачей Веригина, а с другой стороны и независимо - в [16], где она названа задачей сопряжения. Однако в обоих случаях вместо относительно спектральных проекторов P in и P fin рассматриваются спектральные проекторы оператора L, причем L вдобавок предполагается самосопряженным. Наш подход основан на концепции относительного спектра, предложенной Г.А. Свиридюком [17], и развитой его учениками [18-20], в частности, В.Е. Федоровым. Кроме того, методы, предложенные Г.А. Свиридюком, стали фундаментом алгоритмов численного решения уравнений леонтьевского типа (т.е. конечномерных уравнений Соболевского типа), которые в свою очередь сыграли важную роль в численных исследованиях экономических [21-23] и технических моделей [24, 25].

Первые результаты в этом направлении изложены в [26], где рассмотрен частный случай задачи (0.9) причем с более жесткими чем здесь условиями на L -спектр оператора M. В [27] рассмотрена задача (0.9), но для тех же условий на L -спектр оператора M , что и в [26], однако в этом случае отмечена возможность большего произвола в относительно спектральных условиях.

Необходимо отметить, что в настоящее время начально-конечные задачи для неклассических уравнений математической физики активно изучаются, в том числе и на множествах различной геометрической структуры [28-30]. Заметим еще, что если o fin ( M ) = 0 , то задача (0.9) превращается в задачу Шоуолтера - Сидорова [31] P ( и (0) — и о) = 0 и поэтому считается естественным обобщением последней [32], которая, в свою очередь, обобщает задачу Коши.

Статья кроме вводной части и списка литературы содержит семь параграфов. Первый параграф посвящен исследованию задачи (0.7), (0.9), причем оператор M сильно ( L,p )-радиален [33]. В качестве конкретной интерпретации во втором параграфе статьи показывается однозначная разрешимость начально-конечной задачи (0.9) для системы уравнений (0.1). Частный случай этих результатов был получен в [34]. В-третьем параграфе рассматривается задача (0.7), (0.9) в случае ( L,p )-секториальности оператора M [35]. Данные абстрактные результаты проиллюстрированы конкретным примером, приведенным в четвертом параграфе. Здесь приведена теорема об однозначной разрешимости начально-конечной задачи для системы Навье - Стокса (0.2), (0.3) [36]. В пятом параграфе приводится обобщенная теорема о расщеплении, которая используется в шестом параграфе при доказательстве однозначной разрешимости многоточечной начально-конечной задачи (0.8) для уравнения Соболевского типа с ( L,p )-ограниченным оператором M (0.7) [37]. В последнем, седьмом, параграфе рассматривается начально-конечная задача для уравнений Баренблатта - Желтова- Кочиной на конечном связном ориентированном графе (задача (0.4) - (0.6)), результаты которой опубликованы в [38].

Наконец заметим, что все рассмотрения проводятся в вещественных банаховых пространствах, однако при рассмотрении « спектральных вопросов » вводится их естественная комплексификация. Все контуры ориентированны движением против часовой стрелки и ограничивают области, лежащие слева при таком движении.

1.    Относительно сильно р-радиальный оператор

Пусть Uh F- банаховы пространства, операторы L Е L(U;F) (т.е. линеен и непрерывен) и M Е Cl(U;F) (т.е. линеен, замкнут и плотно определен). Обозначим через pL (M) = {p Е C : (pL — M) -1 Е L(F; U)}

L -резольвептпое множество оператора M. c^L ( M ) = C \ p^L ( M ) - L -спектр оператора M. R L ( M ) = ( pL — M ) ^{- 1} L - правую L -резольвенту оператора M. а через L L ( M ) = L ( pL — M ) ^{- 1} - левую.

Пусть оператор M сильно ( L,p )-радиален (терминология и результаты см. гл. 3 [17]). Известно, что при условии сильной ( L,p )-радиальности существует единица разрешающей полугруппы однородного уравнения (0.2), которая является проектором, расщепляющим пространство U

P = U ⁰ = s- lim U t , t M 0+

U t = . lim ( k < p ±1 R L ( p .„ ( M )) k ⁽ p k →∞ t       _t

Аналогично можно построить проектор для пространства F

Q = F ⁰ = s - lim F t , t M 0+

F t = . lim ( k M1 L L ₍ p .„( M )) k ' p ^+Ц . k →∞ t       _t

Введем в рассмотрение ядра ker U "  = U⁰, ker F "  = F⁰ и об разы im U "  = U¹, im F "  = F¹ этих полугрупп. В силу сильной ( L,p )-радиальности оператора M [39]

U⁰ Ф U¹ = U (F⁰ Ф F¹ = F) .

( A 1)

Обозначим через Lk ^М^ сужение оператора, L (M) iia Uk (domM П Ukk k = 0, 1. II если оператор M силыю (L,p)-раднален. p Е {0}U N. то Lk Е L(Uk;Fk). Mk Е Cl(Uk; Fk). k = 0, 1, причем сущеетвует оператор M—1 Е L(F0;U0). В случае сильной (L,p)-радиальности оператора M, p Е {0} U N выполняется еще одно условие [40] - существует оператор L-1 Е L(F1; U1).

( A 2)

Наконец, введем еще одно важное условие -

L — снектр a^L ( M ) оператора M представим в виде _O ^{L ( M} ) = _CT fin ^{( M} ) ^U _CT ^L n ^{( M} ) , причем a fin ⁽ M ) содержится в ограниченной области D С C с кусочно гладкой границей у, где y П a^L ( M ) = 0.

( A 3)

Построим относительно спектральный проектор

Pfin = 2ni/RL (M) dp, при этом в случае сильной (L,p)-радиальности оператора M справа выполняется PfinP = PPfin = Pfin- Значит, в данном с.туиае сутпествует проектор Pin = P — Pfin. Положим U 1n(fin) = imPin(fin)• F1n(fin) = imQin(fin)' 11 4ePe3 Lin(fin) Min(fin)> обозначим Сужение оператора L (M) на подпространства U 1n(fin) соответственно.

Итак, пусть выполнены условия (А1) - (АЗ), фиксируем т Е R+, и 0, и_т Е U.

Определение 1.2. Вектор-функцию u G C ([0 ,т ];U) О C ¹((0 ,т );U), удовлетворяющую уравнению (0.7), назовем решением начально-конечной задачи (0.1), (0.9), если она удовлетворяет уравнению (0.7), и lim Pin ( u ( t ) — u (0)) = 0, lim Pf_in ( u ( t ) — u ( т )) = 0.

• tm 0+                  tm -

• Имеет место следующая

Теорема 1.1. (Теорема о расщеплении) [17]

Пусть оператор) M сип.оно ( L,p)-радиалсп. Тогда

(У операторы Lin ( fin ) G L (U1 n ₍ fin );F in ₍ fin )). причем сутрствуют операторы L-ffin ) G L ^(F in ( fin ); Uin ( fin ))'

• (и) операторы Min ( fin ) ^G L(Un ₍ fin _}; F ( fin _}).

  Теорема 1.2. (г) семейство {Uf_in

  
  

  : t G R }, fn = U t

  
  

  является

  
  

  однопара

  
  

метрической аналитической разрешающей группой однородного уравнения (0.2) аналити чески продолжимой во всю комплексную плоскости, причем Pfin = Ufin [17, гл. 3];

(in) семейство {U(n : t > 0}. Utn = Ut является однопараметрической разре

^U L eL (U 1 n )

шающей сильно непрерывной полугруппой однородного уравнения (0.2), причем Pin = U0 = s- lim Ut [17. гл. 3].-tm 0+

(ггг) семейство {Rfin : t G R }.

R

t

^fin   2 ni

j ( HL fin

^Г fin

— Mfin ) ¹ e^pdp,

t ∈ R ,

экспоненциально ограничено и аналитически продолжимо во [20, гл. 2];

всю комплексную плоскость

(w) семейство {Rtn G L (F 1_n ; U1_n ) : t >  0 }

Rtn = s- lim k→∞

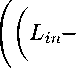
_t        - 1  V⁽ p /         t       - 1

H     Min   Lin      Lin—        Min  ,  ROn = 5- lim R k (p +1)    /     ,             k (p +1)    / in tm 0+ экспоненциально ограничено и сильно непрерывно [20, гл. 2].

М fin ( in ) ^fin ( in )     ^fin ( in )" Rin ( fin )     Lin ( fin ) Qin ( fin ) [•-’•-^,]-

Подействуем на уравнение (0.7) последовательно проекторами I — Q и Qin ( fin ) и сведем его к эквивалентной системе из трех независимых уравнений

Hu ⁰ = u ⁰ + M- ¹ f ⁰ ,                               (1 . 1)

^u in   Sinuin ⁺ Lin fin,                                     ⁽¹ • ²⁾

u⁴ fin   ^S finufin ^{+ L} finffin,                                  ⁽¹ • ³⁾

где H = M- ¹ L 0 G L (U⁰). шльпотептеп степени p G { 0 } U N: Sin ( fin ) = L-n ^ f_in ) Min ( fin ) G ^{L (U} 1n ( fin ))' причем спектр a ⁽ Sin ( fin )) = CT^Ln ( fin )^{( M ); f 0} = ^{(I — Q} ) f- fin ( fin ) = Qin ( fin ) ^f-u ⁰ = ^{(I — P} ) u' uin ( fin ) = Pin ( fin ) ^u-

Теорема 1.3. [33] Пусть оператор M сильно (L,p (-радиален, и часть спектра a fin (M) ограничена. Тогда для любых векторов u 0 ,uT G U и любой век mop-функции f : [0, т ] ^ F. таксиг. что f0 G Cp+1((0pr);F0). fin G C([0,т];F1n)■ ffin G C([0,т];Ff in) ■ cyiiifcrneyern единственное решение u Е C([0,т];U) ПC 1((0,т);U) задачи (0Л), (0.9), которое к тому эюе имеет вид pq                         t                                     τ и (t ) = — ^ Hq M- 1   f 0( t) + UtnU 0 +   RE fin (s) ds + U- Ut -   Rff ( s ) ds. (1.4)

q =0           dt                     ^{0                                 t}

2. Линеаризованная система уравнений фазового поля

Пусть П С R n - ограниченная ос5.таеть с границей д П класса C^ . В пилиидре П х R+ рассмотрим модель Плотникова

9t ( x, t ) + pt ( x, t ) = A 9 ( x, t ) + f ( x, t ) ,

A p ( x, t ) + ap ( x, t ) + в9 ( x, t ) + g ( x, t ) = 0 ,

(2 . 1)

—— ( x,t ) + X9 ( x,t ) = 0 , p( ( x,t )+ Xp ( x,t ) = 0 ,  ( x,t ) Е д П х R+ .        (2 . 2)

∂n                 ∂n

Здесь искомыми функциями являются 9 ( x,t ), p ( x,t ). Редуцируем задачу (2.1), (2.2) к уравнению

LU = Mu + f.

(2 . 3)

Для этого, сначала сделаем замены

9 ( x, t ) + p ( x, t ) = и ( x, t ) , p ( x, t ) = v ( x, t ) .

Тогда система (2.2) примет вид

u_t ( x, t ) = A и ( x, t ) — A v ( x, t ) + f ( x, t ) ,

A v ( x, t ) + ( a — в ) v ( x, t ) + ви ( x, t ) + g ( x, t ) = 0 ,

(2 . 4)

( x, t ) + Xu ( x, t ) = 0 ,   v(- ( x, t ) + Xv ( x, t ) = 0 , ( x, t ) Е д П х R+ .

∂n                  ∂n

Пусть F = U = ( L ₂(П))². Построим операторы

^L (o o) ^{EL (U; F)} , M ( в¹ ( a — в ) I + a) ^EC l ^{(U; F)} ,

причем ker L = { 0 } х L 2(П). a

dom M = { ( u,v ) Е ( H ² (П))² :(—+ X и ( x )=|-—+ X v ( x ) =0 , x Е д П }. ∂n           ∂n

Пусть Aw = A w. dom A = {w Е H ²(П) : | w ( x ) + Xw ( x ) = 0 , x Е д П }.

∂n

тогда

A Е Cl ( L ₂(П)). Через {pk : k Е N } обозначим ортонормированные в смысле скалярного произведения (•, •) в L 2(П) собственные функции оператора A , занумерованные по невозрастанию собственных значений {Xk : k Е N } с учетом их кратности. Тогда L -спектр оператора M имеет вид

a^L ( M ) = ^p_k =

^{( a + X}k ) ^Xk ^{a + X}k ^{— в}

k Е N \{l : Xl = в — a}} .

Понятно, что для такого множества можно подобрать контур у € C, который бы удовлетворял условию (АЗ).

Лемма 2.1. [20] Пусти в - а € ст ( A ). Тогда оnepamop M силино ( L, 0)-радиален.

Построим проекторы

Р in

/

I

Е     ⁽-,T k Wk

Re Ц к E a Ln ( M )

Е   вАмЩик в—а—Хк

Re Ц к E a Ln ( M )

O

O

/

Рр.

fin

/ Е ⁽-,T k Wk

Re Ц к E a LLin ( M ) ^{Е       в}(' ,Ф к ) ф к

W     в—а—Хк

\ Re Ц к E a fin ( M )

O

O

/

и будем искать решение начально-конечной задачи

P in ( и (0) - и о) = 0 ,  P fin ( и ( Т ) - U t ) = 0

(2 . 5)

для системы (2.4). Простоты ради ограничимся случаем f = const и g = const.

Теорема 2.1. Пусти в — а, —а, 0 € ст ( A ), и существ уют такие Хк, и то Re pk € ст fin ( M )• Тогда up и любых и о € dom A, и_т , f, g € L 2(H) существует единственное решение и € C 1([0 ,т ];U) задачи (2.5) для системы (2.4), которое к тому зюе имеет вид

( ^{и (} t ) V v ⁽ t )

ОО Е к =1

( д,Ф к Ф ^в—а—Х к

+

^Е    exp ( а + Х к — в t) ⁽u о , T k Wk

Re Ц к E a Ln ( M )

\

Е

Re Ц к E a Ln ( M )

в exp( O Q t)

^в—а—Х к

(и о , T k Wk

+

/

/

+

I

Е            (а+Хк) Хк expа+Хк—в

Re Ц к Е ст ( _1п ( M )

( t — Т )) ( U t ,T k Wk \

Е

Re Ц к E a fin ( M )

в exp( ( 0^ ( t - т )) ^{в — а—Х} к

(и т ,T k Wk

/

+

/ ^Е Г          7 ^{( а + Х} к ) ^Х к уА] ^{( в—а — Х} к ) П, ^ф к ) ^{— Х} к к^ ф к )     \

W [^{1 exp}^ а + Х к — в t)\         Х к ( а + Х к )         ^Tk

+   ^Re Ц к ^Ea L ⁽ M )

^Е Fl _       ( ^{( а + Х} к ) ^Х к у А] ^{в ( в — а — Х} к ) {^f ,ф k ) ⁺ {^д ,ф к )

Ь [^{1 exp}^ а + Х к — в t)     Х к ( а + Х к )( в — а — Х к )    ^Tk

\ Re Ц к E a L ( M )

( ^Е Г          ^ ^{( а + Х} к ) ^Х к (+ _т-'|А] ^{( в — а—Х} к ) ^кf, Ф k ^ ^{— Х} к<, д,Ф к )     А

W ^{1 exp}^ а + Х к — в ⁽ t  ^Т )Е         Х к ( а + Х к )         ^Tk

^^^^^^^^r

Re Ц к E a LLin ( M )

^Е      Fl _      ( ^{( а + Х} к ) ^Х к        Al ^{в ( в—а — Х} к ) У,Ф к ) ⁺ < д,Ф к )

W      F^{1 exp}^ а + Хк — в ⁽ t ^Т )E Х_к ( а + Х_к )( в — а — Х_к ) ^Tk

\ Re Ц k E a L _i n ( M )^{L         4}

3.    Относительно р-секториальный оператор

Пусть U и F - банаховы пространства, операторы L € L (U; F) (т.е. линеен и непрерывен) и M € Cl (U;F) (т.е. линеен, замкнут и плотнс) определен), причем оператор M ( L,p )-секториален, p € { 0 } U N (терминология и результаты см. гл. 3 [17]). Рассмотрим линейное однородное уравнение Соболевского типа

Lie = Mu.

(3 . 1)

Тогда существуют вырожденные аналитические полугруппы операторов

U t =     [ R^L L ( M ) e ^ d^ и F t = -^ [ L^L L ( M ) e ^ dp,

2ni Jy                        2ni Jy определенные на пространствах U и F соответственно. Введем в рассмотрение ядра ker U" = U0, ker F • = F0 и об разы imU " = U1, imF " = F1 этих полугрупп. Нетрудно показать, что U0 ф U1 = U0 ф U1 = U0 ф U1, F0 ф F1 = F0 ф F1 = F0 ф F1. Нам потребуется более сильное утверждение

U⁰ ф U¹ = U (F⁰ ф F¹ = F) ,

( B 1)

которое имеет место либо в случае сильной ( L,p )-секториальности оператора M справа

(слева), p G {0}UN. либо реф.текспвпсэсти пространства U (F) [40]. Обозыачим через Lk Mik) сужение оператора, L (M) iia Uk (domM ПUk). k = 0, 1. II если (зператор M силыю (L,p)- секториален справа и слева, p G {0}UN, то Lk G L(Uk;Fk), Mk G Cl(Uk;Fk), k = 0, 1, причем

существует оператор M 0 ¹

G L(F0;U0). а также проектор P = s — lim Ut Q = s — lim Ft. tM 0+            tM 0+ расщепляющий пространство U (F) согласно (Bl), причем U1 = imP (F1 = imQ). Введем еще одно условие - существует оператор L-1 G L(F1; U1),

( B 2)

которое имеет место в случае сильной ( L,p )-секториальности оператора M, p G { 0 } U N. (Кстати, в [39] показано, что (В1) вместе с условием ( L,p )-секториальности оператора M, p G { 0 } U N. дает ciпьнуто ( L,p )-секторналыю(?ть оператора M справа, (слева), p G { 0 } U N. а если к ним добавить условие (В2), то получим сильную ( L,p )-секториальность оператора M.p G{ 0 }U N).

Наконец, введем еще одно важное условие -

L — сиектр o^L ( M ) оператора M представим в виде ^ L ^{( M} ) = f ⁽ M ) ^U a L ⁽ M ) , причем o f in ⁽ M ) содержится в ограниченной области D С C с кусочно гладкой границей Y, причем y П o L ( M ) = 0.

( B 3)

Построим относительно спектральный проектор [35]

Pfin = 2ni/Rf (M) d^, причем оказывается, что при условии сильной (L,p)-секториальности оператора M справа PfinP = PPfin = Pfin- Значит, в данном случае существует проектор Pin = P — Pfin-Итак, пусть выполнены условия (Bl) - (ВЗ), фиксируем т G R+, и0, uT G U, и для уравнения (3.1) рассмотрим начально-конечную задачу: найти вектор-функцию v G го(R+;U), удовлетворяющую уравнению (3.1) и условиям

P in ( и (0) — и 0) = 0 , P fin ( и ( т ) — и т ) = 0 .                         (3 . 2)

Тогда существует аналитическая группа {U fin : t G R } , где

^U t = 1- [ R^{f ( M} ) e ^t d^,  U fin =     [ R^{f (} M ) e ^t d^

2ni yr ^                 f      2ni Y-v такие, что s -

^R+ }. г.те U n

— lim U t = P h U ° = P fin. Построим аналитическую полугруппу t M 0+              fin

, = U t — U fin- ОчевИццо, s — _fHm U tn = P in" По.кзжим im P in ( f _in ) ^:

-

^{Ui n ^: t ^G

^U in ( fin )•

очевидно, U¹ = U1_n фU fin. Справедлива

Теорема 3.1. Пустъ оператор M ( L,p)-секторпален, p G { 0 }U N, n выполнены условия

(Bl) - (ВЗ). Тогда при любых т G R+, и 0, и_т G U существует единственное решение задачи (3.1), (3.2), которое к тому снсе имеет вид и ( t ) = Ui^n⁴ 0 + Uff-nи_т-

Тот факт, что вектор-функция и(t) = Utnuо + Uft-nиТ удовлетворяет уравнению (3.1), проверяется непосредственно. Выполнение условия (3.2) следует из соотношений PinUfin = O 11 PfinUin = O а Ttжже Uin = PinUin = UtnPin 11 Ufin = PfinUfin = UfinPfin nDn BCex t Е R+ в случае Utn и при всех t Е R в случае Ufin- Единственность решения вытекает из эквивалентности уравнения (3.1) системе уравнений u0 = 0, u 1n = Sin un, ufin = Sfinu1 in, где Sin = LinMin E Cl(U1n;F 1n) - секторпалыили оператор. Sfin = L—nMfin E L(U1in;F1in): подпространства F 1n и Ffin строятся аналогия но пространствам U1n и Ufin, только вместо полугруппы {Ut : t Е R+} и группы {Ufin : t Е R} надо взять полугруппу {Ft : t Е R+} и группу {Ffin : t Е R}, где, соответственно,

F t =      [ L L ( M)e ^ dp, F fin =      [ L L ( M ) e ^t dp ;

2 ni г                   J      2 ni y операторы Lin(fin) Min(fin)) есть сужеииe операторов L1 (M1) iia U 1n(fin) (domM П U1n (fin)-

4.    Уравнение Навье - Стокса

Пусть И с R ⁿ. n = N \{ 1 }. - ограниченная об.тасть с границей д И кла.сса C^. В цилиндре И х R₊ рассмотрим задачу Дирихле

v(x, t) = 0,   (x, t) Е дИ х R+ для системы уравнений Навье - Стокса vt = vV2v — Vp,  V • v = 0.

(4 . 1)

(4 . 2)

Прежде чем редуцировать систему (4.1) к уравнению (3.1), представим ее в виде vt = vV2v — p,  V (V • v) = 0.

Система (4.2) получена из (4.1) после замены Vp ^ p [41].

Для редукции уравнений (4.2) к уравнению (3.1) нам потребуются функциональные пространства из [42]. Пусть H ² и H ² (H _ст и H ^ ) - подпространства соленоидальных и потен-циальпых вектор-<]>упкп1п1 пространства. H² = ( ^ ₂²(И) П W 2(И)) ⁿ (L² = ( L ²(И)) ⁿ ). Формулой A = diag {V ² ,..., V ² } задается линейный непрерывный оператор с дискретным конечнократным отрицательным спектром а ( A ), сгущающимся лишь на —то . Обозначим через А_а ( _п ) сужение оператора A нa H ² ( _п ).

Лемма 4.1. (теорема Солонникова - Воровича - Юдовича). Оператор А_а ( _п ) Е L (H ² ( _п ) , H а ( п ))• ГФ'¹-^^м а ( Ay -( п )) = а ( A ) 11 A = A_CT E + An П.

Здесь через П Е L (H² , H) обо'значеи проектор вдоль H ² . E = I — П.

Лемма 4.2 (теорема Капитанского - Пилецкаса). Формулой B : u ^ V ( V • и ) задается onciximop B Е L (H² , H _п ). причем ker B = H ².

Положим U = F = H у- х H _п х H _р . H _p = H _п. Beiстор и Е U имев'т вид и = ( и_а,и_п,u_p ). Формулами

/ I O O \         / vA ct O O \

L = O I O   , M = O vA_n — I

OOO      O B O задаются операторы L Е L (U; F). im L = H a х H П х {0}. ker L = {0} х {0} х Hpii M Е Cl (U; F).

dom M = H х Н П х H p. Итак, редукция уравнений (4.2) к уравнению (3.1) закончена.

Лемма 4.3. [43]. При любых v Е R+ оператор M силъно ( L, 1)-секториален.

Построим подпространства U⁰ = F⁰ = { 0 } х Н _П х Н p , U¹ = F = Н _a х { 0 } х { 0 }.

Выполнение условий (В1) и (В2) очевидно, причем

M 0

O

O

O

O

O

O

O

O

O

где В_П - сужение оператора B на Н П (из леммы 2 вытекает, что В_П : Н П ^ Н _П - топлинейный изоморфизм). Нетрудно также проверить, что

M^{- 1} L о =

OO

OO

OO

- 1

O

O

-

нильпотентный оператор степени 1.

Спектр ст ( A ) = {Х к } , г де Х к Е R — - собственные значения, занумерованные по невозрастанию с учетом их кратности, тогда ct^l ( M ) = {v- ¹ Х к } . Понятно, что для такого множества можно подобрать контур у Е C, который бы удовлетворял условию (ВЗ).

Теперь построим

t

U in ( fin )

Е v 1 ХкEaL in(fin)

e^vXk4-,W Wk O

V

( M )

O

O

O

O

O

O

O

Тогда в силу теоремы 3.1 и леммы 4.3 справедлива следующая

Теорема 4.1. [36] При любых v Е R+, и о ,иТ Е U существует единственное решение задачи (3.2) для системы уравнений (4-2), причем это решение и = и(t) имеет вид ua (t) — U1 ита + U2и0a, ип = 0, up = 0 *

5.    Обобщенная теорема о расщеплении

Пусть U и F — банаховы пространства, операторы L Е L(U; F) (т.е. линеен и непрерывен) и M Е Cl(U;F) (т.е. линеен, замкнут и плотно определен). Пусть относительный спектр оператора M ctl (M) = стL (M) U CTL (M). причем ctl (M) = 0, существует замкнутый контур Г С C, ограничивающий область D D стL (M), такой, что D П стL(M) = 0*

(5 * 1)

(5 * 2)

Построим интегралы типа Ф. Рисса (понимаемые в смысле Римана)

P=2^1 R L ⁽ M ) d^- г

Q = -¹, [ L^L L ( M ) dp, 2 пг      ^

г где RL(M) (LL(M)) - права!i (левая) L-резольвенты оператора M.

Лемма 5.1. Пусть a^L ( M ) = aL ( M ) Ua^L ( M ), причем выполнено (5.1). Тогда, операторы P : U ^ U г I Q : F ^ F - проекторы.

Положим U⁰(F⁰) = ker P (ker Q ). U¹ (F¹) = im P (im Q ) ii нерез Lk MkC обозначим сужение оператора L (M ) iia U^k (dom M О U^k). k = 0. 1.

Теорема 5.1. Пусть выполнены условия леммы 5.1. Тогда

• (г) Lk ЕС (U ^k ;F ^k ). k = 0.1:

• (и) Mo Е Cl (U⁰;F⁰). M i Е С (U¹; F¹).:

(Hi) существуют операторы L— ¹ Е С (F¹;U¹) и M— ¹ Е С (F⁰;U⁰).

Как известно, оба этих утверждения первым сформулировал и доказал Г.А. Свиридюк, правда, при более ограничительном условии, а именно:

aL ( M ) = 0, существует замкнутый контур Г С C , ограничивающий область D D aL ( M ) .

}

(5 . 3)

Однако внимательный анализ его доказательств (см. [17], лемма 4.1.1 и теорема 4.1.1) показывает, что они годятся и в нашем случае.

Пусть aL (M) = (J aL (M), n Е N, причем aL (M) = 0, j=o существует замкнутый контур Гj С C, ограничивающий область Dj D aL(M), такой, что Dj ^ aL(M) = 0 и Dk П Di = 0 при всех j, k,l = 1 ,n,k = l.

• (5 . 4)

• (5 . 5)

Аналогично (5.2) построим интегралы

Pj = -1, [ R^LL ( M ) dp, Qj = -^ [ LL ( M ) dp, j = 1 ,n.

• ^{2 n}i г j                       ^{2 n}i г j

Лемма 5.3. [37] Пусть выполнены условия (5.3), (5-4). Тогда операторы

(i.) Pj : U ^ U t1 Qj : F ^ F - npoetсторы. j = 1 , n:

• (n) PkPl = O. QkQl = O. Ы = Tn.k = l.

nn

(Hi) P o = P — У^ Pj 'ii Q o = Q — Qj - проекторы.

j =1                  j =1

(Заметим, что здесь ради экономии места проекторы Pj и Qj, j = 1 , n, из (5.5), а проекторы P и Q из (5.2), но с заменой условия (5.1) на условие (5.3)).

Положим U⁰(F⁰) = ker P (ker Q ). U 1 (F1) = im Pj (im Qj ). j = 0 ,n. ii через L o ( M o) обозначим сужение оператора L (M ) нa U⁰ (dom M П U⁰), а через L ₁ j M1 ₁ j ) обозначим сужение оператора L (M ) iia U 1 (dom M П U 1). j = 0 , n.

Теорема 5.1. (Обобщенная теорема о расщеплении) [37] Пусть выполнены условия (1.3), (1.4). Тогда

'(г) L o Е С (U⁰;F⁰). L 1 j Е С(Uj ;F j ¹). j = 0 7n_

• (и) Mo Е Cl(U⁰;F⁰). M1 j Е С(Uj;Fj¹ )■ j = 0,n ___

6.    Относительно ^-ограниченные операторы

(Hi) существуют операторы L—j Е С (F1; U 1), j = 0 ,n, и M— ¹ Е С (F⁰;U⁰).

Пусть U и F _ банаховы пространства, операторы L Е С(U; F) (т-е. линеен и непрерывен) ii M Е Cl(U;F) (т.е. линеен, замкнут и плотисt определен), причем оператор M (L,p)-ограничен, p Е {0} U N (терминология и результаты см. гл. 5 [17]). Рассмотрим линейное уравнение Соболевского типа

Lui = Mu.                                      (6 . 1)

Решением u = u ( t ) уравнения (6.1) назовем вектор-функцию u Е ^ (R; U), удовлетворяющую этому уравнению.

Определение 6.1. [17] Отображение U^. Е C^ (R; L (U)) назовем группой разрешающих операторов уравнения (2.1), если

(!) иt u s = и t ⁺ s при всех s. t Е R:

• (ii)    при всех v Е U вектор-функция u = U t v есть решение уравнения (2.1).

В дальнейшем, следуя традиции, будем отождествлять группу разрешающих операторов уравнения (6.1) с ее графиком {Ut : t Е R }, и в дальнейшем называть просто группой уравнения (6.1). Группу {Ut : t Е R } уравнения (6.1) будем называть аналитической, если она аналитически продолжима во вето комплексную плоскость с сохранением свойства (i).

Теорема 6.1. Пусть выполнены условия (5.3), (5.4). Тогда существуют аналитические группы уравнения (6.1)

U t =     [ R L ( M ) e^dp, U t = 1- [ R L ( M ) e^dp-J = 1П

• 2 ni ^p                 j 2 ni ^p

г                               r j причем

• (i)    UtUss = UssUt = Ut ^{+ s} при всех s. t Е R. j = Т П

• (ii)    U k U ss = U ss U k = O при всех s. t Е R. k. l = 1 , n. k = l.

n

(Hi) U0 = Ut — У Uj - аналитическая группа уравнения (6.1).

j =1

Далее возьмем вектор-функцию f Е C ^ (( a,b );F) и рассмотрим линейное неоднородое уравнение Соболевского типа

Lui = Mu + f.                                  (6 . 2)

Вектор-функцию u Е C^ (( a,b );U), удовлетворяющую уравнению (6.2), назовем решением уравнения (6.2). Решение u = u ( t ), t Е ( a,b ) уравнения (6.2), удовлетворяющее условиям

P j ( u ( T j ) — u j ) = 0 , j = 0 , n,                                 (6 . 3)

назовем решением многоточечной начально-конечной задачи для уравнения (6.2).

Теорема 6.1. [37] Пусти оператор M (L,p'(-ограничен, причем выполнено условие (5.4). Тогда для любых f Е C^((a,b);F)), uj Е U, j = 0,n существует единственное решение задачи (6.2), (6.3), которое к тому снсе имеет вид p                                       n               nt

u ( t ) = — £( M - ¹ L о) q M - 1(I — Q ) f ⁽ q )( t ) + ^U — u j +     / U jt-s L -j¹ Q j f ( s ) ds.

q =0                             j =0           j =0 j

7.    Уравнение Баренблатта - Желтова - Кочиной на графе

Пусть G = G(V; E) - конечный связный ориентнрованный гра<]>. где V = {Р)} - множество вершин, a E = {Ej} - множество дуг. Мы предполагаем,что каждая дуга имеет длину lj > 0 и ширину dj > 0. На графе G нас будут интересовать задачи с краевыми uj (0, t) — uk (0, t) — um(lm, t) — un(ln, t), Ej, Ek Е Eа(V)),Em,Ek Е Еш(V));

(7 . 1)

52 d j u jx (0 ,t ) -

E j e E ^a ( V i ) условиями для уравнений

52    d k U kx ( l k ,t ) — 0;

E k Е Е ^Ш ( V i )

(7 • 2)

λu jt

^^^^^^^^.

u jxxt    ^au jxx .

(7 . 3)

Введем множество

L2(G) — {g — (g i ,g 2, •••,gj,...) : gj € L 2(0, lj)}, которое становится гильбертовым пространством со скалярным произведением lj

(g, h) ^— ^ d j j g j ( x ) h j ( x ) dx.

E j e E 0

Перез U обозначим множество

U — {u — ( и 1 , u ₂ ,... ,U j ,... ) : U j € W 21(0 ,l j ) , 11 выполз вено (7.2) }.

Множество U является гильбертовым пространством со скалярным призведением и нормой lj                                                                                        lj

[ u, v ] — 52 d j / ( U jx V jx ( x ) + U j V jx ( x )) dx,   I N I и — 52 d j / ( u 2 x ( x ) + U 2( x )) dx.

E j ^e E   0                                            E j ^e E   0

В силу теорем вложения Соболева пространство ^ }(0 ,l j ) состоит из абсолютно непрерывных функций, а, значит, пространство U корректно определено, плотно и компактно вложено в L2(G). Отожд ествим L2(G) со своим сопряженным и через F обозначим сопряженное относительно двойственности (•, •) пространство к U. Очевидно, F - банахово пространство, причем вложение U ^ F компактно.

Формулой lj

(Au,v) — ^ d j /( U jx ( x ) V jx ( x )+ au j ( x ) V j ( x )) dx,

E j e E 0

где a € R+ , u,v € U. зададим оператор, определенный на пространстве U. Поскольку

|(Au,v)| < Ci||unиH^hи в силу неравенства Коши - Буняковского и

C 2|| ^u||и < ⁽A^u,u)< C з ^|u|U

(7 . 4)

при всех u,v € U и иекоторых Ck € R+- к — 1, 2, 3. то лииейиьи! оператор A : U ^ F непрерывен и инъективен. Кроме того, из первой оценки (7.4) вытекает сюръективность сопряженного оператора A* : F* ^ U*. В силу рефлексивности пространства U и самосопряженности оператора A получаем, что оператор A € L(U; F) биективен. Отсюда по теореме Банаха следует существование оператора A-1 € L(F;U). Поскольку вложение U ^ F компактно, то оператор A-1 € L(F) является компактным. 3начит, спектр оператора A вещественен, дискретен, конечнократен и сгущается только к + то.

Теперь фиксируем а € R+ и А € R и построим операторы

L — ( А - a )I + A, M — а ( a I - A ) .

Из сказанного следует

Теорема 7.1. (см. наир. [44]). Операторы L,M Е L (U; F), причем спектр ст ( L ) оператора L вещественен. дискретен, коней)юкратен и сгущается только к —го.

Из теоремы 7.1 вытекает, что оператор L -фредгольмов, причем ker L = { 0 }, если 0 / ^{ст (} L )•

Лемма 7.1. (см. наир. [44]). Пусть параметры a,X Е R \{ 0 }, тогда оператор M ( L, 0)- ограничен.

Пусть {Xk} - собственные значения оператора A, занумерованные по неубыванию с учетом их кратности; a {vk} - соответствующие им ортонормированные в смысле L 2(G) функции. По формулам (5.2) построим проекторы

P ={

I , ес ли 0 / ст ( L );

I — Е (•, V k Wk, ^ес-¹¹¹ 0 Е ст ( L );

X k = X - a

Q = I

I , если 0 / ст ( L );

X k = X - a

(заметим, что несмотря на "похожесть" проекторы определены на разных пространствах) и разрешающую группу

ОО

Ut = ^wk^ ,vk V, k=1

где штрих у знака суммы означает отсутствие членов ряда с номерами k такими, что X k =

X — a: (•, • )-скаляриое пуюизведеыие в L2(G). L-спектр оператора M имеет вид стL (M) = {^k = а(a  Xk) , k Е N}.

X — ( a + X k )

Выполнение условия (5.3) очевидно, выберем ст ^ ( M ), j = 0 , п , так, чтобы выполнялось условие (5.4) (понятно, что это можно сделать не одним способом). Построим проекторы

Pj =    52    k^,Vk Wk ,j = 0 ,n.                         (7 . 5)

-kC^L ( M )

Возьмем — го < a < т о < т 1 < т ₂ < ... < Tn < b <  + го. и, E U. j = 0 ,n. f E C^ (( a,b );F) 11 рассмотрим задачу (6.2), (6.3), где U- функциональное банахово пространство с краевым условием (7.1), операторы L и M из (6.2), а проекторы Pj, j = 0 , п , из (6.3).

В силу леммы 7.1 и теоремы 6.1 вытекает

Теорема 7.2. При любых X Е R, а Е R \{0} и, Е U, j = 0,п, многоточечная начальноконечная задача (6.3), (1.1), (1-3) для уравнений (1.3) имеет единственное решение и Е C^((a,b);U), которое к тому енсе имеет вид и (t ) = ]Т £   e-k(-Т.) (u, ,vk )vk.

^j =⁰ - k C ^ L ( M )

Автор выраснсает свою искреннюю признательность профессору Г.А. Свиридюку за постановку задачи и интерес к работе, а так снсе М.А. Сагадеевой за плодотворные дискуссии.