Национальные особенности изменения опасности развития пандемии коронавируса COVID-19: математическое моделирование и статистический анализ

ннотация.

Исключительные события, связанные с распространением инфекции корона вируса COVID-19 среди населения различных стран, предоставляют информацию для сравнительного анализа и количественной оценки качества принимаемых решений в различных национальных обстоятельствах борьбы с пандемией. С использованием математических моделей теории надежности выявляется общая тенденция изменения эпидемических кривых и проводится оперативный расчет коэффициентов моделей и динамики численности установленных случаев заболеваний по функции отказов (фактов заражений), плотности вероятности отказов (роста доли инфицированных), интегрированной опасности и риска заражения, приемлемого риска, первичной готовности к эпидемии и управляемости текущей эпидемической ситуацией. Россия, в отличие от других стран, вступила в эпидемический процесс с высокой готовностью — малым показателем приемлемого риска, но продемонстрировала низкую управляемость текущей ситуацией. Функции надежности основаны на двойной интерпретации уравнения изменения меры опасности во времени и по факторам развития эпидемического процесса, в частности, по возрасту населения. Базовым для математического и статистического анализа является экспоненциальное уравнение опасности, которое в полулогарифмической шкале представлено линейной зависимостью от времени. Ее искажения за счет варьирования управляемой величины приемлемого риска указывает на национальные особенности регулирования эпидемической нагрузки на население. Все показатели надежности имеют ясный смысл и взаимосвязаны. Для прогнозирования необходимо знать моменты начала и пика эпидемии, потенциал заражения в группе риска, приемлемый риск. По данным в фазе экспоненциального роста приемлемый риск линейно снижается со временем до минимального значения, что становится основанием для оценки управляемости эпидемической ситуацией и дальнейшего совершенствования модели.

лючевые слова:

пандемия СОVID-19, страновые особенности эпидемических кривых, ма тематические модели опасности заражения, показатель предварительной готовности, управляемость ситуацией.

Текущие события, связанные с распространением инфекции COVID-19 (SARS-CoV-2), поставили перед глобальным сообществом много новых биомедицинских, хозяйственных, демографических и иных проблем. Ситуация в различных странах быстро меняется в зависимости от особенностей географического положения, культурно-исторических традиций населения и типа национальной организации государственного управления здравоохранением, в соответствии с которыми изменяются характеристики эпидемического процесса и вырабатывается местная тактика и стратегия борьбы с эпидемией, ставшей пандемией. Осуществляется беспрецедентный глобальный мониторинг этого процесса с детальной фиксацией многочисленных статистических показателей по странам, регионам, отдельным районам и городам с разверткой во времени и по возрасту. Такая информация поступает в реальном времени, служит для принятия оперативных решений, позволяет ученым проверить гипотезы, выявить новые закономерности, построить модели и проверить их эффективность.

Предсказание возникновения пандемии — занятие неблагодарное, но готовиться к ней необходимо заранее [1]. В октябре 2019 г. Университет Джона Хопкинса и журнал «The Economist» опубликовали рейтинг безопасности стран с точки зрения их устойчивости к воздействию эпидемий [2], в котором на первых местах находились США и Великобритания. В общемировом и всероссийском масштабах цели санитарно-эпидемиологической

безопасности служит развитие системы здравоохранения, что снижает риски воздействия ведущих причин нездоровья и смертности на индивидуальном или популяционном уровне [3]. Популяционное здоровье и первичная заболеваемость населения зависит от многих факторов — генетических, природно-климатических, социально-экономических, учет которых необходим для решения социально-демографических проблем, повышения качества жизни и развития страны и её регионов [4]. Пандемия COVID-19 еще раз выявила территориальный, национальный, этнический и расовый характер глобальной вирусной эпидемии [5].

Для объяснения закономерностей распространения нового коронавируса были предложены различные математические модели процесса [6]. При этом отмечалось, что из-за ограниченности доступной информации на предварительном этапе используются упрощенные модели, не учитывающие неоднородность популяции, но по мере развертывания процесса качество моделей и основанные на них рекомендации совершенствуются [7]. По мере поступления информации начинают использовать классическую и обобщенную динамическую модель SIR [8; 9]. Отмечается, что расчетные коэффициенты модели сходны по регионам, но в разные периоды наблюдений отличаются, изменяются со временем, что связывается с эффектом регулирования ситуации — усилением мер профилактики и борьбы с эпидемией [10].

Для описания механизма эпидемического процесса используется логистическое уравнение модели SIR [9]:

as         ат

а) — = -aIS , б) — = aIS = aI(S-I) , dt              dt             ⁰

где S 0 и S ( t ) —исходное, базовое в группе риска и текущее количество не болевшего населения, восприимчивого к инфекции (тыс. человек) в момент t —(потенциал заражения); I ( t ) —число подтвержденных случаев заболевания с начала процесса t = t ₀

(в днях); а — положительная константа (частота контактов в расчете на тыс. человек, 1Дыс. чел х день). Эти уравнения использовались как основа для оценки опасности распространения гриппа птиц, прогноза риска возникновения эпизоотий и эпидемий [11] с учетом возрастного состава и миграции населения [12] в неоднородной географической среде.

В начале процесса, когда S » S 0 , нарастание I ( t ) идет по экспоненте

I (t) = exp [aS0 (t -10)]

или в полулогарифмическом масштабе

ln I(t ) = aSо I(t - t0 ) — по прямой зависимости от времени t . Очевидно, что в фазе экспоненциального роста необходимо снижать частоту контактов a и размер группы риска S0, что достигается территориальной и личной изоляцией (разобщением) населения, соблюдением гигиенических требований, вакцинацией и в целом наличием коллективного иммунитета.

На размножение вируса COVID-19 в человеческой популяции влияет множество факторов. Процесс разворачивается во времени и пространстве, имеет свои возрастные и региональные особенности, поэтому трудно создать универсальную модель, учитывающую множество показателей и коэффициентов их связей, подлежащие статистической оценке, чтобы получить точные результаты описания эпидемических систем. Необходимы разные модели, полисистемный подход [13], когда для решения поставленной проблемы используются наиболее удобные, простые и адекватные соотношения. Одним из перспективных направлений моделирования является оценка опасности и риска [14–16], в данном случае — риска распространения коронавируса среди населения разных регионов и стран, для разработки стратегии обеспечения безопасности. Показателем

такой оценки служит демографическая реакция на изменение ситуации вследствие естественных причин и действия органов государственной власти [17].

При знакомстве с эпидемическими кривыми COVID-19 [18] обращает на себя внимание, что быстрое развертывание процесса соответствует странам и регионам в основном с высокими уровнем и качеством жизни. По числу установленных на 17 апреля 2020 г. случаев заболевания — это США, Испания, Италия, Германия и Франция, в Италии — Милан (Ломбардия), в США — Нью-Йорк, в России — Москва. Особенностью эпидемических кривых опасности в полулогарифмической шкале является линейный рост в начале процесса и выпо-лаживание в конце (рис. 1).

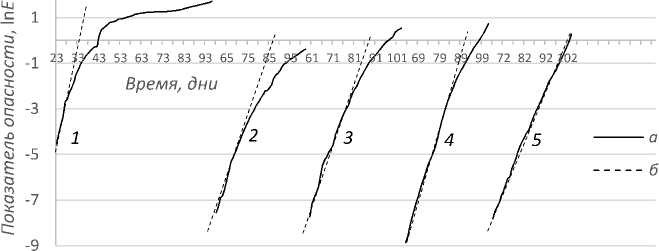
Рис. 1. Изменение опасности ln E(t) развития эпидемии коронавируса CAVID-19 в разных странах: 1 — Китай, 2 — Франция, 3 — Германия, 4 — США, 5 — Россия.

Условные обозначения: а — эпидемические кривые ln E(t) , б — линейная аппроксимация этих кривых в первой фазе процесса — 102 дня 2020 года

Fig. 1. Changes in the hazard index In E(t) of the COVID-19 coronavirus epidemic process in different countries: 1 — China, 2 — France, 3 — Germany, 4 — USA, 5 — Russia. Symbols: a — epidemic curves In E(t) , б -linear approximation of these curves in the first phase of the process -102 days in 2020.

Источник: Пандемия COVID-19. Материалы Википедии. [Электронный ресурс] — Режим доступа: (дата обращения: 17.04.2020).

Время начала процесса, показатели скорости роста, пик заболеваемости и стационарный уровень индивидуальны для населения разных территорий. Эти закономерности здесь формализуются в терминах теории надежности, применяемых в популяционной динамике [19], в том числе для исследования качества жизни [15; 20].

По определению надежность — свойство объекта сохранять во времени в установленных пределах значения всех параметров, обеспечивающих выполнение своих функции в данных условиях [21; 22]. Надёжность связывается с отсутствием отказов (утрат, потерь, жертв, аварий) в работе (деятельности) — свойством объекта сохранять его работоспособность (жизнедеятельность) во времени или в процессе наработки по принятому параметру (возрасту, расстоянию, числу применений). Отказ в эпидемическом процессе связан со случаями инфицирования, потерей здоровья или смертью человека. Надежность характеризует ситуацию без

учета числа объектов в системе, в их ожидаемом осредненном поведении.

Для количественной оценки развития эпидемии используют показатели надежности, например, вероятность безотказной работы до момента t (в днях с начала пандемии, 31 декабря 2019 г. для COVID-19), которая задается убывающей функцией надежности P * ( t ) типа вероятности сохранения здоровья к моменту t . Функция кумулятивной вероятности накопления отказов (ненадежности) равна F * ( t ) = 1 — P * ( t ) так что в эпидемиологической модели (1): S ( t ) = S 0 P * ( t ) , I ( t ) = S 0 F * ( t ) В силу относительности показателей надежности P * ( t ) = S ( t ) / S о , F * ( t ) = I ( t ) / S o на их величину мало влияет принятая в стране методика статистического учета случаев инфицирования, что определяет преимущества аналитических вычислений по формулам надежности.

На основе функции надежности P * ( t ) рассчитываются другие показатели:

P   =- dF^ , E ( t ) = - in p * ( t ) , p ( t ) = dE = . P i t ) ,           (2)

⁽ ) dt                                ⁽ ) dt    P * ( t )

где P ( t ) — функция плотности вероятности (распределения) отказов, в частности, доля подтвержденных случаев инфицирования за единицу времени; E ( t ) — интегрированная опасность, вероятность того, что процесс будет развертываться до момента t ; G ( t ) = 1 - E ( t ) — мера возможности достижения состояния безопасности; p ( t ) —интенсивность отказов,дифференцированная опасность,или риск, равный доле заболевших за единицу времени в численности чувствительного населения S ( t ) (заболеваемость).

Для описания эпидемического процесса удобно принять экспоненциальную функцию опасности, распространенную в биосоциальных, финансово-экономических и страховых приложениях:

E (t )=—In P * (t )= exp( k ( t — tm )) ,(3)

где k —положительный постоянный коэффициент (приемлемый риск— ПР); t_m — момент максимального развития (пика) процесса. Тогда P * ( t ) соответствует дважды экспоненциальной функции вероятности Гомпертца [19]:

P* (t) = exp[—exp(k(t — tm))],(4)

P (t) = ePm exp (k (t — tm )) exp [— exp ( k (t — tm ))] ,(5)

P (t ) = dEt) = k exp( k (t — tm)),(6)

где P(tm) = Pm —максимальное значение P(t) (на пике развития эпидемии).Урав- нение (6) для интенсивностей отказов p(t) соответствует известной модели Кокса, применяемой при изучении зависимости риска наступления события от продолжительности пребывания объекта в группе риска [14]. Приемлемый риск (ПР) p(tm) — k определяет границы безопасности G(tm) = 0 существования рассматриваемой системы, достигаемые при t — tm. ПН — это уровень риска, с которым общество готово мириться, в данном случае на общегосударственном уровне в конкретных обстоятельствах пандемии.

Функция опасности (3) удовлетворяет дифференциальному уравнению

dE — kE (t) dt

Такая модель обеспечивает экспоненциальный рост числа установленных случаев инфицирования населения в первой фазе эпидемии:

F * (t ) = 1-P * (t ) — 1-exp(-exp [ k (t - tm)])»1-{1-exp [ k (t - tm )]} — exp [ k (t - tm)] (8)

Следовательно, показатель ПР

k —-aAtn-1)Sn /At +1/At , At — t -t , Nt =t -N (9) 0        0 х m ' m , m m 0 , m lm 0

а при малых k будет F * ( t ) » 1 -exp { -[ 1 + k ( t - t m ) ^] } — функция эпидемической ситуации, реализованной в Китае.

моноэкспоненциальная

В эпидемическом процессе на первых этапах наблюдается только значение I ( t ) — S 0 F * ( t ) — S 0 [ 1 - P * ( t ) , причем величина потенциала заражения S 0 неизвестна. Для определения коэффициентов перечисленных уравнений теории надежности по данным необходимо рассчитать величину опасности в логарифмическом масштабе по формуле:

ln ^{E (} t ^{) — ln} { ^{- l}n [ ( ^S 0 ^- I ⁽ t ) ) / ^S 0 ] } = ^k ( t ^- t m ) (10) Подбираем значение S 0 так, чтобы обеспечить линейную зависимость ln E ( t ) от t (см. рис. 1).

Возможна общая постановка задачи исследования факторной зависимости опасности E ( t , x,у ) — гладкой функция времени t и показателей наработки (жизнедеятельности) x и y , характеризующей, например, возраст системы x или иной показатель y ее динамического состояния. Эту функцию можно рассматривать как поверхность многообразия связи переменных E [ t , x ( t ) , у ( t ) ] , касательная к которой в точке ( x , у ) описывает процессы уравнением полного дифференциала этой функции E [ t , x ( t ) , у ( t ) ] по параметру направления изменения t (производная Лагранжа):

dE Э E Э E Э E ---—--+ n--+ n --- dt Эt x Эx у Эу

где nx — dx/dt ny — dy/dt —скорости изменения состояния системы по характеристикам. В случае dE / dt — p(t) — 0 уравнение (11) описывает непрерывный замкнутый поток элементов без потерь (безрисковый процесс). От вида функции по- терь зависит решение уравнения (11), в частности, в варианте дифференциальной связи (7), которая описывает изменение функции только от параметра t. Сопостав- ление (7) и (11) дает дифференциальное уравнение зависимости опасности также от факторных переменных (x,у):

Э E Э E Э E --+n--+n -- kE (t, x, у).

Э t    x Э x   у Эу

Уравнения такого вида в популяционной динамике называются уравнениями Мак-

Кендрика— Фон Фестера [8, 20]. Оно имеет фундаментальное значение и применимо к любой аналитической функции E ( t , x,у ) , что используется при моделировании. Важно подчеркнуть эквивалентность двух способов описания (7) и (12): первый удобен для анализа временных рядов данных, второй— при учете факторного влияния. Находятся первые интегралы дифференциального уравнения (12) — функции, которые сохраняют постоянное значение вдоль любого его решения, являющегося функциональной комбинацией Ф ( C j ) = C первых интегралов [23]. При постоянных n x , n _у первые интегралы уравнения (12) равны

c1 = x— nxt, c2 = E/exp[(k /nx)x], c3 = E/exp[(k/ny)уj.    (13)

Значения инвариантов c_j восстанавливаются по начальным и граничным условиям. В частном случае, скорость n x = dx / dt определяет изменение возраста x человека со временем, скорость n y = dy / dt характеризует варьирование серьезности у его заболевания. Обычно считается, что n x = 1 т.е. возраст соответствует течению времени, но полагают также, что существует биологический возраст, когда, например 1 > n x >  0 т.е. процесс старения замедляется, что характерно для стран с высокой продолжительностью жизни. Тогда, как следует из (13), E = c 3 exp l ( k / n y ) x l — опасность инфицирования будет экспоненциально увеличиваться с возрастом x с темпами более высокими в благополучных странах. В случае с COVID-19 данные свидетельствуют [18], что наибольшему риску подвержены пожилые люди с большим различием возрастных тенденций по государствам. При n x <  0 зависимость от возраста будет обратная, как это было во время пандемии 1918 г., когда 99% людей,умерших от гриппа и его осложнений, были моложе 65 лет [1]. Судя по инфографикам, преобладают легкие формы у ® 0 COVID-19, что, как следует из (13) E = c ₃ exp [( k / n x ) у | , соответствует ситуации n _у <  0 . По степени летальности у , где n _у >  0 , новый коронавирус имеет невысокие показатели p = 0,036 в день [24].

Опираясь на перечисленные формулы, появляется возможность количественно оценить национальные показатели управления пандемией по особенностям реакции населения на распространение нового коронавируса. Использовались данные из различных источников по изменению во времени величины установленных случаев заражения населения I ( t ) разных стран вирусом COVID-19. Данные обрабатывались численными методами по указанным уравнениям. Суточная скорость изменения характеристик рассчитывалась по формуле V ( t ) = E ( t ) — E ( t — 1 ) Связи устанавливались методами корреляционного и регрессионного анализа, в ходе которого решалась обратная задача моделирования — определения информативных коэффициентов модели по временным рядам данных [15].

На первом этапе обработки данных по территориям, где население широко охвачено пандемией коронавируса (табл. 1), проверялась гипотеза связи опасности E ( t ) и риска p ( t ) по уравнению (7), что соответствует пропорции p = kE с индивидуальным коэффициентом ПР k ₁ для каждой страны. Он дает первую оценку k для расчета по модели (3). Коэффициенты определялись с корреляцией R >  0,95 зависимости p от E и E от t и в основном подтверждают справедливость экспоненциальной функции опасности (3). Для p ( E ) худшие результаты аппроксимации имеются по материалам Китая, поскольку здесь данные не обладают необходимой гладкостью: есть сильно «выскакивающие» значения.

В эту формулу не укладываются данные по США, где по вычисленному ПР на середину апреля должно быть не более 104 ты- сячи зараженных против 10-кратного превышения этой величины в реальности. Зависимость S0 от упомянутого индекса готовности f положительна (R=0,63), т.е.

считавшиеся по расчетам наиболее подготовленные к пандемии страны, оказались реально более уязвимыми.

Для понимания национальных особен-

Таблица 1

Основные показатели эпидемического процесса коронавируса COVID-19 по разным странам на середину апреля 2020 г. (пояснения в тексте)

Table 1

Key indicators of the epidemic process of COVID-19 coronavirus in different countries by mid-April 2020 (explanations in the text)

Страна	k 1	S 0	t 0	tm	k	k 0	g	f
США	0,159	850	33	99	0,163	0,572	0,00427	83,50
Испания	0,128	190	56	97	0,128	0,641	0,00556	65,90
Италия	0,082	175	50	93	0,094	0,579	0,00552	56,20
Франция	0,113	167	56	95	0,112	0,777	0,00791	68,20
Германия	0,141	141	54	96	0,143	0,642	0,00562	66,00
Великобритания	0,109	120	59	107	0,141	0,527	0,00395	77,90
Китай	0,0164	83	0	38	0,152	0,711	0,01555	48,20
Россия	0,179	95	67	112	0,175	0,439	0,00287	44,30

Источник: Рассчитано автором по данным — Пандемия COVID-19. Материалы Википедии [Электронный ресурс] — Режим доступа: ; Global Health Security Index.— [Электронный ресурс] — Режим доступа: uploads/2019/10/ (дата обращения: 16.03.2020).

ностей управления ситуацией исследуется зависимость ln E ( t ) по разным странам (рис. 1). Теоретически она должна быть линейной от t , что идеально проявляется в России, в других странах в начальных фазах процесса, а в КНР — нелинейна с низким значением ПР k 1 = 0,0164/ день. При таком значении экспонента E ( t ) становится линейной функций времени, что характерно для физико-технических систем [21], когда надежность P * ( t ) падает по экспоненте.

При расчетах по формулам необходимо знать значения t0 , tm и S , которые точно определяются на основе статистических данных по началу, пику и окончанию эпидемического процесса. Время t0 здесь соответствует моменту, когда в стране выявлены первые 10 инфицированные новым коронавирусом больные. Разница At = tm -t0 равна времени развертывания процесса — сумме длительности фазы экспоненциального роста At0 = t -t0 и пред-пикового периода Atm = tm -t (начала вы-полаживания кривой прироста установ- ленных случаев заражения). Этими параметрами определяется линейная зависимость (9) величины ПР k от максимально возможного по текущим оценкам потенциала заражения S0: k = - 0,00052S0 + 0,207, R = -0,80 .

Сравнение k и k1 , найденных разными способами (табл. 1), сопоставимы: k = 0,65k1 + 0,060 (R = 0,76). Получается, что значение k на треть меньше k1 , что обусловлено большей сложностью функций связей, чем предполагалось. Это определено отклонением от линейной тенденции изменения lnE(t) (см. рис. 1) по формуле (10) и детерминируется значением k(t), которое зависит от времени и является управляемой величиной. Такое значение вычисляется по статистическим данным глобального мониторинга пандемии k(t) = p(t) / E(t) (рис. 2). Величина k(t) варьирует во времени t, проявляя общую тенденцию снижения с коэффициентом g (табл. 1): k(t) = k0— gt. Показатель первичной ПР k0 отражает неготовность системы национального здра- воохранения к началу пандемического процесса; он понижается при более позднем начале эпидемии t0 . Соответственно готовность будет противоположной по знаку величиной Aк0 = к0K — к0, вычисляемой, например, относительно китайской ПР k0K . Показатель g характеризует управляемость социально-экономической системой. Самая высокая неготовность к 0 K =0,777/день (готовность A к0 = 0) была в Китае, первым встретившим эпидемию коронавируса, самая низкая k0 = 0,439 (повышенная готовность Ak0 = 0,339) — в России, что последняя вошла в пандемический процесс из перечисленных стран. Напротив, самая высокая управляемость g = 0,0156/день2 характерна для Китая и самая низкая g = 0,00287 — для России, медленно снижающей приемлемый риск с одинаковыми темпами g до конца мая. Если такая закономерность понятна с учетом особенностей государственного устройства Китая, власти которого жестко ограничили передвижение населения и обеспечили его изоляцию, то высокие показатели регулируемости (табл. 1) в «свободных» и «открытых» западных странах, например, g = 0,00791 во Франции, удивляют. Здесь темпы снижения ПР намного больше российского показателя g управления «непослушным» населением. В связи с этим можно также полагать, что население западноевропейских стран более ответственно отнеслось к ситуации, чем российское общество. Вместе с тем, из-за особенностей поведения населения, политики правительств, их специфической оценки опасности эпидемии относительно низкая государственная управляемость пандемией проявилась в Великобритании g = 0,00395 и США g = 0,00427/ день2. По данным табл. 1 прослеживается линейная положительная зависимость к0= 0,793gtm + 0,204 (R = 0,97). Отсюда требуемый уровень постоянной готовности Aк0 снижается при увеличении управляемости g и отдалении момента tm проявления пика эпидемии.

Высокая подготовленность системы здравоохранения России обеспечила сна- чала оптимистичный сценарий управления социально-экономической и эпидемической ситуацией, позволивший пролонгировать момент начала массового инфицирования и пика заболевания. Для этого с 20.02.2020 г. был введён запрет на въезд на территорию России граждан Китая. С 17.03. прекращено железнодорожное и авиасообщение с зарубежными странами. 25.03. для борьбы с распространением эпидемии период с 30 марта по 3 апреля объявлен нерабочим, который продлен до 30 апреля, а затем — до 11 мая с целью максимального сохранения здоровья и жизни населения. Главы администраций регионов России получили дополнительные права и обязанности, позволяющие принимать во внимание местную специфику коронавирусной ситуации. Вместе с тем в начале апреля стало ясно, что население России не в полной мере осознает опасность и необходимость соблюдения мер противодействия эпидемии — режима самоизоляции и социального дистанцирования, в чем выразилась низкая управляемость ситуацией со стороны руководства страны и регионов и появилась необходимость введения более строгих мер в г. Москве и в других субъектах Российской Федерации. Текущие расчеты по модели начала апреля указывали на 112 день пандемии (21 апреля 2020 г.) как момент достижения пика (плато) развития эпидемии в России. Однако в начале мая наблюдался новый всплеск заражения с ежедневным приростом более 10 тыс. человек. С позиции принятой модели популяционная система постоянно меняется с коррелированным смещением параметров списка таблицы 1, что снижает предсказуемость развития процесса. Необходимо в наблюдаемых отклонениях выявить закономерности, связанные с потерей управляемости, чтобы не только поддерживать (g = 0) в стране постоянный уровень ПР 0,08/день, но и не допускать ее перехода в отрицательную область g < 0 неуправляемости.

Разрабатываются модели и методы расчета количественных показателей реакции национального государства и общества на опасность распространения коронавирусной инфекции COVID-19 в начальной фазе эпидемии. Полученные результаты сохраняют свою актуальность в процессе развития пандемии, добавляя новые знания о явлении. Используются понятия, модели и методы теории надежности описания развития эпидемической ситуации функциями (2)-(6) вероятности безотказной работы (выживания, сохранения здоровья), плотности вероятности (распределения) отказов (темпов инфицирования), интегрированной опасности заражения, интенсивности отказов (риска заболеть), приемлемого риска, управляемости эпидемической ситуацией. Управление осуществляется через давление власти на величину приемлемого риска (допустимой заболеваемости). По результатам статистической обработки данных по числу подтвержденных случаев заболевания населения разных стран проведен сравнительный анализ процесса развертывания эпидемии в национальных обстоятельствах борьбы с пандемией.

Функции надежности основаны на двойной интерпретации уравнения (7, 11– 12) изменения меры опасности во времени и по факторам развития эпидемического процесса, в частности, учитывается возрастная структура населения. Базовым для математического и статистического анализа является экспоненциальное уравнение опасности (3), в полулогариф- мической шкале представленное линейной зависимостью от времени, искажения которой за счет варьирования управляемой величины приемлемого риска указывает на национальные особенности регулирования эпидемической нагрузки на население.

В Китае реализован упрощенный вариант регулирования этим процессом с высоким уровнем риска, низкой первичной подготовленностью санитарно-эпидемиологических служб и с жесткой управляемостью изоляцией населения. Западные страны, такие как Италия и Франция, характеризуются средней подготовленностью и управляемостью эпидемиологической обстановкой. Изменчивость ситуации в начальный период эпидемии лучше всего моделируется указанными методами на примере населения России, для которой свойственна высокая подготовленность и низкая управляемость обществом в критической ситуации. Текущие расчеты по данным начала апреля 2020 г. указывают на 21 апреля как момент начала формирования пика развития эпидемии в России, но в начале мая произошло нарушение этой тенденции с потерей управляемости и с отложенным максимумом кривой инфицирования (132 день 11 мая 2020 г.). Полученные результаты подтверждают работоспособность модели в ясных терминах теории надежности и определяют направления ее совершенствования в условиях продолжающейся глобальной пандемии по вновь возникающим данным и обстоятельствам для лучшего понимания особенностей протекающих процессов по странам.