Надкритические конвективные течения талой воды в открытой горизонтальной прямоугольной области с заданным вертикальным тепловым потоком

Возникновение конвекции в подогреваемом снизу горизонтальном слое жидкости с температурной инверсией плотности и свободных недеформируемых границах исследовалось в [1]. Рассмотрен случай изотермических границ, обнаружено жесткое возбуждение конвекции. Нелинейную зависимость плотности воды от температуры автор работы Г. Веронис предложил аппроксимировать простой квадратичной формулой, которая в современных обозначениях имеет вид:

P=P m (1-«2 \T — Ti\2 ) ,

где р_т — плотность при T = T , T

температура инверсии плотности, а₂ = 0,8 -10 5 (°С) ²

эмпирический параметр. Такая зависимость с высокой степенью точности описывает поведение чистой воды при нормальном давлении в интервале температур от 0 до 8 °С, температура инверсии при этом составляет T = 4 °С.

В [2] численно (конечно-разностным методом) исследован случай заданного постоянного теплового потока на нижней границе. Критические числа Релея оказались меньше, чем найденные по линейной теории.

Изучение линейной устойчивости механического равновесия слоя с твердыми границами проводилось в [3–6]. Показано, что задача устойчивости равновесия слоя жидкости с инверсией плотности при условии твердых изотермических границ математически эквивалентна задаче устойчивости течения Куэтта между вращающимися цилиндрами. При этом отношение скоростей вращения внутреннего и внешнего цилиндров играет роль, аналогичную роли отношения глубины устойчиво стратифицированной части слоя к его полной толщине. Получена простая алгебраическая формула, связывающая число Тейлора и число Релея. В [3] рассмотрены случаи фиксированной температуры и фиксированного теплового потока на границах. Теоретическое и экспериментальное исследования влияния инверсии плотности на возникновение конвекции в горизонтальном слое воды с твердыми изотермическими границами осуществлено в [4]. Как аналитические, так и экспериментальные результаты показали, что наличие инверсии плотности приводит к стабилизации равновесия слоя. В [5] численно изучалось влияние положения точки инверсии плотности внутри слоя на критическое значение числа Релея и интенсивность надкритических конвективных течений с прямоугольной (в проекции на горизонтальную плоскость) формой ячеек. Для определения условий возникновения конвекции в горизонтальном слое воды вблизи точки экстремума плотности в работе [6] использовалось уравнение состояния р = р_т ( 1 -а | T - T |^У) , основанное на измерениях изменения плотности как чистой, так и соленой воды. Воде с различной соленостью соответствовали разные значения параметров а и у . Установлено, что эффекты, связанные с наличием инверсии плотности, играют стабилизирующую роль.

Устойчивость слоя воды, образовавшегося в результате плавления льда, нагреваемого сверху постоянным радиационным потоком (на верхней границе задан тепловой поток) исследовалась в [7]. Нижняя граница слоя жидкости имела температуру плавления 0°С. Температурная зависимость плотности полагалась кубической. Теоретически и экспериментально показано, что критическое число Релея зависит от температуры свободной поверхности Т ₂, если Т ₂< 8 °С, и не зависит от Т ₂ при Т ₂ > 8 °С.

Линейный анализ устойчивости равновесия проведен в [8] с учетом термокапиллярного эффекта и тепловых условий третьего рода на верхней свободной границе; нижняя граница считалась твердой и изотермической. Принятая в этой работе аппроксимация температурной зависимости плотности в виде кубического полинома дала возможность рассмотреть задачу в более широком температурном интервале, чем при квадратичной зависимости.

Влияние конечной теплопроводности массивов исследовалось в [3]. Анализ случая двух твердых массивов, показал, что при наличии температурной инверсии плотности конечная теплопроводность массивов, как и в отсутствие инверсии, ведет к дестабилизации. Качественная зависимость критического числа Релея от толщины устойчиво стратифицированного слоя R = 1 - z_t (для учета влияния инверсии плотности использовалась безразмерная координата точки инверсии плотности z ) не зависела от граничных условий. Совместный эффект как от максимума плотности, так и от конечной теплопроводности массивов, при больших отрицательных R ( z >>  1) приводил к дестабилизации величины числа Релея относительно буссинесковского предела Ra_c = 1708, а при увеличении R (уменьшении z ) наблюдалась ее стабилизация.

В [9] путем расчетов спектральным методом на суперкомпьютере МГУ (г. Москва) изучались особенности развитой проникающей конвекции с максимумом плотности в середине горизонтального слоя воды, находящегося между свободными недеформируемыми плоскостями. Надкритическое течение полагалось периодическим, и для выбранной длины ячейки периодичности показано существование двух основных ветвей гистерезиса, на которых решения отличаются характерным масштабом. Через квазипериодические режимы и перемежаемость в течении описан переход к хаосу.

Задача конвекции воды, плотность которой квадратично зависит от температуры и давления, рассмотрена в [10]. Определены пределы применимости для конвекции в озере Байкал формулы Верониса (1). С этой целью методом линеаризации исследовался характер равновесного состояния горизонтального слоя воды толщиной до 1000 м со свободной границей по отношению к малым возмущениям. Обнаружено, что состояние механического равновесия слоя воды является неустойчивым. Построены нейтральные кривые и найдены критические числа Релея. Проведено сравнение с результатами решения аналогичной задачи для предельного случая, когда плотность определяется по формуле (1). Показано, что применимость выражения Верониса ограничена глубиной слоя до 150 м, тогда как средняя глубина Байкала составляет 750 м.

В работе [11], соавторами которой являются и авторы настоящей работы, выявлено, что в единственной известной работе [3], посвященной анализу конвекции в горизонтальном слое жидкости со свободной верхней и твердой нижней границами и заданным тепловым потоком на обеих границах, при выводе линеаризованных уравнений для амплитуд возмущений потеряны два слагаемых. В результате решения далее корректно сформулированной задачи линейной устойчивости показано, что тепловые условия, соответствующие фиксированному тепловому потоку, способствуют существованию длинноволновых возмущений. Длинноволновые возмущения возможны не всегда, а лишь при достаточно толстом неустойчиво стратифицированном слое, а именно при zt > 5/9 (здесь zt — обезразмеренная по высоте всего слоя толщина неустойчиво стратифицированного подслоя). При z > 0,61 длинноволновые возмущения наиболее опасны. В области z < 0,61 наиболее опасными являются ячеистые возмущения. Определены границы устойчивости для обоих типов возмущений.

В [12] найдена форма критических возмущений в постановке работы [11]. Длинноволновые возмущения имеют вид плоскопараллельного течения, состоящего из двух или более встречных потоков. Форма ячеистых возмущений — это бесконечный набор одинаковых ячеек с плоскими вертикальными границами. В нижней части каждой ячейки располагается интенсивный вихрь, охватывающий область неустойчивой стратификации и проникающий в область устойчивой стратификации. При достаточно малых значениях z над этим вихрем может образовываться один или несколько все более слабых вихрей.

Исследования неустойчивости и структуры критических возмущений, проведенные в [11, 12] можно рассматривать как первые шаги в к постижению более глобальной проблемы — установлению структуры и режимов конвекции в вытянутых горизонтальных открытых прямоугольных полостях с различными аспектными отношениями L (отношением горизонтального размера к высоте) при заданном вертикальном потоке тепла на горизонтальных гранях.

Анализ литературы показал, что в полостях, заполненных жидкостью с линейной зависимостью плотности от температуры, характерная длинноволновая природа неустойчивости, выясненная в рамках линейной теории устойчивости для бесконечного слоя [13], то есть для L = ^ , ярко проявляется уже в умеренно вытянутых полостях: с L = 4, L = 3 и даже L = 2 [14, 15]. В таких полостях надкритическое движение в широком интервале надкритичностей имеет вид одного крупномасштабного вытянутого вихря. При увеличении L критическое число Релея стремится к значению, определенному методами линейной теории устойчивости для бесконечного слоя. В значительно вытянутой полости ( L = 5) только первое надкритическое движение является крупномасштабным; далее с увеличением надкритичности оно испытывает ряд гистерезисных переходов к ячеистой форме конвекции.

Таким образом, длинноволновая природа неустойчивости в жидкости без тепловой инверсии плотности имеет место уже в умеренно вытянутой полости (с аспектным отношением L = 2). В более вытянутых полостях она тоже присутствует, но в сильно вытянутой полости (L = 5) быстро становится неустойчивой, и режим конвекции меняется на ячеистый.

Устойчивая

/

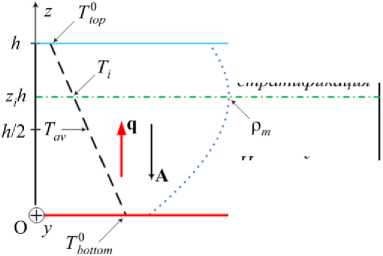
Рис. 1. Геометрия задачи; равновесное распределение

Неустойчивая стратификация температуры  T0 (z)  показано штриховой линией,

g

распределение плотности в состоянии механического равновесия р⁰ ( z ) - пунктиром; штрихпунктирная линия – граница между зонами устойчивой и неустойчивой стратификации; q – вектор теплового

Анализ работ [11, 12, 14, 15] позволяет предположить, что длинноволновая природа неустойчивости в слое талой воды, то есть в жидкости с инверсией плотности, будет обнаруживаться в умеренно вытянутой полости с аспектным отношением L = 2 .

Поэтому целью настоящей работы является исследование конечно-разностным методом устойчивости механического равновесия и надкритических режимов конвекции жидкости с тепловой инверсией плотности в горизонтальной полости с аспектным отношением L = 2 для двух характерных значений положения точки инверсии z = 0,5 и z_i = 0,75 . Выбор значений z связан с тем, что при первом значении в бесконечном слое природа неустойчивости ячеистая, а при втором — длинноволновая.

потока; A – градиент температуры; g – вектор силы тяжести

2. Постановка задачи и метод решения

Рассмотрим горизонтальную прямоугольную полость высотой h и шириной l (Рис. 1), заполненную водой и находящуюся в однородном поле силы тяжести g. На обеих горизонтальных границах z = 0; h задан фиксированный вертикальный тепловой поток q, боковые границы x = 0; l теплоизолированы. Зависимость плотности от температуры принимается квадратичной (1).

Прямоугольная правая декартова система координат ( O xyz ) определена так, что ось O x проходит по более нагретой горизонтальной границе, а ось O z — по левой теплоизолированной вертикальной. Верхняя граница полагается свободной, а все остальные границы твердые.

Для описания движения жидкости применим уравнения свободной тепловой конвекции жидкости с температурной инверсией плотности в приближении Буссинеска [11]:

dv + v-w = -^-Vp + vAv-a2g(T-T)2,(2)

П +v -V T = xA T ,(3)

о t div v = 0 .(4)

Здесь p — добавка к гидростатическому распределению давления в неподвижной жидкости. Коэффициенты кинематической вязкости — v, и температуропроводности — % , считаем постоянными. Термокапиллярным эффектом, эффектами испарения и излучения на верхней свободной границе пренебрегаем. Оценки, полученные в [10], показывают, что в условиях открытых водоемов (прудов, озер) приближение Буссинеска может быть использовано для глубин порядка сотни метров.

Запишем граничные условия:

• - на теплоизолированных вертикальных стенках

x = 0, l :   v = 0,   — = 0;                                   (5)

5 x

- на твердой нижней и свободной верхней горизонтальных гранях

z = 0 :   v = 0,	O T =- A ;                             (6) о z
5 v z = h :    v z = 0,    —x = 0, о z	5v„        ST — = 0,    '  = - A .                     (7) 5 z        5 z

Из содержащихся в (5)-(7) условий для температуры (на горизонтальных границах полости задан постоянный вертикальный градиент температуры, а боковые стенки теплоизолированы) следует, что поступающее в полость через нижнюю границу в единицу времени количество теплоты равно потоку тепла через верхнюю границу. Поэтому средняя температура жидкости в слое T не зависит от интенсивности конвекции и обусловливается только начальным распределением температуры в жидкости.

Задача (2)-(7) имеет решение, соответствующее состоянию механического равновесия:

v0-0,

T* - - Az + Ta, + Ah,(9)

p• = -1 agp.A3h• [T- + Ah2-T -zY + const.(10)

3  2 m     (      Ah        h J

Согласно (9), в состоянии механического равновесия температура на горизонтальных границах постоянна и определяется из выражений:

bottomav

T о - t - Ah .

topav

Введем обозначение

0 bottom

z. = —Ottom-L-----¹

i 00 bottom     top

Подставляя сюда (11), (12) получаем:

T + Ahl 2 - T

Ah

Отсюда видно, что z является безразмерным параметром и в зависимости от соотношения средней температуры жидкости и температуры инверсии может принимать как положительные, так и отрицательные значения.

С учетом (14) выражение (9) для равновесного распределения температуры перепишется в виде:

T ⁰= T + Ah ( z - z[h ) .

После подстановки (15) в (1) имеем распределение плотности в состоянии механического равновесия:

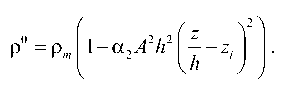
P ⁰

Продифференцировав это соотношение по z , получаем:

^ = 2Pma2 A2h (z/h - zi) .

dz

Как видно из формулы (17), при z <  0 во всем слое d р⁰ / dz < 0, то есть в покоящейся жидкости реализуется устойчивая стратификация. При 0 <  z <  1 устойчиво стратифицирована лишь верхняя часть слоя zh <  z <  h , а прилегающий к дну полости слой 0 <  z <  zh стратифицирован неустойчиво (Рис. 1). В этом случае z имеет ясный физический смысл безразмерной толщины неустойчиво стратифицированного слоя и является безразмерной координатой границы между устойчиво и неустойчиво стратифицированными слоями. Из (17) также следует, что при z >  1 весь слой жидкости стратифицирован неустойчиво.

Для средней температуры T и z выполняется соотношение:

T_av - T = Ah ( z - 12 ) .

Таким образом, z , указывающее на положение точки инверсии в равновесном распределении температуры в жидкости, связано простой формулой с положительно определенной средней температурой жидкости, являющейся параметром задачи. Поэтому z также есть параметр задачи, принимающий как положительные, так и отрицательные значения.

Введем в рассмотрение векторные потенциалы:

ф = rot v ,     v = rot у .

Будем полагать, что надкритическое течение плоское: равна нулю y -компонента скорости и все переменные не зависят от y -координаты. Поэтому у векторных потенциалов φ и ψ отличными от нуля будут только y -компоненты, имеющие в плоском случае смысл завихренности и функции тока:

ф = ( 0, Ф ,0 ) ,      у = ( 0, ф ,0 ) .

Также введем в анализ отклонение температуры от температуры инверсии:

Тогда, после осуществления операции rot по отношению к (2) и использования (19), (20), можно получить систему уравнений тепловой конвекции в переменных ψ , ϕ , T :

∂ϕ + ∂ψ∂ϕ - ∂ψ∂ϕ =Δϕ- Gr T ∂ T ,                        (22) ∂ t   ∂ x ∂ z  ∂ z ∂ x            ∂ x ∂ T   ∂ψ ∂ T   ∂ψ ∂ T   1 +-=Δ T ,             (23) ∂ t   ∂ x ∂ z   ∂ z ∂ x  Pr Δψ + ϕ = 0.                                         (24)

Знак тильда у T далее опускаем.

Уравнения (22)–(24) записаны в безразмерном виде. Для этого введены следующие единицы измерения: времени — h ² /ν , расстояния — h , температуры — Ah , скорости — ν/ h , функции тока — ν , завихренности — ν/ h ² , а также безразмерные комплексы: Pr = ν I χ — число Прандтля; критерий подобия Gr , который является аналогом числа Грасгофа и определяется через физические константы задачи как

2 g α A 2 h 5 Gr =      2      .                                               (25) ν 2

Также введем в рассмотрение аналог числа Релея Ra , связанный с Gr и Pr соотношением:

Ra = Gr ⋅ Pr = 2 g α 2 A 2 h 5.                                     (26) νχ

Компоненты скорости выразим через функцию тока:

∂ψ       ∂ψ v x = -     ,     v z =     .                                         (27) ∂ z ∂ x

Тогда условия на твердой нижней и свободной верхней горизонтальных границах принимают вид:

z=0:   ψ=∂ψ=0,   ∂T=-1, ∂z∂z                                         (28) ∂T z =1:   ψ = ϕ= 0,        = -1, ∂z а граничные условия на твердых боковых границах в новых переменных (в безразмерной форме) будут

следующими:

x = 0:    ψ= ∂ψ = 0,    ∂ T = 0, ∂ x ∂ x                                       (29) x = L :    ψ= ∂ψ = 0,    ∂ T = 0. ∂ x ∂ x

Здесь L = l/h — аспектное отношение.

Состояние механического равновесия, когда жидкость покоится, в новых переменных и безразмерной форме описывается уравнениями:

ψ⁰ =ϕ⁰ =0, T ⁰ = z - z .

Выражение (18), связывающее среднюю температуру жидкости с координатой точки инверсии в покое, в безразмерных переменных перепишется в виде:

Таким образом, решение задачи (22)–(29) определяется числом Прандтля Pr , числом Грасгофа Gr , координатой точки инверсии z (или средней температурой жидкости T в полости) и аспектным отношением L .

Задача (22)–(29) решалась численно, конечно-разностным методом, все пространственные производные аппроксимировались центральными разностями на равномерной сетке. Шаг сетки полагался равным h = 164. Аспектное отношение в представленных ниже расчетах равнялось двум ( L = 2). При аппроксимации по времени применялась явная схема с постоянным шагом по времени h ² 10 .

Уравнение Пуассона (24) для функции тока решалось методом последовательной верхней релаксации. Граничное условие для завихренности на нижней и боковых твердых стенках получалось по формулам Тома [16]. Более подробно использованный метод описан в [17].

3.    Результаты расчетов

До выполнения основных расчетов, в соответствии с приведенной выше методикой, проводилась проверка сформулированной модели и разностного метода. Для этого рассчитывалось критическое число Грасгофа на основе хорошо исследованной задачи плоской конвекции в квадратной полости (то есть при аспектном отношении L = 1) с изотермическими горизонтальными и теплоизолированными вертикальными стенками при отсутствии инверсии плотности. Критическое число Грасгофа находилось путем экстраполяции полученной в расчетах на квадратной сетке с шагом h = 164 линейной зависимости квадрата функции тока от чисел Грасгофа в сторону меньших значений и затем сравнивалось с общепринятым значением, рассчитанным методами линейной теории устойчивости. Так было установлено критическое число Грасгофа Gr = 255.

Известно, что для случая теплоизолированных боковых стенок в квадратной полости округленное до четырех значащих цифр критическое число Релея составляет Ra_c = 2585 [18], а соответствующее ему критическое число Грасгофа при Pr = 10 , равно 258,5. Таким образом, в результате проверочного анализа выяснилось, что вычисленное критическое число Грасгофа отличается от определенного с высокой степенью точности методами линейной теории устойчивости менее чем на 1,5%, что свидетельствует об удовлетворительной точности используемых модели и численного метода решения.

Основные расчеты проведены для полости с аспектным отношением L = 2 при двух значениях положения точки инверсии: z = 0,5 и 0,75. Число Прандтля полагалось равным Pr = 10 . По результатам расчетов для каждого из приведенных значений z в области находилось критическое число Грасгофа и исследовался нелинейный надкритический режим конвекции при надкритичности, достигающей нескольких десятков.

• 3.1.    Равная толщина устойчиво и неустойчиво стратифицированных подслоев

При равной толщине слоев ( z_t = 0,5) в состоянии механического равновесия нижний слой жидкости (0 <  z < 0,5) неустойчиво стратифицирован. Поверх него расположен устойчиво стратифицированный слой жидкости. Для бесконечно протяженной в горизонтальном направлении полости ( L = да ) состояние покоя жидкости (30) становится неустойчивым по отношению к малым нормальным возмущениям при превышении числом Релея критического значения Ra_c ( да; 0,5 ) = 2,32•Ю⁴ [11]. Отсюда следует, что критическое число Грасгофа для бесконечно вытянутой полости и принятого в настоящей работе значения числа Прандтля Pr = 10 равно Gr, ( да; 0,5 ) = Ra_c ( да; 0,5)/Pr = 2,32 • 10³.

Рассмотрим влияние плавного увеличения числа Грасгофа на устойчивость механического равновесия. Конечный горизонтальный размер полости, ввиду наличия твердых вертикальных стенок, тормозящих развитие возмущений, приводит, как правило, к увеличению критических чисел возникновения конвективной неустойчивости [13]. Поэтому первая серия расчетов проведена для числа Грасгофа Gr = 3000 в надежде, что оно превысит критическое, пока неизвестное, число Gr_cr ( 2; 0,5 ) для L = 2 . В качестве начального состояния задавались следующие распределения:

< = 0, т» = 0,5- h • к , ф⁰ = ф c . (32) i , k i , k i , k

Начальное значение завихренности ф c во всех узлах сетки полагалось равным 10. При меньших по модулю значениях ф с , например при ф с = 1, происходит, как показали расчеты, затухание возмущения (32) и установление равновесного состояния покоя (30).

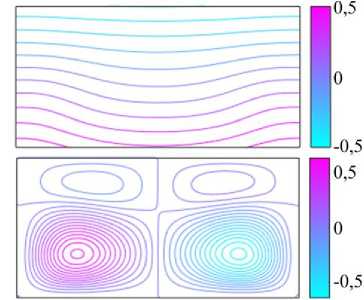
На рисунке 2 а приведено стационарное надкритическое решение, полученное в результате численного расчета эволюции начального состояния (32) c ф c = 10. Вихревая структура надкритического течения соответствует структуре, предсказанной линейной теорией [11, 12] для бесконечного слоя, то есть имеет двухярусный вид по вертикали, с проникновением интенсивных вихрей из нижнего неустойчиво стратифицированного яруса в верхний, устойчиво стратифицированный. Нелинейность приводит к искривлению границы между ярусами, она приобретает волнообразный вид. Похожая структура надкрититических течений наблюдалась для изотермических границ в [2], а также в [19, 20] при исследовании конвекции парогазовой смеси, имеющей, как и талая вода, аномальную зависимость плотности от температуры.

В последующих расчетах, при решении с другими значениями числа Грасгофа, применялся метод продолжения по параметру. За начальное состояние принималось найденное ранее для некоторого числа Грасгофа Gr_t стационарное состояние, затем одномоментно изменялось число Грасгофа на шаг A Gr и путем численного решения задачи с этим состоянием получалось новое стационарное состояние для числа Грасгофа Gr₂ = Gr + AGr. Величина шага по числу Грасгофа A Gr варьировалась от A Gr = 10 до A Gr = 500. Расчеты показали, что такое пошаговое наращивание значения числа Грасгофа от Gr = 3000 до Gr = 14500 приводит к плавному изменению структуры надкритического течения. В каждой из конвективных ячеек центры интенсивных вихрей нижнего (неустойчиво стратифицированного) яруса сдвигаются к твердой стенке, и в каждой из конвективных ячеек происходит отрыв вихрей от нижней твердой стенки, в каждой ячейке формируется слабый, встречный по отношению к основному, вихрь (Рис. 2 б ). Общее число крупных вихрей становится равным шести. Наблюдается строгое разделение течения вертикальной плоской границей на две равные ячейки (режим I).

б

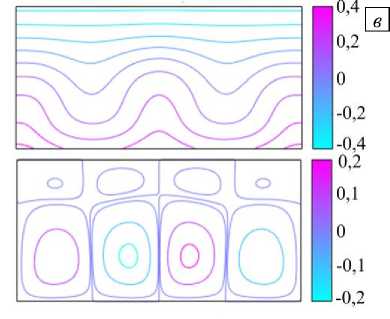
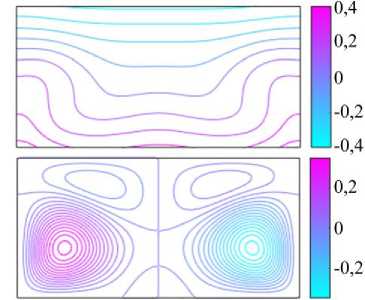
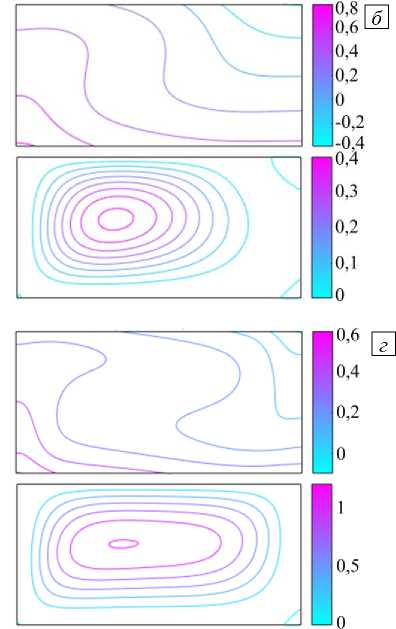
Рис. 2. Изотермы и линии тока режимов I ( а , б ) и II ( в , г ) надкритического конвективного течения при z_t = 0,5

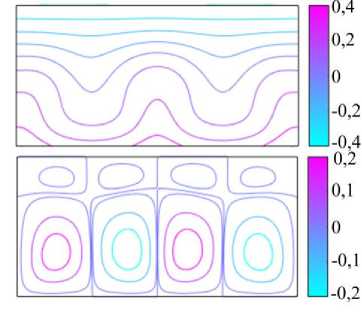
для различных значений числа Грасгофа; режим I: Gr = 3000 ( а ), Gr = 14500 ( б ); режим II: Gr = 14700 ( в ), Gr = 20000 ( г )

Дальнейшее увеличение числа Грасгофа вызывает бифуркацию, заключающуюся в удвоении числа конвективных ячеек по горизонтальной координате (Рис. 2б). Такое стационарое состояние достигается путем увеличения последнего значения числа Грасгофа (Gr = 14500) из режима I на AGr = 200. Наблюдается формирование стационарной вихревой структуры (режим II), представленной на рисунке 2в. Интенсивность конвективного течения в прилегающих к твердым вертикальным стенкам ячейках заметно слабее. Дальнейшее увеличение числа Грасгофа приводит к выравниванию интенсивностей соседних вихрей как в нижнем, так и в верхнем ярусе (Рис. 2г). На рисунке 2г представлено стационарное состояние для Gr = 20000. При уменьшении числа Грасгофа (при Gr = 13000) имеет место переход к предыдущему режиму I c двумя равными ячейками. Переход между режимами — от I к II и обратно — осуществляется гистерезисным образом.

Для количественной характеристики изменения интенсивности надкритических движений с ростом числа Грасгофа воспользуемся зависимостью от Gr максимального по модулю значения функции тока в полости — y_m ( Gr ) , и удельной кинетической энергией конвективного движения — E (Gr), определяемой из выражения:

E ( Gr ) = —JJv² dzdx = —JJ_W dzdx .                        (33)

2 L 00         2 L 00

Рассчитанные зависимости y_m ( Gr ) и E ( Gr ) для диапазона чисел Грасгофа 0 <  Gr <  20000 представлены на рисунке 3. При числах Грасгофа 2600 <  Gr < 10000 кинетическая энергия стационарных решений зависит от числа Грасгофа линейно (зависимость методом наименьших квадратов):

E = 2,66 - 10 ^{- 5} - ( Gr - 2,56 - 10³ ) .

Экстраполируя эту зависимость на нуль, получаем критическое значение  числа Грасгофа

Gr ( 2;0,5 ) = 2,56 - 10³ . Расчеты вблизи этого значения показали, что при Gr=2500 малое начальное возмущение затухает, а при Gr=2600 оно растет вплоть до момента начала установления стационарного режима, похожего на представленный на рисунке 2 а . Учитывая, что в описанных выше тестовых расчетах с известным значением критического числа Грасгофа использованный метод показал точность не менее 1,5%, можно заключить, что экстраполированное значение критического числа Грасгофа будет отличаться от истинного менее чем на 2%. В этом же диапазоне чисел Грасгофа ( 2600 < Gr < 10000 ) выполняется корневой закон для максимального по модулю значения функции тока:

Vm = 3,46-10-3 -4Gr-2,56-103 .

Зависимости (34) и (35) изображены на рисунке 3 штриховыми линиями.

а

Е

0,3

0,2

0,1

°0

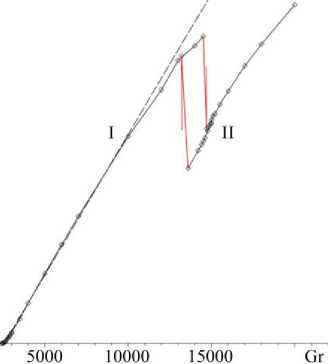
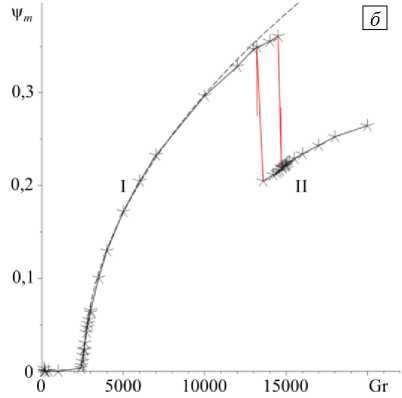
Рис. 3. Зависимости от числа Грасгофа кинетической энергии ( a ) и максимальной функции тока ( б ) в режимах I и II стационарного надкритического конвективного движения в полости для случая z_t = 0,5

Проверочный расчет на конечно-разностной сетке из квадратных ячеек с шагом h = 1/128 для значения числа Грасгофа Gr = 20000 показал, что картина течения до деталей соответствует представленной далее на рисунке 4 г , а значение кинетической энергии отличается от полученного на сетке с шагом h = 164 менее чем на 0,07%.

• 3.2.    Тонкий устойчиво стратифицированный подслой поверх толстого

неустойчиво стратифицированного подслоя

Рассмотрим случай, когда в полости реализуется состояние механического равновесия при нижним слое, состоящем из трех четвертей жидкости в полости (0 <  z < 0,75), неустойчиво стратифицированном, и поверх него расположен слой, втрое тоньше и устойчиво стратифицированный. При бесконечной протяженности полости в горизонтальном направлении ( L = ^ ) состояние покоя жидкости (30) при z >  0,61 становится неустойчивым по отношению к длинноволновым возмущениям при превышении числом Релея своего критического значения, определяемого по формуле[11]:

Ra c ( * ; z ) =

. z- 5/9

Из (36) следует, что критическое число Грасгофа для бесконечно вытянутой полости и принятого в настоящей работе значения числа Прандтля Pr = 10 составляет: Gr ( ^ ;0,75 ) = 165 . Как правило, конечный размер слоя по горизонтали приводит к увеличению критического значения числа Грасгофа. Поэтому первая серия расчетов проведена для числа Грасгофа Gr = 300 в надежде, что оно превысит критическое (пока неизвестное) число Gr ( 2; 0,75 ) . Как и в рассмотренном выше случае z = 0,5, в качестве начального состояния зададим распределения (32) с регулируемым начальным возмущением ф с .

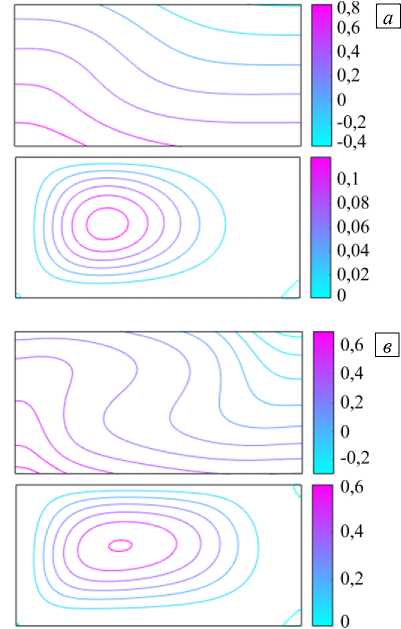
Рис. 4. Изотермы (верхний прямоугольник) и линии тока (нижний прямоугольник) надкритического конвективного течения при z = 0,75 для различных значений числа Грасгофа: 300 (а), 1000 (б), 2000 (в), 20000 (г)

На рисунке 4 а представлено стационарное решение, полученное в результате численного расчета эволюции начального состояния (32) для указанного числа Грасгофа c начальным возмущением ф ^c = 10. Расчеты при существенно меньших по модулю значениях ф с , например при ф ^c = 1, приводили к затуханию возмущенного состояния (32). Как видно из рисунка, надкритическое течение является одновихревым и заполняет всю полость, что говорит о длинноволновой природе неустойчивости.

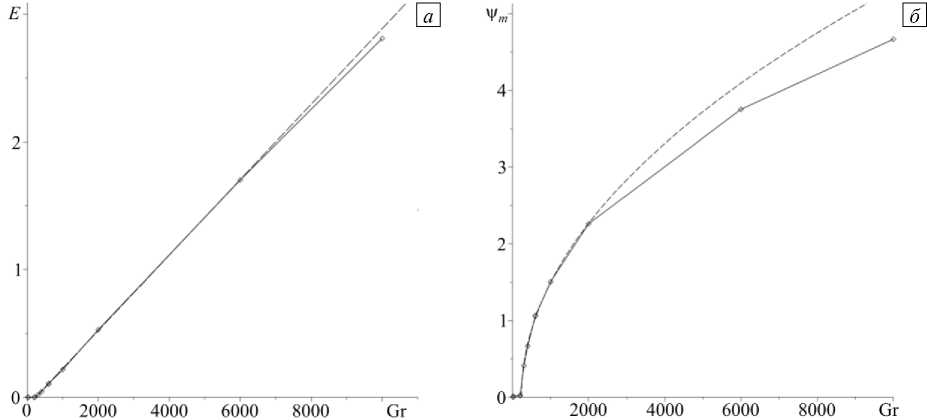
Рис. 5. Зависимости от числа Грасгофа кинетической энергии (a) и максимальной функции тока (б) стационарного надкритического конвективного движения в полости для случая zt = 0,75

Расчеты, показали, что пошаговое увеличение числа Грасгофа от Gr = 300 до Gr = 20000 не приводит к качественному изменению структуры надкритического течения. Оно остается одновихревым, что подтверждает его длинноволновую природу (см. Рис 4 б – г ). Нессиметричность течения обусловлена началом формирования восходящего течения в конвективном пограничном слое около левой вертикальной стенки; в результате центр вихря смещается.. Полученные в расчетах методом наименьших квадратов зависимости y_m ( Gr ) и E ( Gr ) для диапазона чисел Грасгофа 0 <  Gr <  10000 представлены на рисунке 5. В области чисел Грасгофа 250 <  Gr <  2500 кинетическая энергия стационарных решений зависит от числа Грасгофа линейно:

E = 2,96 - 10 - 4 - ( Gr - 2,30 - 10² ) .

Экстраполируя зависимость (37) на нуль, находим критическое значение числа Грасгофа Gr ( 2; 0,75 ) = 2,30 - 10². Расчеты вблизи этого значения показали, что начальное малое возмущение для Gr = 200 затухает, а при Gr = 250 нарастает до установления стационарного режима, показанного на рисунке 4 а для Gr = 300 . Учитывая приведенную выше точность тестовых расчетов задачи для условий с известным значением критического числа Грасгофа, можно полагать, что экстраполированное значение критического числа Грасгофа отличается от истинного менее чем на 2%. В этом же диапазоне чисел Грасгофа выполняется корневой закон для максимальной по модулю функции тока:

_Vm = 1,46 - 10 ^{- 2} - 4 Gr - 2,30 - 10² . (38)

Проверочный расчет на квадратной сетке с шагом h = 1/128 для значения числа Грасгофа Gr = 20000 показал, что картина течения до деталей соответствует представленной на рисунке 4 г , а максимальное значение кинетической энергии отличается от полученного на сетке с шагом h = 1/64 менее чем на 0,04%.

4.    Заключение

Расчеты показали, что в умеренно вытянутой горизонтальной полости с аспектным отношением L = 2 для случая z_t = 0,5, когда толщина неустойчиво стратифицированного слоя 1 - z_s равна толщине устойчиво стратифицированного слоя z , надкритическое течение демонстрирует по горизонтальной координате двухячеистую структуру. Вертикальная структура ячеек имеет сложный двухярусный характер, изменяющийся с увеличением интенсивности подогрева. При z_i = 0,75 структура надкритического течения простая, одновихревая, плавно деформирующаяся с ростом интенсивности подогрева.

При равной толщине устойчиво и неустойчиво стратифицированных слоев (z = 0,5) двухячеистое надкритическое течение в области примерно шестикратной надкритичности гистерезисным образом переходит в четырехячистое течение. Когда же толщина устойчиво стратифицированного слоя 1 - z^ в три раза меньше толщины неустойчиво стратифицированного z = 0,75 , надкритическое конвективное течение в целом приобретает вид вытянутой по горизонтали одновихревой ячейки. С увеличением числа Грасгофа до значения, отвечающего примерно стократной надкритичности, течение остается одновихревым и не испытывает бифуркаций.

Отметим, что с увеличением интенсивности теплопередачи через слой в центральной области полости вблизи поверхности и дна формируется выраженное плоскопараллельное течение (см. Рис. 4 г ). Поэтому в дальнейшем необходимо оценить устойчивость этого плоскопараллельного течения по отношению к плоским ячеистым возмущениям.

Расчеты показали, что при числах Грасгофа, превышающих 20000 на 10÷20%, возникают колебательные режимы конвекции, для рассмотрения и классификации которых планируется проведение дополнительных исследований, в которых предполагается учет термокапиллярного эффекта на свободной границе. Возможно, он может привести к возникновению нового механизма ячеистой неустойчивости.

Исследование выполнено при поддержке РФФИ в рамках совместного российско-германского проекта 20-51-12010 ННИО_а и Министерства науки и высшего образования Российской Федерации (грант № FSNM-2020-0026).