Нахождение импульсных управлений для многозвенных манипуляционных роботов

Рассматривается механическая модель манипуляционного робота, состоящая из конечного набора абсолютно твердых тел, соединения которых описываются идеальными стационарными геометрическими связями. Силовые взаимодействия в системе определяются потенциальными и управляющими силами.

Считаем, что система имеет n степеней свободы и положения манипулятора описываются обобщенными координатами q i ,...,q n . В координатном пространстве R n вектора положений q = (q i ,..., q n )^T принадлежат рабочей зоне D , которая является открытым связанным множеством D ⊆ R ⁿ .

Кинетическая энергия манипулятора определяется формулой:

T = 2 52 a ij (q^q i q j = 2 ^(A(q)^q,^q) , i,j =1

в которой элементы матричной функции A(q) = (aij(q)')'nj=i являются непрерывнымо дифференцируемыми функциями в области D, в каждой точке которой матрица A(q) является симметричной и положи- тельно определенной.

Потенциальное взаимодействие описывается потенциальной энергией П(q) = П(q 1 ,..., q n ), непрерывно дифференцируемой функцией, а управляющие взаимодействия обобщенными силами U i (t), i = 1,n.

Движения манипулятора будем описывать системой канонических дифференциальных уравнений. Обобщенные импульсы определяются формулами:

∂T pi =     , i = 1, n.

^dq i

Вводя вектор обобщенных импульсов p = (pi, ...,pn)T, имеем p = A(q)q,  q = A Hq^.

Функция Лагранжа определяется формулой L(q, q) = T(q, q) — П(q), а функция Гамильтона формулой

H ⁽ q,p) = [^(q,p^{) — L(}q^,q)] q ^ p = 2 ( A -^ qMp ) + ^{П (}q⁾.

Канонические уравнения движения имеют вид [1]:

-    dH (q,p)    .      dH (q,p)            .    --- qi =  5-----, Pi =----+ Ui(t), i = 1,n.          (1)

∂p i                 ∂q i

Требуется найти управления U i (t),i = 1,n, которые позволяют перевести манипулятор из заданного начального положения равновесия q(0) = q ⁰ , p(0) = 0 в заданное конечное положение равновесия q(T k ) = q ^T , P^(T k ) = ^{0 .}

Время перевода T k манипулятора из начального положения в конечное является неизвестным.

При решении задачи будем рассматривать следующее множество импульсных управлений

U i (t) = S 0 5(t)+ S T 5(t — T k ), i = 1n t E [0,T k ],        (2)

где J(-) — функция Дирака.

Импульсные управления генерируемые в начальный момент времени t = 0 служат для перевода манипулятора из начального положения равновесия на специальную траекторию движения в фазовом пространстве R ^{2 n} , проекция которой на координатное пространство R ⁿ соединяет точки q ⁰ и q ^T . При движении по траектории управления выключаются. Импульсные управления генерируемые в конечный момент времени t = T k служат для гашения скорости в конечном положении.

Для решения задачи необходимо определить траекторию движения, соединяющую точки q ⁰ и q ^T в координатном пространстве, время T k движения по траектории из начального положения в конечное положение и силовые импульсы S ⁰ , S T , i = 1,n.

1 Нахождение траектории в координатном пространстве

При движении по траектории управления отсутствуют. При решении задачи используем первые интегралы канонических уравнений

.    dH (q,p)    .      dH (q,p)    .   — qi = —я---, Pi =--^—, i = 1,n, dpi                   d^li которые определяются теоремой Якоби [1]

dW (q,a,h)        . .-----

-----------= b i , i = 1, n — ∂a i

1,    a = (a i ,...,a n- i )^T,

dW (q,a,h)       . -—

-----------= pi, i = l,n, ∂qi dW (q,a,h)

-----.----- = t + t o . ∂h

Здесь a i , b i , i = 1,n — 1, h, to — произвольные вещественные постоянные, W(q, a, h) — полный интеграл уравнения Гамильтона — Якоби для консервативной системы [1]

H

∂W q, , ∂q 1

∂W

= h ∂q _n

Будем полагать, что известен полный интеграл уравнения Гамильтона — Якоби. Например, полный интеграл уравнения Гамильтона — Якоби может быть найден при выполнении условий теоремы Лиувилля [2].

Теорема 1. Пусть векторы начальных положений q ⁰ и конечных положений q ^T (q ⁰ = q ^T ) принадлежат рабочей зоне D, существует единственное решение a i = a i (h),i = 1, n — 1 системы уравнений

∂

da (W(q0,a, h) - W(q ,a, h)) = 0, i = 1,n — 1, и траектория, соединяющая начальное и конечное положения, принадлежит рабочей зоне D , она неявно определяется системой уравнений

∂ da: (W(q,a,h) - W(q ,a,h)a=a(h) = 0, i = 1,n - 1,       (7)

и время движения по траектории из точки q ⁰ в q^T определяется формулой:

T k = T k (h) = dhh ( W (q , a, h) — W(q , a, h)) a = _a(h ) .         (8)

Доказательство. Из (3) следует необходимость выполнения усло- вий

dW (q, a, h) ∂a i

dW (q°,a,h)   ,    . .------T

-------------- = b i , i = 1, n — 1. ∂a i

Тогда из (9) следует необходимость выполнения равенств (6), которые неявно определяют ai = ai(h),i = 1,n — 1. Из равенств (9) с учетом ai = ai(h),i = 1,n — 1 получим уравнения (7) для траектории. Также из равенств (9) находим произвольные постоянные bi и           dW(q°,a(K),K)

i = 1, n — 1.

b i b i ^{( h )}              da i         ,

Из формулы (5) в начальный момент времени t = 0 находим постоянную t 0

,    8W (q°,a(h),h)

^{t 0} =------ dh ------'

и время движения по траектории (7) из начального положения в конечное определяется формулой (8). Теорема доказана.

2 Нахождение силовых импульсов

Для множества допустимых импул ьс ных управлений (2) требуется найти силовые импульсы S 0 , S T , i = 1,n, реализующие перевод манипулятора из начального в конечное положения.

Теорема 2. Пусть выполнены условия теоремы 1. Тогда для перевода манипулятора из начального положения равновесия в конечное положение равновесия используются силовые импульсы, определяемые формулами:

0    ^dW ⁽q ^{0 ,}a⁽h^),h)     ,     ^dW ⁽q ^{T ,a}(h)^,h)       —

S i =----dq----- S i = 8i -----¹ ’ ^n ⁽¹⁰⁾

Доказательство. Интегрируя вторую группу дифференциальных уравнений (1) на отрезках [0, e], [T k — e, T k ], где e >  0, при учете формы управлений (2) и начальных условий, имеем

[^e dH(q(s),p(s)) , Г^e                  я—

P i (e) = —    ------------—ds +     S i 5(s)ds, i = 1,n,

₀         ∂q i              ₀

A        Г^Tk ^{dH (}q^(s),p^(s)) д , Tk сТ;(    т\д • i

^{— p} i ^{( T} k ^{— e)} = ^—             д       ^{ds +} /     S i o ^{( s — T} k ^{) ds}, i = ^{1 ,n}-

T k - ε       ∂q i              T k - ε

При e ^ 0, имеем p,(+0) = S0, i = 1,n,                      (11)

P i (T k — 0) = —S i , i = 1^.                  (12)

Из равенств (4) с учетом равенств (11), (12) находим силовые импульсы (10). Теорема доказана.

3 Нахождение затрат энергии на переход из начального положения в конечное

При движении по траектории управляющие воздействия не действуют и энергия не расходуется. При выходе на траекторию работа импульсных сил определяется формулой [3]

Ao = 2 pT (+0) A-1 (q0 )p(+0), а при сходе с траектории – определяется формулой [3]:

A T = ^— ^p T ^(T k ^{— 0)}A 1 ^{(q T )p(T} k ^{— 0)}.

Используя интеграл энергии

h(q,p) = 2 (A-1(q)p,p) + n(q) = h, находим работу импульсных сил при выходе на траекторию

A 0 = h - ^{П (q 0} )

и работу импульсных сил при сходе с траектории

A t = -h + П(q ^T ).

Тогда энергия, необходимая для перевода манипулятора из начального положения равновесия в конечное, определяется формулой

E = E (h) = A o + |A t | = 2h - П(q ⁰ ) - П(q ^T ).          (13)

Энергия зависит от произвольного параметра h .

Выбор произвольного параметра h определяет траекторию движения, время движения по траектории, силовые импульсы и затраты энергии на движения. Сформулируем три критериальные задачи выбора оптимального значения параметра h .

Задача 1. Заданы вектор начальных положений q ⁰ и вектор конечных положений q ^T (q ⁰ = q ^T ), принадлежащие рабочей зоне D. Найти значение параметра h 1 , которое удовлетворяет заданному условию ограничения затрат энергии E (h) <  E и соответствует минимальному времени движения манипулятора по траектории при условии принадлежности ее рабочей зоне D :

T k = T k (h i ) = min T k (h).

h ∈ R

Задача 2. Заданы вектор начальных положений q ⁰ и вектор конечных положений q ^T (q ⁰ = q ^T ), принадлежащие рабочей зоне D. Найти значение параметра h 2 , которое удовлетворяет заданному условию быстродействия T k (h) < T k и соответствует минимальным энергозатратам для перехода манипулятора по траектории при условии принадлежности ее рабочей зоне D:

E = E (h 2 ) = min E(h).

h ∈ R

Задача 3. Заданы вектор начальных положений q ⁰ и вектор конечных положений q ^T (q ⁰ = q ^T ), принадлежащие рабочей зоне D. Найти значение параметра h 3 , которое минимизирует комбинированный функционал J , учитывающий время движения манипулятора по траектории, принадлежащей рабочей зоне D, и затраты энергии на это движение:

J(h3) = min J(h) = min (k Tk(h) + E(h)) , h∈R        h∈R где k — задаваемый весовой коэффициент.

4 Пример применения методики нахождения импульсных управлений

Рассмотрим метод нахождения импульсных управлений на примере двухзвенного манипулятора, условно изображенного на рис. 1, состоящего из двух абсолютных твердых тел и совершающих плоскопараллельное движение в вертикальной плоскости. Первое тело совершает поступательное движение вдоль горизонтальной прямой, а второе тело вращается в вертикальной плоскости относительно первого тела. Второе тело цилиндрическим шарниром O 1 связано с первым телом. На конце второго тела укреплен схват, в котором находится перемещаемый объект (груз). Будем предполагать, что линейные размеры схвата и груза много меньше длины второго тела манипулятора и при исследовании движения считать схват с грузом материальной точкой.

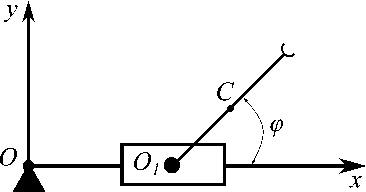
Рис. 1. Двухзвенный манипуляционный робот

Управление плоским движением манипулятора осуществляется при помощи момента M , приложенного ко второму телу, и горизонтальной силы F , приложенной к первому телу. Сила F и момент M создаются двумя независимыми приводами.

Кинетическая энергия определяется формулой:

T = ^( m 1 + m 2 ) x ² — m ₂ lie p sinp + ^ J^d ² .

Потенциальная энергия определяется формулой:

П = — m 2 glsinp.

Здесь x — координата, определяющая поступательное перемещение точки O 1 первого тела; угол ϕ — угол поворота второго тела относительно первого тела; l — расстояние от оси шарнира O 1 до центра масс C второго тела со схватом и грузом; m 1 — масса первого тела; m 2 — масса второго тела со схватом и грузом; J — момент инерции второго тела со схватом и грузом относительно оси цилиндрического шарнира O 1 .

Функция Гамильтона имеет следующий вид:

H = H(x, y,p x ,p ^ ) =

Jp X + 2m 2 lp x p ^ siny + m s p ^ 2(Jm _s — m 2 ^sin ^ y)

+ m ₂ glsiny,

где m s = m i + m2 — масса первого и второго тела со схватом и грузом. Система канонических уравнений Гамильтона имеет вид:

Jpx + m2lsinypv   .   m2lsinypx + mspv px = F (t),

Jm s - m ² ₂ l ² sin ² ϕ ^{, ϕ}    Jm s - m ² ₂ l ² sin ² ϕ ^,

—m ₂ lcosy^m ₂ lsiny(Jp² + m s p ^ ) + p x p ^ Jm s + m 2 l ² sin ² y))

-

P ^                        (Jm s - m 2 l ² sin ² y) ²

— m ₂ glcosy + M (t).

Задача управления состоит в нахождении импульсных законов изменения управляющей силы F (t) и управляющего момента M (t) из множества импульсных управлений (2)

F (t) = S 0 5(t) + S T T — t),

M (t) = S ₂ ⁰ 5(t)+ S ₂ ^T 5(T k — t), обеспечивающих приведение манипулятора из заданного начального положения x(0) = x o , y(0) = y o , rx(0) = 0, yb(0) = 0 в заданное конечное положение x(T k ) = x _T > x o , y(T k ) = y _T > y o , x^ (T k ) = 0, y)(T k ) = 0 за конечное время T k .

При отсутствии управлений каноническая система допускает два независимых первых интеграла. Интеграл энергии

H ^{( x,}y^,P x ^,p _v ) =

Jp X + 2m 2 lp x P _v siny + m s P ^ 2( J m _s — m ² ₂ l ² sin ² y )

+ m ₂ glsiny = h

и циклический интеграл px = ai.

Имеем два первых независимых интеграла: интеграл энергии и циклический интеграл. Эти интегралы находятся в инволюции и согласно теореме Лиувилля система канонических уравнений интегрируема.

Для нахождения полного интеграла уравнения Гамильтона — Якоби используем методику, изложенную в [2]. В результате получим

W (x, y, a 1 ,h) = (x + — cosy)a 1 + m s

+ у Jmnb

— m ² l ² sin ² y )(2 m _s ( h — m 2 glsiny ) — a ² )

2                                      1 dϕ.

m s

Используя теорему Якоби, находим два дополнительных первых интеграла канонической системы уравнений m2l x +--cosy — ms

ar / 7

m s ϕ 0

Jm s - m ² ₂ l ² sin ² ϕ 2m _s (h — m ₂ glsiny) —

a 2 ₁

dy = b i .

11 ϕ 0

Jm s - m ² l ² sin ² ϕ

-—-----——dy = t + to.

2m _s (h — m ₂ glsiny) — a i

Пусть в начальный момент времени t = 0 свободная каноническая система имеет начальные условия x(0) = x o , y(0) = y o , p _x (0) = p X , p ^ = p ⁰ _ϕ . Тогда из начальных условий находим произвольные постоянные a 1 , b 1 , t 0 .

a i = p 0 , b i = x o +-- cosy o , t o = 0.

x             m _s

Из первого дополнительного интеграла находим уравнение траектории

ϕ       Jms - m2l2sin2ϕ ms(xxo) + m2l(c°sy — C°8yo)= px ^ 2m-(h _ m2gUiny) _ (PX)2 dy.

Условие прохождения траектории движения через конечное положение имеет вид:

ϕT       Jms - m2l2sin2ϕ m.txT—Xo)+m2«cosyT—co,yo) = px y^0 у 2ms(h — m2glsin., 2 dy.

Это уравнение неявно определяет p X = p X (h).

Если выполнено условие, то время движения груза до конечной точки определяется формулой:

T k

ϕ T

= Л., V

Jm _s - m ² ₂ l ² sin ² ϕ 2m _s (h — m ₂ glsiny) — (p X ) ²

dϕ.

Используя условие прохождения траектории через конечное положение, преобразуем формулу для нахождения T k . Формулу для закона движения груза по траектории можно преобразовать к виду:

T k = T k (h) =

1 p X ^(h)

m _s (x T — x o ) + m 2 l(cosy T — cosy o ) .

Значения S10 , S1T , S20 , S2T в соответствии с теоремой 2 определяются следующими формулами so = IpXI = —sT , о     (Jms — m2l2sin2^o)(2ms(h — m2glsin^o) — (pX)2) — S°m2lsin^o

S2 =                                                                            , ms

S 2 ^T

^ (Jm s — m^sin^ T )(2m _s (h — m ₂ glsin^ _T ) — (p X ) ² ) — S 0 m ₂ lsin^ _T m s

При нахождении энергии, необходимой для перехода манипулятора из начального положения равновесия в конечное, используется формула (13), в результате получаем следующее значение энергии

E = E(h) = 2h — m ₂ gl(sin^ o + svnp T ).

5 Результаты численного моделирования

В качестве численного примера рассмотрен случай следующих значений параметров системы: m i = 1, m 2 = 3, l = 1, J = 6, g = 9.81.

Перевод схвата необходимо произвести из начального положения xo = 1,  ^0 = n/24, в конечное положение xT = 2,  ^T = n/2.

Рассмотрены три задачи выбора оптимального значения параметра h.

Задача 1. Для заданных начального и конечного положений найти значение параметра h, которое удовлетворяет заданному условию ограничения затрат энергии E (h) < 50 и соответствует минимальному времени движения манипулятора по траектории:

T k = T k (h) = min T k (h).

h ∈ R

Задача 2. Для заданных начального и конечного положений найти значение параметра h, которое удовлетворяет заданному условию быстродействия T (h) < 2 и соответствует минимальным энергозатратам для перехода манипулятора по траектории:

E = E (h) = min E(h).

h ∈ R

Задача 3. Для заданных начального и конечного положений найти значение параметра h, которое минимизирует комбинированный функционал J(h), учитывающий и время движения манипулятора по траектории, и затраты энергии на это движение:

J(h) = min J(h) = min (20 T k (h) + E(h)). h ∈ R        h ∈ R

Таблица 1. Результаты численного моделирования

№	h	p X ( h )	T k ( h )	E ( h )	J ( h )	График
1	41.636	2.034	0.504	50	60.08	Штрих-линия
2	29.465	0.512	2	25.659	65.659	Штрих-пунктирная линия
3	31.3447	1.215	0.8442	29.418	46.3	Сплошная линия

Основные результаты представлены в таблице 1.

На рисунке 2 представлены начальное положение манипулятора (толстой линией) и конечное положения манипулятора (пунктирной линией).

На рисунке 3 представлена трактория движения схвата манипулятора в декартовой системе координат.

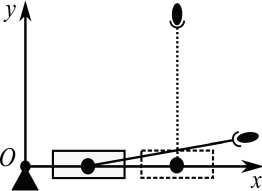
Рис. 2. Начальное и конечное положения манипулятора

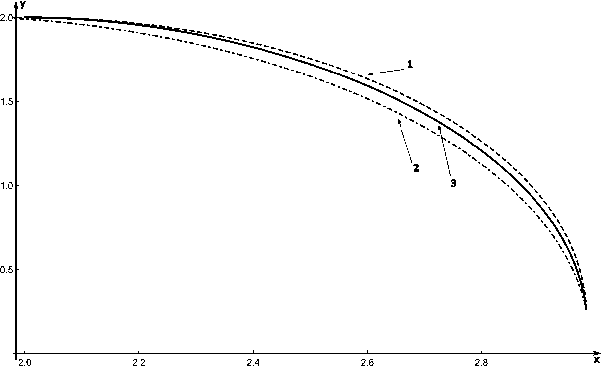
Рис. 3. Траектория движения схвата манипулятора

Заключение

Предложенный метод позволяет построить импульсные управления для многозвенного манипуляционного робота с идеальными стационарными связями. Данная методика была применена при построении импульсных управления для безынерционного [4] и инерционного [5]

двухзвенника, совершающего движение в горизонтальной плоскости. Переход к описанию движения двухзвенника в вертикальной плоскости усложняет задачу.