Нахождение крайних точек суммы двух политопов

DOI:

1.    Вспомогательные сведения

Приведем некоторые базовые понятия и результаты теории выпуклого анализа, которые упростят понимание основных результатов (см.: [1; 5; 6]). Пусть множество Л состоит из точек а ₀ , ..., а _т пространства R ” .

Определение 1. Выпуклой оболочкой conv Л множества Л называется наименьшее выпуклое множество, содержащее Л.

Определение 2. Множество Р = conv { a ₀ ,..., а _т } назовем политопом.

Определение 3. Точка р политопа Р называется крайней, если она не принадлежит выпуклой оболочке никаких двух отличных от нее различных точек политопа Р.

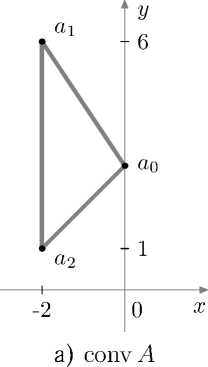
Проиллюстрируем введенные понятия. Рассмотрим множество Л, состоящее из трех точек на плоскости:

Л = _{{а о} ,« 1 ,« 2 _} =   0, -Д^-2).                    (1)

На рисунке 1, а) треугольник со своей внутренностью соответствует множеству conv Л, а вершины являются крайними точками.

Определение 4. Пусть подмножество С является частью пространства R ” . Множество

К (С) = {Лж | Л > 0, ж Е С} называется конусом, порожденным подмножеством С.

Если множество С — выпуклое, то К (С ) также является выпуклым множеством. Заметим, что К (С ) необязательно содержит начало координат.

Определим несколько необходимых нам множеств. Пусть все точки а _г из множества Л отличны друг от друга и являются крайними для политопа conv Л. Зафиксируем индекс i Е 0 : т. Вычтем а _г из остальных точек Л и зададим множество

Л(а ^ ) :— { ао — a ^ ,a i

- а _{ , ... ,а » - 1 — а ₄ ,а г+1

а г ,...,а _т

^{— а} г ^} .

Отметим, что в множестве Л(а _г ) отсутствует нулевой вектор.

Обозначим выпуклый многогранный конус, натянутый на множество { convЛ — а _г }\ \ 0 _п , следующим образом

К(а _г ) :— К (convЛ(a _г )).

Рассмотрим пример. Для множества (1) получим Л(а ₀ ) и К (а ₀ ) (см. рис. 1):

Л'а о ) — {( з^— 2 )} -

Аналогичным образом определим множества В(Ь _г ), К(Ь _г ) для набора точек В = = { Ь 0 ,Ь 1 ,... ,Ь _{т ь} } , где все Ь _г Е R ” отличны друг от друга и являются крайними для политопа conv В.

Под алгебраической суммой политопов conv Л и conv В понимаем conv Л + conv В := {а + Ь | а Е conv Л, Ь Е conv В}.

Заметим, что выражение (2) также называется суммой Минковского.

2.    Крайние точки суммы политопа и отрезка

Приведем рассуждения для нахождения крайних точек сложения политопа с отрезком.

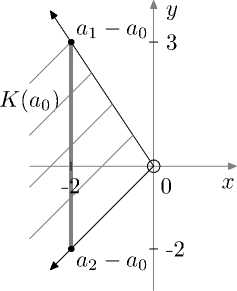
б) К (а о )

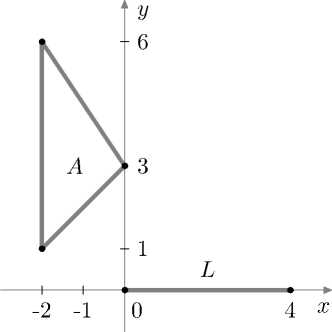
а) Треугольник conv А и отрезок L

Рис. 1. Изображения выпуклой оболочки множества А и конуса К ( а ₀ )

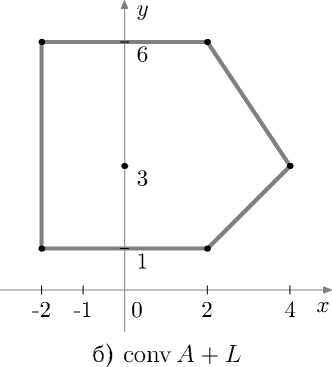
Рис. 2. Сумма политопа и отрезка

Рассмотрим пример. Изобразим сумму S _о треугольника conv А и отрезка L с вершинами в точках (0, 0) ^т и (4, 0) ^т (рис. 2):

• *™ А + L = conv{Q,(-2) , (f) , ■ , Q , Q}.       (3)

На рисунке 2, б) видно, что точка (0,3) ^т не является крайней для нового многоугольника, поэтому она несущественна для задания результата суммы (3). Точку (0, 3)^т следует идентифицировать и удалить из S _о .

Пусть Ь _о ,Ь ₁ Е R ” , Ь _о = b _i . Согласно (2) сложение политопа conv А c отрезком conv { b ₀ ,b ₁ } образует выпуклое множество S 1 :

S 1 := conv А + conv { b ₀ , b _i } =

• = conv { a о + Ь о , a i + Ь о , ..., a _m + Ь о , а о + b i , a i + b i , ..., а _т + b i } .           (4)

Выражение (4) можно переписать, как сумму точки и множества

S 1 = b ₀ + conv А, _и ,                                  (5)

где А _у = { а о , a i ,..., а _т , а о + v, a i + v,..., а _т + у } , у = b i - Ь о .

Свяжем описанные множества с приведенными ранее примерами. Выпуклая оболочка S 1 изображена на рисунке 2 б), где Ь 0 = (0,0) ^т , Ь 1 = (4,0) ^т и множество A задается в (1).

Рассмотрим другое представление суммы (5) (многогранника и отрезка). Множество convA _y можно получить смещая convA на вектор v, при этом «запоминая» весь след смещения (рис. 3).

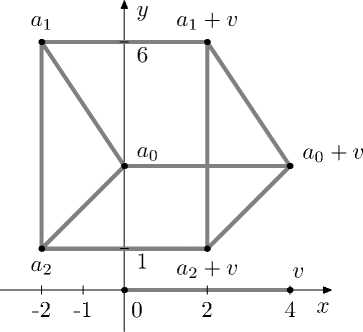
Рис. 3. Множество А ^ и вектор смещения v

В следующей лемме сформулировано правило по выявлению крайних точек множества convA _y .

Лемма 1. Для каждой точки a i из множества А справедливо:

• 1)    Если v ^ К (a _i ) , то a _i + v является крайней для conv A _y .

В противном случае a _i + v не является крайней для conv A _y .

• 2)    Если —v ^ К(a_i), то a_iявляется крайней для convA_y.

3.    Критерий крайности точки в сумме двух политопов

В противном случае a _i не является крайней для convA _y .

Замечание 1. Лемма 1 задает необходимое и достаточное условие крайности точки для суммы политопа и отрезка.

Продемонстрируем графически условия леммы для точек a ₀ и a ₀ + v из рисунка 3. Изобразим конус К (a ₀ ) и векторы v, — v (рис. 4). На рисунке 4 видно, что v ^ К (a ₀ ).

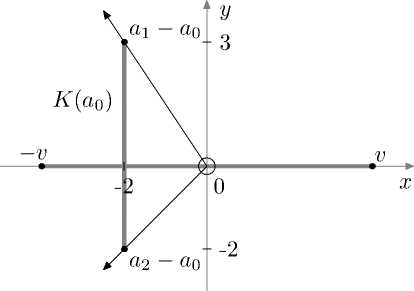
Рис. 4. Проверка условий леммы 1

Получаем, что точка а ₀ + v является крайней. Теперь рассмотрим второй пункт леммы. Вектор — v принадлежит конусу К (а ₀ ). Тогда а ₀ не является крайней.

Перейдем к общему случаю суммы двух политопов (2):

S := conv А + conv В = conv ^J ^J (а _г + b j ).                 (6)

г Е 0:т j E 0 m_b

Сформулируем необходимое и достаточное условие крайности точки для политопа (6). Критерий. Зафиксируем г Е 0 : т и j Е 0 : т _ь . Для того чтобы точка а _г + b j была крайней в политопе S, необходимо и достаточно, чтобы конусы — К(b j ) и К(а _г ) не пересекались.

Проиллюстрируем применение критерия на примере. Зададим множество

В -{©, (—⁶0, ©}-

Рассмотрим сумму (рис. 5)

S -H^W). @. (fX^-GXD-G)}-

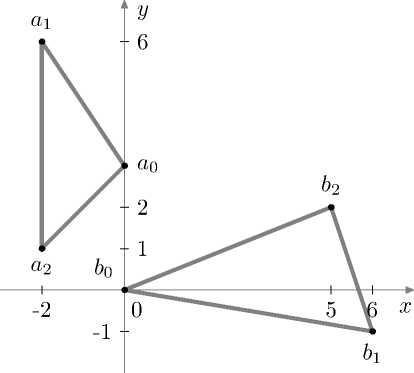
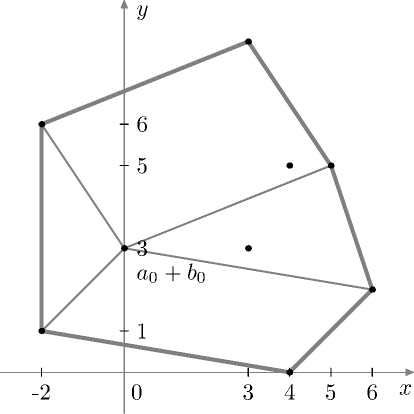
Рис. 5. Сумма двух политопов

Положим г = 0, j = 0 и проверим условия критерия для точки а ₀ + b ₀ , то есть (0, 3) ^Т . На рисунке 6 изображены конусы К (а ₀ ) и К (b ₀ ). Видно, что — К (b ₀ ) пересекает К (а ₀ ). Тогда точка (0, 3) ^Т не является крайней для многоугольника S.

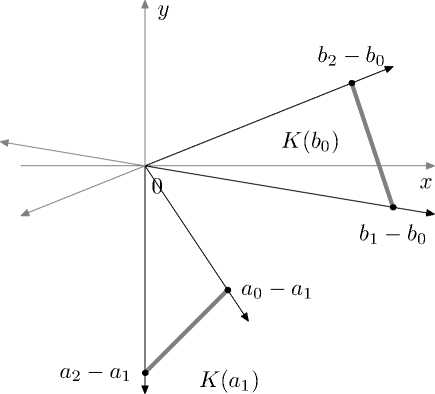
Пусть теперь г = 1, j = 0 и проверим условия критерия для точки а 1 + b ₀ , то есть ( — 2, 6) ^Т . На рисунке 7 изображены конусы К (а 1 ) и К (b ₀ ). Очевидно, что — К (b ₀ ) не пересекает К (а 1 ). Тогда точка ( — 2, 6) ^Т является крайней для многоугольника S .

Более естественно доказывается эквивалентная критерию следующая теорема о некрайности точки в сумме S :

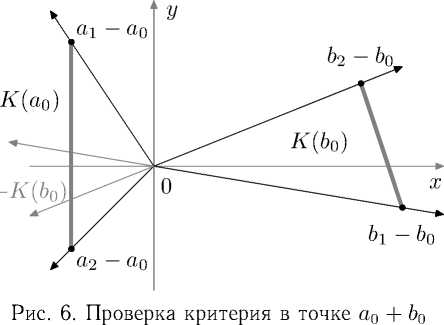
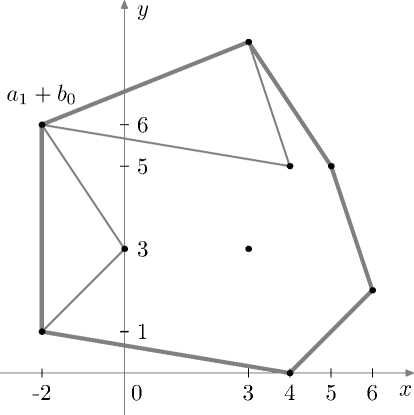
Рис. 7. Проверка критерия в точке а 1 + Ь 0

Теорема. Зафиксируем i Е 0 : т и j Е 0 : т ^ . Для того чтобы точка a _i + b j не была крайней в политопе S, необходимо и достаточно, чтобы конусы — К(b j ) и К(a _i ) пересекались.

Доказательство. Приведем вспомогательные рассуждения.

Пусть точка ж принадлежит политопу convA. Тогда существуют неотрицательные а0, а1,..., От, для которых ж = У^ ак ак,   "^2 ак = 1.

к Е 0:т         к Е 0:т

Если ж = ai, то вектор ж — ai принадлежит конусу К(ai) и представим в виде следующей линейной комбинации ж — ai = «о(ао — ai) + • • • + Oi(at — ai) + • • • + От(ат — ai), где хотя бы один из коэффициентов ак положителен при к Е {0 : т} \ {i}.

Рассмотрим М£ = A(ai)l — вектор с индексом I в множестве A(ai) и аналогично vk = B(bj)к, где I Е 1 : т, h Е 1 : т^. Для ж Е convA справедливо ж — ai = о00п + а1и1 + а2и2 + • • • + атит

52 a i ^ i ,

£С1:т где а = а и а = а^-1 при I Е 1 : г, а = а при I Е г + 1 : т. Следовательно,

У а = 1 — а, то есть 0 6 У «I 6 1.(8)

1 Е 1:т1

Аналогично из у Е conv В следует существование неотрицательных в1, в2, • • •, вть, для которых у - bj = Р1У1 + в2^2 +-----+ втьУть = У вкУк.(9)

к Е 1:т ь

Для любой точки z Е conv А + conv В найдутся, согласно (2), ж Е conv А и у Е Е conv В, для которых z = ж + у. Сложив (7) и (9), получим

Z = (аг + bj)+ У агиг + у вкУк.(10)

1 Е 1:т          К Е 1:т ь

Из определения 3 следует, что для любой не крайней точки с из политопа S найдутся различные точки z, А Е S , для которых векторы z — с и z ' — с противоположны (и потому z + z' = 2с).

Необходимость. Пусть точка аг + bj не является крайней для политопа S. Тогда найдутся различные точки z и z' из S, для которых z + z' = 2(аг + bj).(11)

Представим точки z и z' в виде (10), то есть z = (аг + bj)+ У а£и£ + у вкУк,(12)

1Е1:т          КЕ1:ть z' = (а + bj)+ У а^и^ + У в>к,(13)

1Е1:т          кЕ1:ть где все а^, вк, а'г, вк неотрицательны. Складывая равенства (12) и (13), получим z + z' = 2(аг + bj) — У^ (а1 + а1)и1 + У (вк + вк)ук,

1Е1:т                  кЕ1:ть откуда, учитывая (11), имеем

У (а 1 + а^и е = — У (в к + в' к )У к .                   (14)

1 Е 1:т                       к Е 1:т ь

Вектор в левой части равенства (14) ненулевой (иначе z = z ' = а _г + b j , а это противоречит условию z = z ' ) и принадлежит конусу К(а _г ), а также — К(b j ), то есть справедливо

— К (b j ) Q К (а г ) = 0 .

Достаточность. Пусть конусы —К(bj) и К(аг) пересекаются. Тогда найдутся два ненулевых вектора qa Е К(аг) и q^ Е К(bj), для которых выполняется равенство q« = — qb.                                      (15)

Покажем, что существуют две разные точки z, z' Е S такие, что выполняется z + z' = = 2(a j + b j ).

Согласно определению конусов К (a _t ) и К(b j ) справедливо представление

9а = 52 aiW, 9b = 52 вь^ь, i£1:m                hElvm^

где все коэффициенты al и вн неотрицательны и хотя бы по одному из них положителен. Далее найдем достаточно малое положительное число у, для которого точки z и z' вида z = (а + bj) + у 52 aiW, iG1:m

z' = (а{ + bj)+ у 52 вь^ь кЕ1:ть принадлежат политопу S (см. (10)). Согласно выражениям (7)-(10) коэффициент у должен удовлетворять системе неравенств:

52 ya i 6 1,    52 ув н 6 1.

i E 1:m               h ^ 1:m ^

Выберем любое число γ в пределах

0 < у 6 min *

( E a?)

\i E 1:m   /

- 1

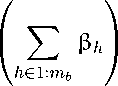
- 1

Складывая равенства (16) и (17), получим z + z' = 2(аг + bj) + у (9a + 9b), откуда согласно (15) справедливо равенство z — (at + bj) — —(z — (at + bj)).

Если z = z' , то в силу (16) и (17) получим, что 9 _а = 9 b . В то же время (см. (15)) 9 _а = — 9 _b . A это возможно, если 9 _а и 9 _b нулевые вектора, что противоречит исходным предположениям.

Получаем, что z = z' и точка a _t + b j принадлежит середине отрезка conv { z,z ' } , то есть a _t + b j не является крайней в политопе S .

Замечание 2. Доказательство леммы 1 проводится аналогично, если вместо конуса К(b j ) использовать вектор v.

4.    Задача линейного программирования

Рассмотрим эффективный способ проверки критерия крайности точки из теоремы.

Вопрос о пересечении конусов К(at) и —К(bj) эквивалентен согласно равенству (14), существованию нетривиального, неотрицательного решения системы линейных однородных уравнений:

£ aiA(a)i + £ вкВ(bj), = 0П.(18)

l E 1:m              h E 1:m b

Чтобы выполнить ограничения, накладываемые на решения системы (18), добавим следующие условия:

Е ai + ^ вк = 1,(19)

l E 1:m      h E 1:m ^

al > 0, I G 1 : m, вк > 0, h G 1 : ть.(20)

Для проверки совместности системы (18)–(20) воспользуемся универсальным приемом [2]. Рассмотрим задачу линейного программирования

Y ^ min,

£ aiA(at)i + £ вкВ(bj)ь = 0», lE1:m               bE1:m^

£ a + £ в ь + Y = 1,                   (21)

l E 1:m      bEhm ^

a _l >  0, I G 1 : m, в ь >  0, h G 1 : т _ь , y >  0.

Заметим, что система ограничений задачи (21) совместна хотя бы для всех a _l , в ь , равных нулю, и γ, равной единице. А также целевая функция ограничена снизу (неотрицательна на допустимом множестве), поэтому задача (21) имеет решение.

Если для найденного решения задачи (21) значение целевой функции γ равняется нулю, то система (18)-(20) совместна, то есть конусы К (a _t ) и — К (b j ) пересекаются.

Предложенный в теореме критерий идентификации крайних точек для суммы политопов использует напрямую конусы, порожденные складываемыми политопами. Известные работы в этой области, например, [3; 4], оперируют нормальными конусами к вышеописанным множествам. Здесь под нормальным конусом, порожденным множеством С , понимается множество

N(С ) = { ж G R ” | ( ж, с ) 6 0,с G С } .

Замечание 3. Критерий крайности точки a _t + b ₃ для множества conv A + conv В может быть сформулирован в виде:

a _t + b j — крайняя О N(К (a _t )) П N(К(b ₃ )) = 0 .             (22)

Обоснование (22) подробно изложено, например, в диссертации [7].

В свою очередь, пересечение нормальных конусов в (22) проверяется решением следующей задачи линейного программирования [3, с. 1270]:

Л о ^ max,

( A(a ^ ) i , Л ) + Л о 6 0, I G 1 : т,

( B(b j ) ь , Л ) + Л о 6 0, h G 1:т ь ,                          (23)

Ло 6 1, где Л G R”, Л0 G R.

Несложно проверить, что задачи (21) и (23) являются двойственными.

Выражаю благодарность неизвестному рецензенту за конструктивную критику, благодаря которой статья приняла свой окончательный вид.

ПРИМЕЧАНИЕ

• ¹    Исследование выполнено при финансовой поддержке гранта СПбГУ № 9.38.205.2014.