Нахождение первых четырех поправок теории возмущений дискретных полуограниченных снизу операторов с произвольной кратностью собственных значений

Рассмотрим дискретный полуограниченный снизу оператор Т и ограниченный оператор Р, заданные в сепарабельном гильбертовом пространстве Н. Пусть {//n}^i - собственные значения оператора Т, занумерованные в порядке возрастания их величин с учетом кратности, а {^n}^Li - его ортонормированные собственные функции, соответствующие этим собственным значениям. Обозначим через ип кратность собственного значения уп операто ра Т, а количество всех неравных друг другу собственных значений уп оператора Т, которые

I P-np + l + M-TLQ |

лежат внутри окружности Тпр радиуса рпо = с центром в начале координат

комплексной плоскости, через по. Пусть {[3n}nV - собственные значения оператора Т + Р, занумерованные в порядке возр астания их действительных частей с учетом алгебраической

кратности. Если для всех п > п о выполняются неравенства q _n =

2 ^ Р II

¹ Pn+v-n.    Pll\

< 1, тогда

no первые то = У Vn собственные значения {Зп }((=1 оператора Т + Р являются решениями n=1

системы т о нелинейных уравнений вида

т р       т ₀      гс

220к = 22 ^к⁺22 ^а !^{р )} ( ^т о ), р = ^о -                    (¹)

к=1      к=1      к=1

(_р)              ( 1) ^к p                            _х1^к,

Здесь ау (то) = Р Sp J у,1 1 Р^ (Т) dу - к-е поправки теории возмущений one-1 по ратора Т + Р целого порядка p, R^ (Т) - резольвент а оператора Т. Известно, что в этом случае в контуре Тпо количество собственных значений оператора Т при возмущении Р не изменяется [1].

Основываясь на системе нелинейных уравнений (1), в работах [2 — 6] был разработан метод нахождения первых собственных значений дискретных операторов, который авторами был назван методом регуляризованных следов (РС).

“    (р)

Если известны значения числовых рядов У^ оу '(т) поправок теории возмущений це- к =1

лого порядка p = 1,то дискретного оператора Т + Р, тогда система нелинейных алгебраических уравнений (1) позволяет находить его первые то собственные значения {/Зп }™=г Предельные абсолютные погрешности найденных собственных значений /Зп оператора Т + Р ~ (рД _ зависят от того, с какой точностью вычислены суммы числовых рядов У^ оу дто).

к=1

В статье [4] разработан численный метод, позволяющий с необходимой точностью вы- числять суммы числовых рядов поправок теории возмущения для возмущенных самосопряженных операторов необходимого порядка. В некоторых случаях суммы числовых рядов “ (рД х

У^ а у ( то ) можно приближенно найти, зная их первые члены, т. к. известно, что ряды к=1

сходятся как геометрический ряд со знаменателем q = max qп [4]. Поэтому важно полу-п чить аналитические формулы вычисления первых поправок акр) (то). В работе [3] найдены аналитические формулы вычисления первых четырех поправок акр)(то) для случая, когда собственные значения оператора Т однократные. В данной работе получены в явном виде формулы вычисления первых четырех поправок в случае произвольной кратности собственных значений оператор а Т.

1.    Вычисление первых четырех поправок теории возмущений дискретных операторов

Пусть все предположения, которые сделаны во введении относительно обственных значений оператора Т выполнены, тогда справедлива следующая теорема.

Теорема 1. Если Т - дискретный полу ограниченный снизу оператор, а Р - ограниченный оператор, действующие в сепарабельном гильбертовом пространстве Н. При этом для всех п>по выполняются неравенства qn < 1. Тогда поправки теории возмущений сккр)(то) для к = 1, 4 и любых натуральных p и по оператора Т + Р вычисляются по формулам по а 1р)(то) = р^

п=1

V      d^A П^{Х) -1}

V пп     u

(А -1)!dр^- ¹

ир~1

Р п

« 2^{Р )} (т о ) =

По          _{Т Т} Г)          т\^ "I

^Р Г    VL    d, ^{п 1}

2 Ч \⁽²⁾ i\ | , А,⁽ У-1 п=1 ⁽ Ап — ¹⁾!Ц у_п

р~1

IP п

+

⁺ ( А⁽¹⁾ -1)!

52 Ут У гп г=п

,\(1)   1

d^{A п 1}

А (!) 1

^{п 1}

Ир п

р— 1 п рп  Рг

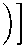
по         Т 7-Т          7\(^) — 1

а з^{Р )} (т о ) =

^Р Г    ^Уг ? п     d^{x п 1} / ч

32^ 1м(з)              ^п п=1 (Ап — 1)!ауп"

С.И. Кадченко, С.Н. Какушкин

3                        д^х-?’- 1 / Д’^{- 1}

j V v и v ■______ ( ^п __

⁺                  /    ^упт1^угт1^упг             I

(²⁾ _ 1)1                р.ДД -1 V Рп - Рг

^{( Ап}      а⁾. i = п             ар_п

+  (1)_1М

⁽ Лп — ^1)! i_Jj=п

Vm Vtj Vjn

(1)   1

d ^{Лп   1}

р— 1 Рп

А " ^{_1 (}Рп Pi^Pп ар п

’

о !^{р )} (т ₀ ) =

п о

V ⁴      d⁾⁾"^{)_ 1}

пп

п=1

( лп⁴⁾ -1)'д р^?- ¹

⁺ (Ап ³⁾ -1)!

V v ² к- v • / J ^V пп ^V гп ^V пi i=п

⁽³⁾ I р— 1

/ДА п ¹ / I I^{р d}       / рп

X(3)  1 V II _

■ЬЛп _ 1 Рп  рг арп

2                                                             .

'    ,----- >  VпiVjп (2V пп Vij + V_mVпj )

⁽ Лп — ^1)! i_Jj=п

(^’ dx" -1

р— 1 Рп

Ац^Х п’- ¹ ЧР п - №⁾⁽^ п - Р-^{) )} Стр п

4      \ -

'     ----- )   Vij VjmVmrnVm

⁽ Ап     ^1)! i_JJ_Jm=п

i\ ⁽¹⁾ 1

d ^{Лп   1}

р— 1 Рп

Др п⁽¹⁾ 1 (^ п - ^i) (^ п - М- j ) (^ п -РтД ’

где Vij = (PwyWj ) - скалярное произведение, { р_п } п=₁ - собственные значения тора Т, {ш _п } п=₁ - ортонорм,ированные собственные функрии, еоответствующие

опера-этим

собственным значениям, v_n - кратность соответственного собственного значения р_п, х (fc) _ Г ^п, ^п > ¹, п =

( k, vп = 1.

Доказательство. Согласно определению первой поправки теории возмущения и теореме о вычетах, имеем

а 1 ^р)Ы = -^^Sp / Д- ¹ [Р^ ( Тфд = 2TU J L _1

Т. о

^Т ” о

^Т ” о

Pшi л

> -------др, wi tP-Рг

,р- ¹

то

Гр       i

^{1 п} о

/1    р г

г р- ¹

•

У У (Pw i ’W i )res------

Р" Р - Р i п=1 i

Обозначим через Vij скалярное произведение (PupUj). Собственные значения рп оператора Т кратности vn- Если г = п, тогда то

, Р- 1

п о

’р- ¹

Рп (р - Pi ) = "  п=1           ¹

п о

> —7-7----- lim

—'  ⁽¹⁾   1 М ^Р"

,=1 ⁽Ап — ¹⁾!

7\(1)   1

d^{x п   1}

А (1) 1

dii ^{п 1}

1Ьр п

п о

1        d^x" ’ ¹

=1 (A? -1)!d Д’" ¹

^р р^{- 1}1

Р п I .

^pР~ ¹

Если г = п res ------ г = 0 . Окончательно получим Р^{п (}Р Рг)

п о

: '/'Пшо' = р^2

п=1

V      d^x'*^{) -1}

пп

(А — 1)! dр^?- ¹

и р- ¹ ) Р п I •

Рассмотрим вторую поправку:

4кг т„о

2                      ■

Шпф, Шп

Т"о ршг

Т"о т0

, Р-1

п=1 ij

^" (р- jUi)(jU- Pj ) '

Возможны следующие варианты вычисления вычета:

1) /П = Pm Pj = Рп то

, Р- ¹

п о

1        d^x" ^{) 1}

п^1    (р- р-⁽(р -Pj )

' р- ¹ \

;

(1)           А^’

,=i (Ап — 1)! dр^{Хп -1} / Рз

т о

г Р- ¹

п о

, Р- ¹

Таким образом,

п^1 Рп ⁽р- р.⁽(р- Pj )

(                (2)

⁽^   Р^ ^л"

п о

,Х 'Л 1

dA п 1

п=1

(2) m,      \(2) 1

⁽Ап -^d Рп"  ¹

и р~ ¹ 1

Р п ) •

(р) а 2

Р

^(т 0 ⁾    ₂

п о

п=1

A^rm      d^X ^^ ^-1

( а!.²⁾ -1)! dp. п-’-¹

⁺ (А ⁽¹⁾ -1)!

□

С.И. Кадченко, С.Н. Какушкин

2.    Численный эксперимент

Для проверки полученных формул (2) в случае кратных собственных значений невозмущенного оператора Т рассмотрим спектральную задачу для оператора Лапласа. Пусть опе- У ²     У ²

ратор Т = — Д задан на прямоугольнике П = 0, al X [0, bl с границей Г. Здесь Д =    +

Ух ² оу² - оператор Лапласа. В качестве возмущения Р возьмем оператор умножения на дважды непрерывно дифференцируемую функцию р ( х,у ), определенную на прямоугольнике П.

Рассмотрим спектральную задачу

(Т + Р )р = p_v, ее D_T .

Dt = {у | р е С ²(П) р|С[П], Др е Ь₂[П] : р| = о}.

Известно, что собственные значения ц_п к и собственные функции ш_п к оператора Т имеют вид:

^И , к²\      , _х 2 . пта .                .----

^к = и + Ь 2) , к ( х,у ) = ^^   -а^-   ”, ^п,к = 1,”.

Система собственных функций {ш_п к } °°к =1 является базисом пространства Т ₂[ П]. В слу- ^{д 2}

чае, когда — рациональное число оператор Т имеет кратные собственные значения. b²

Пронумеруем собственные значения { ц,_п к } °°к=1 и собственные функции {ш_п к } ^ к=1 оператора Т одним индексом в порядке возрастания величин ц_п к с учетом кратности.

В таблицах 1 и 2 приведены результаты вычислений первых собственных значений спектральной задачи (3), найденных методом РС и методом Бубнова — Галеркина. В первом случае собственные значения обозначены /З_п, во втором — 0_п. Причем суммы числовых рядов ° г»ъ

У а к дтц ) в методе РС приближались их четвертыми частичными суммами, используя к=1

формулы (2).

Проведенные расчеты показывают, что результаты вычислений первых собственных значений возмущенного оператора Лапласа методом РС, используя формулы (2) и методом Бубнова - Галеркина хорошо согласуются.

Таблица 1

Собственные значения /З_п и /З_п для возмущенного оператора Лапласа, вычисленных при а =1 , b =1 и р ( х, у ) = х + у

и	/^ п	п	Рп	1 Рп — рп 1
1	19 , 739	20 , 748	20 , 737	0 , 011
2	49 , 348	50 , 356	50 , 347	0 , 009
3	49 , 348	50 , 356	50 , 347	0 , 009
4	78 , 957	79 , 969	79 , 958	0 , 011
5	98 , 696	99 , 708	99 , 695	0 , 013
6	98 , 696	99 , 708	99 , 695	0 , 013
7	128 , 305	129 , 319	129 , 305	0 , 014
8	128 , 305	129 , 319	129 , 305	0 , 014
9	167 , 783	168 , 799	168 , 782	0 , 017
10	167 , 784	168 , 799	168 , 782	0 , 017
11	177 , 654	178 , 672	178 , 653	0 , 019

Таблица 2

Собственные значения /З_п и /З_п для возмущенного оператора Лапласа, вычисленных при а = 2 , b =1 и р(т, у) = (1 + г)ж ⁴ у ²

п	/^ п	Рп	Рп	1 рп	— Рп I
1	12 , 3370	12 , 8462 + 0 , 4278 г	12 , 8443 + 0 , 4266 г	0	002
2	19 , 7392	20 , 5362 + 0 , 7586 г	20 , 5352 + 0 , 7526 г	0	006
3	32 , 0762	32 , 9342 + 0 , 8121 г	32 , 9303 + 0 , 8135 г	0	004
4	41 , 9458	42 , 5287 + 0 , 4998 г	42 , 5247 + 0 , 4945 г	0	007
5	49 , 3480	50 , 0276 + 0 , 6821 г	50 , 0228 + 0 , 6758 г	0	008
6	49 , 3480	50 , 0276 + 0 , 7821 г	50 , 0597 + 0 , 8646 г	0	089