Накопление температурных напряжений в оболочках из полимерных композиционных материалов при циклическом температурном воздействии

Полимерные композиты эффективны при использовании в качестве строительного материала для изготовления газоходов и дымовых труб. Этому способствует выгодное соотношение прочности и собственного веса, стойкость к воздействию агрессивных сред [1], [2], а также возможность управлять свойствами путем изменения структуры [3]. Коррозионная стойкость – главное преимущество перед другими традиционными материалами (например, сталью или железобетоном, сильно подверженным коррозии [4]).

Такого рода конструкции в настоящее время не используют несущую способность материала в полной мере в силу недостаточной изученности его работы в условиях длительной эксплуатации при воздействии температуры, а также малой проработки в нормативной документации (по сравнению с традиционными материалами). Как правило, внешние механические нагрузки воспринимаются поддерживающими конструкциями (решетчатые башни, Zadorin, A.; Mishnev, M.; Korolev, A.

Temperature stress accumulation in polymer composite shells under cyclic temperature impact;

оттяжки, другие трубы при их реконструкции и установке газоотводящего ствола внутрь). При этом имеется успешный опыт возведения несущих стеклопластиковых труб за рубежом. Например, 52метровая труба фабрики по переработке сахара в США (1984) [5]. Это означает, что есть перспективы для повышения эффективности использования композитов в строительстве при заполнении информационных пробелов и внесении необходимых данных в нормативную документацию. Развитие несущих композитных труб и газоходов позволит, во-первых, снизить расходы на строительство за счет облегчения или полного отказа от поддерживающих конструкций, а во-вторых, снизить расходы на эксплуатацию, т.к. металлоконструкции башен подвержены коррозии.

Работа материала применительно к условиям эксплуатации в дымовых трубах и газоотводящих трактах включает в себя ряд, требующих проработки вопросов: влияние температуры на физико-механические характеристики, температурное старение, вязкоупругая работа материала (реология) и т.д.

Вопросы жесткости и прочности при нормальных и повышенных температурах в силу того, что эта тема является актуальной для многих областей применения, достаточно хорошо исследованы. В [6] приводятся кривые напряжений-деформаций для ряда композитов с разной гибридизацией при температурах 25-100°C, а также кривые падения модуля упругости при действии температуры. В [7] проведены испытания трехслойных сэндвичевых систем, состоящих из двух стеклопластиковых обшивок и изолирующего ядра из фенольной пены. Это исследование ценно для нашей области, т.к. стеклопластиковые трубы изготавливаются в том числе трех- или пятислойными. Однако в [7] нагрев производился равномерно с обеих сторон, а в дымовых трубах происходит неравномерное воздействие горячих отводимых газов и холодного наружного воздуха. С одной стороны, это приводит к дополнительным напряжениям от изгиба, а с другой, наружная обшивка остается холодной и дольше не теряет жесткость. В любом случае, анализ воздействия температур на НДС конструкций необходим.

В наших предыдущих работах проводилось как изучение свойств полимеров и композитов при нормальных и повышенных температурах, так и определение их коэффициента линейного температурного расширения (в дальнейшем КЛТР), его нелинейности и взаимосвязи с другими параметрами. Имеются данные о зависимости модуля упругости от температуры и наличия дисперсного наполнителя, а также проведена оценка эффективности применения наполнителей [8]. В [9] приводятся экспериментальные данные о модуле упругости и КЛТР при нормальной и повышенных температурах, подтверждена взаимосвязь этих параметров, а также предложена математическая модель, описывающая ее. Испытания на абразивный износ также показали влияние температуры на работу материала [10]. Значительная часть исследований направлена на прогнозирование и управление свойствами связующего и композита. Имеются данные о конечноэлементном моделировании и вычислении деформационных характеристик стеклопластиков с применением ANSYS Material Designer [11]. Используя совместно с этим имеющуюся математическую модель для связующего, учитывающую температуру [12], можно достаточно точно предсказывать свойства композита.

Температурное старение материала также изучалось нами и другими исследователями. В [13] было установлено, что влияние зависит от значения температуры и может быть как положительным (вызывая эффект доотверждения), так и отрицательным (приводя к деградации материала). То есть, температурный режим конструкции оказывает прямое влияние на ее долговременные свойства. Также изучалось влияние старения на работу в разных условиях [14– 16]. Нами была проведена оценка влияния температурного выдерживания на жесткость и КЛТР материала и сделаны предположения о влиянии старения на внутреннюю макромолекулярную структуру [9], [17], [18].

Вязкоупругая работа полимеров изучалась рядом ученых, и разработаны методы ее описания и предсказания. В статье, посвященной полиэтилену высокой плотности [19] предложена математическая модель, описывающая вязкоупругую работу материала с помощью 7 параметров, определяемых по кривым ползучести и релаксации. Для аналогичного материала был успешно применен [20] метод температурно-временной аналогии [21], позволяющий проводить ускоренные испытания на ползучесть при повышенной температуре. Различные способы моделирования вязкоупругой работы полимеров изучались и сравнивались учеными ранее и позволяют выбрать наиболее перспективные для нашей работы методы. Проведен подробный анализ классических моделей вязкоупругого тела, основанных на комбинациях упругих и вязких элементов [22]. Проведено сравнение теоретических кривых с Zadorin, A.; Mishnev, M.; Korolev, A.

Temperature stress accumulation in polymer composite shells under cyclic temperature impact;

экспериментальными для полимеров, а также анализ применимости классических и усовершенствованных методов моделирования. Сделан вывод, что классические модели, основанные на экспоненциальных зависимостях, не всегда оказываются применимы для реальных материалов.

За счет вязкоупругой работы полимерной матрицы, композиты также оказываются подвержены явлениям ползучести и релаксации [23]. Реологические модели применимы и для них. Имеются данные о сравнении экспериментальных и теоретических кривых ползучести, полученных на основе классической реологической модели [24] и других, например, моделирования молекулярной динамики [25].

Имеются данные о влиянии вязкоупругой природы материала на работу при динамических и циклических воздействиях [26], [27], а также влияние внутренней структуры и расположения армирования [28], [29]. В [26] делается вывод о необходимости учета вязкоупругих свойств. В каждом случае вопросом остается подбор подходящей модели вязкоупругого материала и определение ее параметров под конкретный материал. В целом, методики испытаний на ползучесть проработаны, в том числе в нормативной документации. Однако, т.к. дымовые трубы и газоходы работают в специфических условиях, сочетающих длительное нагружение, длительное температурное воздействие, а также возможны циклические температурные и механические воздействия, требуется разработка и применение модели вязкоупругого материала, учитывающей одновременное нелинейное изменение жесткости, КЛТР и реологических параметров при нагреве.

Одно из следствий вязкоупругой природы полимеров – возможность накопления деформаций и напряжений при циклических воздействиях. Их влияние может быть непредсказуемым, т.к. оно зависит одновременно от вязкоупругих свойств, температурных свойств и условий работы сооружения. Эти вопросы поднимались учеными ранее. Установлено [30], что циклические температурные воздействия приводят к снижению прочности и жесткости материала.

Целью данного исследования в рамках гранта РНФ №23–29–00425 была оценка возможности накопления температурных напряжений в полимерном композите при циклическом нагреве-остужении в стесненных условиях, а также анализ их влияния на напряженно-деформированное состояние конструкции из подобного композита (стеклопластика).

Для этого были поставлены следующие задачи:

• -    Испытать стеклопластиковые образцы на циклическое температурное воздействие с регулярными замерами времени, температуры и действующих напряжений;

• -    Сделать выводы о работе изучаемого материала при циклическом действии температур и оценить влияние остаточных напряжений на напряженно-деформированное состояние конструкции из подобного материала.

• 2    Materials and Methods

Состав полимерного композита, следующий:

• -    Эпоксидная смола KER 828 (аналог ЭД20), Производитель: KUMHO P&B Chemicals;

• -    Изометилтетрагидрофталевый ангидрид (ИЗОМТГФА) (отвердитель для эпоксидной смолы). Производитель: ASAMBLY Chemicals company Ltd., Nanjing, China;

• -    Алкофен (ускоритель отверждения эпоксидных смол). Производитель: АО "Эпитал", Москва, Российская Федерация;

• -    Стеклоткань ЭЗ-200 [31].

Испытания проводились на испытательной машине Tinius Olsen H100KU (Tinius Olsen Ltd., Суррей, Англия) в специально изготовленной камере, оснащенной нагревательными элементами и термостатом (рис. 1).

Рис. 1 – Испытательная камера

Fig. 1 – Testing chamber

Образцы предварительно растягивались до напряжений около 30 МПа для устранения возможных податливостей системы. После этого, около 5 минут ему давалось отдохнуть, чтобы пропустить этап изначальной наиболее активной релаксации, и уменьшить ее влияние на результаты. Температура контролировалась автоматически термостатом, а также проверялась по образцу-эталону с вклеенной внутри термопарой. Различия в температурах в течение испытаний составляли не более 2°C. Минимальная и максимальная температуры циклов составляли 30°C и 100°C соответственно, замеры усилия производились при этих значениях температур. Усилия затем переводились в напряжения путем деления на площадь сечения образца.

Также, для дальнейших расчетов и моделирования работы материала в ANSYS , был определен модуль упругости композита при нормальной температуре.

Для исключения влияния проскальзывания в зажимах удлинение образца измерялось по фиксированной базе с помощью датчиков часового типа с точностью 0.01мм (принципиальная схема см. рис. 2). Датчики устанавливались крест-накрест для исключения влияния перекосов по обеим осям симметрии. Модуль упругости определялся по закону Гука путем деления приращения напряжений о на относительную деформацию £ :

E =

σσ

=⋅ ε ∆ L

Всего было проведено 7 замеров. Среднее значение модуля упругости составило 10006 МПа с коэффициентом вариации 8.8% (таблица 1). В целом, значения модуля для данного связующего и стеклоткани соответствуют результатам предыдущих исследований [11], поэтому работу изготовленной испытательной камеры было решено считать корректной.

Таблица 1. Модуль упругости композита

Table 1. Elastic modulus of the composite

№	∆ σ , МПа	ε , м/м	E, МПа
1	12.315	0.001291667	9534
2	12.315	0.001041667	11823
3	12.315	0.001208333	10192
4	12.315	0.001208333	10192
5	12.315	0.001333333	9236
6	12.315	0.001291667	9534
7	12.315	0.001291667	9534

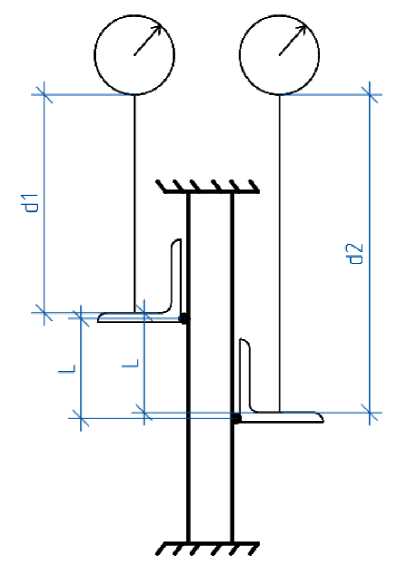
Рис. 2 – Схема к определению модуля упругости

Fig. 2 – The scheme for determining the modulus of elasticity

3 Results and Discussion

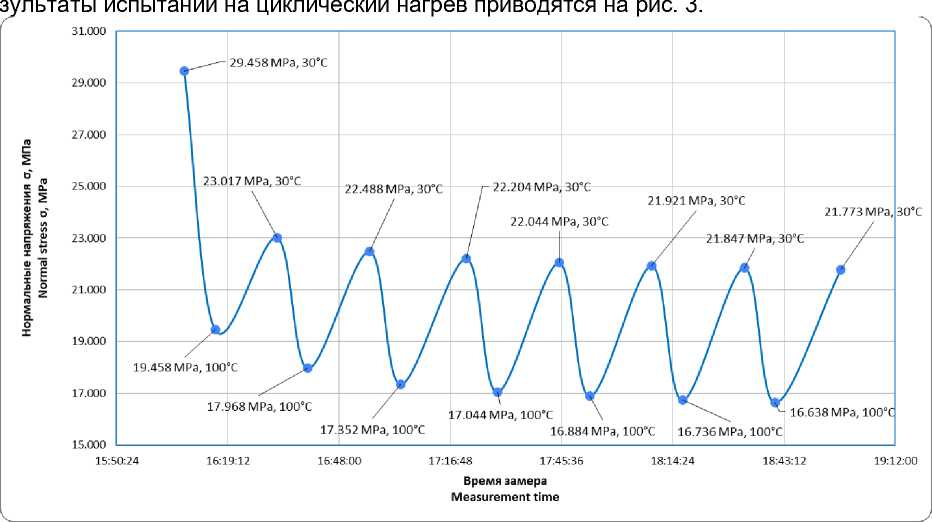
Рис. 3 – Результаты испытаний стеклопластика на циклический нагрев

Fig. 3 – FRP’s cyclic heating tests results

После каждого цикла нагрева-остужения напряжения в образцах не возвращаются в исходные значения. Постепенное снижение амплитудных значений складывается из накопления температурных сжимающих усилий и релаксации растягивающих. Подробный анализ работы материала и определение соотношения между релаксацией и накоплением температурных напряжений – направление дальнейших исследований. На данный момент сделано предположение, что резкое падение напряжений сразу после 1 цикла связано с “заморозкой”

температурных напряжений, а дальнейшее медленное снижение амплитудных значений – с постепенной релаксацией.

Косвенно это можно проверить путем оценки величины температурных напряжений по известной формуле:

a t = a E t Д t

Где a - коэффициент линейного температурного расширения (КЛТР), E_t - модуль упругости при температуре t,

Д t - изменение температуры.

Для нашего случая модуль упругости стеклопластика при повышенных температурах определяется из известного из предыдущих исследований [9] отношения t , где E – модуль E25         t упругости при температуре t, E25 - начальный модуль упругости при температуре 25°C (E25 » E30 ). Ранее было получено, что до 100°C включительно у композита падение жесткости не более 10%, после чего, при приближении к температуре стеклования связующего, происходит резкое E падение. В данном оценочном расчете примем —— = 0.9.

E 30

КЛТР также принимаем по [9], a = 11 - 10 6^

Тогда температурные напряжения составят:

a t = 11 - 10 ^{- 6} - 0.9 - 10006 - 70 = 6.93 МПа

Напряжения о- ₁₀₀ при повышенной температуре можно определить по следующей формуле:

^a 100 = -?" ^a 30 - ^a t

E 30

Где а з0 - изначальные напряжения перед нагревом. То есть, формула (4) учитывает снижение растягивающих напряжений из-за падения жесткости (деформация постоянная, следовательно, падают напряжения), а также добавление сжимающих напряжений от нагрева защемленного стержня.

a ₁₀₀ = 0.9 - 29.458 - 6.93 = 19.58 МПа

Напряжение а 100 = 19.58 МПа близко к экспериментальному значению в середине первого цикла (разница 0.62%). Считая, что все температурные напряжения были “заморожены” и остались в образце, оценим значение напряжений в конце первого цикла:

° 30,2 = ° 30 ^- ° t

° ₃₀,₂ = 29.45 8 - 6.93 = 22.53 МПа

Сходимость с экспериментом довольно близка (разница 2.1%).

На последующих циклах формулы (4–7) перестают работать. В результате эксперимента установлено, что напряжения после первого и последнего циклов отличаются на 15%. Это связано с тем, что новые температурные напряжения поверх накопленных не появляются, и за дальнейшие изменения отвечает релаксация. То есть, растягивающее усилие (верхние точки графика) снижается, и нижние точки также падают вслед за ним, т.к. температурные напряжения либо постоянны, либо релаксируют медленнее растягивающих (т.к. они ниже).

Таким образом, на данном этапе принимается предпосылка о том, что температурные напряжения в полном объеме “замораживаются” после первого цикла нагрева-охлаждения.

В результате постепенно происходит сдвиг в сторону сжимающих напряжений. Они наиболее опасны для тонкостенных оболочек, т.к. при превышении критических значений приводят к потере устойчивости. Это усугубляется тем, что при нагреве значительно падает жесткость конструкции. По полученным результатам сделан вывод, что даже разовое нарушение температурного режима может привести к возникновению и сохранению остаточных температурных напряжений, суммирующихся с действующими в конструкции. К примеру, при перегреве на 10°C температурные напряжения растут на 15%, а на 20°C – на 30%.

В цилиндрических и конических оболочках газоотводящих сооружений эффект возникновения и накопления напряжений возможен в кольцевом направлении, т.к. материал находится в стесненных условиях (за счет холодной внешней стороны оболочки, либо внешней обшивки в сэндвичевых оболочках).

Учитывая, что зачастую температурные напряжения основные по величине в такого рода конструкциях, при воздействии расчетных нагрузок это может в итоге привести к исчерпанию несущей способности. Помимо нарушений условий эксплуатации, аналогичный эффект может быть при разрушении защитного футеровочного слоя (изменение теплопроводности по толщине оболочки), например, от старения или абразивного износа, а также в результате горячего отверждения при изготовлении.

Чтобы продемонстрировать эффект возможного влияния накопления температурных напряжений, проведен расчет дымовой трубы при действии ветровой и температурной нагрузки. В программном комплексе ANSYS Workbench создана КЭ-модель конической дымовой трубы высотой 70 м, диаметром 4–6 м, с толщиной обшивок 12 мм и изоляционным слоем 100 мм (рис. 4). Толщина подобрана из условия обеспечения нормативного отклонения верха трубы по российским нормам [32].

0,000                        15.000                        30,000 (m)

7.500                        22.500

Рис. 4 – КЭ-модель трубы

Fig. 4 – Finite element model of the chimney

Ветровая нагрузка определена в соответствии с [33], а температура снаружи по теплотехническому расчету и требованиям нормативных документов [32], [34] и принята 60°C. Эксплуатационная температура отводимых газов 100°C.

Из рис. 5 можно видеть, что в кольцевом направлении во внутренней обшивке на самом деле возникают температурные сжимающие напряжения вплоть до 14.4 МПа в зоне краевого эффекта у опоры.

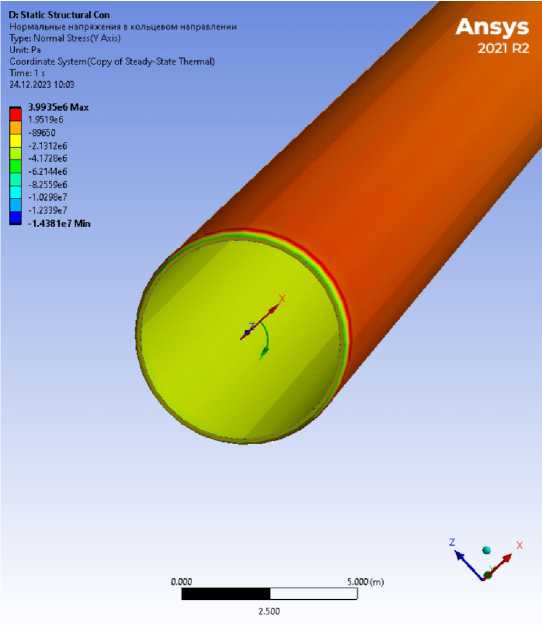
Рис. 5 – Кольцевые напряжения от температурных нагрузок Fig. 5 – Circumferential temperature stress

Были просчитаны кольцевые температурные напряжения при разных температурах. Было обнаружено, что из-за резкого падения жесткости после 110-120°C они начинают снижаться (рис. 6). Таким образом, для возникновения наихудшего случая может быть достаточно нарушения температурного режима на 10-20°C.

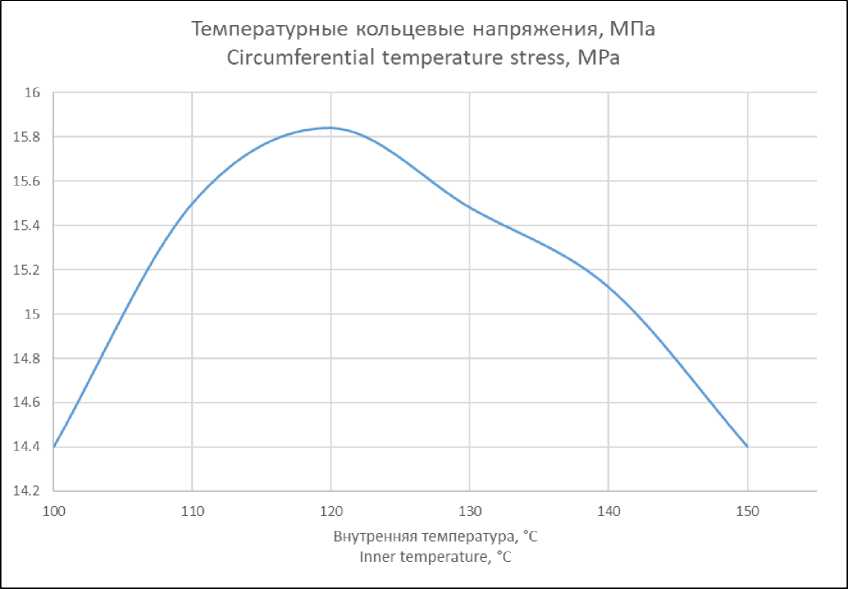
Рис. 6 – Температурные кольцевые напряжения

Fig. 6 – Circumferential temperature stress

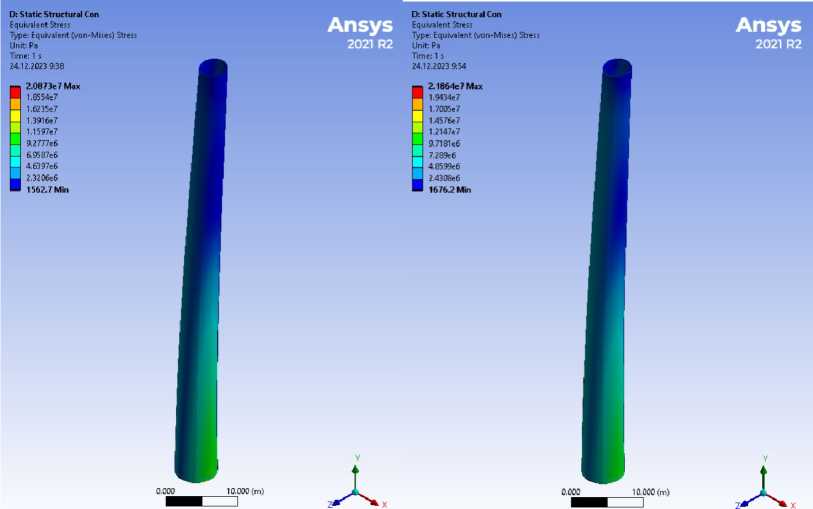
Без учета накопления напряжений их величина составила 14.4 МПа. При учете – 15.9 МПа. Таким образом, учет данного возможного эффекта повышает расчетные значения на ≈ 10%. Величина приведенных напряжений в трубе при одновременном действии ветра и температуры отличается на 5% (рис. 7).

5.000                                                                                                              5,000

Рис. 7 – Эквивалентные напряжения без учета накопления температурных (слева) и с учетом (справа)

Fig. 7 – Equivalent stress without considering the accumulation of temperature stress (on the left) and with it (on the right)