Наноструктура матриц серных строительных композитов: методология, методы, инструментарий

( к содержанию тальных исследований структуры и свойств наномодифицированных серных строительных композитов основным методом эмпирического исследования структуры на атомно-молекулярном уровне являлась спектроскопия комбинационного рассеяния; в качестве методов, результаты которых допускают кросс-верификацию, использованы методы квантовой химии и молекулярной динамики. Выполнен сравнительный анализ спектров технической серы и контрольного образца орторомбической серы; показано, что изгибные колебания звеньев S–S–S в технической сере происходят в менее стесненных условиях. Выполнен сравнительный анализ экспериментально найденных и расчетных значений комбинационного сдвига для изолированной молекулы циклооктасеры и элементарной ячейки орторомбического аллотропа. Показано существенное отличие значений комбинационного сдвига изолированной молекулы, соответствующих высокоэнергетическим модам, от значений для ячейки кристаллической решетки. Выявлено соответствие значений комбинационного сдвига для ячейки кристаллической решетки экспериментальным данным. Данное соответствие является весомым аргументом в пользу справедливости выбранной геометрической модели молекулярного кристалла серы. Показано, что методы молекулярной динамики, успешно применяющиеся на пространственных масштабах от 10 нм и выше, на нижнем пространственном масштабе для получения адекватных результатов должны быть дополнены квантово-механическими представлениями.

бъективной необходимостью повышения показателей эксплуатационных свойств материалов общестроительного и специ ального назначения, снижения эксплуатационных расходов, расходов на возведение и ремонт строительных конструкций, увеличения длительности межремонтного цикла, уменьшения материалоемкости строительства, исключения или смягчения отрицательных воздействий на окружающую среду, а также многими другими частными задачами гражданского и специального строительства обусловлена актуальность разработки новых высокоэффективных строительных материалов.

Структура и свойства строительного композиционного материала существенно зависят от вида матричного материала (вяжущего). Клас-

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

сификация строительных композитов по видам вяжущих является одной из основных; особое место в этой классификации занимают строительные материалы на серном вяжущем. Практически универсальная стойкость к воздействию влаги, водных растворов солей, кислот и оснований, малая величина открытой пористости, морозостойкость, отсутствие необходимости кардинальной модернизации существующих технологических линий – эти и другие характерные для многих серных материалов особенности делают их весьма привлекательными для строительства. Материалы на основе матриц, модифицированных серой, также находят многочисленные применения; в частности, использование модифицированных серой асфальтобетонов [1, 2] позволяет упростить технологию изготовления дорожных покрытий, повысить показатели эксплуатационных свойств (в т.ч. пределы прочности и стойкость дорожной одежды к колееобразованию). В конечном итоге это приводит к снижению затрат на изготовление и эксплуатацию дорожной одежды, а также уменьшает нагрузку на окружающую среду вблизи предприятий нефтегазовой отрасли за счет ликвидации отвалов серы [2].

По сравнению с другими видами матричных материалов техническая сера обладает целым рядом преимуществ, в числе которых дешевизна и возможность эффективного управления процессом структуро-образования посредством изменения теплового режима изготовления строительных изделий и конструкций [3].

В процессе создания серных строительных материалов различного назначения были разработаны многочисленные рецептурно-технологические методы повышения показателей свойств. Таким методом, в частности, является нанесение на поверхность тонкодисперсной фазы микроструктуры серного композита высокомолекулярных веществ – прекурсоров [4, 5]. При этом слой прекурсора и обусловленный его наличием переходной слой на поверхности частиц наполнителя имеют, как правило, нанометровый размер [3, 4]. В то же время, во многих случаях надмолекулярная структура сформированных подобным образом переходных слоев остается неизвестной [6].

Несмотря на достигнутые в последние десятилетия значительные успехи в исследовании аллотропов серы, структуры и свойств серосодержащих материалов [7, 8], материаловедение серных композитов нельзя рассматривать как завершенную область строительного материаловедения. В частности, детального исследования требуют структура

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

и свойства серного вяжущего вблизи межфазных границ дисперсно-наполненных наномодифицированных серных композитов. Последнее, в свою очередь, требует наличия прочного теоретико-эмпирического основания – достоверных сведений о структуре и свойствах вяжущего. Не подлежит сомнению, что значительный объем знаний уже накоплен – детальные исследования молекулярной структуры аллотропов серы датированы началом XX столетия [9], при этом результаты исследований – кристаллографические данные в форме, допускающей использование при выполнении модельных экспериментов – являются доступными [10] для широкого круга исследователей.

Перечень направлений, так или иначе связанных со структурой и свойствами серного вяжущего, включает исследование атомно-молекулярной структуры различных аллотропов серы [11–13], исследование свойств изолированных молекул Sn, а также изучение структуры и свойств серосодержащих веществ [7, 8].

Накопленный к настоящему времени объем теоретико-практических знаний становится частью эффективного инструментария материаловеда, использующего в практике разработки достижения интегративной дисциплины – системного анализа [5, 14, 15].

Необходимые условия успешного применения системного анализа в строительном материаловедении к настоящему времени определены. Иерархическая декомпозиция [5, 14] строительного материала как сложной системы по моделям, процессам и фазам возможна, если определен тип доминирующего взаимодействия или класс физико-химических эффектов, оказывающих существенное влияние на структурообра-зование и в конечном итоге определяющих множество эффективных на данном структурном уровне методов исследования.

На уровне наноструктуры строительного композита – структурного уровня проявления размерных эффектов [15] – для исследования процессов и оценки параметров структурообразования, исследования влияния рецептурно-технологических параметров на свойства материала, вместе с экспериментальными методами исследования могут применяться методы квантовой химии и молекулярной динамики. При этом методология исследования наноструктуры как подход к выполнению исследования в целом определяется не только потребностями практики (которые, собственно, и заключаются в создании строительного материала с требуемым комплексом показателей эксплуатационных свойств), но и зависит также от предельно допустимых затрат времени и материальных ресурсов, требований в отношении точности и воcпроизводимости результатов, необходимости получения новых теоретико-эмпирических сведений с высоким прогностическим потенциалом (рис. 1–3).

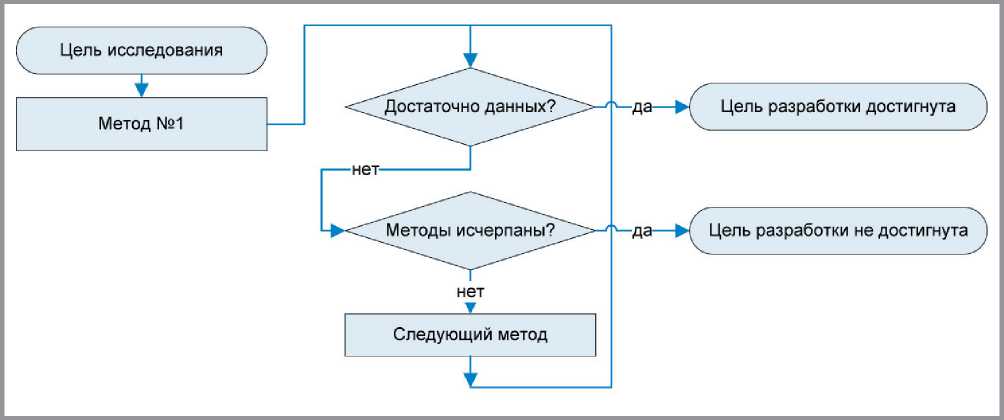
Рис. 1. Общая схема изучения наноструктуры в случае доминирующей значимости практической составляющей исследования

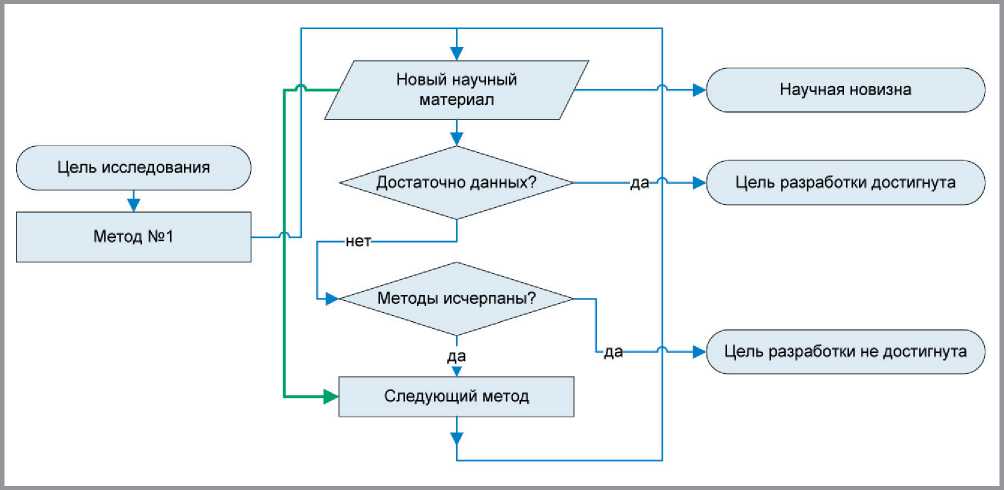
Рис. 2. Общая схема изучения наноструктуры в случае повышенной значимости научной составляющей исследования

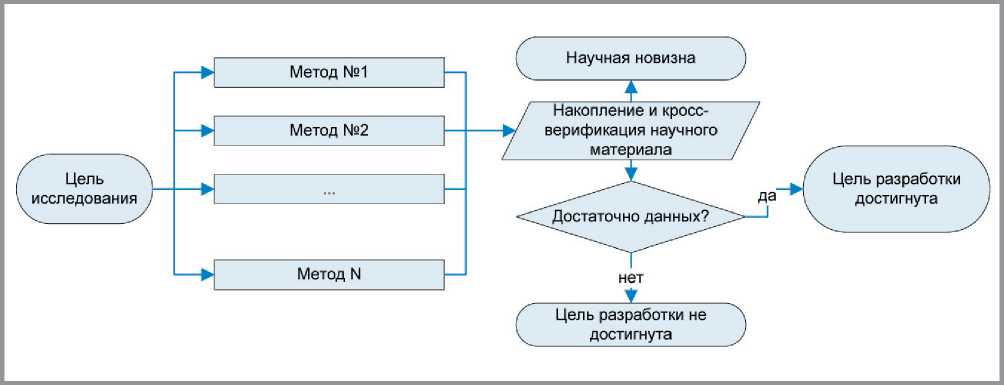
Рис. 3. Общая схема изучения наноструктуры в случае повышенных требований к времени выполнения, точности, достоверности и воспроизводимости

Схема исследования, приведенная на рис. 1, наиболее проста: исследование ведется до момента достижения практической цели или до исчерпания доступных методов исследования (рецептурно-технологических приемов и методик наномодификации). Результаты, полученные на промежуточном шаге (не приводящем к достижению цели – практического результата), не используются на последующих стадиях, выполняемых с привлечением других методов исследования. Очевидно, что использование схемы на рис. 1 для исследования, направленного на достижение практического результата, приведет к снижению затрат времени и материальных ресурсов в том случае, если методы отсортированы по уменьшению практической пригодности. Если практическая пригодность априори неизвестна, то на первый план выходит основной недостаток схемы: потеря информации, полученной на предыдущих этапах исследования.

Указанный недостаток не имеет места для схемы на рис. 2, которую от рассмотренной ранее схемы отличает наличие дополнительного информационного блока и, возможно, механизма использования теоретико-эмпирической информации, полученной на предыдущих этапах исследования (соответствующее направление передачи информации на рис. 2 отмечено зеленой линией). Упорядочение методов по критерию практической пригодности для схемы на рис. 2 определяет баланс между «научным» и «практическим» выходом исследования; наихудший ( к содержанию

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

с практической точки зрения выбор порядка при прочих равных условиях приводит к получению наибольшего объема новых теоретико-эмпирических данных об объекте исследования. Такая схема применима и в случае нижнего ограничения на указанный объем (квалификационные и отчетные исследования).

Обе рассмотренные схемы представлены как последовательный научный поиск. Основной недостаток схемы на рис. 1 становится ее положительной стороной (отсутствие зависимости по данным) в том случае, если исследования необходимо выполнять параллельно; наличие N методов и M параллельных процессов исследования обуславливает в среднем снижение затрат времени при повышении затрат материальных ресурсов (в предположении об оптимальной с практической точки зрения сортировке методов). Эта особенность параллельной реализации, в зависимости от целей и ресурсных ограничений, может оказаться и положительной, и отрицательной ее стороной.

Препятствующую параллельной реализации схемы на рис. 2 зависимость по данным можно исключить. Негативное влияние этого действия (снижение прогностической способности всего исследования в терминах строительного материаловедения), помимо возможности параллельной реализации, дополнительно компенсируется возможностью выполнения взаимной верификации результатов, полученных с использованием различных методов исследования (рис. 3).

Приведенные на рис. 1–3 схемы являются идеализированными; реальное исследование обычно включает элементы каждой из них. Использование некоторых методов исследования (как экспериментальных, так и теоретических – ИК- и комбинационная спектроскопия, ЯМР-спектроскопия, адсорбционная порометрия, рентгеновская дифрактометрия, основанные на теории функционала плотности методы квантовой химии) приводит к получению большого массива данных, полное использование которых в рамках ориентированного на решение задач практики исследования не представляется возможным. Результаты, полученные с использованием подобных методов, обычно и составляют материал для взаимной верификации. Использование других методов (механические испытания, реологические исследования макроструктуры, рентгеновское рассеяние, основанные на моделях статистической физики численные эксперименты) приводит к получению скалярных значений; сами методы оптимальны для решения практи-

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

ческих задач, а полученные скалярные значения показателей (как правило, макроскопических свойств материала) могут являться предметом «однонаправленной» верификации.

В материаловедении дополнительную сложность в схему реального исследования вносит наличие большого числа способов кроссверификации и возможных сочетаний методов, множества типов результатов которых имеют непустое пересечение.

Например, результаты натурного исследования спектра комбинационного рассеяния допускают верификацию результатами численных исследований, проведенных как с привлечением теории функционала плотности (ТФП), так и с привлечением методов молекулярной динамики. При этом в случае ТФП возможно использование различных базисов и типов самосогласованного поля; в случае молекулярной динамики обычно имеется определенная свобода выбора (неопределенность) в отношении выбора потенциала (силового поля).

В то же время, многие методы позволяют получить результаты, пригодные для верификации не единственного другого метода; так, численные эксперименты с моделями ТФП или молекулярной динамики могут быть использованы не только для верификации спектров комбинационного рассеяния, но и для верификации результатов ИК-спектроскопии, а также для прогностических суждений в отношении макроскопических характеристик строительных материалов [16, 17].

Верификация численных алгоритмов и их реализаций (корректность программного обеспечения) лежит уже вне материаловедения. Тем не менее, на практике совместное использование различных алгоритмов и их реализаций может оказаться полезным с точки зрения повышения достоверности полученных результатов.

Следует также отметить, что фигурирующее на рис. 1–3 разделение научных знаний и практических результатов, являясь объективным, обуславливает возможность инверсии в этой паре; часть выводов при этом проявляет себя в качестве инвариантов, другая часть может подвергнуться инверсии в отношении субъекта, предиката или квантора (в случае схемы на рис. 2: «наилучший метод для получения научных знаний – это метод, в последнюю очередь приводящий к получению практического результата»).

Схема на рис. 3 по большинству существенных свойств является наилучшей. Попытка выполнить исследование в соответствии с этой

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

схемой может быть удачной (это имеет место, как правило, начиная с некоторого объема априорной информации), или же по завершению исследования приходится констатировать неявный переход к («диссертационной») схеме на рис. 2. Изложенное ниже содержание, имеющее самостоятельное значение с точки зрения развития материаловедения серных строительных композитов, можно рассматривать и как иллюстрацию последнего утверждения.

На предварительной стадии теоретико-экспериментальных исследований структуры и свойств наномодифицированных серных строительных композитов выполнялось накопление фактического теоретико-эмпирического материала; основным методом эмпирического исследования структуры на атомно-молекулярном уровне являлась спектроскопия комбинационного рассеяния. Выбор метода в первую очередь оправдывается высокой комбинационной активностью аллотропов серы (см. рис. 6 – контрольные комбинационные спектры серного вяжущего). Параллельно (схема рис. 3) с натурным экспериментом выполнялись численные исследования; их выбор сделан в соответствии с отмеченным в [15] положением о практической пригодности методов, используемых на «соседних» по отношению к наноструктуре масштабных уровнях (ТФП, молекулярная динамика). В ходе численных исследований использовались различные программные реализации.

Множество методов составляют:

• 1.    Спектроскопия комбинационного рассеяния.

• 2.    Численные методы моделирования, привлекающие модель самосогласованного поля [18].

• 3.    ТФП с обобщенной градиентной аппроксимацией [19].

При выполнении численных экспериментов использовались:

• 1.    Квантово-химический пакет DMol³ [20].

• 2.    Квантово-химический пакет CASTEP [21].

• 3.    Квантово-химический пакет GAMESS [22].

• 4.    Авторское программное обеспечение молекулярно-динамического моделирования [23, 24].

Вместе с пакетом квантово-химического моделирования [22] использованы различные инструменты пре- и постпроцессинга [25–28].

Базу для кросс-верификации составили данные, полученные в ходе натурных и численных экспериментов. Конечная цель кроссверификации – суждения о практической пригодности метода и до-

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

стоверности результатов; наряду с указанным суждением в результате кросс-верификации часто удается сформулировать суждения и в терминах материаловедения.

Результат экспериментального исследования спектров комбинационного рассеяния образца технической серы (рис. 4) и контрольного образца кристаллической серы (рис. 5) представлен на рис. 6.

Рис. 4. Образец технической серы

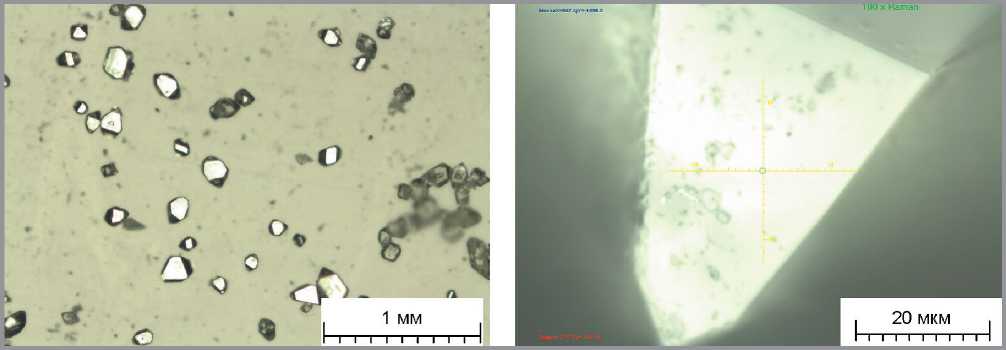
Рис. 5. Образцы кристаллической серы, используемые в качестве контрольных при исследовании влияния наномодификации на атомно-молекулярную структуру вяжущего

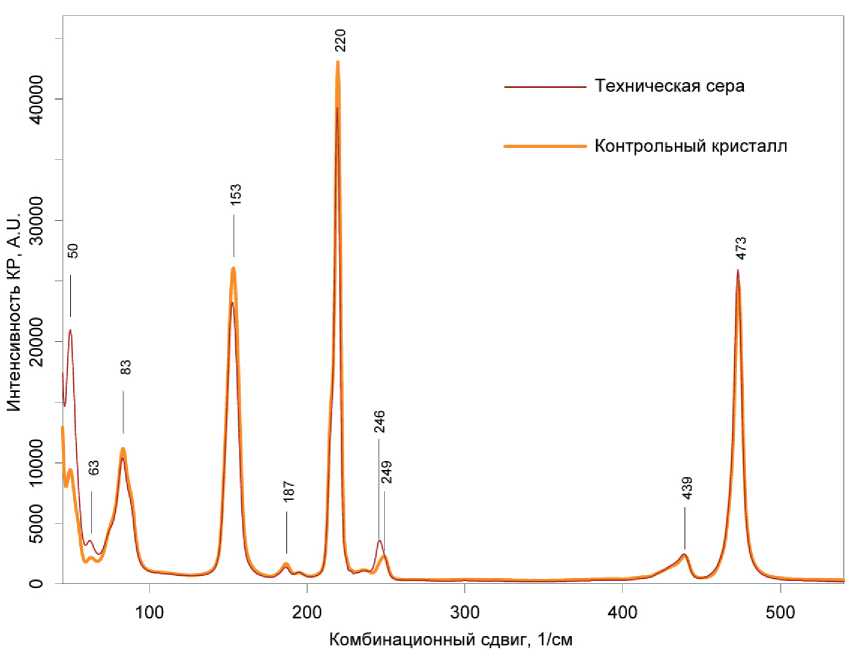
Рис. 6. Спектры комбинационного рассеяния технической серы и контрольного кристалла

Показанные на рис. 5 образцы выращены из насыщенного раствора серы в толуоле. Время выращивания 30 мин, скорость испарения растворителя 0,1 см3/мин. Спектр комбинационного рассеяния получен на конфокальном спектрометре SENTERRA при следующих параметрах схемы регистрации: температура 300 K, длина волны излучения возбуждения 532 нм, мощность излучения возбуждения 0,2 мВт, разрешение 3 см–1, время накопления 60 с, апертура 50 мкм.

Как следует из рис. 6, спектры комбинационного рассеяния технической серы и контрольного образца кристаллической серы практически идентичны. При этом на спектре контрольного образца отсутствуют линии растворителя (толуол легко идентифицируется по спектру комбинационного рассеяния; одной из интенсивных является линия вблизи 510 см–1), что позволяет сделать вывод о полном его удалении из контрольного образца орторомбической серы. В целом, спектры на рис. 6 очень точно соответствуют литературным данным. Незначительные отличия в спектрах технической серы и контрольного образца имеют место. Линия технической серы вблизи 50 см–1, соответствующая фундаментальной колебательной моде ag [29], имеет повышенную относительную интенсивность. Комбинационный сдвиг для линий вблизи 250 см–1 также заметно меняется. Линия 250 см–1 соответствует изгиб-ным колебаниям звена S–S–S. Для технической серы эта линия смещена в сторону меньших частот (меньших энергий). На этой основе можно сделать вывод о том, что изгибные колебания звеньев S–S–S в образце технической серы имеют место в менее стесненных условиях.

К настоящему времени разработано большое число программных пакетов квантово-химического анализа. Некоторые пакеты [20, 21] являются программными продуктами с закрытым исходным текстом и распространяются на коммерческой основе; с ними сосуществуют некоммерческие пакеты (например, [22]) с открытым исходным текстом.

Квантово-химические пакеты DMol3 и CASTEP распространяются в составе интегрированной среды вычислительного материаловедения BIOVIA Materials Studio. Данная интегрированная среда позиционируется как передовой инструмент разработки материалов (в т.ч. строительных). Наряду с модулями DMol3 и CASTEP в состав интегрированной среды включены модули для численного анализа методами молекулярной динамики и многие другие инструменты, в частности – средства визуализации, подготовки расчетных заданий и постобработки (рис. 7). Очевидным «недостатком» является цена лицензии (при включении всех модулей – десятки тысяч евро).

Как правило, пакеты научного программного обеспечения с открытым исходным кодом (в т.ч. использованные в настоящей работе [22, 23]) разрабатываются в соответствии с «философией UNIX Way» – пакет реализует ту и только ту задачу, для которой он создавался (например, алгоритмы ТФП или молекулярной динамики). Для решения сопутствующих задач исследователь должен привлекать дополнительные программные инструменты.

Пакет GAMESS [22] реализует только алгоритмы квантовой химии. Этот пакет представляет собой инструмент, управляющийся параметрами командной строки и требующий в качестве входных данных сформированный по определенным правилам текстовый файл. Задачи

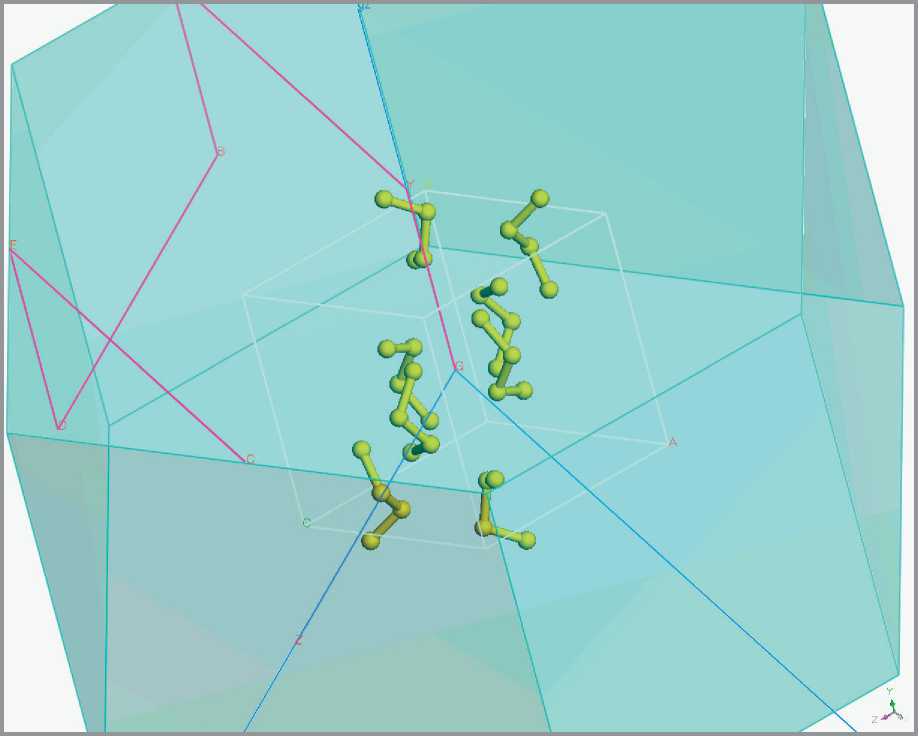
Рис. 7. Визуализация кристалла орторомбической серы в среде BIOVIA Materials Studio подготовки квантово-химического расчета и постобработки должны решаться другими программными пакетами. Недостатки и достоинства подобной модульности – предмет длительных и часто бессодержательных дискуссий; этот подход де-факто является стандартом в научных численных экспериментах.

Выбор средств для подготовки и постобработки расчетного задания – во многом вопрос предпочтений; в то же время известно минимальное множество средств с достаточными для практических применений возможностями. Инструменты [25–28] являются свободно распространяемыми некоммерческими пакетами с открытым исходным текстом и могут успешно применяться в повседневных задачах квантово-химических исследований, возникающих в практике нанотехнологии строительного материаловедения.

Инструмент Jmol [25] может быть использован только для визуализации (рис. 8) атомно-молекулярных структур (в состав инструмента входит реализация алгоритма локальной минимизации энергии, применимая для предварительной оптимизации геометрии; однако без средств визуального молекулярного дизайна преимущество наличия этой реализации не очевидно).

Пакет молекулярной графики PyMOL [26] также предназначен для решения задач визуализации (рис. 9). Функциональные возможности пакета в части визуализации существенно превышают таковые для пакета Jmol – интерактивная и пакетная визуализация, анимация. Пакет позволяет получать детальные изображения сложных атомно-молекулярных структур с типографским качеством и часто используется в качестве инструмента для оформления журналов, издаваемых Nature Publishing Group .

Как для визуализации, так и для подготовки расчетных квантово-химических заданий могут быть использованы пакеты Gabedit [27] и Avogadro [28]. Эти пакеты, в частности, содержат средства генерации входного файла GAMESS (рис. 10, 11).

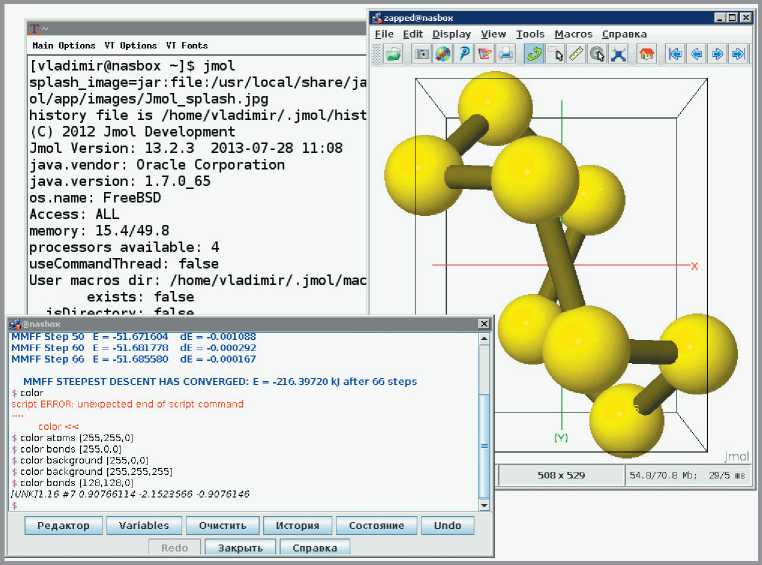
Рис. 8. Пакет Jmol: визуализация изолированной молекулы циклооктасеры

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

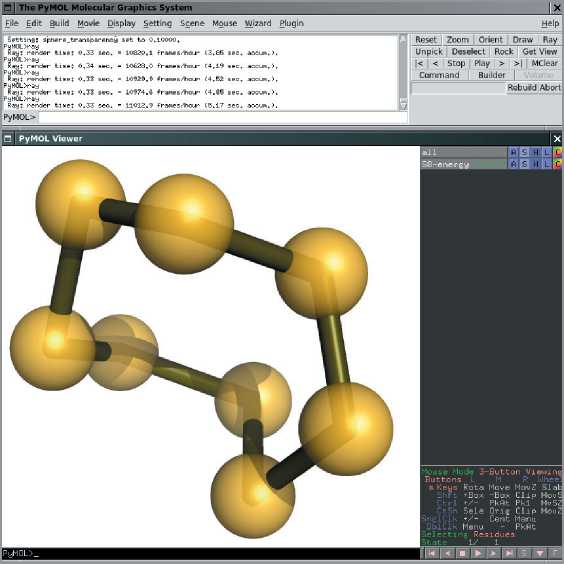
Рис. 9. Консоль и главное окно PyMOL с растровым образом, полученным методом трассирования луча

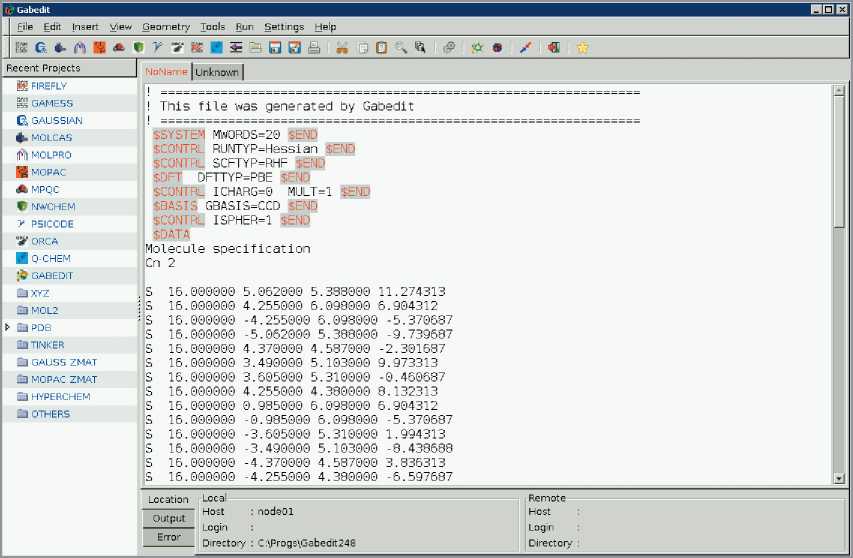
Рис. 10. Главное окно пакета Gabedit с расчетным заданием для GAMESS

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

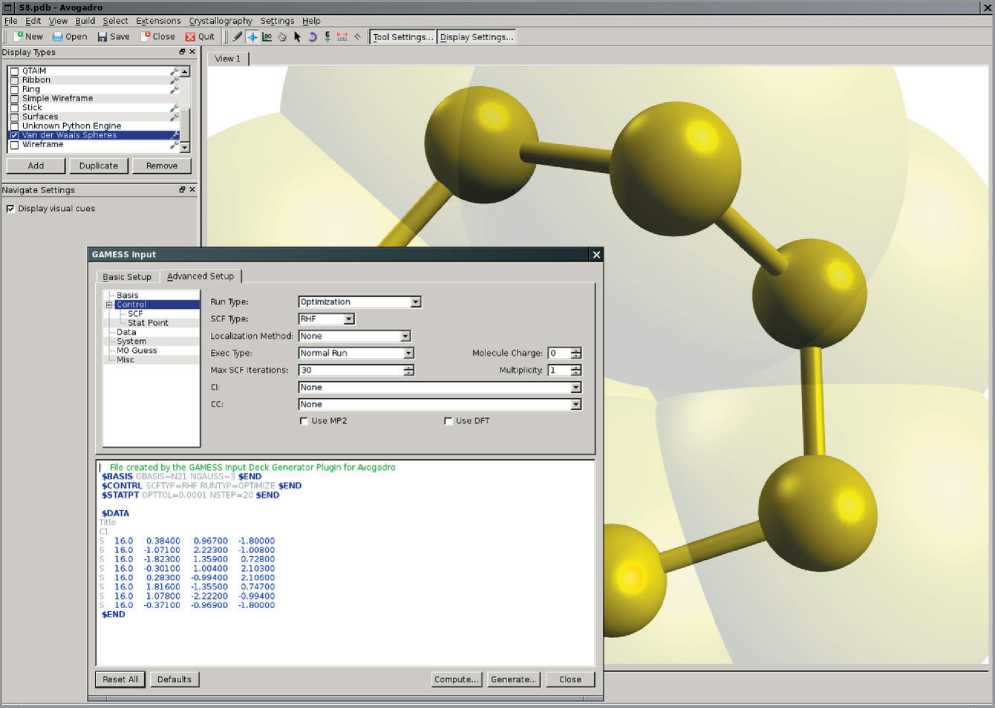
Рис. 11. Главное окно (интерактивная визуализация) и диалог подготовки расчетного задания для GAMESS в пакете Avogadro

Численное нахождение спектров комбинационного рассеяния (в особенности – спектров периодических структур и структур с симметриями), независимо от стоимости лицензии используемого квантово-химического пакета, представляет собой нетривиальную задачу; это связано с уровнем теории, обеспечивающей модели для расчетных алгоритмов квантовой химии.

На практике для численного нахождения спектров комбинационного рассеяния (непериодических) атомно-молекулярных структур с использованием пакета GAMESS необходимо выполнить три стадии расчетов. Если геометрия системы была определена средствами интерактивного моделирования, то первой стадией является оптимизация геометрии по критерию минимума энергии (управляющий параметр GAMESS «RUNTYP=Optimize»). Следующая стадия числен-

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^e 121 ( к содержанию2)

ного анализа – модельный (частотный) анализ и нахождение энергетических характеристик молекулы (управляющий параметр GAMESS «RUNTYP=Hessian»). Нахождение спектра комбинационного рассеяния выполняется на третьей стадии (управляющий параметр GAMESS «RUNTYP=Raman»), расчетное задание для которой включает найденные на второй стадии энергетические параметры (матрица «$HESS» выходного файла).

Результаты вычисления активности комбинационного рассеяния (этот параметр, в отличие от интенсивности, не зависит ни от температуры измерения, ни от длины излучения возбуждения) для изолированной молекулы циклооктасеры (DM, GAMESS) и ячейки орторомбического аллотропа (CAS) приведены в табл. 1. Интенсивности, соответствующие второму столбцу табл. 1, иллюстрируются рис. 12.

Таблица 1

Активность комбинационного рассеяния изолированной молекулы S8 и элементарной ячейки орторомбического аллотропа

Мода, п/п	DM		GAMESS		CAS		Experimental
	Частота, см–1	Активность, A.U.	Частота, см–1	Активность, A.U.	Частота, см–1	Активность, A.U.	Частота, см–1	Активность, A.U.
1			50,98	8710	51,47	9643	50,00	8883
2	63,10	5046	64,00	5760	60,45	3574	65,00	2017
3	83,40	3757	80,98	3710	85,14	4587	83,00	10980
4	142,70	13786	142,60	13580	–	–	–	–
5	157,40	6523	156,54	10780	154,89	15794	153,00	26022
6	171,00	15246	172,87	9810
7	190,60	2752	191,61	3970	192,45	4975	187,00	1370
8	224,50	4630	224,73	18380	224,89	17683	220,00	43040
9	267,90	5911	265,31	8880	258,11	6749	250,00	2047
10	362,60	3863	360,15	11980
11	420,20	3580	423,52	17530
13	443,20	27736	444,10	33840	445,67	7918	439,00	2191
14	461,20	22116	463,18	28450	471,27	25948	473,00	24862

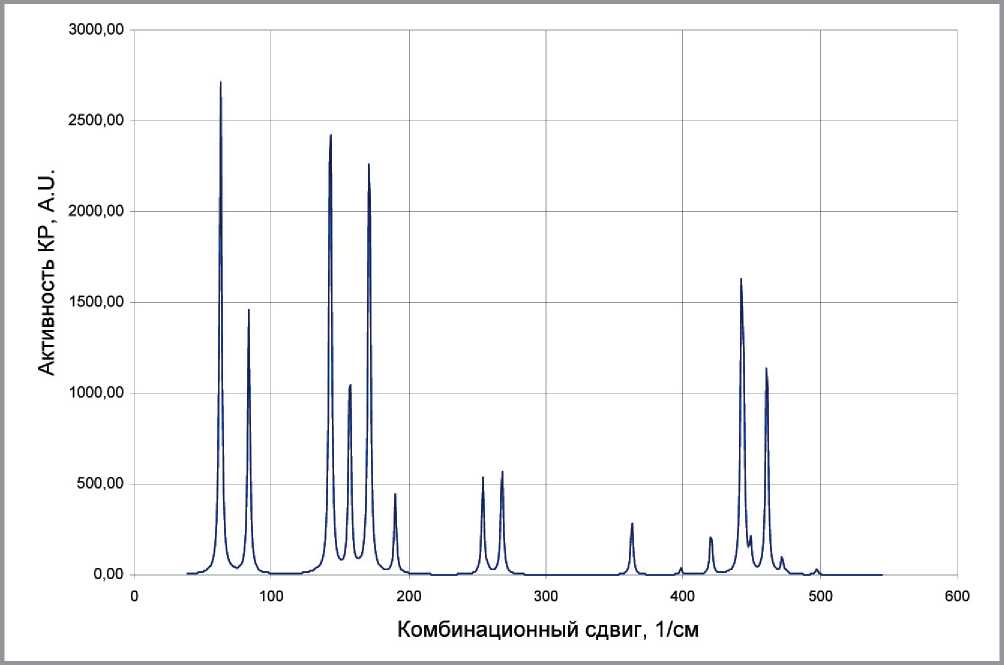
Рис. 12. Комбинационная активность изолированной молекулы S₈

Как следует из табл. 1 и рис. 12, значения комбинационного сдвига изолированной молекулы циклооктасеры в целом весьма существенно отличаются как от значений для элементарной ячейки орторомбического аллотропа, так и от результатов экспериментальных исследований. Найденные численно значения комбинационного сдвига изолированной молекулы близки к значениям для кристалла только в области малых энергий (моды с частотами 50, 65 и 80 см–1). Моды 4, 6, 10 и 11 или не соответствуют каким-либо степеням свободы кристаллической структуры серы, или не являются комбинационно-активными. Интенсивности мод (рис. 12), найденные на основе данных для изолированной молекулы по табл. 1, не соответствуют экспериментально наблюдаемым (рис. 6). Результаты численного отыскания спектра комбинационного рассеяния элементарной ячейки орторомбического аллотропа в целом хорошо соответствуют экспериментальным данным в части значений комбинационного сдвига (столбцы 5 и 6 табл. 1). Соответствие теоре-

Е.В. КОРОЛЕВ и др. Наноструктура матриц серных строительных композитов...

тических результатов, полученных методами квантовой химии, экспериментальным результатам исследования спектров комбинационного рассеяния является весомым аргументом в пользу справедливости выбранной геометрической модели молекулярного кристалла серы.

По отношению к уровню наноструктуры методы квантовой химии являются методами «нижнего», атомно-молекулярного масштабного уровня; их успешное использование в рассмотренном случае обусловлено тем, что они были использованы для исследования элементарной ячейки молекулярного кристалла (пространственный масштаб, соответствующий нижней границе наноструктуры), при котором вычислительная сложность методов квантовой химии еще не выходит за допустимые рамки. Методы молекулярной динамики обычно применяются для исследования систем с размерами от десятков нанометров; в то же время, принципиальное ограничение на их использование в рассмотренной задаче также отсутствует.

И для численного решения уравнений движения, и для визуализации моделируемой системы нами использовано программное обеспечение [23]. Алгоритм моделирования обсуждался, в частности, в работе [24].

Сведения из термодинамики позволяют оценить [30] параметры в выражении потенциала парного взаимодействия; использован потенциал Леннард–Джонса. Уравнение движения является чрезвычайно простым:

m_i Г i – k_i (Г i –v i ) = ∇ U i , i = 1,N ,                                             (1)

где mi , r _i = ( x_i,y_i,z_i ) – массы и координаты i -й частицы, k – диссипативный фактор, v _i – скорость среды в точке r _i , U_i – потенциал в точке r _i , N – число частиц.

Модель (1) может быть преобразована в систему 6 N обыкновенных дифференциальных уравнений первого порядка, после чего численно решается задача Коши. Для решения задачи Коши в [23] использован метод вложенных форм.

Результат моделирования эволюции на атомно-молекулярном уровне показан на рис. 13 и 14.

Программное обеспечение [23] ранее было успешно использовано для моделирования различных процессов на уровнях нано-, микро-

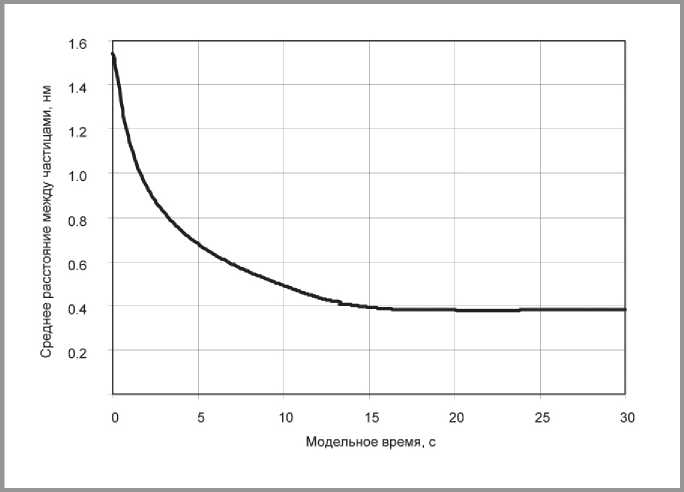
Рис. 13. Среднее расстояние между частицами

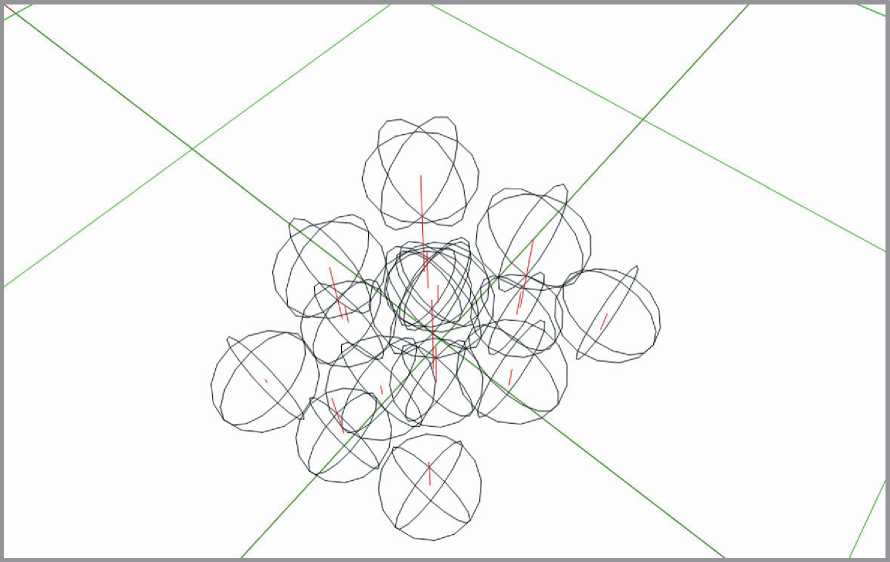
Рис. 14. Фрагмент установившейся пространственной конфигурации (сферы Ван-дер-Ваальса)

и макроструктуры строительных композитов. Результаты, полученные на пространственных масштабах от 10 нм и выше, находились в соответствии с экспериментальными данными.

В то же время, представленные на рис. 13 и 14 результаты свидетельствуют о неудовлетворительной адекватности использованных молекулярно-динамических методов на атомно-молекулярном уровне. Если квантово-механические эффекты не принимаются во внимание, то установившееся среднее значение межатомного расстояния примерно в два раза превышает действительное значение (и для изолированной молекулы S8, и для элементарной ячейки). Сферы с радиусом Ван-дер-Ваальса на рис. 14 не пересекаются между собой, что не должно иметь места для реальной конфигурации. Таким образом, методы молекулярной динамики могут успешно применяться на пространственных масштабах от 10 нм и выше; на нижнем пространственном масштабе для получения адекватных результатов требуется принимать во внимание квантово-механические эффекты.

У важаемые коллеги !

П ри использовании материала данной статьи просим делать библиографическую ссылку на неё :

D ear colleagues !

T he reference to this paper has the following citation format :