Напорное ламинарное течение броуновской суспензии в плоском канале

Броуновские суспензии относятся к коллоидным системам и наножидкостям [1], в которых частицы практически не седиментируют в осадок, т.к. броуновское движение препятствует этому и кроме того в них отсутствуют условия для коагуляции из-за их одинакового заряда. Гидродинамический анализ таких гетерогенных систем, как правило, осуществляется с позиций однофазного представления [2] с одновременным учетом внутренней структуры реологической формализацией. Тем не менее, двухфаз-ность броуновских суспензий может проявляться неожиданным образом, например, добавление пыли к воздуху при турбулентном его движении по трубопроводу заметно снижает коэффициент сопротивления [3]. В [4] установлено, что при рассмотрении ламинарного течения Куэтта броуновской суспензии в плоском горизонтальном канале трение для дисперсионной и дисперсной фаз уменьшается на обеих стенках канала. Это свидетельствует о том, что возможно возникновение гидродинамических неоднородностей таких как, например, в неброуновских суспензиях имеют место различающиеся по своей структуре поля скоростей фаз из-за миграционных эффектов. Для объяснения различия полей скоростей фаз при течении броуновских суспензий в [5] принимается допущение о седиментации твердых частиц.

В связи с этим необходимо исследовать поведение броуновских суспензий при их вынужденном ламинарном течении в плоском горизонтальном канале с целью идентификации закономерностей по влиянию дисперсной среды на гидродинамические характеристики [6].

1.    Математическая модель

Для анализа гидродинамических характеристик суспензий применяется двухфазный подход, основывающийся на траекторных и двухжидкостных модельных представлениях [7, 8], которые в современной интерпретации изложены в [9]. В траекторных моделях детали потока определяются либо путем отслеживания движения отдельных частиц, либо репрезентативного конгломерата дисперсной фазы [10]. В двухжидкостных моделях дисперсная фаза представляется другой непрерывной фазой, которая смешивается и взаимодействует со средой-носителем [11]. Для практических целей мониторинг отдельных частиц в потоке суспензии малопригоден при оценивании поведения гетерогенной системы в интегральном смысле, поэтому наиболее часто используется двухжидкостная модель [12, 13], которая для ламинарного потока броуновской суспензии без фазового перехода и осаждения частиц, в отсутствии массовых сил с ньютоновским реологическим законом непрерывных несжимаемых фаз трансформируется в уравнения [14–16]

v- U f,s = 0; (1)

dufs , .

a f,s p f,s —gf + a k p k (U f,s • V) U fs = -a f,_s Vp - Vp c +

+ ^a f,s ^ f,s ^V 2 u f,s + k ^{( u} s,f - ^U f,s ⁾ , ⁽²⁾ где нижние индексы f и s относятся соответственно к дисперсионной и дисперсной фазам; t – время; α f,s , µ f,s , ρ f ,s – локальная объемная доля, динамическая вязкость и плотность фаз; U fs - вектор скорости; p,p c — давление в несущей среде и частиц в уравнении для дисперсной фазы; k – коэффициент лобового сопротивления движению частиц; (a f,_s , p f,_s , p f,_s , k = const).

Ввиду пренебрежимо малой инерции частиц в суспензиях, их перемещения определяются с точностью до флуктуаций, обусловленных броуновским движением, которые становятся значительными при малых размерах самих частиц. Таким образом, дисперсная фаза связана с давлением частиц, которое компенсирует движение частиц, приводящее к изменению их объемно доли. В [17] показано, что давление частиц p пропорционально их энергии E _s , которая характеризует стабильность гомогенности суспензии из-за локального изменения объемной доли дисперсного потока, вызванного его сжимаемостью, тогда

∇ p c ≈ α s ρ s ∇ E s .

В [18] для разбавленных монодисперсных суспензий классифицированы следующие режимы на основе числа Стокса Stk = m | u _s — U f | / (6np f r ² ), где m - масса частицы с

Stk ≫ α s ^{- 3/2} определя-

радиусом r: распределение скоростей ≪массивных≫ частиц ется их столкновениями и гидродинамическим взаимодействием; для ≪мелких> ча- стиц Stk ≪ αs-3/2

столкновения частиц не играют никакой роли, и распределе- ние их скоростей полностью определяется гидродинамическим взаимодействием. Для энергии "мелких"частиц зафиксирована неоднородность в распределении их скоро- стей с лимитированием энергии частиц в поперечном направлении потоку, поэтому

E _s = Stk ^{- 2} / ³ | u _s — U f | ² I (36 п ) ^1/3 .

Из (3) и (4) следует соотношение для градиента давления частиц

Vp c =

α s ρ s ^√ 3 _π

( 9 p f V’ ³^

--- ^V | u s

\ 16 p _s rj

-

U f | ^4/3

которое после линеаризации ∇ [u s — Uf | ^4/3 в среднеквадратичном приближении в предположении, что флуктуации скорости скольжения не превосходят ε u ₀ , где

0 <ε< 1, u 0 – средняя скорость суспензии, приобретает окончательный вид

Vp c = a s p s 3(9 f / |V U s — VU f | .                 (5)

V п V⁶ Ps^rJ

Если к частицам не прикладывается внешний крутящий момент и рассматривается течение с низким числом Рейнольдса (ускорение и напряжения Рейнольдса незначительны), то в [19] показано, что для дисперсной фазы может быть выбрана структу- ра реологического закона, аналогичного для ньютоновской жидкости, причем в этом случае разность относительных (приведенных к вязкости несущей среды) вязкостей суспензии и дисперсной фазы равна 1. Это позволяет определить вязкость дисперсной фазы через вязкость ^sf суспензии, т.е. ^s = ^sf — ^f.

В [20] экспериментально показано, что при вынужденном ламинарном течении наножидкости (вода и наночастицы Al2 O3 и (или) CuO) с объемной долей частиц as< 0.01, сопротивление потоку броуновской суспензии действительно уменьшается в сравнении с потоком ≪чистой≫ дисперсионной среды. При этом агрегативная и

кинетическая устойчивость броуновской суспензии наблюдается при одновременном выполнении условий as< 0,01 и Pe =

< 10 [21], где p f - динамическая

6nr ³ ^ f ү kT

вязкость дисперсионной фазы; k – постоянная Больцмана; T – температура системы; Y - скорость деформации движущейся среды.

Рассмотрим плоский полуограниченный канал высотой 2h, по которому движется в ламинарном режиме агрегативно и кинетически устойчивая броуновская суспензия в декартовой 2-D системе координат (x, y – продольная и поперечная координаты) с началом на входной кромке нижней стенки канала. Из предположения об однонаправленности течения суспензии и 2-D геометрии, т.е. Uf,s = (ufs,Uf,s), компоненты Uf,s = Uf,s (х,У,т), Uf,s = Uf,s (x,y,T) и кроме того расход суспензии через любое поперченное сечение постоянен, так что вместо независимой переменной правомерно использовать x = uot, где u0 = const скорость потока суспензии на входе в канал, тогда (1), (2) трансформируется в систему

∂U f,s      ∂P f,s

∂X

∂X

-

л dU_s

AW

-

dU f dY

∂P f,s ∂Y

^{1    9} 2

+ Re,. dY 2 ⁺ K" f,s

= 0;

01 ^{1 f} dY=2

U f,s (0,Y ) = 1;

U fs (X,0) = f        = 0 ,

где X = x/h;

Y = x/h;

-

U f,s ) ;         (7)

^U f,s = ^u f,s ^{/ u} o ^{; V} f,s = ^u f,s ^{/ u} 0 ^P f,s = ^{p / ( p} f,s ^u o ) ^; A =

α s ρ s ₃ ε

α f ρ f πu ² ₀

µ f

16 p s r

)   ; Re f,s = u _o p f,s h/ f ; K f,s = kh/ (a f,s P f,s U o ).

Пусть dU fs /дХ = 0, тогда dP f,s /дХ = dP fs /dX = C f,s и из (6) - (11) получим:

1 d²U f A dU dU f Re f dY ² — ar — ay

1 d 2 U s Re s dY ²

+ K f (U s ^{- U} f ) ^- C f = ^0;

+ K s (U f ^— U s ) ^— C s = ⁰;

U fs ⁽0) =     /' = 0

с сохранением балансового соотношения фаз (9). В [22] экспериментально обнаружено, что скорость дисперсной фазы в ядре потока неброуновских суспензий опережает дисперсионную, а вблизи стенок плоского канала наоборот из-за миграционного эффекта, что предполагает наличие локализаций равенства скоростей. В связи с этим сопряженная нелинейная система (12) – (14) представлена эквивалентной линейной системой уравнений через аксиальную плоскость отсутствия скольжения фаз, с координатой Y о , которая является, по-существу, параметром модели

1 d^w f    _л Г dW s ⁽¹⁾

Re f dY ^{2 + Р} дҮ

- "W'Y   + K f   ^W 1 - ^w- ]

- 1 = 0;

Rd.. + Ks [Wf1) - pW-1’] - p=0; es i d2w(2)      Г ;мг2    "w(2)1       г

Re f У- ^- у ^- -YrK f И^{2) -} f ^{- 1}=⁰

i^d^ + Ks W2) - pws2)] - p = 0; es dW(2) (1)    |IH''.(2)(1)

W f ¹ ’ (0) = W , ⁽¹ > (0) =     f ; ’ =     ‘_⁽ ) = 0;

dY       dY

w (1 ( Y 0 ) = W f ² ’ ( Y 0 ) , Wl ¹ ’ ( Y 0 ) = W . ⁽² ’ ( Y 0 );

dW f ¹ ’ ( Y 0 ) _ dW f ² ’ (Y 0 ) dW s¹'’ (Y 0 ) _ dW'(' (Y,)

dY = dY ’    dY   = dY ’

где Wi1;2’ = U(Y2) /Cf,s; p = pf/ps; Wi1, WH’ - определены на Y e [0, Y0) и Y e [Y0,1] f s         f s                               f s f s соответственно;

! Y0 [ w 0

-

Ws(1)] dY = / ■

Y 0

W ( ²⁾ - W ( ²⁾ dY. fs

2.    Решение

Выразив из (16) и (18) W _f ^(1,2)

w R2) = 4— + ж(1,2)— d2Ws(1,2)1 f     p (Ks + s     ResKs dY2 ] (23) и подставив полученные выражения соответственно в (15) и (17), получим вместо

(1 2)

системы (15) – (21) следующую систему относительно W s ^, :

d4Ws(1,2)           d3Ws(1,2)                           d2Ws(1,2)                          -1 4  T ARef  3Y3    (ResKs + Ref Kf)  2ү2  =  Ref Res (Kf + p ) . dY          dY                    dY (24) W1) (0) = dWdYRi = 0; W    (Yo) = W ' (Yo) : (25) (26) dWs(1) (Yo) = dWs(2) (Yo) dY = dY ; с дополнительными краевыми условиями (27) d2 Ws(1) (0) dY 2   = R. (28) d3Ws(2) (1) _ dY3      0; d3Ws(1) (Yo) _ d3Ws(2) (Yo) dY3    = dY3   . d2Us(1) (Yo) _ d2Us(2) (Yo) dY2         dY2   ’ при безусловном выполнении (22). Решение системы (24) – (31): (29) (30) (31) Us(1,2) = c!1,2) + c21,2) Y + c31,2) exp (±Г2Y) + c41,2) exp (±r3Y) + (Y2, (32) где r23 = (a ± V a2 + 4b) /2; a = ARef; b = ResKs + Ref Kf;

( = [ Re f Re s ( K f + p ^{- 1} )] / [2 (Re s K s + Re f K f )];

C (1) = d j r ^^ f l ^- / 2 )-(- Г 2 / 1 + Г з / 2 )].

• ^{4      ( f} 1 - ^f 2 ^{) ( r} 3 e 1 - ^r 2 e 2 ⁾ - ^{( e} 1 - ^e 2 ^{) ( -r} 2 f l + ^r 3 ^f 2⁾ ’

C (2) = de 1 ⁽ r 3 - r 2 ⁾ .

• ^{4      ( f} 1 - ^f 2 ^{) ( r} 3 e 1 - ^r 2 e 2 ⁾ - ^{( e} 1 — ^e 2 ^{) ( -r} 2 ^f 1 + ^r 3 ^f 2⁾ ’

e 1 = r 2 exp ( Г 3 Ү 0 ) ,e 2 = r 2 exp ( Г 2 Ү 0 );

f 1 = r 3 exp (— Г 3 ) exp (— Г 2 Y o ) / [ r 2 exp (— Г 2 )] , / 2 = r 2 exp (— Г 3 Y o ); d = (2 ( — Re s ) exp ( Г 2 Ү 0 );

C ⁽¹⁾ — —^/2/r ²C⁽¹⁾ — 2A /r²+ Tie lr ²-C⁽²⁾ — I— г³ехпГ/ It ³ exn Г —ГоШ С⁽²⁾-

C 3 =    r 3/ ¹ 2 C 4      ² ^ / ¹ 2 ⁺ Re s/ ¹ 2 . C 3    = t ^r 3 ^{exp (   r} 3 ⁾ / [^r 2 ^{exp (} r 2 ⁾_| J C 4 .

(1)           (1)        (1)

C 1 = C 3     C 4 ;

C (2) = [exp ( Г 2 Ү 0 ) (1 - Г 2 Y o ) - 1] C (1) + [exp ( г з Y o ) (1 - Г 3 Ү 0 ) - 1] C 41) -

• - [exp (-Г2Yo) (1 + Г2Ү0)] C'(2 - [exp (-Г3Ү0) (1 + Г3Yo)] c42);

3.    Анализ

C? ) = - C 31) Г 2 exp ( r 2 Y o ) - cf ) Г 3 exp ( r 3 Y o ) + [- Г 2 exp (- r 2 Y o ) +

+ Г 2 exp (- Г 2 )] C 32) + [- Г 3 exp (- r 3 Y o ) + Г 3 exp (- Г 3 )] C ⁽²⁾ - 2 ( ;

C22) = r2C32) exp (-Г2) + гзС^ exp (-Г3) - 2(, а из (23) и (32) следует

W f ^1,2) = p / K s - 2 p( /Re s K s + pC (1 ^,2) + pC 2 ^1,2) Y +

+ p [1 - r | / (Re s K s )] C^ ²⁾ exp (± r 2 Y ) +                    (33)

+ p (1 - r 2 /Re s K s ) C ( ^1,2) exp (± r 3 Y ) + p^Y 2 .

Для примера рассмотрена изотермическая броуновская суспензия при температуре 293 ° K , движущаяся в плоском канале высотой h =0,1 м со средней скоростью u 0 =10 ^{- 3} м/с, в которой вода с плотностью p f = 1000 кг/м ³ и динамической вязкостью ^ f =1,00340 - 3 Па^с является дисперсионной средой, а частицы песка плотностью p _s = 2400кг/м ³ , со среднечисленным радиусом r =10 - 5 м и объемной долей a _s = 0,01 образуют дисперсную фазу. Из-за незначительности концентрации частиц их столкновением можно пренебречь и поэтому гидродинамическая обстановка около какой-либо частицы не влияет на другие и тогда справедливо соотношение [23]

^sf ^f (1 as/am)     , которое коррелирует с уравнением Эйнштейна [24] для свободнодисперсных систем при малых αs, где αm= 0,68 – объемная доля частиц в осадке,

/- sf     ^ f ⁽¹ + ² , ^{5 a} s ) .

Коэффициент лобового сопротивления определен формулой Стокса [25]

k = Qnr^ f .

Для нахождения параметра модели Y ₀ был принят следующий алгоритм: задавались Y 0 из Y 0 € [0 , 1; 0 , 9] с шагом 0.1; считая профиль скорости W f ^1,2) ( Y ) реперным, где Y € [0 , 1], определяли нормирующий коэффициент для W _s ^(1,2) ( Y ) из условия сохранения постоянства расхода суспензии через поперечное сечение канала; вычисляли относительную ошибку выполнения условия (30) для каждого Y 0 , аппроксимируя значения точности параболической зависимостью, коэффициенты которой идентифицировали методом наименьших квадратов; после чего по найденной таким образом зависимостям рассчитывали Y ₀ , соответствующий минимуму отклонения.

Вычислительными экспериментами установлено, что зависимость Y ₀ от u ₀ ∈ [10 - 6 ; 10 ^{- 2} ] несущественна, причем Y о ~ 0 , 6. Отметим также, что величина Y о коррелирует с экспериментальными данными из [22, 26] Аналогичный вывод сделан и при изменении r € [10 - 5 ; 10 ^{- 4} ], а также для h € [0 , 01; 0 , 2], что согласуется с выводами в [27] для неброуновских суспензий. Несмотря на то, что дрейф Y 0 отсутствует, уве-

• a) б)

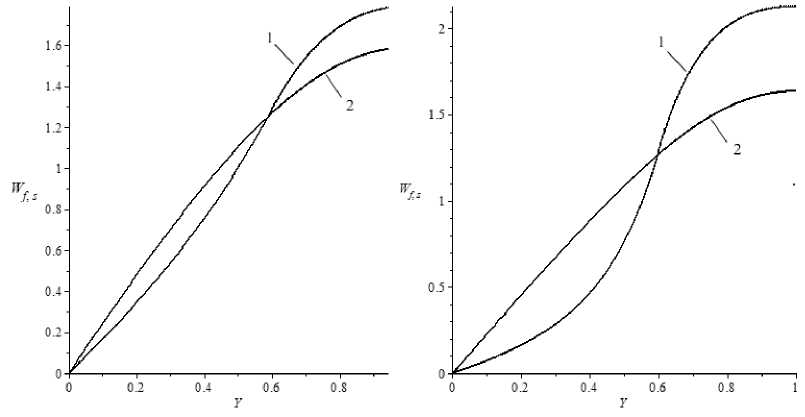
Рис. 1 . Профили скорости дисперсионной W _f (1) и дисперсной W _s фаз (2) суспензии вода-монодисперсные частицы кварца при различных скоростях u ₀ , м/с: а – 10 ^{- 4} ; б – 10 ^{- 3}

• a) б)

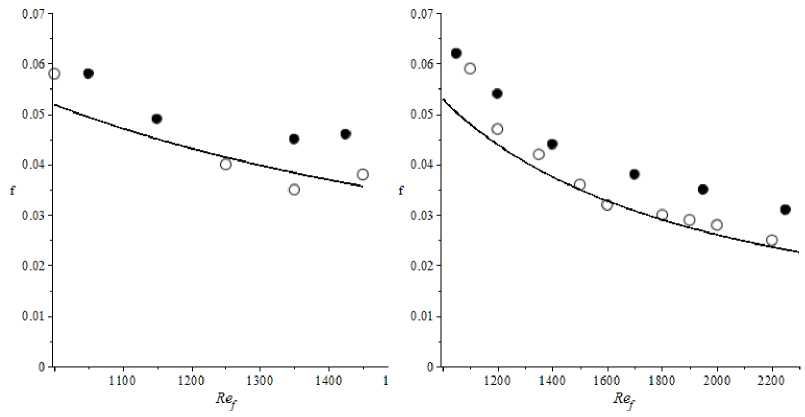
Рис. 2 . Зависимость коэффициента сопротивления от числа Рейнольдса для различных наножидкостей: а - H 2 O/A1 2 O 3 ; б - H 2 O/CuO (о - эксперимент; сплошная линия - расчет; • - H 2 O)

личение скорости потока приводит к большему опережению скорости частиц вблизи стенки и к большему их отставанию в ядре потока (рис. 1), причем максимальная скорость фаз на оси канала больше скорости жидкости без дисперсионной фазы, равной 1,5. Рис. 2 иллюстрирует согласование результатов расчетов с известными экспериментальными данными [20] по коэффициенту сопротивления f = rw/ (0,5pf u0) (тw -касательное напряжение на стенке) при напорном ламинарном течении наножидкостей в горизонтальных каналах, которые подтверждают корректность предложенной модели и предсказывает снижение сопротивления течению броуновских суспензий по сравнению с гомогенной жидкой средой.

Заключение

Учет давления частиц в уравнении для дисперсионной фазы объясняет наличие разных локальных скоростей частиц и жидкости. Линеаризация давления частиц в среднеквадратичном приближении позволила получить точное аналитическое решение уравнений двухжидкостной модели путем введения параметра Y ₀ , являющегося координатой аксиальной плоскости, в которой скорости фаз равны. Расчетный анализ подтвердил правомерность такого подхода и показал существование локального различия профилей скоростей частиц и несущей среды, аналогичное как для неброуновских суспензий.