Напряженно-деформированное состояние статически неопределимых металлических конструкций

Анализ работы строительных конструкций показывает, что аварии возникают в результате случайного совпадения нескольких факторов: отклонения нагрузки в худшую сторону; снижения механических свойств материала; неблагоприятных условий эксплуатации; неточности расчетной схемы и т.д.

Ведущие советские специалисты Н.С. Стрелецкий, А.А. Гвоздев, С.С. Давыдов и др. на основе глубоких обобщений, сделанных в различных областях строительных конструкций, разработали метод расчета строительных конструкций по предельным состояниям. Этот метод в 1955 г. был принят в строительных нормах и правилах, а в 1971-1976 гг. значительно усовершенствован. Принципы расчета по предельным состояниям позже нашли отражение в нормативной документации многих зарубежных стран.

Действующий СНиП предусматривает две группы предельных состояний: 1-я – по потере несущей способности или непригодности к эксплуатации; 2-я – по непригодности к нормальной эксплуатации.

Вероятностно-статистический характер метода расчета по предельным состояниям позволяет определить надежность проектируемых конструкций и объектов, оперируя случайными величинами или научно обоснованно рассчитать вероятность их отказа (вероятность наступления того или иного предельного состояния).

Основными факторами, от учета которых зависит надежность строительных конструкций, являются: нагрузки и воздействия; прочностные, деформационные и другие свойства материалов; условия работы; геометрические размеры сечений; степень ответственности сооружения. Нагрузки, действующие на конструкцию, прочностные характеристики материалов, из которых конструкция изготовлена, обладают изменчивостью и могут отличаться от средних значений. Поэтому для предотвращения наступления любого из предельных состояний вводится система расчетных коэффициентов, учитывающих возможные отклонения (в неблагоприятную) различных факторов, влияющих на надежную работу конструкций.

Расчетные коэффициенты устанавливают на основе вероятностно-статистических методов [2]. Они гарантируют с учетом экономической целесообразности требуемую надежность работы конструкций для всех стадий: изготовления, транспортирования, возведения и эксплуатации.

Таким образом, основная идея метода расчета по предельным состояниям заключается в обеспечении условия, чтобы даже в тех редких случаях, когда на конструкцию действуют максимально возможные нагрузки, прочность материалов минимальна, а условия эксплуатации наиболее неблагоприятны, конструкция не разрушилась и не получила бы недопустимых перемещений или местных перемещений. При этом во многих случаях удается получить более экономичные решения, нежели при расчете ранее применявшимися методами.

Рассмотрим расчет металлической рамы с криволинейнo-наклонным ригелем (рис. 1). При проектировочном расчете данной рамы, нагруженной расчетной нагрузкой, считались заданными геометрические размеры рамы, а также схема нагрузок.

Н

Исходные данные: q_e = 20000    ; l = 3 м.

м

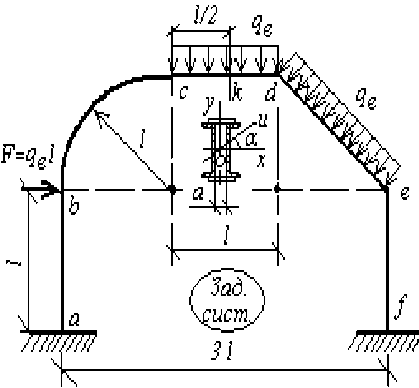
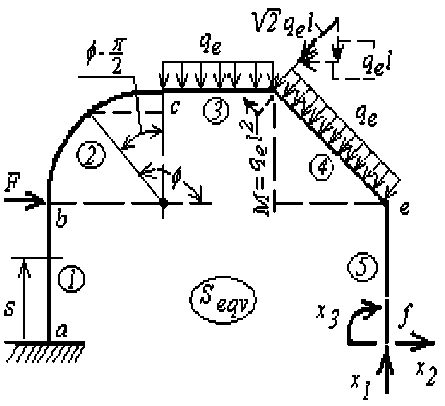
Рис.1. Расчетная схема и эквивалентная система рамы с криволинейно-наклонным ригелем

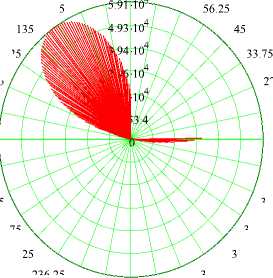
Рама 3 раза статически неопределима внешним образом. Вычисления выполнены в математической программе MathCad [1]. Ниже представлен пример программного модуля для криволинейного участка рамы и результаты в графическом виде (рис. 2).

112.5

123.75

101.25 90 78.75

₄       67.5

146.25

157.5

191.25

202.5

168.75

^Mtot2 ⁽ φ ^{) o} 180

22.5

11.25

348.75

337.5

213.75

326.25

236.25

247.5

258.75 27 φ 0

303.75

292.5

281.25

Рис.2. Графический результат M_tot для криволинейного участка рамы

Mtot2 ^ф =

п

0 if 0 <  ф <-

[■>/ ^п

• — x r 2- l + l * siH ф—~

¹ к к    2,

—

I          I       п

• ■ x l + 1 * cos ф—~

² к       к   2,

.

if ^ <  ф < п

I ^{l п} ||       ,2

+ Хэ + q•l * — + l * sin ф—~   + q * l ...

з e \ 2 к 2)) e

I /1 ^п

+q*i* i +l*s^4 ф— e I к   2,

—

I I п q„ * l * l — l * cos ф—~ e к к 2,

Решая канонические уравнения для эквивалентной системы получаем эпюры суммарных изгибающих моментов M_tot ( s ) , поперечных Qy ( s ) и нормальных N ( s ) сил для заданной рамы (рис. 3).

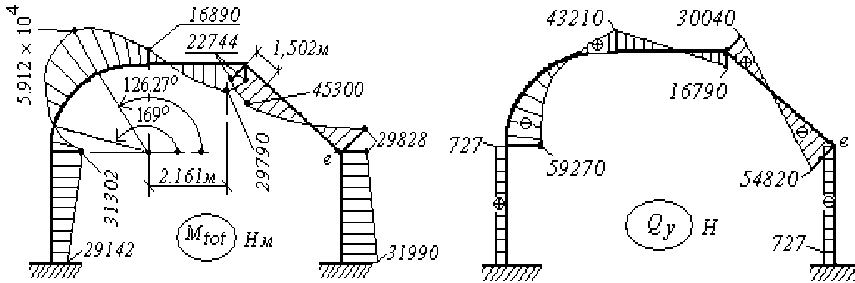
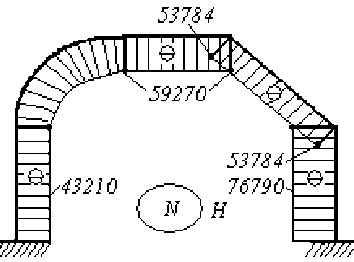
Рис. 3. Суммарные эпюры Mtot,

Q y

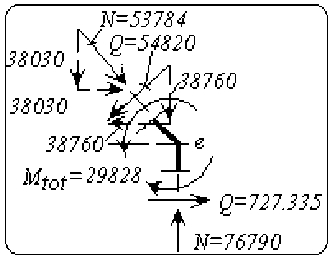
и N для заданной рамы и равновесие вырезанного узла <е>

Для контроля правильности расчета проведены вычисления в программном комплексе AN-SYS [3] (рис.4).

Проверка рамы на жесткость. Максимальный по абсолютному значению прогиб (стрела прогиба), как правило, приурочен к середине пролета рамы. Условие жесткости рамы заключается в том, чтобы стрела прогиба не превышала предельного прогиба, предусмотренного нормами проектирования:

fmax fu

В зависимости от назначения конструкции величину предельного прогиба принимают

f I

^u к 200

—

1 (

* l

,

где l - пролет рамы.

В нашей задаче величина предельного прогиба посередине пролета равна f •=       -3-1

^Ju' 300

fu = ^{3 см}

.

Как видно, вычисленное значение прогиба посередине пролета < be > находится в пределах допустимых значений:

δ 2_k f_u .

Оценка напряженно-деформированного состояния металлической рамы с криволинейнo-наклонным ригелем, нагруженной расчетной нагрузкой, позволила определить оптимальные размеры сечения рамы, которую предложено выполнить из двух швеллеров №18. Разработана методика расчета строительных рам в среде Mathcad и ANSYS.

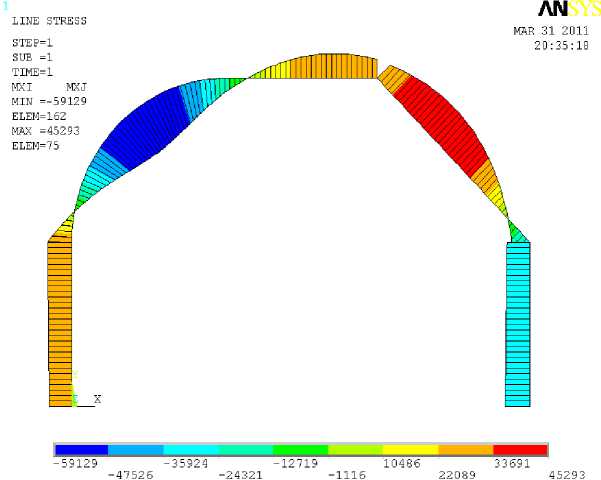
Рис.4. Суммарная эпюра M_tot в программном комплексе ANSYS