Напряженное состояние Г-образных тонкостенных стержневых соединений при изгибе-кручении

Темой тонкостенных стержней и тонкостенных стержневых систем активно занимаются с середины XX века. Важнейшую роль в сфере создания концепции расчета тонкостенных стержней сыграли такие российские ученые, как В.З. Власов, А.А. Уманский, А.Р. Ржаницын, А.Р. Туснин, В.И. Сливкер, K. Saade, А.В. Перельмутер, В.В. Юрченко, B.W Schafer, C. Szymczac, Z.Q. Wang, J.C. Zhao, I. Kreja, R. Pavazza, J.H. Gong, M. Vukasović и другие.

В последние годы (2015-2021гг.) были решены различные задачи статики [1]–[5], динамики [6],[7] и устойчивости [8]–[12] данных конструкций. Однако многие другие задачи и проблемы, в том числе уже рассмотренные, требовали и продолжают нуждаться в более глубоком и детальном изучении.

Одна из таких проблем касается подхода к выражению краевых условий в узлах. Существуют различные гипотезы учеты бимомента в узлах.

Одной из первых предложенных гипотез, предложенной еще во второй половине ХХ века заключается в том, что бимоментом в узловых соединениях пренебрегают [13]: на конце стержня депланация либо полностью отсутствует (абсолютно жесткий узел), либо не встречает никакихпрепятствий (шарнир относительно депланации). В то же время опубликована книга [14], в которой предполагалось также, что пространственная ориентация стержня не влияет на депланацию, т.е. депланация в общей и местной системе координат считается одинаковой. Также Rybakov, V.; Jos, V.

Stress State of Г-Shaped Thin-Walled Rod Joints in Bending Torsion;

в 1982г. Ю.И.Немчиновым [15],[16] была защищена докторская диссертация по методу конечных элементов в механике тонкостенных пространственных и стержневых конструкций.

В работах [17]–[19] рассматриваются различные типы тонкостенных конечных элементов и методики численного расчета для исследования стержневых конструкций, пригодные лишь для частных случаев.

А.Р. Туснин в 2003г. сначала в докторской диссертации, а затем и в последующих трудах [20]–[23] и прочих, при расчете систем тонкостенных стержней методом конечных элементов с помощью построенных им тонкостенных конечных элементов с 7 степенями свободы с помощью точной аппроксимаци предложил гипотезу о том, что мера депланацияя θ ^/ не изменяется при повороте, т.е. равен для всех стержней, сходящихся в одном узле. Результаты данной теории нашли применение в программном комплексе СТК. Данная гипотеза использована им в матрице поворота при принятии косинуса поворота соответствующей степени свободы, равного единице. При этом в статье [21] утверждается, что «…коэффициенты преобразования депланации определяются конструкцией узлов сопряжения стержней, направляющие косинусы зависят от геометрии конструкции», но ответа, как это сделать, автор не дает.

Несколько позже профессор А.В. Перельмутер и В.В. Юрченко проверили данные подходы к учету граничных условий и пришли к выводу, что значения бимомента отличны в сходящихся в узле стержнях и не имеют как таковой зависимости [24],[25].

В дальнейшем профессор А.Р.Туснин в работе [26] в развитие данной темы исследует экспериментально граничные условия для различных типов узловых опорных соединений и выявляет количественные характеристики, позволяющие инженерам-расчетчикам их использовать в расчетных схемах, отличных от стержневых систем с идеализированными опорами – шарнирными или жесткозащемленными. При этом тема внутренних узловых соединений для плоских и пространственных рам не затронута.

В работе Е.И.Бритвина [27] также подтверждается несостоятельность гипотезы непрерывной передачи депланации через узел. В рамках классической теории В.З.Власова предлагается метод расчета пространственных стержневых тонкостенных конструкций, учитывающий неравенство депланаций подходящих к узлу сечений, и построения матрицы жесткости узла с помощью сочетании анализа конечноэлементной модели узла с последующим ее «обжатием» при помощи аналитических построений. Указанная работа, по мнению авторов данной статьи, является важным этапом в развитии теории тонкостенныхт стержней.

В работах профессора Серпика И.Н. и Школяренко И.О. [28],[29] и др. также рассмотрена тема стестенного кручения в Г и Т-образных стержнях, так же, как и в остальных рассмотренныхт работах показан существенный дисбаланс по бимоментам на стыках стержней корытообразного профиля и предложен итерационный процесс определения соответствующих коэффициентов матрицы жесткости тонкостенного стержня путем изменения расположения вспомогательных связующих элементов между стержнями.

Каждая предложенная из гипотез при расчете систем, состоящих из тонкостенных стержней, дает отличный друг от друга результат, что приводит к отсутствию четкого понимания методики расчета подобных конструкций, и в свою очередь может стать причиной разрушения конструкции, которая может быть запроектирована неверно. Данное положение отражает актуальность темы данной статьи.

Для того, чтобы принять наиболее подходящий способ учета бимомента в узлах тонкостенных стержневых систем с целью их дальнейшего расчета и обеспечения необходимой несущей способности, необходимо более подробно изучить явление стесненного кручения в данных узлах.

В соответствии с этим, целью работы является анализ напряженно-деформированного состояния упруго-податливых узловых соединений двух тонкостенных стержней открытого профиля, имеющих различные параметры, находящихся в условиях стесненного кручения ( объект исследования ), и определение соответствующего коэффициента поворота сечения.

Для достижения поставленной цели сформулированы задачи , заключающиеся в создании и расчете в программном комплексе ABAQUS пространственных конечно-элементных моделей узловых соединений, выполненных из тонкостенных стержней:

• 1)    под разными углами;

• 2)    разной жесткости;

• 3)    с учетом конструктивных элементов узлового соединения.

Для каждого замоделированного узлового соединения необходимо исследовать характер передачи бимомента и определить коэффициент поворота.

Основным допущением является идеализация узлового соединения – гипотеза сплошности, однородности и изотропности соединяющихся друг с другом элементов; в работе не рассмотрены дополнительные конструктивные элементы, такие как метизы (за исключением задачи 3), сварка, фрикционная работа элементов и др.

Целью работы НЕ является изучение характера работы конструкции в узле для заданных параметров, т.к. эта тема является более, чем изученной в мировой литературе и научного интереса, с точки зрения строительной механики, по мнению авторов, не представляет. Указанное допущение принято в данной работеисключительно для изучения предмета исследования - явления поворота бимомента как силового фактора, составляющего НДС тонкостенного стержня, в частных задачах о стесненном кручении Г-образной рамы.

Обозначенная проблема уже неоднократно рассматривалась авторами настоящей статьи в [30],[31] и др., где было высказано предположение о том, что значения бимомента В 1 и В 2 в двух стержнях (а следовательно – и бимоментные напряжения σ 1 и σ 2 в их узловых сечениях , сходящихся в узле, имеют зависимость, и их отношение определяется коэффициентом поворота К ω .

B о ~ to ^ Кю

ω

B ₂ σ ₂

B ₁ σ ₁

Данный коэффициент поворота используется в матрице поворота [С] двухузлового стержневого конечного элемента (14х14), которая в случае пространственного элемента будет иметь вид:

[ ^С 1 ^]

0 )

[ C ] ==

к

К _Ш1

^{[ С} 2 1

к

^1V ол 7

где [ С 1 ] и [ С 1 ] матрицы коэффициентов поворота по «стандартным» степеням свободы в первом и втором узле, соответственно; К ω1 и К ω - коэффициенты поворота «седьмой» (депланационной) степени свободы.

В настоящей статье основной акцент сделан на анализ полученных результатов, определение возможных зависимостей и формирование соответствующих выводов. Процесс создания конечно-элементных моделей узловых соединений в программном комплексе ABAQUS, рассматриваемых, в статье не рассматривается.

2    Materials and Methods

К конечно-элементной модели Г-образного соединения (рис.1) вдоль полок сечения со стороны ригеля приложена линейная распределенная «единичная» нагрузка с максимальным значением 1кН, моделирующая действие бимомента (рис.2). Нижние грани «колонны» представленного узлового соединения жестко закреплены от перемещений и поворотов.

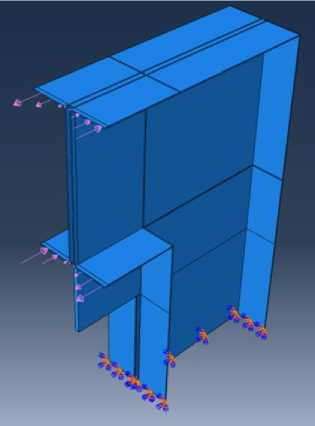
Рис. 1 – Модель узлового соединения в ПК ABAQUS

Fig. 1 – Joint model in PC ABAQUS

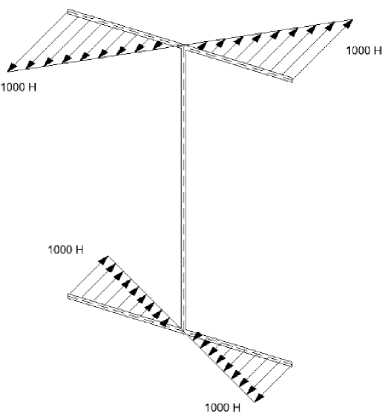
Рис. 2 – Единичная нагрузка

Fig. 2 – Unit load

Характиристики узлового соединения представлены в табл. 1.

Таблица 1. Геометрические и физические параметры узлового соединения

Table 1. Geometric and physical parameters of the rod joint

Характеристика		Значение	Ед. изм.
Плотность	р	7858	кг/м3
Модуль Юнга	Е	2∙1011	Па
Коэффициент Пуассона	V	0,3
Размеры тонкостенного профиля		0,2х0,05х0,0015	м
Длина «ригеля»		0,105	м
Длина «колонны»		0,45	м
Размеры фасонки		0,3х0,3х0,006	м

В программном комплексе ABAQUS было замоделировано узловое соединение. Модель узлового соединения разбита на 8-ми узловые конечные элементы первого порядка интерполяции и с редуцированной схемой интегрирования (C3D8R) размером 5х5х1,5 мм (рис. 3-4).

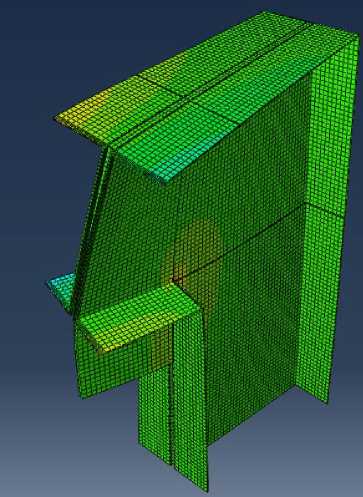
Рис. 4 – Деформированное состояние узла

Fig. 4 - Strain state of joint

Рис. 3 – Конечноэлементная модель

• Fig. 3 – Finite element model

Далее методом конечных элементов вычисляются нормальные напряжения в четырех наиболее опасных точках наиболее близких к узлу (расположенных на расстоянии одного конечного элемента) сечений ригеля и колонны σ1A1 , σ1B1 , σ1C1 , σ1D1,σA22 , σB22 , σC22 , σD22 (рис. 5-6)

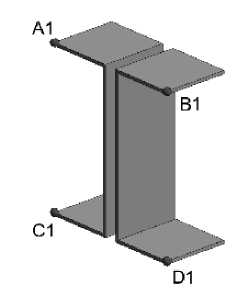
Рис.5 – Расчетные точки в «ригеле» Fig. 5 – Reference poins in «beam»

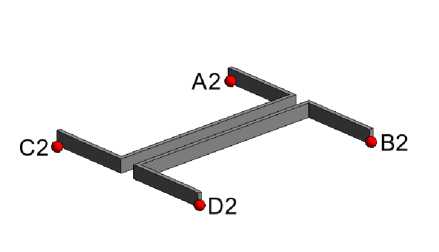
Рис.6 – Расчетные точки в «колонне»

Fig. 6 - Reference poins in «column»

Напряжения в пределах полки усредняется по модулю для обеих полок (формула (3)), вычисляются отношения средних величин (формула (4), которые затем еще раз усредняются и, таким образом, получается «коэффициент поворота» K ω .

σ1t =1/2 (σ1A1+σ1B1) ; σ1b =1/2(σ1C1+σ1D1)

σt2   B2 ; σb2   B2

σ1t    B1 σ1b

3 Results

• 3.1    Узловые соединения тонкостенных стержней, сопряженные по разными углами

Рассмотрим 4 случая, при которых профили, образующие узловое соединение, сходятся под углами 105˚, 120˚, 135˚, 165˚ (рис. 7-14). Приложем к ригелю каждой из моделей ранее описанную «единичную» нагрузку. Основани вертикальной части жестко закрепим.

Узловое соединение из тонкостенных профилей, сопряженных под углом 105˚, его геометрические параметры, схема приложения нагрузки и закрепления показаны на рис. 7-8.

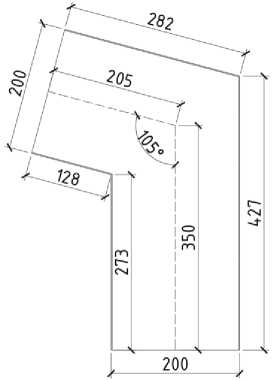
Рис. 7– Размеры узлового соединения под углом 105˚

Fig. 7 – Joint dimensions at the angle of 105˚

Аналогичная информация по соединению углом 120˚, показана на рис. 9-10.

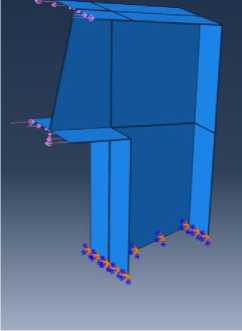
Рис. 8 – Модель узлового соединения под углом 105˚

Fig. 8 – Joint model at the angle of 105˚

из тонкостенных профилей, сопряженных под

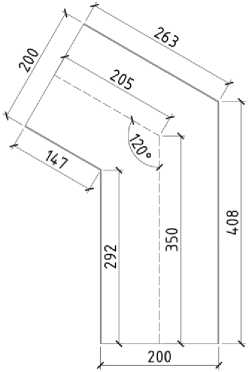
Рис. 9 – Размеры узлового соединения под углом 120˚

Fig. 9 – Joint dimensions at the angle of 120˚

Аналогичная информация по соединению

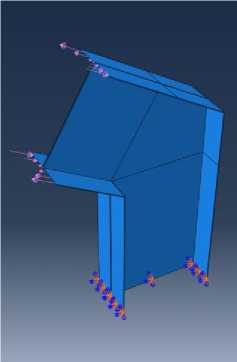
Рис. 10 – Модель узлового соединения под углом 120˚

Fig. 10 – Joint model at the angle of 120˚

из тонкостенных профилей, сопряженных под

углом 135˚, показана на рис. 11-12.

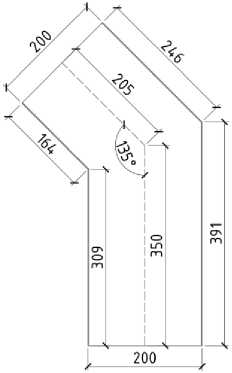
Рис. 11 – Размеры узлового соединения под углом 135˚

Fig. 11 – Joint dimensions at the angle of 135˚

Аналогичная информация по соединению углом 165˚, показана на рис. 13-14.

Рис. 12 – Модель узлового соединения под углом 135˚

Fig. 12 – Joint model at the angle of 135˚

из тонкостенных профилей, сопряженных под

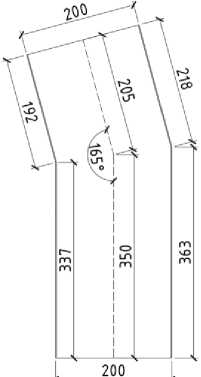
Рис. 13 – Размеры узлового соединения под углом 165˚

Fig. 13 – Joint dimensions at the angle of 165˚

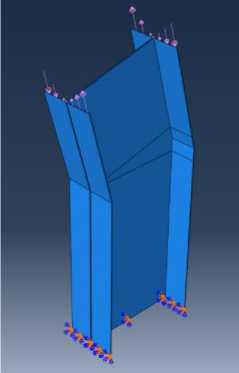
Рис. 14 – Модель узлового соединения под углом 165˚

Fig. 14 – Joint model at the angle of 165˚

Результаты расчета сведены в табл. 2 в виде значений нормальных напряжений в соответствующих точках (рис.5-6) и вычисленного коэффициента поворота.

Таблица 2. Результаты вычисления коэффициента поворота для узловых соединений из тонкостенных профилей под разными углами Table 2. The results of calculating the rotation coefficient for the joint models made of thin-walled profiles connected at different angles

Нормальные напряжения в «ригеле», кПа

Нормальные напряжения в «колонне», кПа

2 σ t = B 2 σ 1 t     B 1

2 σ b 1 σ b

= B 2 B 1

Kto

1 σ A1

1 σ B1

1 σ C1

1 σ D1

1 σ t

1 σ b

2 σ A2

2 σ B2

2 σ C2

2 σ D2

2 σ t

2 σ b

о

X о. ф CD

X о. 0) CD

со т

со т

■qT X ® CD Ф

■qT 0) со т S ц Т ф о.

X о. 0) CD

X о. CD CD

co T

co T

X ® Ф g CD Ф

'ф Ф co т S d T 0) Q.

X Q. Ф CD 3< Q. Ф CD

co "ro T

Ф Ф T CI Ф Q. О

о О)

О со о_ со' СМ

о со о со' см 1

со со о со' см 1

со со о_ со' см

о СО о_ со' см +1

со СО о_ со' см 1+

со 1О 1

со со'

co co CN 'd-

co co CN 'di

co LO' 1+

co co CN 'd" +1

о CM o'

co LO o' 1

О 00 o' 1

LO о

'd" О) О) см

'd" О) О) см 1

со о о_ со' см 1

со о о со' см

'd" О) О) см +1

СО о о со' см 1+

00 00 о о'

co co o_ o' 1

LO О 'd; o' I

LO О 'do'

co co o_ o' +1

LO о 'd; o' 1+

co о о о'

'd- о o'

О О О о'

о СМ

СМ О) СМ

см О) см 1

'd" о_ со' см 1

00 о со' см

см О) см +1

со о_ со' см 1+

00 о о_ со'

CD о co' 1

co CM co' I

CO CN co'

CM o_ co' +1

LO CD CN co' 1+

co о о'

CD o'

CM о'

со со

О) 00 О) см

О) 00 О) см 1

О) 00 О) см 1

О) 00 О) см

О) 00 О) см +1

О) 00 О) см 1+

см со'

CM co' 1

'd- cd' i

'd" 'd; cd'

CM cd' +1

CM 'd; cd' 1+

CM CM CN o'

о CM CN o'

CD CM CN o'

со со

со о_ со' см

со о со' см 1

см о о со' см 1

см о о_ со' см

со о со' см +1

см о о со' см 1+

00 со «0 со'

co co CD co' 1

о co' 1

о co'

co co CD co' +i

о co' s

LO CD CD o'

co CD CD o'

CD CD o'

Вычисленные коэффициенты поворота обобщены на рис. 15 в виде графика зависимости величины коэффициента поворота от величины угла между профилями, образующими узел.

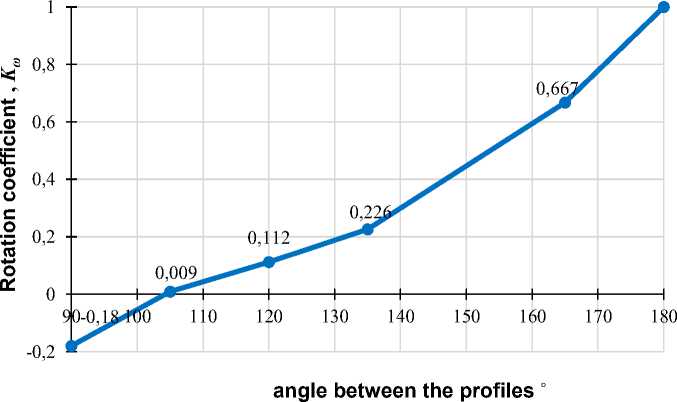
Рис. 15 – Зависимость коэффициента поворота от угла между профилями

Fig. 15 – Dependence of the rotation coefficient on the angle between the profiles

• 3.2    Узловые соединения тонкостенных стержней разной жесткости

В данном разделе был изучен ряд Г-образных пространственных конечно-элементных моделей узловых соединений, выполненных из тонкостенных профилей разной жесткости.

Рассмотрено два основных варианта:

• 1)    при неизменной жесткости профиля «колонны» изменяется жесткость «ригеля» узлового соединения (табл.3);

• 2)    при неизменной жесткости профиля «ригеля» изменяется жесткость «колонны» узлового соединения (табл.4).

Далее приведены сводные таблицы (табл. 3-4) для каждого варианта, где представлены изображения моделей в программном комплексе ABAQUS со схемой приложения нагрузки и закреплениями, наименование используемых профилей для «ригеля» и «колонны», а также полученные значения коэффициента поворота.

Таблица 3. Коэффициенты поворота для моделей узловых соединений, выполненных из тонкостенных профилей разной жесткости (различная жесткость сечения «ригеля»)

Table 3. Rotation coefficients for the joint models made of thin-walled profiles with different stiffness (different stiffness of the beam)

(D К Л S С X X X С 0) -0- 0) m О X О с «	ПН-100-50 1,5	ПН-150-50 1,5	ПН-200-50-1,5	ПН-250-50-1,5	ПН-300-50-1,5
х X ^ х s 5 ф -8- о m ° О с §	ПН-200-50 1,5	ПН-200-50 1,5	ПН-200-50-1,5	ПН-200-50-1,5	ПН-200-50-1,5
К т	-0,113	-0,156	-0,180	-0,195	-0,200

Таблица 4. Коэффициенты поворота для моделей узловых соединений, выполненных из тонкостенных профилей разной жесткости (различная жесткость сечения «колонны») Table 4. Rotation coefficients for the joint models made of thin-walled profiles with different stiffness (different stiffness of the column)

0) К а х х X S С 0) -Q- 0) m X О с «	ПН-200-50-1,5	ПН-200-50-1,5	ПН-200-50-1,5	ПН-200-50-1,5	ПН-200-50-1,5
§ ^ 5 X S 5 ф -8- о m ° О с §	ПН-100-50-1,5	ПН-150-50-1,5	ПН-200-50-1,5	ПН-250-50-1,5	ПН-300-50-1,5
К т	-0,155	-0,168	-0,180	-0,186	-0,194

Изменение жесткости профиля происходит за счет изменения высоты сечения профиля при неизменной ширине и толщине стенок. Диапазон изменения высоты сечения профиля находится в пределах между 100 мм и 300 мм с шагом 50 мм.

На рис. 16 показана зависимость величины коэффициента поворота от высоты сечения «ригеля». При увеличении высоты сечения «ригеля» (от 100 мм до 300 мм) величина коэффициента поворота уменьшается (от -0,113 до -0,200).

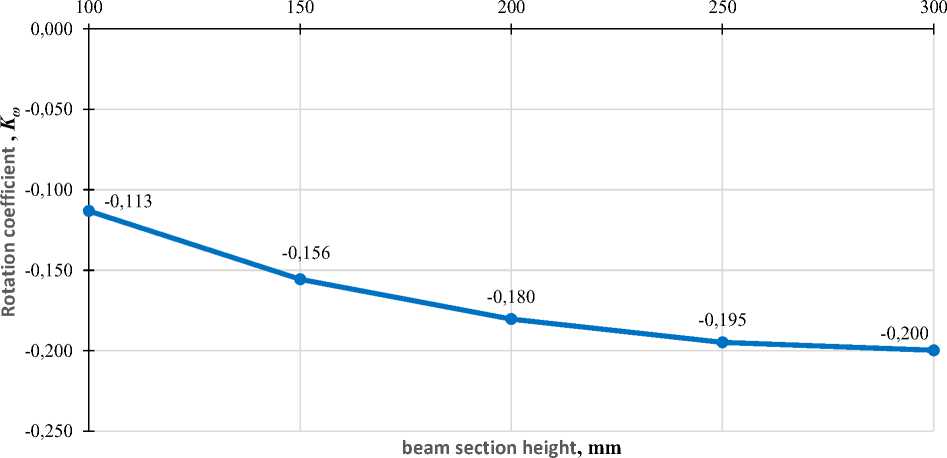
Рис. 16 – Зависимость коэффициента поворота от высоты сечения «ригеля»

Fig. 16 – The dependence of the rotation coefficient on the beam cross-section height

На рис.17 представлена зависимость величины коэффициента поворота от высоты сечения «колонны». При увеличении высоты сечения «колонны» (от 100 мм до 300 мм) величина коэффициента поворота уменьшается (от -0,155 до -0,194).

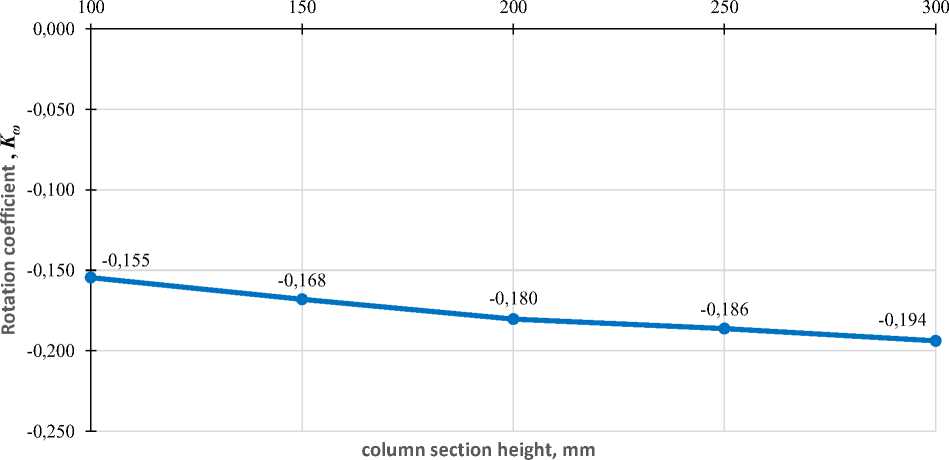
Рис. 17 – Зависимость коэффициента поворота от высоты сечения «колонны»

Fig. 17 – The dependence of the rotation coefficient on the column cross-section height

• 3.3    Учет конструктивных элементов узлового соединения тонкостенных стержней

Рассмотрим вариант болтового соединения двух тонкостенных стержней, которое могло быть запроектировано к рассматриваемой данной статье расчетной схеме.

Основные геометрические размеры соединения представлены на рис. 18-19. Модель данного узлового соединения эквивалентна модели на рис. 3-4, за исключением наличия уголков и болтового соединения из 18 болтов. Отверстия в тонкостенных профилях, фасонке и уголках расположены симметрично относительно линии стыка профилей в узле. Заданы болты М8х16 в стенках профилей и М8х14 в полках (ГОСТ 7805-70 Болты с шестигранной головкой класса точности А. Конструкция и размеры).

Уголки приняты сварными, без радиуса закругления, 75х75х6 в количестве 4шт.. Ширина уголков равна ширине полки тонкостенного профиля – 50 мм.

Отличием от ранее описанных расчетных моделей является особенность назначения связей между составными частями узлового соединения. С целью имитации болтового соединения элементы модели соединены жестко между собой только в местах контакта: 1) поверхности болта с внутренними поверхностями отверстий под него в тонкостенных профилях и фасонке/уголке; 2) внутренней поверхности шляпки болта/гайки с соответствующей поверхностью на тонкостенном профиле/уголке. Допущением рассматриваемой модели является отсутствие учета трения между составными частями узлового соединения.

Рис. 18 – Размеры узлового соединения

Fig. 18 – Joint dimensions

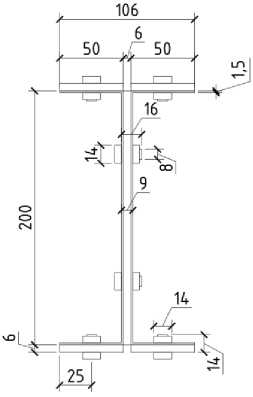
Рис. 19 – Размеры узлового соединения (сечение)

Fig. 19 – Joint dimensions (cross-section)

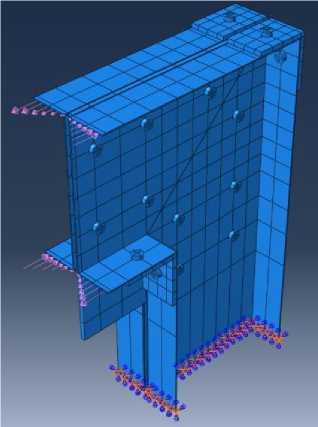
Рис. 20 – Модель узлового соединения с учетом конструктивных элементов Fig. 20 – Joint model with structural parts

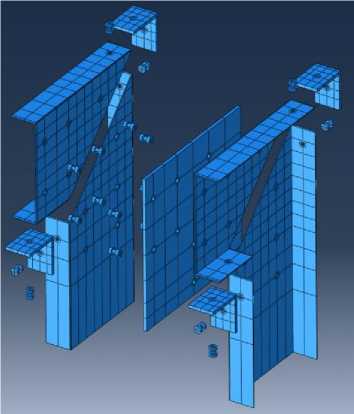
Рис. 21 – Составные части узлового соединения

Fig. 21 – Joint model components

Результаты расчета представлены в табл.5 в виде значений нормальных напряжений в соответствующих точках (рис. 5-6) и вычисленного коэффициента поворота. Также с целью сравнительного анализа в табл.5 приведены результаты расчета аналогичных моделей узловых соединений без фасонки и с учетом фасонки.

Разница в значениях коэффициента поворота при учете конструктивных элементов (фасонки, уголков, болтовых соединений) и без их учета составляет 28,3%. Разница в значениях коэффициента поворота при учете конструктивных элементов (фасонки, уголков, болтовых соединений) и при учете только фасонки составляет 26,7%.

Таблица 5. Результаты вычисления коэффициента поворота для узловых соединений: без учета фасонки, с учетом фасонки, с учетом фасонки и болтового соединения

Table 5. The results of calculating the rotation coefficient for the joint models made of thin-walled profiles: without gusset, with gusset, with gusset and bolted connection

Нормальные напряжения в «ригеле», кПа

Нормальные напряжения в «колонне», кПа

2 σ t = B 2

2 σ b

= B 2

K ro

1 σ A1

1 σ B1

1 σ C1

1 σ D1

1 σ t

1 σ b

2 σ A2

2 σ B2

2 σ C2

2 σ D2

2 σ t

2 σ b

σ 1t     B 1

1 σ b

B 1

ф т С S к 1— Ф х о о

X о. ф аз

X Q. Ф CD

co T

CO T

X ® CD Ф

■qT ф CO T S CI x 03

X Ф CD

X Q. Ф CD

co T

CO T

'ф x ® CD Ф

'ф Ф го т s d x аз

X Ф CD 3< Ф CD

co "ro T

Ф Ф T Ф Q. О

со 5 0) о -8-

о LO О га' Cd

о LO o_ to' Cd 1

от LO от' Cd i

co LO о to' Cd

О LO o_ to' Cd +i

CO LO o_ to' Cd 1+

CO LO' 1

to LO'

to to CN 'd-

to to CN 'di

to LO' 1+

to to CN 'd-+i

О Cd o'

co LO o' 1

О to o' 1

о О о го -8-

'd- CD см

'd; cd' Cd 1

'd; cd' cd i

'd- cd' cd

'd- cd' cd +i

'd- cd' cd 1+

03 CM 'd" 1

03 CN 'd"

°3_ 'd-

°3_ 'di

03 CN 'd-1+

°3_ 'd-+i

'd" CD o'

co o' i

CD o' 1

°  5 s х Si X J3 03 О 03 х 5 О S о S 5 го н а * 5§ О ю о

от 'd" cd' Cd

Cd Cd 'd; cd' Cd

CM 'd; cd' Cd

03 о 'd- cd' cd

о co 'd- cd' cd +i

to 'd- cd' cd 1+

CD 'd" 03 cm

'd" CD 03 Cd'

'd-co to co'

03 to co'

LO LO Cd' 1+

LO °° co' +1

Cd o' 1

CD 'd o' i

03 Cd o'

При этом стоит учитывать тот факт, что в рассмотренной модели не назначались дополнительные связи трения между составными элементами узлового соединения. Можно предположить, что при учете трения, значения нормальных напряжений и коэффициента поворота будут ближе к значениям, полученным для моделей без учета конструктивных элементов.

На основании вышеизложенного, представляется возможным сделать вывод, что более детальная проработка конечно-элементной модели узлового соединения, при учете таких конструктивных элементов, как фасонка, уголки и болтовые соединения, оказывает незначительное влияние на получаемые значения нормальных напряжений в расчетных точках, и соответственно, на значение коэффициента поворота.

Учитывая результаты проведенных расчетов всех рассмотренных узловых соединений и выявленные зависимости значения коэффициента поворота от различных изменяемых параметров, в узловых соединениях, выполненных из тонкостенных профилей, сопряженных при угле равном 90˚, имеет смысл рекомендовать принимать значение коэффициента поворота, расположенное в диапазоне -0,1 <  К _ш < -0,2 в зависимости от наиболее невыгодной ситуации.

4 Discussion

При анализе результатов следует отметить отличие всех полученных в данной статье результатов от результатов, которые можно получить по теориям и методикам других авторов, занимавшихся исследованием узловых соединений тонкостенных стержней.

В целом, подтверждены для Г-образных соединений результаты, ранее опубликованные в трудах А.В.Перельмутера и В.В. Юрченко [25],[24] для Т-образных и др. узлов. В очередной раз подтвержден факт того, что ни бимиомент как силовой фактор, ни депланация как вид деформации не остаются постоянными по разные стороны от узлового соединения, как это позиционируют некоторые авторы.

Однако особое внимание следует обратить на результаты численного эксперимента по вариации угла между элементами

Видно, что при увеличении угла между профилями, образующими узловое соединение, увеличивается значение коэффициента поворота. Причем при определенном угле коэффициент поворота меняет свой знак с отрицательного на положительный. Этот угол приблизительно равен 105°, в этом случае коэффициент поворота равен K _w = 0,009 .

В результате проведенных расчетов определены области применения ранее известных гипотез: А.Р. Туснина [20] и А.С. Городецкого и др.[13] .

Как уже отмечалось ранее, гипотеза А.Р. Туснина [20] заключается в том, что косинус угла поворота бимомента принимается равным единице, что в свою очередь, согласно рис. 15, соответствует углу 180˚ между профилями, образующими узловое соединение.

В гипотезе А.С. Городецкого и др. [13] бимоментом в узлах пренебрегают, что говорит о равенстве нулю косинуса поворота бимомента. Данная ситуация, согласно рис. 15, справедлива для узлового соединения, образованного сопряжением профилей при угле 105˚. Соответственно, при угле равном 105˚ передача бимомента через узловое соединение отсутствует.

5 Conclusions

• 1.    Выявлена зависимость величины коэффициента поворота от высоты сечения одного из профилей, образующих Г-образное узловое соединение. Показано, что при увеличении высоты сечения (т.е. жесткости) одного из профилей, образующих Г-образное узловое соединение, уменьшается величина коэффициента поворота.

• 2.    Выявлена зависимость коэффициента поворота от угла между профилями, образующими узловое соединение. Показано, что при увеличении угла между профилями, образующими узловое соединение, увеличивается значение коэффициента поворота.

• 3.    Показано существование такого угла между профилями, образующими узловое соединение, при котором коэффициент поворота равен нулю, а именно - меняет свой знак с отрицательного на положительный. Для рассмотренной задачи такой равен около 105˚, в этом случае коэффициент поворота равен K ω =0,009, что говорит о том, что бимомент в узле не передается. Можно считать, что данная конфигурация узлового соединения является частным случаем, соответствующим гипотезе [13], авторы которой считали, что бимоментом в узлах пренебрегают.

• 4.    Учет таких конструктивных элементов, как фасонка, уголки и болтовые соединения, оказывает незначительное влияние на характер передачи бимомента в узловом соединении, и как следствие, на значение величины коэффициента поворота.

• 5.    В узловых соединениях, образованных тонкостенными профилями, сопряженными при угле 90˚, рекомендовано принимать значение коэффициента поворота, находящееся в диапазоне - 0,1 ≤ K ≤ - 0,2 в зависимости от наиболее невыгодной ситуации расчета.