Напряженное состояние металлических защитных покрытий в критических условиях нагружения

Непрерывная тенденция к увеличению энергии импульса газодинамических импульсных устройств (ГИУ) приводит к необходимости защиты канала трубы от высокоскоростного потока топливных продуктов горения (ПГ), действующих при высоких температурах и давлении. За один цикл, время которого составляет несколько сотых долей секунды, защитное покрытие и материал поверхности трубы испытывают переменное напряженно-деформированное состояние (НДС), так, что его компоненты меняют свое направление от положительных величин до отрицательных и наоборот [1,3].

В работах (1 – 4) проведено исследование условий функционирования гальванического хромового защитного покрытия трубы ГИУ. Нанесение таких покрытий приводит к образованию слоя, толщиной от 100 до 300 мкм, обладающего высокой твердостью и адгезионной стойкостью, однако, как показывает металлографический анализ (Рисунок 1), структура покрытия обладает не-сплошностями, характеризуемыми множеством мелких трещин.

EDN ISZDNQ

а)                                                 б)

Рисунок 1 - Структура гальванического хромового покрытия : а) - микроструктура (увеличение 400; б) - сетка трещин (увеличение 100; вид с поверхности)

Микротрещины будут образовываться в покрытии из-за остаточных напряжений во время нанесения и последующей термической обработки (обезводороживании). Трещины выходят на поверхность покрытия, образуя сетку повреждений. При нагружении трубы давлением и температурном воздействии на нее со стороны ПГ в покрытии появляются напряжения, значение ко- торых могут приводить к выходу трещин на поверхность и к появлению дополнительной сетки трещин.

Опыт эксплуатации ГИУ показывает, что в подобных критических условиях нагружения происходит развитие повреждений (трещин) покрытия, через которые ПГ проникают к основе, способствуя ее эрозионному разрушению и, в конечном итоге, покрытие сходит, оголяя защищаемую поверхность основы (Рисунок 2).

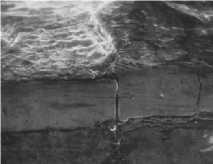
Рисунок 2 - Последовательность повреждаемости защитного хромового покрытия при функционировании ГИУ

Процесс повреждения защитного покрытия в трубе ГИУ можно приблизительно разделить на две фазы: растрескивание и удаление фрагментов с поверхности.

Процесс растрескивания определяется структурой и сплошностью материала покрытия, которые обеспечиваются в процессе гальванического процесса. В результате появляются отдельные фрагменты, которые могут разделяться на более мелкие в зависимости от значений компонентов НДС по отношению к определяющим критические условия.

Процесс схода хромового покрытия происходит в соответствии с конфигурацией, образованной сеткой трещин, путем постепенного удаления отдельных изолированных фрагментов хрома из-за разрушения металла на границе раздела хром-сталь или вблизи нее.

Материал покрытия - хром, который обладает более высокой теплопроводностью по сравнению со сталью (Табл. 1). При этом увеличение его толщины не приводит к значительному

Г.В. Лепеш, М.В. Басова увеличению тепловой защиты, однако приводит к изменению НДС. Компоненты НДС в значительной мере определяют механизм разрушения покрытия и его защитную стойкость от схода при эрозионном воздействии потока ПГ.

Точность результатов анализа НДС также в значительной степени зависит от точности определения механических характеристик материала теплозащитного покрытия, свойства которого оказываются зависимы от технологических параметров гальванического процесса. Наиболее значим модуль упругости Е, оказывающий влияние на значение напряжений и предел прочности ств, определяющий критические условия разрушения покрытия. Измерение его величины в покрытии представляет определенные трудности, а приведенные различными авторами значения (Табл.1) значительно разнятся. Причем их величина может превышать модуль упругости стальной основы, иметь значение меньшее его или быть равным, что оказывает существенное значение на результаты при определении НДС в покрытии.

Модуль упругости определяли экспериментально на образцах, аналогичных, применяемых в работе [3] путем многократных измерений, распределенных по толщине покрытия и зоне адгезии. Для испытаний применялся сканирующий зондовый микроскоп комплексного исследования НаноСкан-3D (Рисунок 3). Значение модуля упругости получали путем непосредственной обработки результатов измерений (Рисунок 4). Адекватность измерительного процесса производилась путем сопоставления полученных результатов с результатами измерения модуля упругости стальной основы, значение которого известно и составляет Е =210 ГПа.

Таблица 1 – Физические характеристики хромового гальванического покрытия

№ пп	Наименование, обозначение, размерность	Значение
		Покрытие	Труба
1.	Температура плавления, Т пл , К	2129	>1300
2.	Удельная теплоемкость, с , кДж/кг	0,46	0,48
3.	Плотность, р, кг/м3	7190	7850
4.	Коэффициент теплопроводности, Л , Вт/(м К)	93,7	48
5.	Коэффициент термического расширения, а , К-1	6,2х10-6	11,5х10-6
6.	Модуль упругости, Е , ГПа	240[4]; 250 [5], 170 – 210 [6]	210
7.	Коэффициент Пуассона	0,12	0,29
8.	Предел прочности при растяжении, <г в , МПА	700	1500

Рисунок 3 – Сканирующий зондовый микроскоп комплексного исследования НаноСкан-3D

В результате получено Е_Х р =201 ± 6 ГПа. Математическое ожидание полученного значения в дальнейшем применено в расчетах по определению НДС.

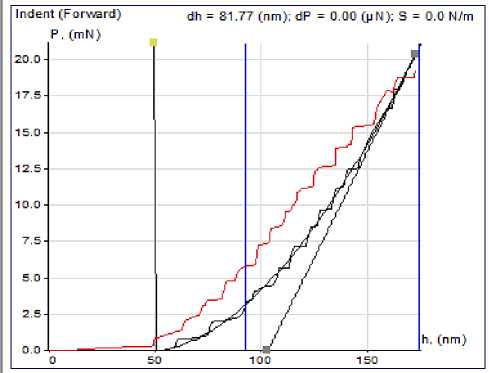
Рисунок 4 – Результат определения модуля упругости (вид с интерфейса)

Для моделирования геометрии дефрагментированного покрытия использовался графический редактор ANSYS – SpaceClaim. Участок трубы с поверхностным дефектом, имеющим небольшую кривизну, представлен в виде плоского элемента толщиной, кратно превышающей толщину покрытия, что исключает влияние на результаты расчета граничных условий закрепления модели.

Сложный процесс нагружения элемента защитного покрытия учтен последовательным нагружением усилиями растяжения, сжатия и сдвига, имитирующими тангенциальные и сдвиговые напряжения при функционировании ГИУ.

На рисунке 5 приведены примеры картин НДС фрагмента поверхности канала трубы растягивающими, сжимающими и сдвиговыми деформациями, соответственно, имитирующими нагрузку, испытываемую материалом трубы, расположенным вблизи ее поверхности, в реальных условиях функционирования ГИУ.

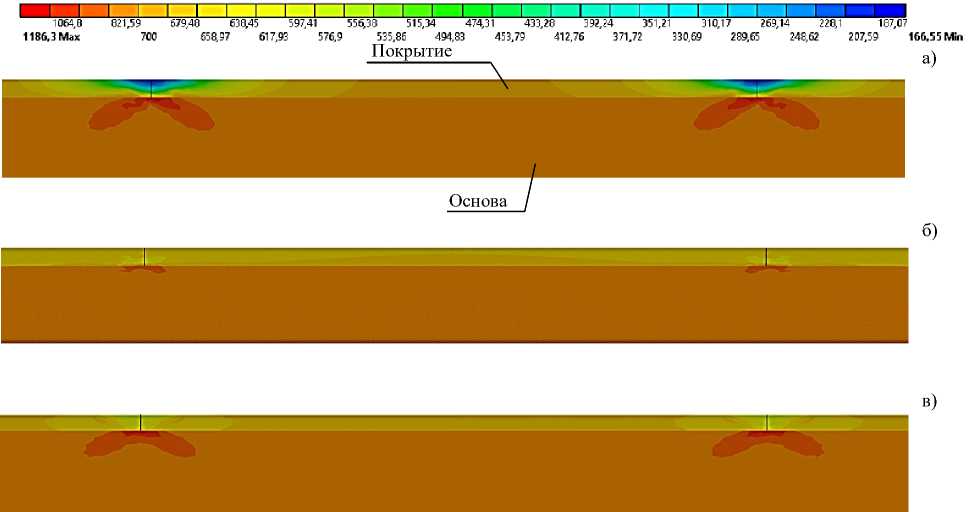
Рисунок 5 – Напряженное состояние поверхности трубы ГИУ : а) – при растяжении; б) – при сжатии; в) – при сдвиге

Результаты (Рисунок 5) показывают, что наибольшие напряжения в покрытии достигаются в середине фрагмента покрытия, а также непосредственно вблизи трещины в металле основы в виде концентраторов напряжений.

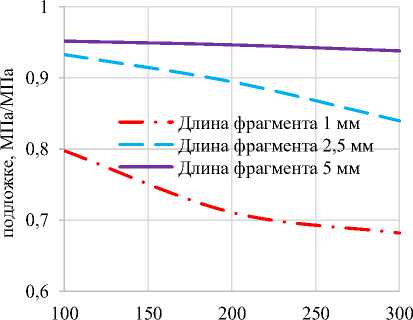
В случае растяжения разрушающие напряжения в середине фрагмента покрытия достигаются при значениях тангенциальных напряжений в поверхности несколько больших, чем напряжения в покрытии (Рисунок 6 и 7). В то время как граница фрагмента разгружена. При достижении напряжениями критических разрушающих значений фрагмент покрытия ровно по середине (при равномерной сплошности) разделится на два блока, для дальнейшей фрагментации которых потребуется несколько большее усилие. При чем, как следует из построенных графиков (Рисунок 6 и 7), критические условия наступают раньше при уменьшении толщины покрытия и увеличении размеров образующихся фрагментов (длины).

Толщина покрытия, мкм

Рисунок 6 – Зависимость напряжений в покрытии от его толщины при растяжении

При сжатии (Рисунок 8 и 9), как и в случае растяжения, напряжения в подложке превышают критические разрушения хромового покрытия при значениях напряжений в основе больших критических. При этом падение разрушающего напряжения с увеличением толщины наблюдается только у мелких по длине фрагментов, длина которых не превышает 2-х мм.

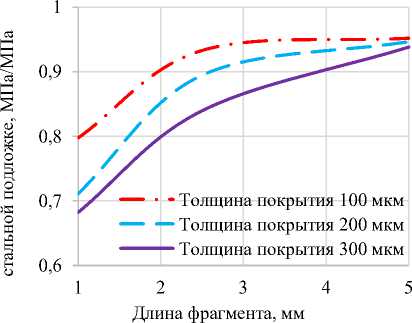
Рисунок 7 – Зависимость напряжений в покрытии от длины фрагментов при растяжении

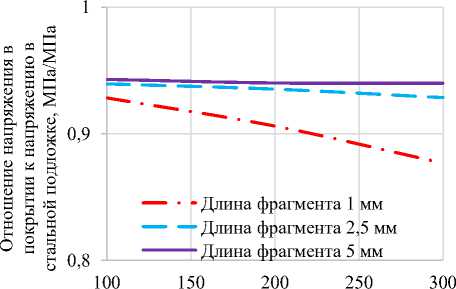
Толщина покрытия, мкм

Рисунок 8 – Зависимость напряжений в покрытии от его толщины при сжатии

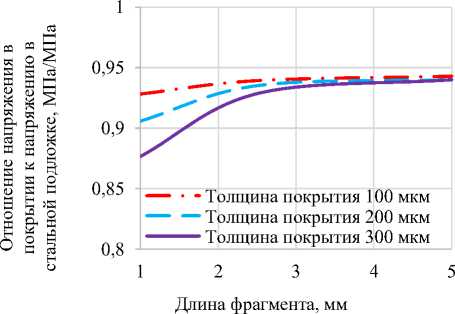
Рисунок 9 – Зависимость напряжений в покрытии от длины фрагментов при сжатии

В случае сдвига распределение НДС по толщине покрытия и основы подобное растяжению (Рисунок 10 и 11), однако числовые значения разнятся.

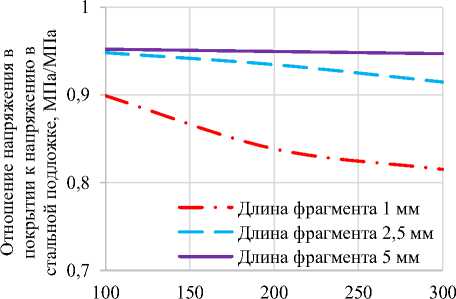
Толщина покрытия, мкм

Рисунок 10 – Зависимость напряжений в покрытии от его толщины при сдвиге

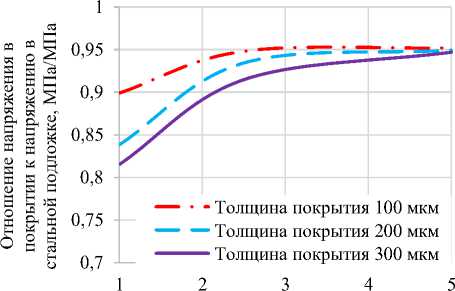
Длина блока, мм

Рисунок 11 – Зависимость напряжений в покрытии от длины фрагментов при сдвиге

Вне зависимости от схемы нагружения, расчетные значения критических напряжений достигают наибольших значений при значениях интенсивности напряжений в основе

E

Ot>—Oxp, (1)

где E и E_X p - модули линейной упругости основы и хромового защитного покрытия соответственно;

о_х р - предел прочности хромового покрытия (400 – 700 МПа [6]).

Достижение условия (1) соответствует образованию новых трещин.

Так как основной причиной, вызывающей НДС поверхности канала трубы, является нагружение ее давлением и тепловым потоком ПГ, то размеры образующейся разгарной сетки, определяющей размеры фрагментов покрытия, будут зависеть от их интенсивностей. Для примера нагружения трубы ГИУ переменной тепловой и силовой нагрузкой, изменяющейся в процессе импульса от значений растягивающих напряжений 01 = 0,85охр до сжимающих о3 = -0,7охр [3], на основании зависимости (1) и построенных графиков (Рисунок 7) получим соотношения между толщинами хромового покрытия и размерами фрагментов (Таблица 2).

Таблица 2 – Размеры фрагментов защитных покрытий

Толщина покрытия, мкм	Длина фрагмента при растяжении, мм
100	1,8
200	2,4
300	3,6

Анализ влияния сжимающих напряжений (Рисунок 9) величиной 0 3 = —0,7о хр показывает, что фрагменты образовываться не будут. Следовательно, сжимающие напряжения такой величины не приведут к дополнительной сетке разгара защитного покрытия, а напряжениями, определяющими разгарную сетку трещин, являются растягивающие напряжения.

Следует отметить, что размеры фрагметов покрытий будут уменьшаться с увеличением интенсивности термосилового воздействия на защищаемую поверхность трубы ГИУ.

Представленные на рисунке 5 результаты НДС следует рассматривать в качестве исходных данных для оценки усталостной прочности в соответствии моделью циклического разрушения поверхности раздела покрытий.

Рассмотрим картину НДС при растяжении более подробно (Рисунок 12).

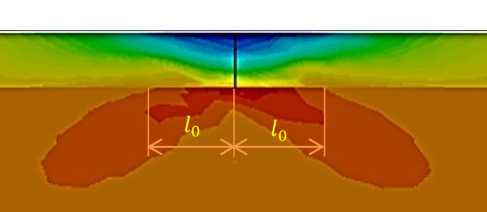
Рисунок 12 – Концентрация напряжений в области трещины в покрытии

Здесь видно, что у вершины трещины образуется концентрация напряжений, величина которых в металле основы будет определять его циклическую прочность в соответствии с классической теорией усталости. В процессе проектирования трубы ГИУ рассчитывают на циклическую прочность по условию наличия у них внутренних дефектов в значительной мере превышающих размеры трещины. При этом нет необходимости рассматривать процесс развития трещины вглубь металла стенки трубы.

На границе раздела фаз между покрытием и основой значения напряжений вблизи трещины превышают критические охр. Несмотря на то, что разрушения здесь не происходит, с точки зрения циклической прочности, можно рассматривать эту зону, ограниченную условием о > охр в качестве условной трещины, размером l0 для целей прогнозирования ее роста при циклическом нагружении.

Поскольку в случае ГИУ трещина на границе раздела является смесью трещин I и II типов, рост трещины на границе раздела будет происходить в зависимости от того, превышает ли коэффициент интенсивности напряжений трещины I или II типа соответствующую вязкость разрушения на границе раздела.

Так в работе [6] для коэффициентов интенсивности напряжений трещин I или II типа получены следующие выражения:

К! = —0,561 • о/йЦ; (2)

К_п = 0,367 • о/йГ₀. (3) Откуда следует, что отрицательное К₁ свидетельствует о невозможности роста трещины в I -режиме (в режиме отрыва). Значение К_п, хотя ияв-ляется положительным, но имеет относительно низкое значение из-за отсутствия открытой трещины, что также делает маловероятным рост трещин второго типа. Следовательно, рост трещин на границе раздела вряд ли может произойти при отсутствии открытой трещины.

Условия развития условной трещины могут появиться при наличии угла θ между направлением действующих напряжений (напр., σ ) и плоскостью трещины в соответствии с уравнениями [8]:

К ;

оу = —== cos

*   /2пГ о

-(1 —sin-sin у-)+ •••; (4)

ог = —, 11 sin—(1 + cos —scos —) +—. (5)

*    72^10   2        2     2

Такие условия могут появиться в двух случаях:

во-первых, при появлении осевой нагрузки приложенной к поверхности канала трубы, например, вызванной силами трения или газодинамическим воздействием потока ПГ;

во-вторых, на конической части канала трубы.

Первый случай характерен при наличии открытой трещины, вызванной наличием дефек- тов покрытия, что способствует их развитию и последовательному полному сходу фрагментов (Рисунок 13). Второй случай характеризует появление первоначального схода покрытия с перехода конической в цилиндрическую часть трубы, где при наличии ненулевого значения угла θ, совокупность факторов, оказывающих влияние на стойкость теплозащитного покрытия может достигать критических значений.

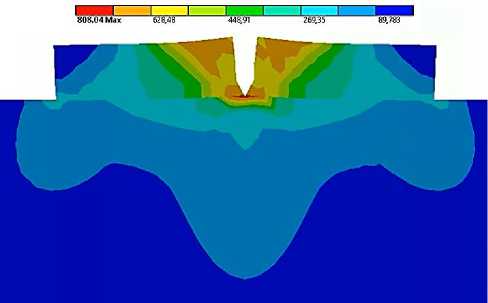
Рисунок 13 – Раскрытие трещины под давлением ПГ (масштаб деформаций 20:1)

В результате проведенных испытаний [3] было установлено, что адгезионная прочность хромового гальванического покрытия превышает прочность на разрыв как хрома, так и стальной основы. Поэтому можно утверждать, что разрушение поверхности раздела покрытия с основой при циклическом нагружении будет определяться вязкостью разрушения стали вблизи границы раздела. При этом критерием роста трещины на границе раздела фаз будет являться условие:

К ! >  K_Ic, (6) где K_Ic - трещиностойкость стали.

Для прогнозирования стойкости теплозащитных покрытий с учетом полученных закономерностей, составляющих основу механизма их разрушения необходимо помимо основных факторов, оказывающих влияние на НДС, учитывать факторы внешнего нагружения, приводящие к появлению сил, способствующих раскрытию трещин.

В результате численных исследований модели теплозащитного гальванического хромового покрытия трубы ГИУ разработан механизм его разрушения при термосиловом нагружении в условиях функционирования. По результатам моделирования НДС трубы ГИУ установлена зависимость между компонентами НДС и размерами фрагментов покрытия, образующимися в процессе нагружения трубы ГИУ термосиловым воздействием со стороны потока ПГ.

В результате проведенного анализа стойкости покрытия при циклическом нагружении установлено, что прогнозирование процесса схода хромового теплозащитного покрытия возможно при включении в расчетную модель дополнительных факторов, учитывающих краевые эффекты при наличии раскрытой трещины и давления газодинамического потока на ее поверхность.