Напряженное состояние пародонта в области пластинчатого имплантата при окклюзионной нагрузке

В настоящей работе исследуется напряженное состояние пародонта в области пластинчатого имплантата при действии окклюзионной нагрузки. Сравниваются напряжения, возникающие при использовании имплантата с гладкой поверхностью и имплантата с пористыми вставками из титана [1]. Пористые вставки обеспечивают надежное сцепление с костной тканью и, как следствие этого, создают условия более равномерного распределения напряжений в губчатой кости.

Состояние проблемы

Жевательный аппарат и его исправная работа являются важными условиями здоровой жизни человека. В процессе жизнедеятельности по причине болезни или по иным причинам человек со временем теряет часть своих зубов. Эти потери не

восстанавливаются природой, и жевательный аппарат утрачивает свои функциональные способности. В медицине разработаны способы компенсации утрат, например, одним из них является внедрение имплантата в кость. К факторам, определяющим успешность применения имплантата, относятся его форма, применяемый материал, место расположения в кости. Конструкция зубного имплантата должна обеспечивать оптимальные условия для передачи давления на костные структуры тела челюсти.

С применением методов порошковой металлургии появилась возможность создания микрорельефной поверхности эндооссальной части имплантата различной степени шероховатости с заданным размером пор. Строение пор также можно варьировать. В зависимости от применяемого метода закрытые, или тупиковые, поры получаются с использованием методов массопереноса частиц в вакууме (электроннолучевое, плазменное напыление); открытые сквозные поры – с помощью методов спекания [3, 5, 6]. Наличие пор в эндооссальной части имплантата способствует глубинному прорастанию костной ткани в металлическую структуру, в результате чего возникает биологическая фиксация имплантата [1, 2, 4, 7].

Разработки структуры поверхности имплантата в основном касаются цилиндрических видов, хотя пластинчатый имплантат остается методом выбора. Разработанная нами конструкция пластинчатого имплантата позволяет, не изменяя прочностных характеристик и габаритов, увеличить площадь соприкосновения имплантата с костной тканью (А. С. № 19748).

В настоящей работе мы провели исследование напряженного состояния пародонта в области пластинчатых имплантатов с гладкой поверхностью и пористыми вставками при действии окклюзионной нагрузки.

Постановка и метод решения задачи о напряженно-деформированном состоянии пародонта и пластинчатого имплантата при окклюзионной нагрузке

Рассматриваемая задача относится к контактным задачам механики. Имплантат с гладкой поверхностью не имеет сцепления с костной тканью за счет сращивания, и его фиксация обеспечивается конфигурацией и сквозными макроскопическими отверстиями, в которые проникает растущая костная ткань. При окклюзионной нагрузке на контактах имплантата с костью неизбежно образование микрозазоров и уменьшение поверхности контакта, что приводит к локализации напряжений по его фактической поверхности и неравномерной передаче усилий на костные ткани пародонта.

Применение имплантата с пористыми вставками обеспечивает его сцепление с пористой костью по всем боковым поверхностям пористых вставок за счет глубинного прорастания костной ткани в имплантат. Биомеханическая фиксация отсутствует только по гладкой поверхности титанового каркаса пористых вставок.

При постановке задачи принимаются следующие допущения:

• ■    взаимодействие гладкой поверхности имплантата с костной тканью моделируется идеальной односторонней связью;

• ■    контакт пористых вставок моделируется сцеплением;

• ■    расчетная область принята в форме поперечного сечения тела челюсти и имплантата с допущением о плоско-деформированном состоянии;

• ■    окклюзионная нагрузка равномерно распределяется по длине имплантата.

Дифференциальная постановка задачи включает систему уравнений линейной теории упругости с граничными условиями

^ij, j + fi = 0, °ij = Cijkl8kl, 8ij = 2(ui,j + uj,i)’ ui = 0 на Ги ,                                       C1)

P i = oj^ на Г,, , i , j = 1,3 .

дополненные контактными граничными условиями в зонах взаимодействия гладкой поверхности имплантата с костной тканью

^ т = ⁰,

^ ⁺ ^ = ⁰ ^ ° n <  ⁰ ,                     ⁽²⁾

u , ¹ + и^ <  0 ^ o_n = 0 на Г c .

где и П¹ ) — проекция вектора перемещения на внешнюю единичную нормаль к контактной поверхности Г с для области i ( i =1,2), < т_п - проекция вектора напряжения на контактной поверхности на внешнюю единичную нормаль, <7_т - касательная составляющая вектора напряжения на контакте.

Задача (1), (2) эквивалентна задаче минимизации функционала:

и е U : J ( и ) <  J ( v ) V v е U ,

J ( v ) = 1 j ~( v ) .. D .. ~( v ) d Q- j f . vd Q- j P . vdr ,                (3)

• ² Q                  Q         r _a

U = { и е ( C ( Q ) ) ³ : и = 0 на Г_u , u^ + и П ²⁾< 0 на Г с }.

Ограничения на нормальные компоненты перемещений на поверхности контакта выполним с помощью метода внешнего штрафа. Задача (3) в этом случае формулируется как задача минимизации функционала ~             ^v v

• ² Q                   Q          Г _а          ^{2 8} Г_с

на множестве U * = {г/ е ( C ( Q ) ) ³ : и = 0 на Г_и }, ф ⁺ = ( ф + | ф |)/2.

С целью регуляризации решения преобразуем в (4) поверхностный интеграл в объемный:

у- j(I v,',11 ■ '^ 1+ )2dГс =1 jE(v)8,2(v)dQc,(5)

• ^{2 8} Г с

где

v ⁽¹⁾ - v ⁽²⁾ dv„         A h Г sign ( 8 ) + -

8n = П хкП =    , En =--\      , dQ c = A hdTc .(6)

A h     dn 8 L 2

Задача минимизации функционала (4) с учетом замены (5) представляет физически нелинейную задачу теории упругости. Модуль упругости в области Q _с зависит от искомой функции в соответствии с формулами (6). Область Q _с является фиктивной и предназначена для регуляризации решения. Ей приписывается малая толщина A h по направлению нормали к поверхности контакта. Предлагаемый подход позволяет применять к решению задачи метод конечных элементов, при этом контакт двух деформируемых тел моделируется с помощью специальных элементов, имеющих анизотропные свойства.

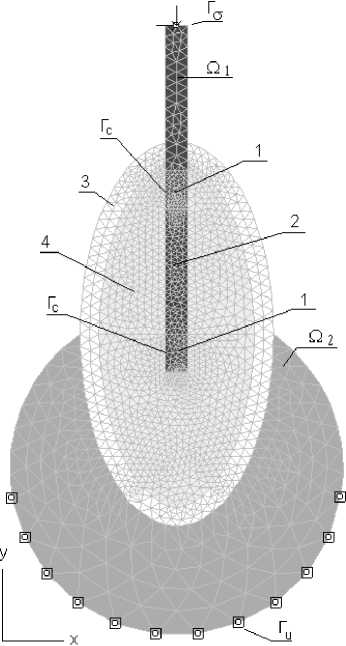
Рис. 1. Расчетная схема: 1 – титановый каркас имплантата, 2 – пористая вставка, 3 – компактная кость, 4 – губчатая кость, Ω 1 –внекостная часть имплантата, Ω 2 –область, моделирующая кинематические граничные условия

Таблица

Материалы и ткани	Модуль упругости, кг/мм2	Коэффициент Пуассона
Альвеола	2000	0,3
Губчатая кость	500	0,3
Каркас имплантата	11000	0,35
Пористая вставка	5476	0,35
Область Ω 2	10	0,3

Анализ контактного давления на костную ткань в области пластинчатого имплантата

Расчетная схема задачи с указанием граничных условий приведена на рис.1.

Область Ω ₁ передает жевательную нагрузку на внутрикостную часть имплантата. Взаимодействие между этой областью и компактной костью отсутствует.

С помощью области Q 2 снимаются концентраторы напряжений в компактной кости и излишняя по отношению к ней жесткость от кинематических граничных условий. При численном моделировании приняты упругие свойства тканей и материала имплантата, приведенные в таблице. Сечение тела челюсти принято в форме эллипса с полуосями 5 и 10 мм. Высота внутрикостной части имплантата 10,5 мм, толщина имплантата 1,2 мм, высота внекостной части 7,5 мм. Имплантат нагружен силами F x = F y =- 0,5 кгс/мм, приходящимися на единицу его длины.

Контактные граничные условия моделировались специальными конечными элементами толщиной 0,025 мм. Эти элементы расположены на расчетной схеме в области контакта каркаса титана с губчатой костью. По поверхности вставок задавалось сцепление с костной тканью. Аналогичные расчеты выполнены для имплантата с гладкими боковыми поверхностями. В этом случае к контактной поверхности относится вся поверхность имплантата.

Результаты расчета представлены на рис. 2, 3.

На рис. 3 масштабированными отрезками показаны направления действия главных напряжений. Выполненные расчеты показывают существенную неравномерность распределения контактного давления и наличие значительного концентратора напряжений в области шейки имплантата. Максимальное давление на костную ткань приходится на верхнюю часть внутрикостной части имплантата. При использовании пористых вставок усилие на костную ткань передается по двум поверхностям. В этом случае максимальный концентратор в области шейки в рассмотренном примере уменьшается на 22%.

Контактное давление в общем случае будет зависеть от индивидуальных особенностей строения тела челюсти (формы, размеров), механических свойств костной ткани и геометрических параметров имплантата, однако, как показывают расчеты, изменение эпюры контактных сил не существенно. В качестве примера на рис. 4 приводится расчет сжимающих напряжений для трапециевидной формы сечения тела челюсти.

Характерными особенностями рассмотренных примеров является линейный закон контактного давления в области наибольшего концентратора. Контакт в этой области составляет примерно 1 мм и не зависит от наличия или отсутствия пористых вставок. Контактное давление на противоположной стороне имплантата и сама область контакта на ней незначительно зависят от типа имплантата и формы челюсти.

Указанные особенности позволяют применить к расчету простые статически определимые модели с учетом предварительно найденных областей контактов и форм эпюр контактного давления.

Статически определимая модель контактного давления в области пластинчатого имплантата

Для быстрой оценки нагрузок на костную ткань, окружающую имплантат, в зависимости от величины и направления окклюзионной силы, а также от геометрических размеров имплантата, в настоящем разделе предлагается статически определимая модель сил, которая строится при следующих предположениях: ■ давление на костную ткань по длине имплантата постоянно, что позволяет рассматривать силы в поперечном сечении;

• ■ распределение давления по высоте имплантата апроксимируется кусочнолинейными функциями;

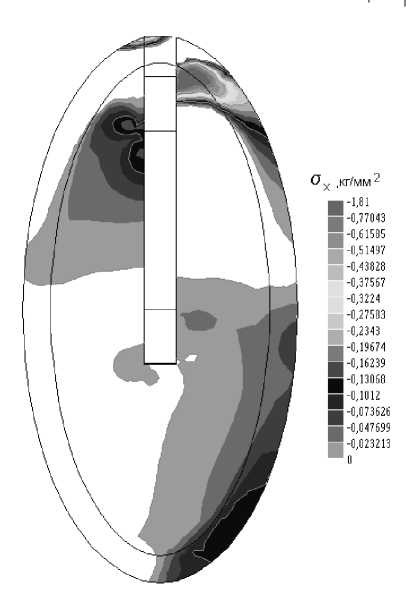
Рис. 2. Области действия сжимающей компоненты напряжений σ x для имплантата с пористыми вставками

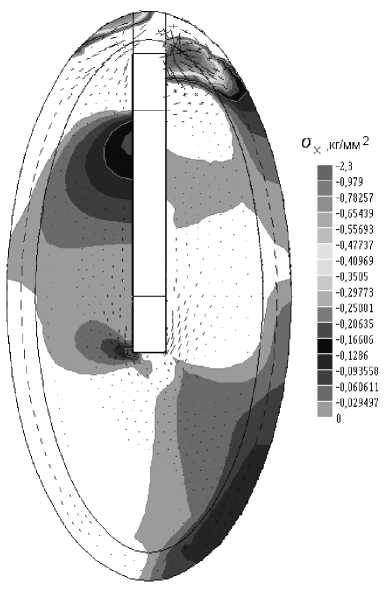
Рис. 3. Области действия сжимающей компоненты напряжений σ _x для имплантата с гладкими поверхностями

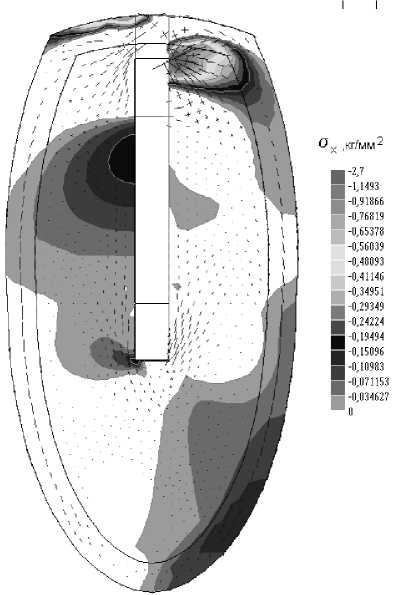
Рис. 4. Области действия сжимающей компоненты напряжений σ x для имплантата с гладкими поверхностями

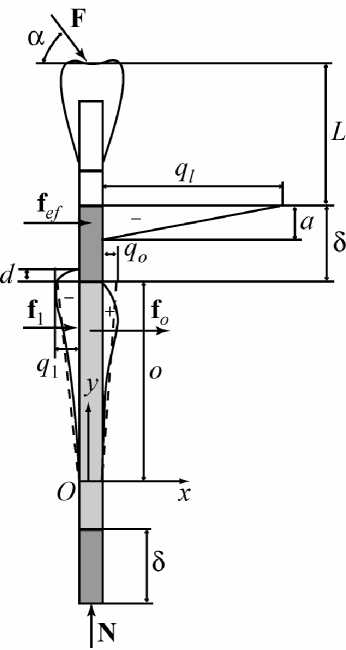
Рис. 5. Расчетная схема имплантата

• ■    поверхности контакта между имплантатом и костью известны;

• ■    реакции кости на противоположных сторонах пористых вставок равны по величине (на одной стороне это напряжения сжатия, на противоположной – напряжения отрыва).

Принятые предположения позволяют построить модель реакций костной ткани. Расчетная схема сил для имплантата с пористыми вставками приведена на рис. 5. При аппроксимации реакций кости линейными функциями (на вставках графики показаны пунктиром) неизвестными величинами принимаются максимальные значения контактных давлений: q ₁ , q ₂ . Для имплантата с пористыми вставками величина q_o находится с помощью последнего предположения. Для гладкой поверхности q o — 0. Знак минус на графиках соответствует сжатию, плюс – растяжению.

Значения параметров a, d , c в общем случае зависят от индивидуального строения кости и, возможно, геометрических параметров пластинчатого имплантата. Этот вопрос требует дополнительных исследований. Однако в простейшем случае для выбранного типа имплантата эти параметры можно в первом приближении считать постоянными.

Считая окклюзионную силу F заданной, составим статические уравнения равновесия для определения неизвестных сил q1 , q2 :

Е F kx ^— f i - f 2 - f o + F cos ^{a —} 0;

k

Е F ky — - F sin a + N - 0;

k

Е M o ⁽ F k ) ^{— —} F ^{cos a (}L ^{+ 8 +} c ) ^— T cf o k 3

^— 3⁽ c + d ) f 1 + (3 a + ^{8 —} a + c ) f 2 - ^0;

q o      q 1

---—-------.

c c + d

Решение этих уравнений относительно неизвестных величин имеет вид:

F f L + a ) x (    3 J q 1 —        —л-----7—. .—?,

c f 5 c 8 a । , cd 8 a ] 11I + (c + d )l1I c + d ( 6   2 6 J \ 6 3 2 6)

Г                      r2     1

² F x ^{+ ( c + d} ) q 1 ⁺ c + d q 1

q 2 ^— -

a

— , F x — F cos( a ).

Для имплантата без вставок главный вектор fo равен нулю. В этом случае решение уравнений равновесия принимает вид:

q i ^-

F x

z f c d 8 a (c + d )l — — — + — — —

( 6   3   2   6

, q 2 ^-

[ 2 F x + ( c + d ) q i ]

a

Величина окклюзионной силы, приходящейся на поперечное сечение имплантата единичной толщины, зависит от числа зубов, замещаемых протезом, величины его окклюзионной поверхности и длины имплантата.

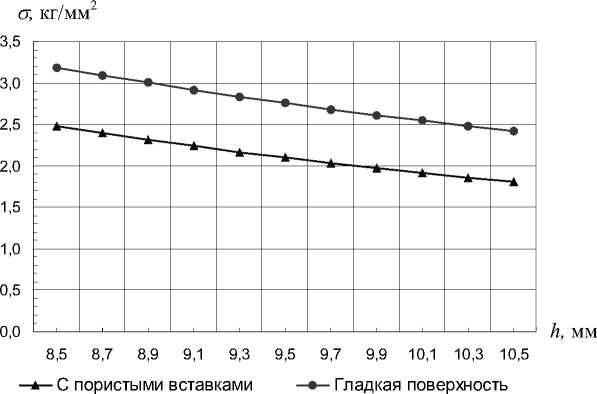
Рис. 6. Максимальное контактное давление на кость

Найдем оценку максимальной силы, приходящейся на имплантат. В предельном случае протез нагружен по всей окклюзионной поверхности. Максимальную силу на один зуб при полном восстановлении окклюзионной поверхности обозначим P . Будем полагать, что фактически действующая жевательная сила пропорциональна площади восстанавливаемой поверхности утраченных зубов и при полном (100% площади) восстановлении будет равна P . Из уравнения статики получается следующая формула для удельной нагрузки на имплантат:

F = —| 1 + 100I

n - 1 ^ P

2 ) 1 ’

где А - восстанавливаемая поверхность утраченных зубов и опорного зуба в процентах от площади оклюзионной поверхности в норме; n - число утраченных зубов, замещаемых протезом; 1 - длина имплантата.

Сопоставление численных результатов с результатами расчетов по формулам (7)-(10) позволило в первом приближении найти значения параметров a, d, c в соотношениях (7)-(9) для тела челюсти с эллиптическим сечением. Для имплантатов со вставками эти значения соответственно равны: a = 0,11 h, c = 0,7(h-5), d = 0,3 мм; для имплантатов без вставок a = 0,11 h, c = 0,8h, d = 0, h - высота внутрикостной части имплантата.

На рис. 6 приведено сравнение по максимальному контактному давлению на кость для двух имплантатов: с пористыми вставками и без применения вставок. Нагрузка и геометрия имплантатов соответствуют приведенным выше условиям решенных численных задач.

Выводы

В работе выполнено исследование контактной нагрузки на костную ткань в области пластинчатого титанового имплантата и аналогичного имплантата с пористыми титановыми вставками. Расчетными методами установлено, что применение вставок снижает максимальное контактное давление на костную ткань на 22%.

На основе численных решений контактной задачи предложена статически определимая модель для расчета контактного давления на кость. Особенности анатомического строения тела челюсти и параметров имплантата учитываются коэффициентами уравнений. Для частных случаев величины этих коэффициентов найдены из решения контактной задачи теории упругости имплантата с телом челюсти. Представляется возможным применение предложенного подхода к построению достаточно простой модели, отражающей основные закономерности напряженного состояния на контакте между имплантатом и костной тканью.