Напряженное состояние упругого толстостенного кольца при произвольно распределенных самоуравновешивающихся давлениях на его внутренней и внешней границах

DOI:

Обобщение задачи Ляме для толстостенного кольца на случай произвольного распределения давлений на его внутренней и внешней границах представляет определенный методический интерес, так как при решении указанной задачи у студентов закрепляются навыки решения краевых задач для областей, имеющих круговые границы с помощью рядов аналитических функций.

Отсутствие решения этой задачи как в научной, так и в учебной литературе объясняется довольно громоздкими преобразованиями, которые необходимо выполнить для получения распределений компонент напряжений.

Общие формулы Колосова-Мусхелишвили

Для упругого изотропного кольца формулы в декартовых координатах имеют вид [1; 2]:

°xx + ° yy = 2И z ) + ^lz) 1

°yy - °xx + 2i°xy = 2 • [z^"(z) + Иz)J, 2 M^(ux + iUy )= к • ф( z)-z^'( z) - ^(z), где °xx, °yy, °xy — компоненты напряжений; ux, uy - проекции вектора перемещений в декартовой системе

E координат; i - комплексная единица; ф(z), ^(z) — функции, голоморфные в кольце (рис. 1); ц = —7---?; E -

2 ( 1 + v )

модуль упругости; v - коэффициент Пуассона; к - константа, определяемая видом напряженного состояния:

3 - 4 v - при плоской деформации;

к = 1 3-v

И + v

–при плоском напряженном состоянии.

Учитывая, что в [1]:

° rr +°ее=° xx + ° yy,

°00 -° rr + 2 i ° re =(° yy -° xx + 2 i ° xy )• e2 i6, где °rr, °66, °r6 - компоненты напряжений в полярной системе координат, вычитаем из первого уравнения системы (4) и, используя (1) и (2), получаем:

° rr ^- i ° r 0 =Ф'⁽ z ^{) +} ^'I z ) ^- z Ф" ( z ^{) -} z •ф'⁽ z ) z

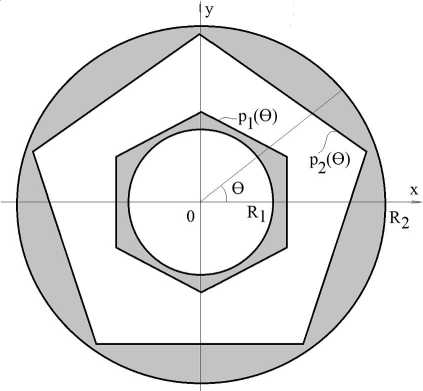
Рис. 1. Кольцо под действием самоуравновешивающегося внутреннего p 1 ( 0 ) и внешнего p 2 ( 0 ) давлений ( R ₁ – внутренний радиус кольца; R ₂ – внешний радиус кольца)

Общий вид комплексных потенциалов, решающих первую основную краевую задачу для кольца в общем случае

Очевидно, что общий вид комплексных потенциалов, решающих задачу для кольца, является простой суперпозицией комплексных потенциалов для линейно упругих изотропных отверстий в плоскости и диска:

где

ф ⁽ z ) =

w ( ^z ) =

⁽ V x ,1 + ^Vx,2 ) + i ^{( V}y ,1 + ^Vy,2 ' 2 n • ( 1 + к )

X

• ln ⁽ z ⁾⁺ E a ik k = 1

_K ^V ,1 ⁺ V x ,2 ^{) -} i ⁽ V y ,1 ⁺ V y ,2 ) 2 п • ( 1 + к )

V x ,1

” Л

• z^k + Z a' , k = 1 ^z

X

• l ^{n (} z ⁾⁺ E bvk k = 1

• ' ' E b> , k = 1 z

X

2п /

- R J⁽ ° 4= R 1 coson ° r e r = R 1

• sin ( e ) ) d e

2 п /

V y ,1

• cos ( e ) ) d e

— ^R 1 H° rr l r = R 1 • ^1Ш1 -° r e| r = r

2 n /                                                \

V x ,2 = — ^R 2 J ⁽ ° rr l r = R ₂ ^{cos (e} ) — ° r e I r = r ₂ • ^{sin (e) )} d ^e , 0

2 n                                                   \

V y ,2 = — ^R 2 J 1 ° rr l r = R ₂ • si^{n (e)+} ° r e I r = R ₂ • co^{s (e) )} d ^e , 0

V_{x , 1}, V_{y , 1} – компоненты главного вектора сил, действующих на внутреннем радиусе кольца; V_{x , 2}, V_{y , 2} – компоненты главного вектора сил, действующих на внешнем радиусе кольца.

Краевые условия на границах кольца.Определение самоуравновешивающейся нагрузки

Будем предполагать, что трение на границах кольца отсутствует (оrgl     = 0), а также rR1V R1

° rr l r — R =- Р 1 ^(e) и ° rr l r = R = - P 2 ( e ) . Исходя из краевых условий задачи и из формул для определения главных векторов сил, действующих на одной и другой границе кольца (7) и (8), получаем:

2п                                     2 п

V x J = R J P 1 ( e ) cos ( e ) d e , v , _д = R J p 1 ( e ) - sm ( e ) d e ,

2п                                       2п

V. x = R 2 J P 2 ( e ) cos ( e ) d e , v , ,2 = r 2 J p 2 ( e ) • sin ( e ) d e .

Условие самоуравновешенности нагрузок, действующих на границах кольца, определяется очевидным образом, исходя из (9):

Vx ,1 = Vy ,1 = Vx,2 = Vy,2 = 0.(10)

Будем полагать, что на внутренней и внешней границе кольца для p ₁( e ) и p ₂( e ) справедливы следующие равенства:

An X^d

P1(e) =     + E(Au •cos(j •e) + Bu •sin(j •e)),(11)

An

P 2 ( ⁹⁾ = ^,- ¹ I ⁽ A 2, j • c^{os (} j • ^{0) +} B 2, j • s^{in (} j • ⁹⁾⁾ , ²      j = 1

где A n j , B n j ( n = 1,2, j = 1, да ) - вещественные коэффициенты рядов Фурье, для которых выполнено:

1 п                                          ____ ______

A n,, =- J p n ⁽⁰⁾ ^ ^{cos (} j ⁰ d ^{0 (} n = 1,2 , j = 0, да ),                           ⁽¹²⁾

п ^J -п

1 ^п                                         ____ ______

B n,, = - J P n ⁽⁰У ^{sin (} j • ^{0) d 0 (} n = ^1,2 j = ^{1 да )} . п -п

Тогда, подставляя (11) в (9), с учетом (10), можно получить условия самоуравновешивания обеих нагрузок, действующих на внутренней и внешней поверхностях кольца. Используя известное свойство ортогональности тригонометрических функций, с учетом (11) и (12), условие (10) можно переписать в виде:

A^ = B^ = 0 , A 2,1 = B 2,1 = 0.                                  (13)

Решение первой основной задачи для упругого изотропного кольца с произвольными самоуравновешиваемыми распределениями давлений, заданными на его границах в виде рядов Фурье

Подставляя (10) в (6), можно получить:

да                        да n

Ф'(z)=E*•«1,* • z*--I*^, k=1                    k=1 z дада

' ( z ) = E k • ( k - 1> « 1 * • z^k - ² + I k ( k + 1 ) «                              (14)

k=2                               k=1            z , да                          да L v'( z ) = E b.* • k • zk-1 -I kbkk, k=1                    k=1 z

Подставляя (14) в (5), получаем выражение нормального радиального и касательного напряжений, действующих в кольце, с использованием разложений в ряд:

да                           дал

^ rr - i ^r 0=E k • «1, k ■ zk-1 -I kO+1 + k=1                      k=1 z да _____ _, 1 да л

+ I k • «1, k ■ zk-1 -I ka^ - k=1                      k=1

да

-I k •( k -!)• «1, k • zk-1 -Ik (k +1) a^ - k=2                               k =1

7k да h

I k T²: ? ^. k = 1    ^z • ^z

—

I Ь1, k " k ^+ k=1

Подставляем в (15) выражение z = r • e^{1 0} :

„                    t * - ¹-_ei⁽-^k -^-Y a²^ e- i ( ^{k +1})⁰ +

О rr  IО r 0=I * «1, * r e        I * k+1 e + k=1                                 k=1 r да _____ да п

+ Y k • «_к • r ^{k - 1} • e ^{- (} * ^{- 1 ) 0} - У *« 2^ e ^{1 (} * ^{+ 1 ) 0} -

1, k                                      k + 1

k = 1                                    k = 1     ^r

to - 2 k • ( k - 1 )• a 1, k "Г - 1	to • e - ( k ^- 2 k ( k +	^ a 2, k - i ( k + 1 ) e 1) y^1 e     -
k = 2	k = 1	r
to - 2 kbk-r - 1 k = 1	to • e - ( k + 1 ' e + 2 k- kk k = 1 r	- - ( k - 1 ) 6 e .

Задавая последовательно два значения r ( r = R 1 и r = R 2 ) в (16), получаем значение □ rr - г □ r _e на обеих границах с учетом краевых условий:

toto

- P n (g) = У k • «1 к • Rk-1 • eik-1)e - У k a    • e-(k+1)e + r n, n=1,2 V /                 1, k nk k=1                                k=1 Rn to  to

+ У k • a, _k • R ^{k - 1} • e -^{( k - 1 ) e} -У k ,, -e i^{k + 1 ) e} -

1, k n k=1                               k=1 Rn(17)

to                                                      to

-2k ■ (k -1)• aLk - R*—' • e*-1» -2k(k +1)a e—(k-1* - k=2                                       k=1           Rn toto

• -У k • b_xk • R^{k - 1} e ^{k + 1 ) e} + У k       e ^{- ( k - 1 ) e} .

• 1,    k n                                      k + 1

k = 1                                 k = 1 R n

Разделяя вещественную и мнимую части в (17), получаем очевидные уравнения:

to

- p..=n (e)=2•2 k'R.‘ "•Rek.-e(k-1,)- k=1

• - 2 1 Л N a 2, ,-e • ¹ ' ⁶ ) - k = 1 ^R n

to

-2k •(k - 1) • Rnk 1 • Re(a1, k • e-(k 1)e)- k=2

• -У kfk+l) • Re(a •e-(k+1)e)-D k+1         \ 2,k/

k = 1 ^R n

• -    2 k • R * ^{- 1} • Re ( b , - ■ e^ k -¹* ) + 2"^ ’Re (b 2 , 'e -< ^k ) )

k=1                                 k=1 Rn(18)

0 =-2k•(k-1)• r. •Im(a1,k"e k=2

-f fc¹ • Im ( a_2k•e ^{- ( k + 1 ) e} ) -

D k +1         \ 2,k/ k =1 Rn

• - 2 - • R . - ¹ • Im ( b_l .k ek ' * "'^ T k + T • ImK k e - ' k -'I k = 1                                    k = 1 ^Rn

Используя очевидные подстановки a n , _k = Re ( a n , _k ) + - • Im ( a n , _k ) , b _n , _k = Re ( b _n , _k ) + - • Im ( b _n , _k ) и e 'm ^e = cos ( m •e ) + - • sin ( m •e ) в (18) и (11) для левой части (18), можно получить две вещественные системы уравнений:

• ^-    A nT^{1 +} 2 ⁽ A n , j "^{cos (} j ^У B n , j "^{sin (} j          =

• 2        j = 1

V            ^j                                                      У n , n = 1,2

=2 • 2k • Rnk-1 •(Re (a1, k) •cos ((k-1)•e)- Im(a1, k) • sin((k-1)•e))- k=1

• ^{- 2} • 2^ - k +r • ^{( Re (} a 2, k ) • ^{cos (( k + 1 )}• ^{e ) + Im ( a} 2, k ) • ^{sin (( k + 1 )}• ^{e )) -} k = 1 ^Rn

to

• ^— E k " ^{( k —} 1 ) " ^R" ^{— 1} "  ( ^Re ( av k ) • cos (( ^{k —} ^" Ф Im ⁽ a l, k ) • sin (( ^{k —} ^"Ф

k = 2

• ^— E ^{k ( k} + ^V • ( ^Re ( a 2, k ) " cos ^{(( k + 1 )}" Ф ^{Im (} a 2, k ) " sin ^{(( k +}

  —

  
  

k = 1 R n

• ^— E k " ^Rn^{k 1} " ^{( R}e ⁽ b 1, k ) " cos ⁽⁽ k + ^{v )}"6^{) —} Im ⁽ b 1, k ) " sin ⁽⁽ k + ^{v )}" ^{e )) +}

k = 1

+ E Tk+Г " (Re(b2,k )" cos((k — О" Ф Im(b2,k )" sin((k — 0Ф k=1 Rn                                                                               (19)

0=—E k"(k—1)" Rnk1 ■ (Re(a 1, k )■ sin((k—1)"e)+Im (a1, k )■ cos((k—1)"e))— k=2

• ^— E ^{k (}„ k X¹) ■^{( —} Re ⁽ a 2, k ) ■ sin ⁽⁽ k ^{+ 1 )} " ^e)+ Im ⁽ a 2, k ) ■ cos ⁽⁽ k ^{+ 1 )} " ^{e) ) —}

k = 1 R n

• ^— E k " R nk ^{— 1} " ⁽ Re ^{( b} 1, k ) " sin ⁽⁽ k ^{+ Im (} b 1, k ) " cos ⁽⁽ k ⁺ ^"Ф

k = 1

⁺ E -^ k Tr "  ^{( — Re ( b} 2, k ) " sin ^{(( k —} ^"ф ^{Im ( b} 2, k ) " cos ^{(( k — 1 )}" ^{e) )}

k = 1 R n

Разделяем уравнения (19) для коэффициентов при cos( m • e ) и sin( m • e ) отдельно для вещественной и мнимой частей:

to

/

( AI

-jnr+E An, j • cos(j "e)|=

^V            j                          ^V n , n = 1,2

nk—1 " Re(a1,k ) + -Tkk+Г • Re(b2,k )| " cos ((k — 1) " e) RnV

—

= E 2 " k " R- k = 1 V

—

to

^— E ^k "^{( k — 1 )}" ^R n^{k 1}"^{Re ( a} 1, k ) " cos ⁽⁽ k ^—^"Ф k = 2

to

—E k=1

" ( ^{k + 3 )}" ^k

V

Rn^{k + 1}

" ^Re ⁽ a 2, k ^{) + k} "  ^R nk ^{— 1} "  ^Re ^{( b} 1, k ) | "  cos ^{(( k + 1 )} " ^e)

—

to

E B n , j " sin ⁽ j " ⁰ )

v j = ¹

\

V n , n = 1,2

to

=E

k = 1 ^V

^

——" Im(b2,k)— 2" k" Rn • Im(a1,k ) Rn +±                                   V to

" sin ((k — 1)" 0) +

+ E k "(k — 1)" Rnk 1 " Im(a1 k)" sin((k — 1)" 0) +

k = 2

to

+ E k " R. k = 1 V

'n^{k — 1} "  ^{Im ( b} 1, k ^{) — ( k + 3} + 1 ^k "  ^{Im ( a} 2, k ) | "  ^{sin (( k +} 0" ^{e) R} n             V

ю

0 = - E k • ( ^{k — 1} ) • Rn^{k — 1} " ^{Im (} a 1, k ) • cos ^{(( k — 1} ) " ⁶ ) ^- k = 2

ю

—E k=1

" k(k + 1)

D k +1

V R n

" Im ⁽ a 2, k ^{) +} k "  R nk — 1 "  ^{Im ( b} 1, k ^)| " cos ⁽⁽ k ^{+ 1} NA

ю 7

⁺ E -1 "  ^{Im ( k} 2, k ) " cos ^{(( k -} A⁶ )

k = 1 R n

ю

0 = ^— E ^k "^{( k —} 1 ) " R n^{k — 1} " ^{Re ( a} 1, k ) " sin ⁽⁽ k ^— 1 ) " ^{6 ) +} k = 2

ю

+E k=1

" ^{k ( k +} 1 )

„ k + 1

V R n

" ^{Re ( a} 2, k ^{) — k} "  R nk - 1 "  ^Re ^{( b} 1, k ) I "  sin ^{(( k + 1 )}" ^{6 ) -}

ю

^— E "  ^Re ^{( Ь} 2, k ) ' sin ^{(( k} — ^{1 )}" ⁶⁾" k = 1 R n

Выделяя уравнения для коэффициентов при одинаковых cos( m • 6) и sin( m • 6) в (20), получаем систему уравнений (ограничимся несколькими первыми слагаемыми в (6), то есть ^a 1, k ( k = 5 Ю ) = ^a 2, k ( k = 3 Ю ) = ⁰ , ^b 1,k, ( k =3,Ю ) = ^b 2, k , ( k =5,Ю ) = ^0):

Полагая j = 0 в левой части первого и второго уравнений (20), определим вещественные части коэффициентов a _1,1 и b _2,1:

² " Re ⁽ a 1,1 ) + R L. _R e ⁽ b 2_Д ) =- A l ² " ^Re ⁽ a 1,1 ) + A, " ^Re ⁽ b 2,1 ) =- ^2^, R ₂                2

Im ^{( a} _v ) = 0.

Из третьего уравнения (20):

^{Im ( b} 2,1 ⁾⁼ 0 .

Полагая j = 1 в левой части первого и второго уравнений (20), получаем систему для определения вещественной части a ₁₂, а также вещественной и мнимой части b ₂₂ для тригонометрических функций аргумента 6, учитывая условие самоуравновешенности нагрузки на внутренней и внешней границе кольца (13):

² "  R n • ^{Re ( a} 1,2 ⁾⁺ Ay "  ^{Re ( b} 2,2 ) = ^{- A} n ,1 = ⁰,

R

n

^{- 2} "  R n • ^{Im ( a} 1,2 ⁾⁺ Ay "  ^{Im ( b} 2,2 ) = ^- B n ,1 = 0.

Rn

Из третьего и четвертого уравнения (20) дополнительно получаем для тригонометрических функций аргумента 6:

—

—

² "  R n ■ ^{Im ( a} 1,2 ^{) +} Ay "  ^{Im ( b} 2,2 ) = 0 ,

Rn

² "  R n • ^{Re ( a} 1,2 ^{) —} Ay "  ^{Re ( b} 2,2 ) = 0.

Rn

Полагая j = 2 в левой части первого и второго уравнений (20), получаем систему для тригонометрических функций аргумента 2 • О:

-

-

^T • ^Re ( a 2,1 ^{) — Re} M ⁾⁺ -^

Rn                     Rn

A • I^{m (} a 2,1 ) + Im ^{( b} 1,1 ) + 3^ R_n                    R_n

" ^Re ^{( b} 2,3 ) =- ^A n ,2 ,

• M b 2,3 )=- B n ,2 .

Из третьего и четвертого уравнений (20) дополнительно получаем для тригонометрических функций аргумента 2 •О:

—

⁶ • ^Rn¹ • ^{Im (} a 1,3 ^{) —} M • ^{Im (} a 2,1 ^{) — Im ( b} 1,1 )

R

n

^{— 6} • ^Rn² • ^{Re ( a} 1,3 ^{) +} ^2 • ^{Re ( a} 2,1 ^{) — Re ( b} 1,1 )

Rn

⁺ R ^r • M b 2,3 ) = ⁰ , n

— ^3 T • ^Re ^{( b} 2,3 ) = 0 .

Rn

Полагая j = 3 в левой части первого и второго уравнений (20), получаем систему для тригонометрических функций аргумента 3 •О:

^{— 4} • ^Rn ³ • ^{Re ( a} 1,4 ^)—     . • ^{Re ( a} 2,2 ^{)— 2} • ^Rn " ^{Re ( b} 1,2 ⁾⁺ "TT • ^{Re ( b} 2,4 ) = ^{— A}n ,3 ,

Rn                          Rn

⁴ • ^Rn ³ • M a 1,4 ^)— 10T • M a 2,2 ^{)+ 2} • ^Rn • ^{Im ( b} 1,2 ⁾⁺ 45" ? • М ^Ь 2,4 ^{)= — B}n ,3 . R_n                          R_n

Из третьего и четвертого уравнений (20) дополнительно получаем для тригонометрических функций аргумента 3 • О:

—

—

" 12 • ^R n ³ • Im ^{( a} 1,4 ^{) —}     • Im ^{( a} 2,2 ^{) — 2} • ^R n • Im ^{( b} 1,2 ^{) +} ^5 • Im ^{( b} 2, k ) = ⁰

Rn                           Rn

12 • R n³ • Re ( a 1,4 ) + ^3 • Re ( a 2,2 ) — 2 • R „ • Re ( b 1,2 ) — ^? • Re ( b 2,4 ) = 0 . R_n                            R_n

Исходя из систем (21)–(28), следует, что, решив эти уравнения, можно получить выражение коэффициентов a1k(k=-), a2,k(k=12), bi,k(k=й), b2,k(k=м) через коэффициенты двух рядов Фурье (11) в следующем виде a1,1 =

A 10 • R 1

—

M R 7

,   = ^{( A} 1,0    A 2,0 )

2,1            2

•

A 2,0 • ^R 2 ^{— R} 2 ² )

R 1² • R 22

R 22 — R 1²

, a 1,2 = ⁰ ,

, b 2,2 = 0 .

Система для определения вещественной части коэффициентов при тригонометрических функциях аргумента 2 •О:

—

—

A • ^{Re (} a 2,1 ^{) — Re ( b} 1,1 ^{) +} v?

R ₁                          R ₁

R T • ^{Re (} a 2,1 ^{) — Re ( b} 1,1 ^{) +} R^

• Re ( b 2,3 ) =— A 1,2 ,

• Re ⁽ b 2,3 )     A 2,2 ,

—

6 • ^R 1² • ^{Re ( a} 1,3 ^{) +}     • ^{Re (} a 2,1 ^{) —} ReM ^{) —}     • ^{Re ( b} 2,3 ) = ⁰

R ₁                        R ₁

—

• ⁶ • ^R 2 2 • ^{Re ( a} 1,3 ^{) +} R 2y • ^{Re ( a} 2,1 ^{) — Re ( b} 1,1 ^{) —} R 3 4 • ^{Re ( b} 2,3 ) = ⁰ .

Система для определения мнимой части коэффициентов при тригонометрических функциях аргумента 2 •О:

—

—

—

—

^2 • ^{Im ( а} 2,1 ^{) + Im ( b} 1,1 ^{) +} ^4

R ₁                        R ₁

R 4 2 • ^{Im ( а} 2,1 ^{) + Im ( b} 1,1 ^{) +} r 3_

• Im ^{( b} 2,3 )      B 1,2 ,

• Im ^{( b} 2,3 )     B 2,2 ,

⁶ • R 12 • ^{Im ( a} 1,3 ) ^— ^2 • ^{Im ( a} 2,1 ) ^{— Im ( b} 1,1 ) ⁺ Т4 R ₁                        R ₁

6 • R 2² • I^{m ( a} 1,3 ^{) —} R 2y • ^{Im (} а 2,1 ^{) — Im ( b} 1,1 ^{) +} « 3 4

• Im ( ^ 2,3 ) = ⁰ ,

• Im ^{( b} 2,3 ) = ⁰ .

Система для определения вещественной части коэффициентов при тригонометрических функциях аргумента 3 •О:

—

4 • R 13 • ^{Re (} a 1,4 ^{) —} ^0 3- • ^{Re (} a 2,2 ^{) — 2} • ^R1 • ^{Re ( b} 1,2 ) R ₁

—

⁴ • ^R 2³ • ^{Re (} a 1,4 ^)— “T • ^{Re (} a 2,2 ) ^{— 2} • ^R 2 • ^{Re ( b} 1,2 ) R ₂

⁺ R

⁺ R 25

• Re ( b 2,4 ) =— ^ 1,3 ,

• Re ( b 2,4 ) =— A 2,3 ,

—

12 • R 1³ • Re ( a 1,4 )

— 12 • R 2³ • Re ( a 1,4 )

I +— з ^R 1³

+--§■

^R 2³

• Re ( a _{2 2} ) — 2 • R 1 • Re ( b 1 ₂ ) —

• Re ( a _{2 2} ) — 2 • R ₂ • Re ( b 1 ₂ ) —

4 • ^Re ^{( b} 2,4 ) = 0 , R ₁

A • ^Re ^{( b} 2,4 ) = ⁰ .

R ₂

Система для определения мнимой части коэффициентов при тригонометрических функциях аргумента 3 •О:

⁴ • R / • Im ^{( a}1₄ ^{) —} ^0 3- • Im ⁽ a 2,2 ^{) + 2} • ^R 1 • Im ^{( b} 1,2 ) R ₁

⁴ • ^R 2 ³ • ^{Im (} a 1,4 ^{) —} —у • Im ⁽ a 2,2 ^{) + 2} • ^R 2 • ^{Im ( b} 1,2 ) R ₂

4 ^R 1 ⁵ 4

^R 2 ⁵

• ^{Im ( b} 2,4 ^{) = —} B 1,3 ,

• ^{Im ( b} 2,4 ^{) = —} B 2,3 ,

^{— 12} • ^R 13 • ^{Im ( a} 1,4 ^{) —}

— 12 • R 2 • Im ( a 14 ) —

-6 3 • Im ⁽ a 2,2 ^{) —} 2 • R • Im b ^)

R ₁

-6 3 • Im ⁽ a 2,2 ^{) — 2} • ^R 2 • Im ⁽ b _1; 2 )

R ₂

⁺ R7

^R 2 ⁵

• Im ^{( b}2kk ^{) =} 0,

• Im ^{( b} 2, k ^{) = 0}.

При решении примера будем предполагать, что распределение нагрузки на внешней и внутренней границах кольца p, ^(о) (11) является четной функцией аргумента О е [ —п , п ] , то есть B n j = - в (11), (31) и (33). Это , условие приводит к тому, что все искомые коэффициенты a 1 _k ( _{k =п}) , a_{2 k} ( _k =Г2 ) , b _{l k} ( _k = 1-2 ) , b_{2 k} ( _{k l4|} являются вещественными числами и вычисляются с учетом (29) по формулам:

A^

^a 11 ^R

—

■ A 2,0 • R 2²

— R 2 ) ,

a₁₂ = 0 ,

3 • R 1² • R 22 • ( A 22 - A ₁₂) - A 12 • R 14 + A 22 • R 24

a13 _      ^Rc^

_ - 5 • A1 3 • R14 + 8 • A2,3 • R1 • R2 - 3 • A13 • R24 a 1,4 ”     8-(5 • R^ - 9 • R • R24 + 4 • R1 • R26)

a2,1 = (RI " R2 " (A2,2 - 2 • A1,2 ) + R " R24 • (A2,2 - A1,2

- R 1² • R 2⁶ • ( A_v 2 - 2 A 2,2 ) )/ 2 • ( R 1² - R 22 ) ^,

a 2,2

R 1 • R 2^ • ( 2 • A 23 • R 1 + A 1 3 • R 2 • ( - 3 • R \" + R 2~ )) 4 ' ( 5 • R 1⁶ - 9 • R 1² • R ₂ ⁴ + 4 • R ₂ ⁶ )

^b11 = ^{( R} 1⁴ • ^R 2  "^{( A} 1,2 ^{- 2} • ^A 2,2 ^{) + R} / • ^R 2 • f ² • ^A 1,2 - ^A 2,2 ^{) +}

^{+ A} 1, ₂ • ^R 1 ^{- A} 2,2 • ^R 2 /( R 1   ^{- R} 2 У ^,

3 • ( - 6 • A 2,3 • R 1³ • R 2³ + A 1,3 * ( 5 • R 1⁶ + R 2⁶ ) I 4 ^ ( 5 • R 17 - 9 • R 1³ • R ₂ ⁴ + 4 • R 1 • R ₂ ⁶ )

b 2,1

^{( A} 1,0    A 2,0 ^{1   R} 1   • ^R 2

------------------ • ----Z--------—

2 R ₂ ² - R 1^{2 ,}

b 2,2 ^{_ 0 ,}

b 2,3 ^_

44       2     2          2   2

^R 1   • ^R 2   • ⁽ A 2,2 • ^{( R} 1   ^{+ 3} • ^R 2 )   A 1,2 • ^{( 3} • ^R 1 ^{+ R} 2 ))

3 • ( R 1² - R 2² 1

b 2,4 ^_ 0 .

Зададим распределение самоуравновешивающихся положительно определенных давлений на внешней и внутренней границах кольца с помощью отрезка ряда Фурье гипотрохоиды [1]:

P1(9)_ p 2(9)_ P • J1+Л1+2 •1 • cos((1+n У9), \ V    n ! n

где Р – произвольный нормирующий множитель; n – целое число.

Коэффициенты A 1, _v _ A ₂ , _v ( j _ 0,3 ) вычисляются численно при подстановке конкретных значений Р и n в (35), а затем полученного выражения в (12) (см. рис. 2).

Подставляя далее (34) в (14), с помощью (1), (2) и (5) можно получить распределение напряжений в кольце, а с помощью (3) – распределение перемещений в декартовой системе координат (см. рис. 3).

Выводы

Впервые поставлена и решена задача для упругого изотропного кольца под действием са-моуравновешивающихся неоднородных нагрузок, действующих на его границах и представленных в виде отрезка ряда Фурье.

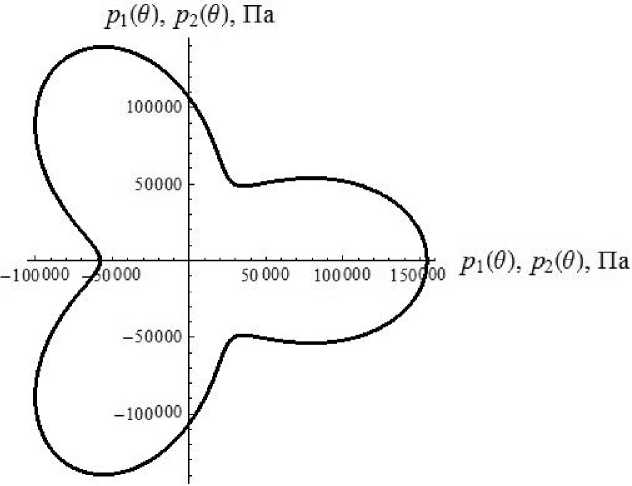
Рис. 2. Распределение приложенных к внутрен ней и внешней границе отверстия давлений приближенного в смысле отрезка ряда (11) для j = 0,3 с конкретными коэффициентами A 1, j = A 2, j , вычисленными с помощью (12) ( P = 10 5 Па, n = 2)

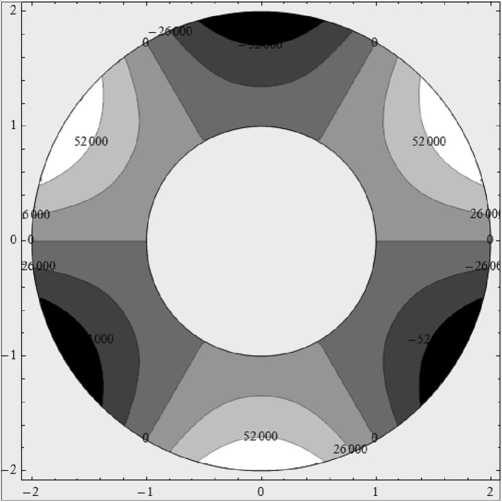
Рис. 3. Распределение касательных напряжений о r _о в кольце ( R 1 = 1, R 2 = 2, при заданных давлениях р 1 ( о ) = p ₂ ( б ) при P = 10 5 Па и n = 2 в (35) на внутренней и внешней границах)