Напряжённо-деформированное состояние и длительность до разрушения кольцевых пластин в условиях ползучести

Нормативный срок эксплуатации элементов конструкций часто отождествляют с продолжительностью времени до начала их разрушения. Отличие в оценках этого времени обусловлено использованием в расчётах разных вариантов теории ползучести, различных механизмов разрушения и критериев длительной прочности, а также видом объектов исследования [1–11]. Среди публикаций, посвященных расчёту напряжённо-деформированного состояния гибких пластин с учётом повреждаемости, можно отметить работы [6–10]. В книге [6] конечно-разностным методом исследуются пластины в геометрически линейной постановке с повреждаемостью, представляемой в виде тензора второго ранга. В [7–10] вычисления произведены с учётом геометрической нелинейности методами конечноэлементной дискретизации и R-функций в сочетании с методом Ритца. В настоящей работе на основе положений кинетической теории ползучести Работнова, учитывающей накопление повреждений в материале, найдено НДС осесимметричных кольцевых пластин двумя способами и выполнено сравнение результатов расчёта.

Первый способ, развитый в работах [12–15] применительно к вращающимся дискам, трубам, пластинам, основан на сведении задачи деформирования пластины в условиях неустановившейся ползучести к аналогичной задаче в предположении установившейся ползучести материала. При этом критерий Мизеса в определяющих уравнениях линеаризуется, что, по сути, эквивалентно использованию критерия Треска-Сен-Венана. Для того чтобы получить истинное решение, необходимо известное решение для установившейся ползучести умножить на некоторые функции координат и времени.

В основе другого способа лежит метод конечных элементов (МКЭ) комплекса ANSYS. Кроме того, в определяющие уравнения входит критерий Мизеса. Предполагается, что деформации пластины малы. Достижение параметром повреждённости критического значения при малых деформациях характерно для хрупкого разрушения.

2.    Определяющие и разрешающие соотношения

Процесс деформирования в условиях ползучести описывается соотношениями кинетической теории Ю.Н. Работнова [1, 2]:

П ki = — 1° ' ,     — = B^ ,    Ф ( ю ) = to^a (1 -ю^{а+ 1} ) m   ( k , l = 1,2,3),

°э 5°ki             ф(to)

d to = B ₂ ° ^д + dt     ф ( to )

to ( X j , 0) = 0,      to ( x * , t . ) = 1 ( j = 1,2,3).

Здесь: n _kl , ° _kl — компоненты тензоров скоростей деформаций ползучести и напряжений; W — мощность диссипируемой энергии, W = n _kl ° _kl ; ° э , ст , _э — однородные относительно напряжений функции (в качестве эквивалентного напряжения ст _э может рассматриваться или интенсивность напряжений ст i (критерий Мизеса), или максимальное касательное напряжение (критерий Треска), или другие функции; эквивалентным напряжением ст , _э может быть и ст i (критерий длительной прочности Каца), и максимальное нормальное напряжение (критерий длительной прочности Джонсона), и другие критерии); параметр to с феноменологических позиций описывает накопление повреждений в материале (для неповреждённого материала to = 0 во всех точках элемента конструкции x j ( j = 1,2,3); если в момент времени t = t , в какой-то точке x * параметр принимает значение to = 1, то будем говорить, что в этой точке тела произошло разрушение); время t = t , — это время начала разрушения тела; B 1 , B ₂, n , g , т , а — константы ползучести.

Из кинетической теории (1), (2) следуют, как частные случаи, экспериментально обоснованные теории: теория кратковременной ползучести [16], энергетический вариант теории ползучести и длительной прочности [17], теория упрочнения и различные её модификации [1, 2].

Для упрощения получения результатов выполним замену: ц = 1 -to^{a+ 1} . Тогда соотношения (1), (2) преобразуются к виду:

П _и = W 1°- ,     — = ^B '°; , ф ( ц ) = ц m (1 -ц ) ^{а ( а+ 1)}     ( k , l = 1,2,3),

°э d°ki            ф(Ц)

d p     ( а + 1) B . ° g'

=- dt         µm

p ( x j ,0) = 1,     p ( x * , t . ) = 0   ( j = 1,2,3).

Рассмотрим кольцевую пластину толщиной h при 0 <  t <  t , под действием осесимметричной нагрузки. Считаем, что в результате изгиба в пластине реализуется приближённо плоское напряжённое состояние, касательные напряжения в окружном сечении пластины учитывать не будем [18]. Системе координат O x 1 x ₂ x ₃ поставим в соответствие цилиндрическую систему координат O r ф z , в которой действуют напряжения: окружное — ст_п = °_ф , радиальное — ° ₂₂ = ° _r и перпендикулярное плоскости O r ф — ° ₃₃ = ° z = 0. Если ° _э = ° i и ° , э = ° i , то при сделанных предположениях первое из соотношений (3) представляется как

η ϕ

B 1 ° П ^{- 1} 2 ф ( р )

(2 ° ф

-° r ),

η _r

B ° n ^{- 1} n       .

—1— i — (2 ° -° ), 2 ф ( р )( r ^ф )’

η _z

B 1 ° П ^{- 1} — 2 ф ( р )

⁽ ° ф +° r ),

где

V 2          .   2

СУ - СУ СУ + СУ . ф r ф r

Второе из соотношений (3) записывается как W = р , ст ,• [2]. Отсюда для интенсивности скоростей деформаций ползучести р получаем:

П i = d е Cr /dt = В 1 ст П /ф ( ц ),

е Cr — интенсивность деформаций ползучести.

С учётом несжимаемости материала ( р _r + п_ф + n z = 0) выразим р , через компоненты тензора скоростей деформаций ползучести:

n = ² V п ф +п_Фп r +n ² /7з .

Принимая во внимание соотношения (6)-(8), находим из (5) компоненты напряжений ст_ф , ст _r :

/          N 1/ П                ,                   ..                       /          N 1/ П,

4 |Ф(ц) 1    ,!-„>(      1    1          4 U(p) 1    „.„/„f

Ст ф = з1 D I П ^{( )/} |П ф +-П r I , ст r =-1^1 n ^{( V}ln r +-П ф

3 v B1 ; v     2   ;         3 v B1 ; v

.

Предполагая, что прогибы от действия осесимметричной нагрузки малы по сравнению с толщиной пластины, в рамках гипотез Кирхгофа-Лява имеем:

V

П ф = z- = r

1 dw

^- z^- "7Г, r dr

d v n r = z^~ = dr

-

d ² w z"dr^r ’

где w — прогиб точек срединной плоскости пластины; v = v — скорость поворота нормали к срединной плоскости ( dw/dr = - v , - hj 2 <  z <  h /2, a <  r <  b , a , b — внутренний и внешний радиусы кольцевой пластины).

Интенсивности изгибающих моментов в радиальном и окружном сечениях пластины связаны с соответствующими напряжениями соотношениями:

к/ 2

hj 2

M_r = J ст _rzdz .

- hj 2

M ф = J ^СТ Ф z ^d z , - h г

Используя (10) и (11), выражения для напряжений (9) в результате ряда преобразований можно привести к виду [1, 18]:

СТф = [ф(ц)]1 n (q/D) | z |(1-n7n zMф = IMф,      стr = [ф(ц)]1 n (q/D) | z |(1-nvn zM, = lM,.

Здесь обозначено: D ( r , t ) = 2 q J [ ф ( ц ) ] ¹ n z^{( n + 1)/ n}dz , q = (2/V3)⁽ n ^{+ 1)/} n ( B 1 ) ^{- 1} n .

Уравнения равновесия тонкой круглой (кольцевой) пластины имеют вид [1, 18]:

dM  Mr - Mф

-+JL+------- = Q,    —(Qr) = - pr, dr rdr где Q(r, t) = Q(r) — интенсивность поперечной силы, действующей в окружном сечении пластины; p — интенсивность внешней равномерно распределённой постоянной нагрузки.

Примем следующие граничные условия для M_r ( r , t ) в точках, расположенных на внутренней ( r = a ) и наружной ( r = b ) кромках при 0 <  t <  t ,:

Mr (a, t) = Mr (a),     Mr (b, t) = Mr (b), где Mr (a), Mr (b) — заданные значения.

Введём обозначение Mi = ^Mф - MфMr + M2 и представим компоненты скоростей деформаций ползучести в виде:

^п ,

Vs

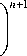
—M^{n M} , D n   d M _ф

Г 2 )n+1 zd

n r  IV3)  Dn

Система уравнений (3)-(14) позволяет рассчитать напряжённо-деформированное состояние осесимметрично нагруженных кольцевых пластин в любой момент времени вплоть до начала разрушения.

• 2.    Методики расчёта

  • 2.1.    Способ 1. Решение путём сведения задачи к аналогичной в предположении

установившейся ползучести материала

Результаты определения НДС равномерно нагретых круглых и кольцевых осесимметрично нагруженных пластин в предположении установившейся ползучести их материала достаточно хорошо известны. Использование критерия Мизеса является затруднительным, и решение в общем случае возможно только численными методами, например МКЭ. Для упрощения соответствующих вычислений квадратичный критерий Мизеса можно линеаризовать. При постоянной величине M i связь изгибающих моментов M r и M _ф друг с другом представима в виде эллипса, главные оси которого наклонены к осям координат под углом 45 ° , а контур отсекает на них отрезки, равные M i . Этот эллипс может быть заменён шестиугольником [1, 14, 18]. Тогда величина M i приближённо выражается через M r и M _ф , что эквивалентно линеаризации критерия Мизеса и переходу к критерию Треска-Сен-Венана. Важно, что величина M i зависит от местоположения точки в области эллипса. Например, если точка ( M _ф , M_r ) принадлежит области M_r >  M _ф >  0, то M i = M r ; если M _ф >  M_r >  0, то M i = M _ф ; если M _ф >  0 , M r <  0, то M i = M _ф - M r и так далее.

Рассмотрим пример, когда M i = M _ф - M_r , причём M _ф >  0 , M r <  0 . Тогда

П ф = ( 2/V3) n + ¹ z ( M ф - M r ) ⁿDⁿ , П r =- (2/V3) n + ¹ z ( M ф - M r ) ⁿDⁿ .

Из (15) следует, что п_ф+п _r = 0 . Подставляя сюда (10), можно переписать ^ ( r , t ) в виде произведения функции координат на функцию времени:

V ( r , t ) = С ( t )/ r = C ° [ X ( t ) ] " "J r = _V° [ X ( t ) ] " n ,

где C ( t ) — константа интегрирования, зависящая от времени; здесь и далее символ « о » относится к величинам, полученным из решения этой же самой задачи в предположении установившейся ползучести.

Далее необходимо выразить решение для неустановившейся ползучести как произведение решения при установившейся ползучести и функций X ( t ) и ц ( r , z , t ). Из (10), используя (16), находим скорости деформаций ползучести, а из их сопоставления с (15) получаем:

/ /— / \ (n+1)/n            ,                      ,i

M, = Mф - Mr =( Vs/2)     (С°)vnD(r, t)r-2/n [X(t)]-1.(17)

Из первого уравнения равновесия (13) с учётом заданных граничных условий для M_r на внутреннем и внешнем контурах пластины следует:

Mr (r, t) = Mr (a) + (V3/2)(n+1)/n (C°)1n [X(t)]-1 J rrD(Z, t)C-M/ndZ + Q(r),(18)

b f h/21

J j 2 J [ ф ( ц )] ^{1 n}z ^{( n + 1)/ n}dz ^ rⁿdr = JJX ( t ).

a l 0

r                           h /²                            b                            T>nj n

Здесь Q ( r ) = J Q ( Z ) d Z , J = 2 J z^{(n + 1)/ n}dz , J , = J rⁿdr , C ° = -1- ( M r ( b ) - M r ( a ) - Q ( b )). a                       0                        a                        ^JJ 1

После ряда преобразований интенсивность напряжений представляется в виде:

a = lM, = l ° Mf [ ф ( ц ) ] 1 X ( t ) = a ° [ ф ( ц ) ] 1 X ( t ),

где l и M i вычисляются согласно (12), (17); l °= | z | ^{(1 n}^ ⁿ z/J , M ° = ( M_r ( b ) - M_r ( a ) - Q ( b )) ■ r ^2/ n J 1 . Уравнение (4), учитывая выражение (3) для функции ф ( ц ), приведём к виду

J Y ( z ) dz = - [ ( m + 1) t ° ]^{- 1} J [ X ( т ) ] - ⁽ g ^{+ 1)} d т , 1                                                   0

где ^ ( z ) = z^{m ( n} - ^{g - 1)/ n} (1 - z ) ^{-a ( g + 1)/ ( n ( a+ 1) )} , t ° = [ ( a + 1)( m + 1) B ₂ a ^{f g + 1} ] " .

Таким образом, система уравнений (19), (21) есть система для определения функции времени X ( t ) и параметра повреждённости ц ( r , z , t ). Зная их, можно рассчитать НДС пластины в любой момент времени вплоть до начала разрушения. Действительно, из (16) определяется скорость ^ ( r , t ) = ^° [ X ( t ) ] ⁿ , c использованием которой из (10) вычисляются скорости деформаций ползучести

П_ф ⁽ r , z , t ) = n “ [ ^{X (} t ) ] " n , n r ^{( r} , z , t ) = n f [ ^{X (} t ) ] " ⁿ , n ° = z v7 r , n f = zd V°/ dr ,

а из (8) — n i ( r , z , t ) = n f [ X ( t ) ] n . Далее, по найденным из (17), (18) M i ., M _ф, M r рассчитывается, согласно (20), интенсивность напряжений a, ( r , z , t ) = a f [ ф ( ц ) ] 1 n/ x ( t ), а в соответствии с (12) — компоненты напряжений a_T ( r , z , t ), a _r ( r , z , t ), удовлетворяющие уравнениям равновесия. По известной функции ц выясняется время начала разрушения t * и точка с координатами r * , z * , в которой ц впервые принимает нулевое значение.

Записанные по аналогии выражения для напряжений

^а _ф ⁽ r , z , t ) ^“^( ц )^ n X ⁽ t ), a r ( r , z , t ) = a ° [ ф ( ц ) ] 1 n / X ( t ),

связанные с кинематически возможными скоростями деформаций (22) законом (9), не удовлетворяют уравнениям равновесия, однако они, как показали расчёты, в рассмотренном конкретном примере приводят к приемлемым результатам. Компоненты напряжений a“, af соответствуют решению задачи установившейся ползучести [18] и являются статически допустимыми. Компоненты напряжений (23) таковыми не являются, но если подставить (23) в (6), то получим соотношение (20). Отсюда следует, что поле (23) можно сделать статически допустимым. Для этого положим a“(r,z, t) = a“ [ф(ц)] 1 n X(t) + F(r,z, t) ar (r, z, t) = a ° [ф(ц)]1 n /X (t) + F (r, z, t)

Составляющая F ( r , z , t ) вычисляется из условия удовлетворения компонент (24) уравнениям равновесия с учётом (12) и (18):

^{F ( r} , ^z , t ) = 1 " ^^M r

JX ( t )

M r 1 1 z | ⁽¹ - ^{n )Z n} z [ ф ( ц )] 1 ⁿ .

В случае a = 0, m ^ 0, характерном для многих конструкционных сплавов, из (21) и (19) следует:

Ц =

t

1 -Z [ х-(g + 1) d * t ₀

m где в =      ------к, n + m (n - g -1)

n + m ( n - g - 1) n ( m + 1)

b f h 2 Г „ t            1P

ф i ¹ -^i X - • ^{+ 1}) d *

z ^{( n + 1)/} n dz I r ² n dr = JJ 1 X ( t ).

fl I 0 L t 0                     _

При P = 1 система (25), (26) разрешается в аналитическом виде:

X ( t ) = (1 - t/t ° )^{1/( g + 2)},

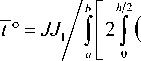
z ⁽ n ^{+ 1)/} nit ° ( r , z ) ) dz

r 2 ndr ,

[ ц ( r , z , t ) ] mn = { 1 - ( I °/ t ° ) Г 1 - ( 1 - t^ ° ) ^{1( g + 2)} _ } , t . = т °L 1 - (1 - 1 ° ft ° ) g ^{+ 2} _ .

Здесь t ° = t °(r *, z *) — время, определяемое согласно (21) и соответствующее решению при установившейся ползучести в точке, где впервые происходит разрушение. Если в ^ 1, то решение уравнения (26) можно получить численно любым из известных методов [19], например, методом Эйлера t или методом Рунге-Кутты, выполнив замену Y(t) = J X-(g+1)dт и перейдя к дифференциальному уравнению 0

по времени относительно Y ( t ).

В работе [14] отмечается, что методика прогнозирования разрушения на основе сведения задачи неустановившейся ползучести к аналогичной задаче в предположении установившейся ползучести материала может быть обобщена на элементы конструкций другого вида и вне зависимости от условий нагружения и закрепления (трубы под действием постоянного внутреннего давления, балки в условиях изгиба постоянным моментом, вращающиеся диски). Следовательно, методика применима и к расчёту НДС при ползучести пластин с различными граничными условиями и прикладываемыми нагрузками.

• 2.2.    Способ 2. Решение методом конечных элементов

При численном решении в качестве эквивалентного напряжения ст _э берётся интенсивность напряжений ст i , то есть критерий Мизеса (6). Для расчётов выбран четырёхузловой оболочечный конечный элемент SHELL181 пакета ANSYS. В силу осесимметрии рассматривается сегмент кольца в один градус с разбиением на 50 элементов вдоль радиуса и 11-точечным разбиением по толщине. Для решения системы дифференциальных уравнений по времени используется неявная схема численного интегрирования [19], а также процедура автоматического деления шага пополам.

Поскольку в моделях ползучести, встроенных в пакет ANSYS, отсутствует учёт третьей стадии ползучести, реализацию кинетической модели (1), (2) осуществляет пользовательская подпрограмма UserСreep.f, написанная на языке Фортран. Применение этой подпрограммы требует перекомпиляции пакета. Указания на запуск UserСreep.f можно найти в окне с программной документацией ANSYS Release Documentation. Для активации подпрограммы в основном программном коде служит команда TB,CREEP с параметром TBOPT=100. С помощью команды TBDATA вводятся константы материала для модели (1), (2). Вычисление значений интенсивности деформаций ползучести и параметра повреждённости в каждой точке разбиения по толщине элемента выполняется в подпрограмме UserСreep.f на основе следующей встроенной схемы:

( _е c ^r ) k ^{+ 1} = ( _е c ^r ) ^k + ( д₆ ^cr ) ^{k + 1} ,

B\ ( CT, )

(Деcr)k+1 = 1V V Дt +1, k+ к +1 ^В^ (Сk )g+1   k+1

.

to = to +--:----Л t

ф ( ю ^k )

Здесь символ к относится к величинам на к -й итерации, A t — шаг по времени.

3.    Расчёт НДС кольцевой пластины, нагруженной по внутреннему контуру изгибающим моментом

Вычисления проведены для пластины толщиной к = 0,01 м при радиусах a = 0,05 м и b = 0,1 м, безразмерный радиус р = r]а , соответственно, составляет: 1 <р< 2. По внешнему краю пластина шарнирно опёрта, внутренний край свободен от закреплений, на нём действует изгибающий момент M r ( а ) = - M = - 600 Н - м. Кроме того, M r ( b ) = 0, Q = 0, p = 0. Материал пластины имел константы, близкие к описывающим поведение сплава Д16 при температуре эксплуатации 250°С: В 1 = 3,52 - 10 ^{- 15} МПа ^- n /час ; В ₂ = 2,76 - 10 ^{- 15} МПа ^- g ^-1 /час ; n = 6; m = 8; g = 4,75; a = 0 [2, 20]. Поскольку в данном случае в = 1, можно воспользоваться аналитическим решением (27).

Рис. 1. Изолинии интенсивности напряжений с i (МПа) в сечении ф = const , 1 < р <  2 , 0 <  z <  к/ 2 : вычисленные согласно (20), (27) при t = 0( а ) и t * = 4,59 - 10⁴ час ( б ); полученные МКЭ при t * = 8,46 - 10⁴ час ( в )

На рисунке 1 представлены изолинии интенсивности напряжений с i в сечениях {1 < р <  2, 0 <  z <  к /2}, отвечающие решению задачи в предположении установившейся ползучести при t = 0 и в момент времени t . = 4,59 - 10⁴ час, рассчитанные по формулам (20), (27), а также при t . = 8,46 - 10⁴ час, полученные численным методом. Результаты расчётов показывают, что в процессе ползучести в пластине идёт непрерывный процесс перераспределения напряжений и накопления повреждений в материале. Очевидно, что опасное сечение — это { р = 1, z = к /2}. Именно отсюда с момента t * начинает распространяться разрушение.

а,р, МПа                                                    а, , МПа

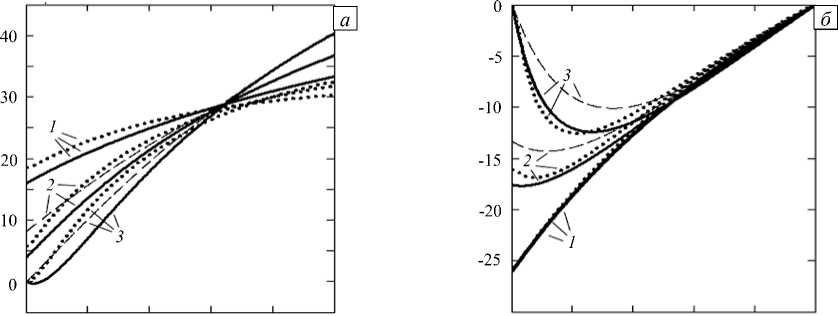
Рис. 2. Зависимость с_ф ( а ) и с r ( б ) от р при z = к] 2 : сплошные и штриховые линии - расчёт по (12) и (23) соответственно; пунктирные линии - расчёт МКЭ

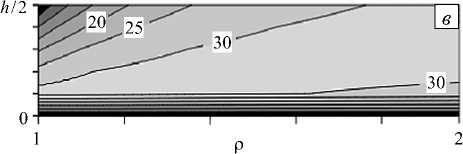
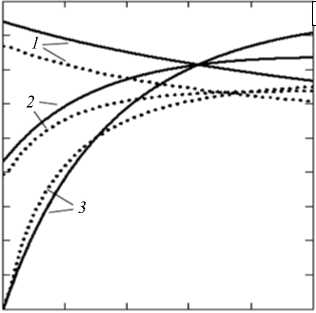
На рисунке 2 сплошными и штриховыми линиями показаны распределения компонент σ_ϕ , σ _r в сечении {1 ≤ρ≤ 2, z = hI 2} , рассчитанные по (12) и (23) соответственно. Цифрами обозначены линии для t = 0 (линии 1 ); 4,0 ⋅ 10 ⁴ час (линии 2 ) и t _* = 4,59 ⋅ 10⁴ час (линии 3 ) (линии 1 , штриховая и сплошная, совпадают). Напряжения (23), связанные с кинематически возможными скоростями деформаций ползучести, можно использовать в качестве верхней оценки. На этом же рисунке пунктирными линиями 1 , 2 и 3 изображены аналогичные результаты для компонент напряжений, рассчитанных МКЭ в моменты времени t = 0 , 7, 0 ⋅ 10 ⁴ час и t _* = 8, 46 ⋅ 10 ⁴ час.

На рисунке 3 а сплошными и пунктирными линиями изображены зависимости интенсивности напряжений σ _i (соответствующие компоненты σ_ϕ и σ _r см. на рисунке 2) при z = hI 2 от ρ , вычисленные по (20) и МКЭ. В целом картина распределения напряжений, полученных 1-м способом, близка к результатам 2-го — численного, способа расчёта. Рисунок 3 б содержит рассчитанные МКЭ зависимости

<3; , МПа

о,, МПа 40

⁴ t, час ⁶

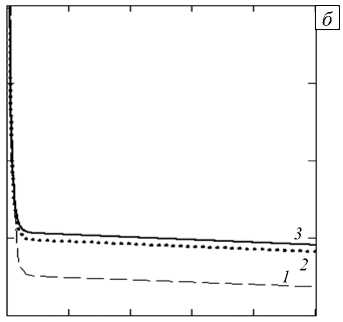
Рис. 3. Зависимости интенсивности напряжений σ _i (соответствующие компоненты σ_ϕ и σ _r см. на рисунке 2) в сечении z = h /2 от ρ ( а ) и от времени при ρ= 1 и различном шаге интегрирования по времени ( б ); на ( а ) сплошные линии соответствуют расчёту по (20), пунктирные – расчёту МКЭ; на ( б ) максимальному шагу интегрирования 5, 2, 1 час отвечают линии 1 , 2 , 3

интенсивности напряжений при { ρ= 1, z = h /2} от времени при максимальном шаге интегрирования на установившейся стадии ползучести, равном 5, 2, 1 час (см. линии 1 , 2 , 3 соответственно. Отличие интенсивностей напряжений в момент времени t = 10 ⁴ час при шагах 5 час и 1 час (см. линии 1 и 3 ) составляет 0,7%, а при шагах 2 час и 1 час (см. линии 2 и 3 ) — 0,1%. При этом время до разрушения t _*

In М

9     10    11     12     13     14 1пЛ

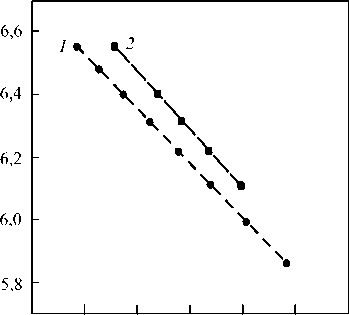
Рис. 4. Зависимость времени начала разрушения t _* от величины изгибающего момента M , приложенного на внутреннем контуре пластины: расчёт по (27) (линия 1 ) и МКЭ ( 2 )

отличается, соответственно, на 18% и 3%. При уменьшении максимального шага интегрирования время t _* уменьшается и стремится к некоторому предельному значению, однако при этом существенно возрастает общее время счёта. На всех рисунках, за исключением рисунка 3 б , графики построены по результатам расчётов МКЭ с максимальным шагом интегрирования 2 часа.

На рисунке 4 демонстрируются зависимости времени начала разрушения t _* от величины изгибающего момента M , приложенного на внутреннем радиусе пластины, в логарифмических координатах. Линии 1 и 2 относятся к результатам, полученным 1-м и 2-м способами. Используя эти прямые линии (или их продолжение), можно прогнозировать время начала разрушения при различных значениях приложенной нагрузки. На диаграмме видно, что применение критерия Треска–Сен-Венана (линия 1 ) даёт нижнюю оценку времени начала разрушения конструкции.

4.    Заключение

Для задачи изгиба кольцевой пластины моментом, приложенным на внутреннем контуре, время начала разрушения, вычисленное с применением критерия Мизеса, почти в два раза больше времени, полученного с использованием критерия Треска–Сен-Венана. Однако упрощенный способ расчёта позволяет прогнозировать зачастую интересующую расчётчиков нижнюю оценку времени начала разрушения. Окончательный выбор критерия должен определяться в результате экспериментальных исследований.

Следует отметить также, что методика прогнозирования разрушения на основе упрощённого способа расчёта напряжённо-деформированного состояния с учётом накопления повреждений, опирающегося на решение в предположении установившейся ползучести, может быть применена к пластинам с различными условиями нагружения и закрепления.

Работа выполнена при финансовой поддержке Программы фундаментальных исследований СО РАН III.23.3. (проект III.23.3.2.) и РФФИ (проект № 15-01-07631-а).