Настраиваемая (универсальная) градусная гномоническая сетка

Со времен фламандца Герарда Меркатора в картографии получил распространение единый координатный способ определения географического места на Земле — система параллелей и меридианов. Удобство ее использования связано с тем, что локально в любой точке на сфере меридианы и параллели пересекаются под прямым углом. Это свойство ортогональной системы координат изотропного двумерного пространства представляется совершенно естественным. Однако воспроизведение криволинейной поверхности Земли на плоской карте является сложной задачей, которая решается разными способами. Обычно авторы карт стараются реализовать принцип равенства изображаемых площадей (равновеликая проекция) или равенства углов между направлениями (равноугольная проекция). В обоих случаях форма фигуры на плоской карте всегда и неизбежно искажается. При составлении карт участков поверхности Земли используются обычно азимутальные проекции: плоские, цилиндрические, конические. Плоские проекции в свою очередь подразделяются на гномоническую, стереографическую и ортографическую. Особое место в картографии занимает плоская проекция Ламберта, позволяющая получить изображение целого полушария Земли. В ней максимально сохраняется площадь фигуры, но ее форма и углы между направлениями нарушаются. Первая физическая карта Земли (с двумя полушариями), с которой знакомятся еще в школе, выполнена в проекции Ламберта.

В кристаллографии изображение на плоскости полярного комплекса кристалла — пучка нормалей к плоским сеткам или направлений, имеющих определенное структурное значение, представляется более простой задачей, чем в картографии. Здесь применяется та же локально ортогональная система координат — градусная сетка полярного и азимутального углов (параллели и меридианы) [1, 2]. Поскольку сфера в кристаллографии условна, форма фигуры, вырезаемой системой нормалей на ней, и ее площадь не имеют большого значения. Главным показателем в кристаллографии являются угловые расстояния между направлениями и ориентация центральных сечений.

Чаще всего в кристаллографии применяют стереографическую проекцию, позволяющую в пределах одного круга изобразить весь полярный комплекс кристалла. Однако достигаемая при этом полнота изображения, по нашему мнению, не компенсирует недостаток ясности в восприятии кристаллографического содержания проекции. Так, на- пример, набор граней кристалла, представляющий единую кристаллографическую зону (грани призмы), на стереографической проекции проецируется на линию дуги. Похожей дугой изображается серия граней пирамиды. Отличить эти дуги не всегда просто, и здесь решающее значение имеет правильная кристаллографическая установка кристалла. Поэтому чрезмерно большое значение в кристаллографии придается правильной установке кристалла. Второй недостаток стереографической проекции связан с необходимостью проведения определенных и не всегда простых расчетов при поиске индексов направлений или граней.

Стереографическая проекция алгебраически представляет собой преобразование угловых параметров ρ и ϕ (полярного и азимутального углов) ориентации вектора в линейные параметры X , Y на плоскости:

cospsincp             sinp l + cospcos

где R — радиус условной сферы проекции.

Большое удобство в работе со стереографической проекцией дает широко известная градусная сетка Вульфа (экваториальная проекция), которую можно построить по формулам (1). При использо-

вании сетки Вульфа принимается обычно R = 100 мм, а разрешение по углам ρ и ϕ составляет 2°.

Сетку Болдырева — разновидность полярной проекции градусной сетки в стереографической проекции — легче представить в полярных координатах ( r , α ):

„ sinp

, α = ϕ. (2) 1 + cosp

Широко известная сетка Федорова является комбинацией двух повернутых на 90° относительно друг друга сеток Вульфа и одной сетки Болдырева [1]. Разрешение сеток по Е. С. Федорову составляет 5°.

Важно отметить, что упомянутая выше проекция Ламберта обладает теми же достоинствами и недостатками, что и стереографическая проекция. Тем не менее она не прижилась в кристаллографии, но используется в других науках о Земле, в частности в тектонике при описании формы залегания земных пород. Проекция Ламберта получается с помощью преобразований

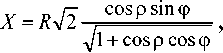
(3) д/1 + COS р COS ф

Для удобства работы с ней используется градусная сетка Шмидта (экваториальная проекция), рассчитываемая по формулам (3). Сопоставив уравнения (1) и (3), можно убедиться, что сетки Вульфа и Шмидта должны быть весьма похожи, включая и одинаковые области допустимых значений углов. Однако стереографическая проекция является равноугольной, а Ламберта — равновеликой. Других преимуществ у стереографической проекции по сравнению с проекцией Ламберта нет.

Плоская гномоническая проекция [1, 3] в кристаллографии используется не так часто, как стереографическая. Важнейшим ее недостатком является неограниченность на плоскости проекции, что на практике приводит к уменьшению области значений отображаемых углов ρ и ϕ. Эта особенность для высокосимметричных кристаллов оказывается несущественной, поскольку фундаментальная область кристалла воспроизводится на весьма небольшой площади гномонической проекции. Так, например, фундаментальная область кристалла алмаза симметрии m3m ограничивается небольшим телесным углом π/12, в который попадают по одной грани все возможные для алмаза кристаллографические простые формы. То есть фундаментальную область кристалла алмаза можно выделить на гномонической проекции треугольником с вершинами в точках [010], [011] и [111].

Преобразование угловых координат кристаллографических направлений в линейные на гномонической проекции производится по формулам

. (4)

С помощью уравнений (4) можно построить координатную сетку Хилтона весьма удобную для использования на практике. Она относится к сеткам экваториального типа. Дуги всех больших кругов (экватора и меридианов) на гномонической проекции всегда представляются прямыми линиями.

Важнейшим преимуществом гномонической проекции является то, что грани одной кристаллографической зоны лежат на одной прямой в плоскости проекции. Поэтому расчет кристаллографических индексов граней весьма прост и определяется системой одинаковых линейных уравнений. Так, если две грани с индексами (h₁ k₁ l₁) и (h₂ k₂ l₂) принадлежат к одной кристаллографической зоне, то грань с индексами ( a h₁+ b h₂, a k₁+ b k₂, a l₁+ b l₂), где a и b любые целые числа, тоже будет относиться к этой зоне.

Для расчета индексов Миллера граней и индексов Вейсса для векторов можно использовать правило равных отрезков. Например, грани (010), (041), (021), (011), принадлежащие к одной зоне и располагающиеся на прямой, последовательно отстоят друг от друга через одинаковые отрезки — 12.5 мм ( R = 50 мм) в согласии с линейно увеличивающимся третьим индексом l . Данное правило является следствием свойств тригонометрической функции тангенса, используемой как при расчете кристаллографических индексов, так и в гномонической проекции, преобразующей угловые величины в линейные отрезки (формулы 4).

Второе, не менее важное преимущество заключается в том, что гномоническая проекция полярного комплекса нормалей к граням кристалла получается автоматически при отражении световых рефлексов от кристалла дополнительно в параболоиде вращения. Кристалл должен располагаться при этом в фокусе параболоида.

Эта особенность гномонической проекции реализована в параболическом гониометре [3]. Для практических целей удобно использовать сетку Хилтона с ценой деления в 2°, начерченную на листе бумаги со стандартным радиусом сферы R = 50 мм. А. И. Глазовым в работе «Методы морфометрии кристаллов» [3]

достаточно подробно изложены приемы работы с сеткой Хилтона.

На рис. 1 приведена настраиваемая градусная гномоническая сетка, образующаяся при повороте полярной оси сферы (рис. 2) в плоскости нулевого азимутального угла (нулевого меридиана) на полярный (широтный) угол α , равный 35°16', относительно плоскости проекции. Он соответствует углу между осями симметрии второго и третьего порядков в кубических кристаллах. Такую сетку можно называть «алмазной».

Расчет координатной сетки для гномонической проекции с заданным полярным углом α можно произвести по формулам:

X = Л sin ф/(cos a cos ф-sin а /gp),

. (5)

Настраиваемая сетка позволяет осуществлять те же измерения углов, что и сетка Хилтона. Создание особой градусной сетки с заданным углом α чаще всего необходимо при неправильной ориентации кристалла в параболическом гониометре, для поиска двойников кристаллов или получения особых проекций криволинейных поверхностей кристаллов. Правильная установка кристалла при изучении его морфологии с применением настраиваемой сетки становится необязательной.

Покажем на примере алмаза преимущество настраиваемой градусной гномонической сетки. С помощью алмазной координатной сетки (рис. 1) можно непосредственно продемонстрировать особенности ориентации конусов второго типа по И. И. Шафрановскому [4] (рис. 3, а). Конусы первого типа хорошо видны на фоне экваториальной сетки

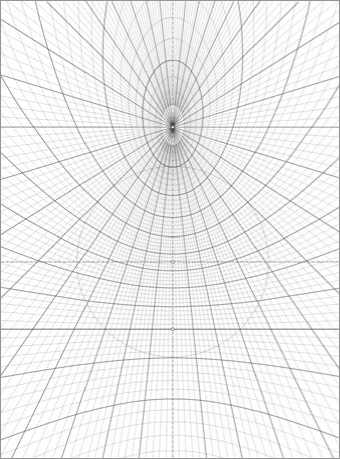
Рис. 1. Алмазная гномоническая градусная сетка

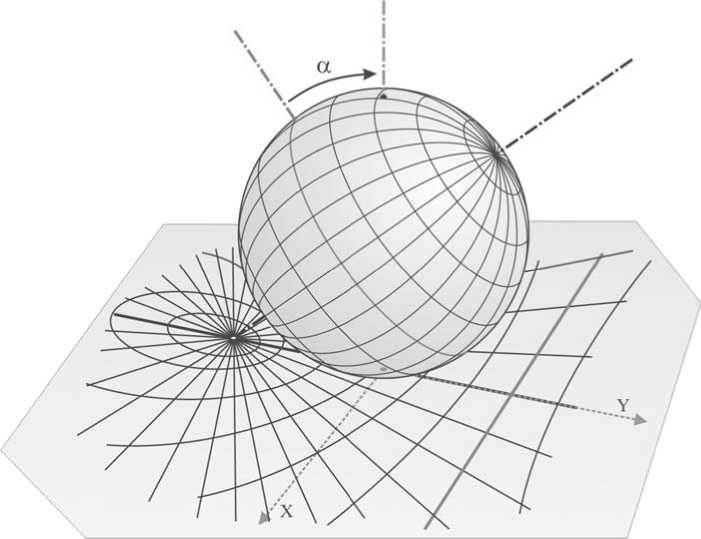
Рис. 2. Построение настраиваемой гномонической градусной сетки

Хилтона (рис. 3, б). С помощью алмазной сетки легко выявляются кристаллографически значимые по мнению А. А. Кухаренко [5] структурные зоны на алмазах уральского типа, содержащие также грань октаэдра (рис. 4).

Удобство применения алмазной сетки проявляется и при настройке кристалла алмаза в гониометре. Часто одна из граней октаэдра присутствует на кристаллах алмаза, и ее легко ориентировать по оси алмазной сетки при поиске правильной кристаллографической установки кристалла. В алмазной сетке можно без труда выявить многие закономерности структуры кубического кристалла.

Иногда двойники алмаза (по шпинелевому закону) добавляют группу особых, нехарактерных для первого субиндивида рефлексов на экране параболического гониометра.

Шпинелевые двойники в алмазе диагностируются достаточно просто с помощью другой координатной сетки с углом α, равным 74°12'. Известно, что минимальный угол между четверной осью одного субиндивида и ближайшей к ней тройной осью другого, находящегося в двойниковом положении, достигает 15°48'. Установку двойникового сростка кристаллов в гониометре производят по четверной оси одного из субиндивидов. Путем поворота кристалла вокруг оптической оси прибора тройную ось второго субиндивида следует отнести в первую четверть гномонической проекции (рис. 5, а) так, чтобы ось третьего порядка второго кристалла располагалась строго на линии тетрагонтриоктаэдров, соединяющей точки [010] и [111] первого кристал- ла. В данном случае ось третьего порядка двойника совпадет с осью «шпинелевой» градусной сетки. Цена делений сетки, изображенной на рис. 5, а, составляет 10°. При этом полюс кристаллографической проекции, совпадающий с направлением [010] структуры первого субиндивида, будет расположен на нулевом меридиане градусной сетки на угловом расстоянии в 15°48' от тройной оси второго кристалла. С помощью такой сетки легко разделить рефлексы субиндивидов. Рефлексы от поверхностей первого субиндивида отмечены более светлым оттенком.

Если ось сетки располагается по линии, соединяющей точки [010] и (111) первого кристалла в правильной кристаллографической установке, то на 0, 120 и 240-м меридианах сетки находятся точки, отражающие направления [010], [011] и [110] структуры первого кристалла (отсчет углов ведется против часовой стрелки). Одновременно для второго кристалла эти меридианы совпадают с линиями тригонтриоктаэдров. В частности, три ближайшие точки структурной сетки ромбододекаэдра {110} второго кристалла алмаза лежат на этих меридианах на широте 35°16', отсчитываемой от полюса. Две точки, связанные с меридианами 120 и 240°, совпадают с точками [011] и [110] первого кристалла (отмечены крестиками на гномонической проекции; рис. 5, а), а третья точка должна располагаться по другую сторону от полюса проекции на нулевом меридиане в третьей четверти. Местоположение ее легко можно найти по градусной сетке.

Интересно отметить, что на округлых двойниковых сростках кристаллов алмаза из бразильских и якутских россыпей часто обнаруживаются плоские участки тетрагонтриоктаэдра (121) (рис. 5, 6), грани которого являются S-гранями алмаза согласно теории Хартмана-Пердока (Hartman, Perdok) [6, 7]. Вследствие симметрии двойникования алмаза у двух субиндивидов плоские сетки — (121) и центрально симметричная ей — совпадают. Эти грани ориентированы перпендикулярно плоскости двойникования субиндивидов. Наличие дополнительной, кроме октаэдрической, плоской грани (121) на округлых кристаллах, очевидно, связано с их двойникованием. Определенную роль при этом могли играть и пластические деформации кристалла алмаза, наблюдаемые на фотографии его поверхности (рис. 5, б).

С другой стороны, двойниковый шов можно считать фрагментом структуры гексагонального лонсдейлита, когерентно сросшегося плоской сеткой (001) с гранью (111) кубического алмаза. В этом случае одна из плоских сеток {121} алмаза, наблюдаемая на гномограмме, должна совпасть с одной из граней {100} лен-сдейлита. Но грани простой формы {100} лонсдейлита согласно теории периодических цепей химических связей Хартма-на-Пердока можно отнести к F-граням, поскольку они содержат три цепи силь-

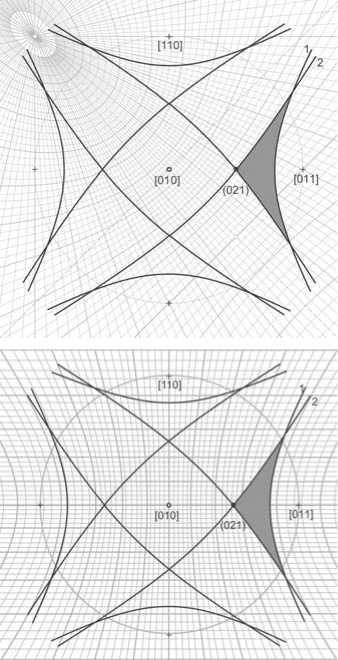
Рис. 3. Гномоническая проекция конусов двух типов на кристалле алмаза уральского типа. Фоном служит алмазная гномоническая градусная сетка (а) и сетка Хилтона (б)

6—

<0Ю)

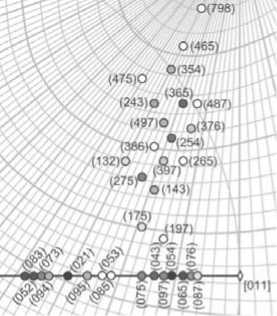
Рис. 4. Распределение значимых плоских сеток на треугольном рефлексе алмаза уральского типа. Фон — алмазная гномоническая координатная сетка

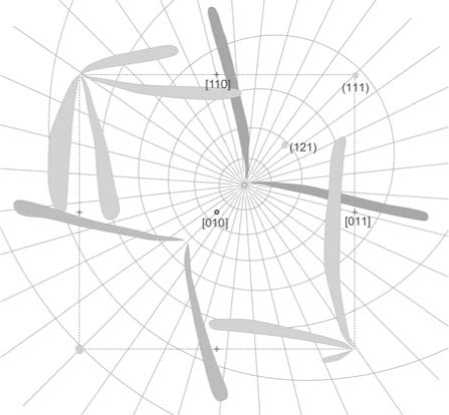
Рис. 6. Гномограмма рефлексов трех соседних субиндивидов в сложном двойнике алмаза из якутской коллекции. Фон — шпинелевая координатная сетка

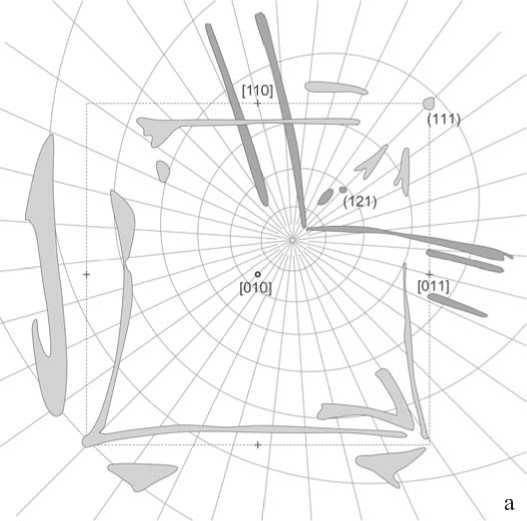
Рис. 5. Сдвойникованный округлый кристалл алмаза № 10-5 из бразильской коллекции алмазов бассейна р. Макаубас (штат Минас Же-райс): а — гномограмма (фоном служит шпинелевая координатная сетка), б — фотография поверхности кристалла вблизи двойникового шва

ных связей, что позволяет считать простую форму {100} лонсдейлита габитусной. Если бы лонсдейлит встречался в природе в виде монокристалла, F-грани {100} могли бы определять облик кристалла совместно с F-гранями {001}. Однако в научной литературе сведения о самостоятельной форме монокристалла лонсдейлита не приводились. Известно только, что лонсдейлит рентгенографически всегда обнаруживается в срастании с алмазом.

В этой связи плоский участок грани (121) на двойниках алмаза (рис. 5, 6) с большим основанием можно считать поверхностью габитусной грани (100) мо-нокристального блока лонсдейлита, находящегося в эпитаксиальном срастании с алмазом в области двойникового шва, а лонсдейлит представляет собой закономерный полисинтетический двойник алмаза.

Таким образом, настраиваемая градусная гномоническая сетка может оказать существенную помощь в морфологических исследованиях при использовании параболического гониометра и в теоретических кристаллографических расчетах.

Работа выполнена при частичной финансовой поддержке программ Президиума РАН № 27 (09-П-5-1028) и ОНЗ РАН (09-С-5-1022).