Nature-inspired optimal tuning of scaling factors of mamdani fuzzy model for intelligent feed dispensing system

Published Online September 2018 in MECS

Nature-inspired algorithms have come a long way in the optimization of different industrial processes with their flexibility in solving nonlinear optimization problems. With their increasing popularity in industrial applications, more research works have been channeled towards their implementation. An engineer proposes up a new idea and then uses optimization to improve on that idea by carrying out variations on an initial concept and using the information gained to improve on the idea for better results. Optimization problems can be seen in many areas such as manufacturing systems, economics, physical sciences, and computational systems. In the past years, several optimization methods have been developed based on the nature inspired analogy. In spite of the fact that these are used in solving problems, there are yet to be methods used to know the optimal parameters in finding solutions to problems that can be set from the start when these algorithms are used. This has made researchers to combine two or more intelligent techniques so as to achieve better results [1]. A good example is the integration of fuzzy logic and Genetic algorithm to provide optimal solution within a logical time boundaries.

Existing Poultry Feed Dispensing Systems (PFDS) in literature [2] - [4], mainly apply the use of a single nature-inspired technique in solving the problems of slow system response and undesired stability. These previous works made use of Genetic algorithm on Proportional Integral Derivative (PID), Fuzzy logic on PID, and Particle Swarm Optimization on PID. Due to some of the existing challenges of system stability and response in these PFDS, the concept of applying the notion of hybrid nature-inspired algorithms is hereby proposed in this work. One of the rationales in the application of hybrid intelligent system is their ability to complement the weaknesses of a single intelligent technique thereby producing the best results.

The PID controller has been proven satisfactory as applied to wide range of industrial control systems. It can be used to control many processes in as much as it has measurable output, a known ideal value for the output and an input value to the process [5]. Classically tuning PID controller could produce system response, but its application is bound to experience poor performance when it is introduced to high dimensional and time varying systems [6]. This will lack robustness and undesirable results in the percentage overshoot, rise time and settling time from the closed loop system model. This is contrary to the hybrid intelligent techniques which provide effective and satisfactory performance when these specifications are considered.

The remaining part of this paper is organized into section. Section two presents a review of two nature-inspired optimization algorithms, GA and PSO. It also gives a description of the conventional PID controller and the Fuzzy Logic Controller (FLC). Section three presents the brief mathematical modeling of the conceptualized PFDS, tuning of PID controller using GA and PSO, and the optimization of the scaling factors of the FLC using PSO. Section four gives the simulated results obtained from the MATLAD/SIMULINK r2015b environment. Lastly, section five presents the conclusion of the paper.

• II.    Review of Nature-Inspired Optimization Algorithms and PID Controller

Some classes of optimization techniques which have come into play during the last decades are mainly nature-inspired algorithms. Two of these nature-inspired algorithms are Genetic Algorithm and Particle Swarm Optimization algorithm. Apart from the well known Genetic and Particle Swarm Optimization algorithms, others include Bat algorithm, Cuckoo search, Ant Colony algorithm, Firefly algorithm, and Bee algorithm. Genetic algorithm can be outlined as evolutionary method which imitates in some sense the mechanisms of evolution such as sexual reproduction, selection, mutation and crossover [5]. Similar to other evolutionary computation algorithms like GA, is PSO which is a population-based iterative algorithm. It is initialized with a group of random particles (solutions) and then searches for optimum by updating generations. In every new generation, each particle is updated by two "best" values. The first one is the best solution which it has achieved so far and it is called pbest . The other best value is the global best in the whole swarm and it is called gbest . After finding the two best values, the particle updates its velocity and positions [7].

• A.    Genetic Algorithm

Genetic algorithm which is based on the principle of selection, reproduction, mutation and crossover, randomly generates a population, selects individuals from that population to be parents and uses those parents to produce children for subsequent generations. The population thus evolves towards an optimal solution [8]. The GA technique has some limitations as it suffers from premature conversion and is not efficient in solving large optimization problems [9]. The calculation complexity of mutation, selection and cross over happen to be a form of limitation, but gets better with time. GA proceeds in an iterative manner by generating new populations of individuals from the previous [10]. Fig. 1 shows the flowchart diagram of GA.

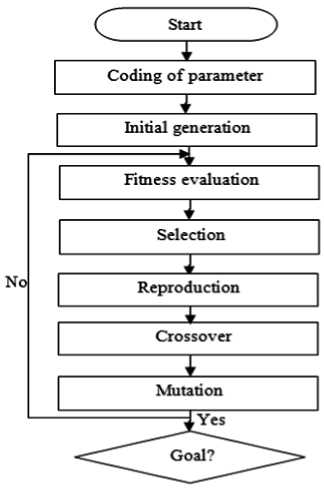
Fig.1. Flow chart of the genetic algorithm [11]

The basic GA algorithm is given as follows:

• 1.    Randomly generate a population of binary string.

• 2.    For each string in the population, calculate its fitness.

• 3.    Generate or produce offspring strings using the process of reproduction, crossover and mutation.

• 4.    Evaluate and calculate the fitness of each string or chromosome.

• 5.    If the optimum goal is achieved or the maximum number of generations is produced, return the best string (chromosome) as the solution, or else go to step 3.

• B.    Particle Swarm Optimization (PSO)

Particle Swarm Optimization Algorithm was introduced by Kennedy and Eberhart in 1995. It is one of the most important swarm intelligence [12]. It is based on the stochastic optimization technique that is inspired by the behaviour of fish schooling and bird flocking. The concept of using PSO is motivated from the simulation of this social behaviour [10]. A swarm is made up of m particles moving in the D dimension at a particular speed. Where m is the size of the population, while the position of ith particle is given by x_i = x_i1,x_i2,x_i3,x_i4, — x_lD , with 1< i <  m . The speed of the ith particle is v _i = V_i1, V_i2, V_i 3 , V_i4, — v_iD, where D is the dimension of the search space and 1< i < D . The best position for the ith particle denoted by    P best    is given by

P_i = P_i1,P_i2,P_i3, P_i4, -.,P_iD ; and the best global position for the swarm denoted by g bes _t is given by P_g = P_g i ,P g2 ,P g3 , — ,P im , where g E {1,2,—, m}. The speed and the position of the particle can then be updated as depicted in Fig. 2.

The pseudo code for the PSO procedure is given as follows:

• 10:    initialize_particle_randomly;

• 20:    while termination_condition_not_meet do

• 30:    evaluate_each_particle_solution;

• 40:    replace_worse_local_best_solutions;

• 50:    find_the_global_best_solution;

• 60:    generate_new_particle_solutions;

• 70:    end while [13]

Each particle in Fig. 2 represents a potential solution or a candidate solution to the optimization problem. It moves to a new position according to the new velocity which includes its previous velocity and moving vectors according to the previous best solution and global best solution; with each particle moving not only in the direction of the local best solution, but of the global position. The best solution obtained is then kept. If a particular particle discovers a new possible solution, other particles will move closer to it in other to explore the region [14]. The biggest characteristic of PSO is in its simple structure, fast convergence, and its ability to prevent falling into a local optimum solution. At the same time, PSO is a random algorithm with a parallel structure [10].

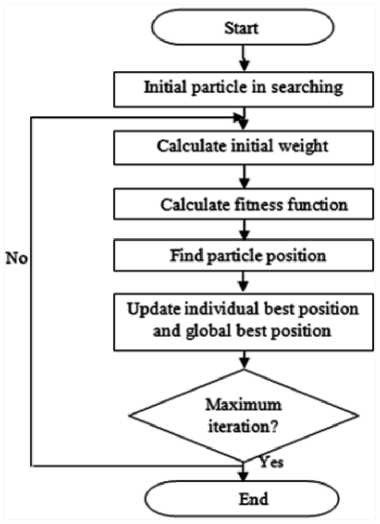
Fig.2. Flowchart for PSO [4]

• C.    Conventional PID Controller

The PID controller is made up of the proportional gain scaling factor (kp), the integral gain scaling factor (k[) and the derivative gain scaling factor (kd). The PID controller is used because of its simple control structure which gives better sensitivity, increases the overall stability of the closed-loop system and the provision of a reduced overshoot [8]. The proportional control will affect the reduction in the rise time and steady-state error. The integral factor eliminates the steady-state error and making the controller to have a pole at s = 0 [15], but provides an undesirable transient response. The derivative scaling factor improves the transient response, reduces the overshoot, and increases the stability of the system. In the time domain, the controller can be represented as

u(t) = kpe(t) + kt J0£e(t) dt + kd ^) (1)

The proportional gain factor is summed up with the sum of the integral and the derivative gain factor after they have been passed through their respective block as depicted in Fig. 3. The output from this summation is used as an input to the plant. The expected speed is set to a unit constant, serving as a step to the system. The error value and control signal to the plant are monitored from different connected scopes.

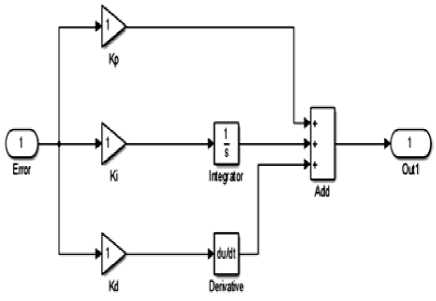
Fig.3. PID controller subsystem

The transfer function of the PID controller is given as

G(s) = ^^ = КР + - + Kd s v J    E(S)     P     S      a

where

Tt(integral time constant) = kp / /K

Td (derivative time constant") =

K/

/ ^K _?

• D.    Fuzzy Logic Controller (FLC)

The fuzzy logic controller is an error feedback controller. The proposition of the fuzzy logic controller (FLC) is to get a better performance in the conventional PID controller. Fuzzy Logic Controller was incorporated into the PFDS due to its efficacy to deal with uncertainties thereby stabilizing the system during transients between operating points. For fuzzification, the Mamdani inference system was used, because of its simplicity in a nonlinear closed loop control system.

In order to define the lower and upper limits for the model, the triangular membership function was used. This brought about precision in defining the fuzzy sets. The fuzzifier carries out the process of fuzzification of the set of the error and change in error inputs, since most physical systems cannot interbreed fuzzy sets [16].

Whereas the rule base and inference engine were used to provide the control rules, the defuzzifier produced the final crisp value for the output linguistic variable. Tuning the scaling factor gave a better effect on the control performance.

• III.    Related Works

Over the years, interests had been shown in the design and development of poultry feed dispensing systems. These works have explored the need to use intelligent techniques, from fuzzy logic to nature- inspired swarm intelligence to tune some useful FLC parameters. The tuning of these parameters is one of the major prerequisites in the application of a fuzzy logic controller.

The design of a mobile poultry liquid feed dispensing system in [2], used Genetic Algorithm to tuned a PID controller which controlled the movement and release of liquid feed in a defined pattern to avoid contamination. The results showed a better performance than the system implemented without a nature-inspired control technique [3]. Notwithstanding, this system is incapable of dispensing solid feed. Although another was further designed in [4], to dispense both solid and liquid feed, reducing contamination and the unusual human involvement, proposition in [4] lacked the desired robustness in the system performance.

This work principally aimed to obtain a dynamic model better than the existing ones where the response is faster, steady state error is eliminated, rise and settling time is quickly achieved, and the percentage overshoot is truncated to a desired minimum.

• IV.    Mathematical Modeling of Poultry Feed Dispensing System

The conceptualized PFDS is made up of two subsystems, the solid feed subsystem and the liquid feed subsystem. The solid feed subsystem was designed to convey and dispense the feed by controlling the DC motor from the control unit. The liquid feed subsystem comprises of the liquid a tank and pipe which conveys the liquid to the trough. Fig. 4 and 5 show the main view and close loop representation of the intelligent poultry feed dispensing system. Detailed mathematical modeling of both the liquid and solid subsystem is as provided in [17]. The overall transfer function of the conceptualized PFDS is as provide in (3).

G(s) =

/2(s) йй

S2 + 126.5S+278.1

• A.    Tuning of PID Controller

There are many ways to tune the controller parameters of a PID controller. Some of these methods include the Ziegler-Nichols’ method, the Good Gain’s method, Skogestad’s method and the intelligent tuning methods. In all these tuning method, the main aim is to obtain for any dynamic system, better stability and fast response.

But for this work, the research aims to investigate the intelligent tuning methods on PID controller using GA and PSO. This research work expects to see which between the two optimization techniques will produce better stability and faster response under some performance indices.

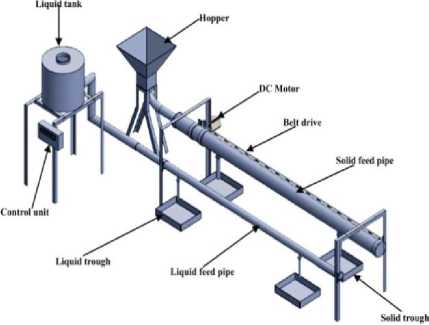
Fig.4. The conceptualized intelligent poultry feed dispensing system [17]

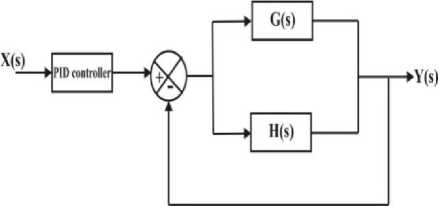
Fig.5. Closed loop representation of the poultry feed dispensing system [17]

• B.    Objective Function Formulation

To formulate an objective function for the tuning of the PID controller, it is expedient that consideration should be given to some performance indices based on the original transfer function of the system. The system will turn out optimum if it is capable of minimizing the performance index to a zero or positive value. The performance indices used for the system design are the Integral of Squared Error (ISE), Integral of Time Multiply Squared Error (ITSE), Integral of Absolute Error (IAE), and Integral of Time Multiply Absolute Error (ITAE).

The integral of the square error (ISE) helps to greatly minimize any negative and minimum outcome of the error value. Equation (4), gives the expression of the ISE.

/i = j” e2 (t^dt (4)

The integral of the Time Multiplied Squared Error (ITSE) gives results that are similar as combined with the same time weighting for Integral of Time Multiplied Absolute Error (ITAE). Equation (5), gives the expression for the ITAE.

/2 = /0” te2(t)dt                 (5)

The Integral of Absolute Error (IAE) is good for nonmonotonic step responses. It integrates the absolute error over time. Although it tends to produce a slower response, under damped system the results are tolerable. Also in the system response, there is no addition of weight. Equation (6) shows an expression of the IAE.

/ 3 = f ” \^e(t)\dt                  (6)

This criterion provides a similar result as the Integral of Absolute Error (IAE), but put less weight on the error e(t) for small time and more for large time. Thereby minimizing time multiplied time multiplied absolute error of the control system. Hence, it restricts any transient which involves long duration. Equation (7) shows the expression.

/ 4 = J ” \e(t)\dt                (7)

Considering the second order equation of the transfer function of (3), we can compare the close loop performance of the PID controller with the already mentioned performance criteria.

• C.    Tuning PID Controller Using Genetic Algorithm

Genetic Algorithm is a nature-inspired algorithm, which consists of the process of selection, mutation and crossover, to search for many local minimal thereby increasing the probability of finding the global minimal. The GA PID tuning is done using MATLAB based graphic user interface tool. Although this tool simplifies the tuning of the controller, six steps were employed for better results. The results obtained from the proportional, integral and derivative gains are used on the system transfer function of (3).

• 1.    Defining the Structure of the Controller: The simplest structure is defined as the Laplace transform of (3).

• 2.    Choose the Parameters to be Tuned: These are the three gains K_p , K_t , and K_d .

• 3.    The Encoding Scheme: There are two encoding schemes used. These are the binary encoding scheme and the real encoding scheme.

• 4.    The Fitness Function: The fitness functions considered are the Integral of Squared Error (ISE), Integral of Time Multiply Squared Error (ITSE), Integral of Absolute Error (IAE), and Integral of Time Multiply Absolute Error (ITAE). These were used because of their

• 5.    Structure of GA: Here simple GA and the elitism operator were used.

• 6.    The Parameters of GA: The Genetic Algorithm parameters used are Generation Count, Crossover Rate, Crossover Function, Mutation Function, Selection Function, and an Elite Count of 1.

G(s) = ^ = К_р + y+ K_d s

Where,

G (s) is the transfer function of the controller,

K_p is the proportional gain, K_t is the integral gain, and K_d is the derivative gain.

simplicity in implementation and wide range of application. These fitness functions are implemented in m-files. The m-file accepts the chromosome of the variables, decodes them, and extracts the gains K_p , K_t , and K_d .

• D.    Tuning of the PID Controller Using Particle Swarm Optimization

In PSO tuning of PID controller, the parameters of the controller (gains of the proportional, integral and derivative terms) and that of the algorithm are first declared. Here the performance index used is the Integral of Absolute error (IAE). This is because as used in GA-PID tuning, IAE gives the best value. The program that makes up the PSO-PID tuning consists of three files.

• E.    PSO Optimization of Fuzzy Logic Controller (FLC)

In the hybridization of Particle Swarm Optimization Algorithm with Fuzzy Logic, the first step taken was to design the FLC. The controller was saved with the Fuzzy Inference System (FIS) extension name (.fis). Although there are three parameters that can be optimized, this research work used PSO to optimize the input and output scaling factor of the FLC. Others are the membership function, and the rule-base. Fig. 6 depicts the model of the PSO being used to optimize the FLC.

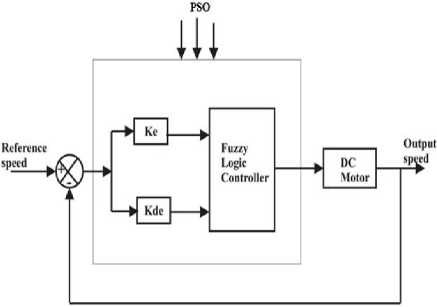
Fig.6. Structure of Fuzzy Logic Controller and Particle Swarm Optimization Algorithm

The main m-file used PSO in MATLAB. This work used two input scaling factors and the output scaling factor found in the Simulink file. The Lower bound and Upper bound on the search domain were respectively defined. The Simulink model displayed two scopes for both the input scaling factors and the output scaling factor.

• V. Results and Discussion

From the work carried out, different results were obtained after several simulations using GA and PSO. These repetitions were carried out to ascertain a better degree of the research results. Each process was carried out using different fitness function and different encoding scheme.

• A.    Results from Genetic Algorithm Tuning Of PID Controller

To obtain the best results, several simulations had to be carried out before any reasonable conclusion can be made on the authenticity of our result. Table 1 shows the results obtained using GA. Regardless of the type of fitness function used, Genetic Algorithm will find same solutions for the PID controller. From Fig. 7 and 8, it can also be observed that with a small population size, good results were obtained. Meaning that with smaller population size and initial condition, GA converges fast to the results.

From the results, it can be observed that with a small population size, good results were obtained. Meaning that with smaller population size and initial condition, GA converges fast to the results.

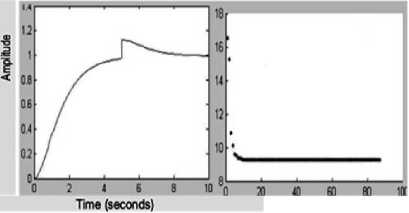
Fig.7. Simulation with population size of 10 using IAE

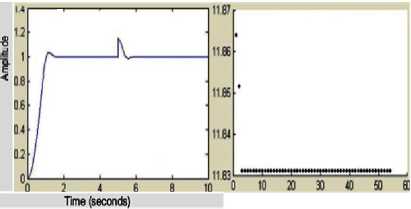
Fig.8. Simulation with population size of 100 using IAE

	Table 1. Simulation results for tuning the PID controller using GA
S/No	Performance Indices (Fitness function)                   PID Gains                          Response IAE        ITAE      ISE        ITSE       Kp        Ki         Kd        OS (%)     RT (sec)    ST (sec)
1	9.2353      15.0155     25.1209     20.5242     1.2372      -0.004      0.3429      0           2.6179      3.2621
2	3.3731      2.4155      11.8786     3.9527      21.5009     0.0057      4.04872    2.6417      0.66411     1.5146
3	3.453       2.9617      11.849      3.8919      46.673      0.2992      5.1222      5.722       0.6445      1.3939
4	3.255       2.0605       11.831      3.8363      49.801      0            7.3411      1.295       0.6456      1.0456
5	3.255       2.0615       11.830      3.8345      48.995      -0.006       7.0941      1.538       0.6515      1.0349
6	3.253       2.0529      11.830      3.8351      49.731      -0.003       7.2616      1.3895      0.6416      1.0423
7	13.195      45.539      30.898      56.662      1.2170      0.2313      0.5138      0           2.8689      4.3781
8	3.6211      4.2011      11.834      3.8678      39.312      -0.572      5.2482      3.4962      0.6305      1.3667
9	3.2566      2.0644      11.8325     3.8391      49.2972     0           7.44868     1.2956      0.64563     1.0433
10	3.2685      22.133      11.8309     3.8368      44.1292     0           5.60117     3.5597      0.63843     1.3312

• B.    Results from Particle Swarm Optimization Tuning of PID Controller

A summary of the results obtained is as shown in Table 2. This shows more desired value for the performance indices and responses. This is as a result of its parallel structure, fast convergence and the ability PSO possesses to prevent getting stuck in a local optimum solution.

Table 2. Simulation results for tuning PID controller using PSO

Performance Index	Gains			Response
IAE	Kp	Ki	Kd	OS (%)	RT (sec)	ST (sec)
2.0023	2.5253	0.0453	4.9213	3.8794	0.4232	10.324
2.0451	2.5455	0.0036	4.9543	3.4532	0.5342	5.8768
2.0454	2.4323	0.0038	4.8454	2.7658	0.6753	2.4511
2.1235	2.4322	0.0035	4.8341	2.2465	0.5891	2.4232
2.1022	2.4144	0.0034	4.8213	2.2443	0.5723	2.7682
2.1025	2.3543	0.0031	4.7875	2.1102	0.5643	2.4108
2.1043	2.3534	0.0029	4.7801	1.2859	0.5876	2.3241
2.1084	2.3823	0.0025	4.7732	1.2144	0.5545	2.2312
2.1067	2.3545	0.0026	4.7601	1.2011	0.4565	2.0211
2.1063	2.3312	0.0021	4.7221	1.0013	0.4179	2.0024

Fig. 9 shows an output of high percentage overshoot and some undesirable oscillation which later gets better with time as depicted in Fig. 10.

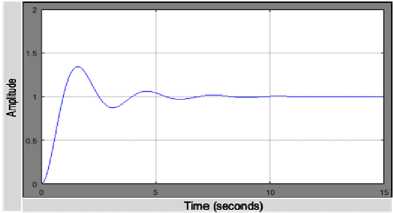
Fig.9. First control display of the PSO tuned PID controller

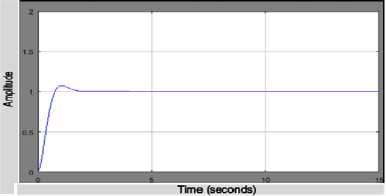
Fig.10. Final control display of the PSO tuned PID controller

From the simulation, while comparing the results of Table 1 and 2, it can be observed that PSO gave a better response than GA. This may be as a result of its parallel structure, fast convergence and the ability it possesses to prevent getting stuck in a local optimum solution.

• C.    Comparison of Results from GA-PID and PSO-PID

  Table 3 gives the comparison of the results obtained in the tuning of the PID controller. Given a much better percentage overshoot and rise time of 1.0013 and 0.4179 respectively, our focus was shifted to using PSO to tune the Fuzzy Logic Controller (FLC).

• D.    PSO Optimization of the Fuzzy Logic Controller

The displays of Fig. 11show the Best Function Values for the 30th iteration. The corresponding scopes display the step response for the input scaling gains and the output scaling gain respectively. Although our initial declaration was of 60 iterations, convergence was observed after 30 iterations. This shows the fast convergence possessed by PSO.

Any particle that creates the latest global best is the optimal solution of the Fuzzy Logic Controller. From Fig. 11a, it can be observed that after the 30th iteration, a better fitness value of 1.13214 was obtained as compared to the previous function value. After the fitness value had been determined, the optimization process was terminated, indicating convergence for an optimal value. Fig. 11b and 11c show the step response for the final input scaling gains and output scaling gain respectively.

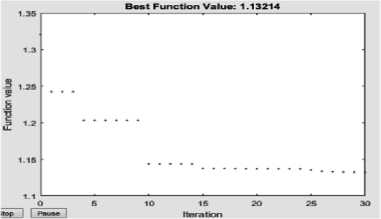
Fig.11a. Value of best function for the 30th iteration

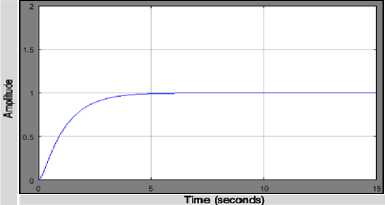
Fig.11b. Best global fitness plot

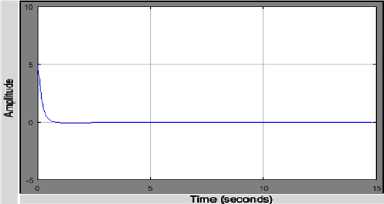
Fig.11c. Best generation fitness plot

Table 3. Result Comparison

Tuning Technique	IAE	Kp	Ki	Kd	Percentage Overshoot (%)	Rise Time (Sec)	Settling Time (Sec)
GA	3.2685	44.1292	0	5.60117	3.5597	0.63843	1.3312
PSO	2.1063	2.3312	0.0021	4.7221	1.0013	0.4179	2.0024

• VI. Conclusion

One of the challenges faced by engineers in the modeling of feedback control systems is the issue of stability. It is required that a system has the desired dynamic response characteristics for it to be considered stable. Therefore, it is necessary for an intelligent tuning of system controller to satisfy the necessary performance criteria of robustness, avoidance of excessive control action, and the minimization of the effect of disturbance. This channeled the research work towards the investigation of two nature-inspired optimization algorithms, GA and PSO, to PID controller. The dynamic system modeling is to help solve the problems of unusual human involvement, wastage of feeds, and contamination, to bring about a balance between cost of operation and feed cost thereby maximizing profit index. Although there are other nature-inspired algorithms, this work adopted GA and PSO because they are better suited in nonlinear system models. PSO algorithm was used in the optimization process for its efficient performance and faster convergence in the tuning of the inputs and output scaling factors of the Fuzzy logic controller. A much better system response and stability with the desired percentage overshoot, settling time and rise time were obtained.