Натурное моделирование пожара электрощита

В настоящее время большие данные являются одним из наиболее актуальных и перспективных направлений в мире информационных технологий. Современный мир ежедневно порождает огромное количество информации. В связи с этим возникает необходимость в использовании новых методов обработки и хранения больших данных. В статье рассматривается стохастическая блочная модель, которая выполняет разбиение на кластеры вершин случайного сгенерированного графа.

Актуальности исследования больших данных посвящено множество статей, следует формально определить, что же такое большие данные. Большие данные (Big Data) – группа технологий и методов обработки разноформатных данных большого размера, в распределенных информационных системах, для экономичного извлечения ценности, путем их быстрого захвата, обработки и анализа. При работе с данными такого объема традиционные инструменты не способны осуществить необходимые манипуляции за приемлемое время.

Необходимо определить какими характеристиками должны обладать данные, чтобы отнести их к категории больших данных [1]. Согласно последним исследованиям, большие данные имеют следующие параметры:

• 1)    Объем. Большими считаются данные, объем которых превышает сто терабайт.

• 2)    Скорость. Важна как скорость создания данных, так и скорость обработки.

• 3)    Разнообразие источников и форм хранения данных. Данные содержат неструктурированную информацию, необходима возможность одновременной обработки разных типов структур данных.

• 4)    Достоверность. Данные имеют внутреннюю ценность.

Следует отметить, что большие данные поступают непрекращающимся потоком, вследствие чего очень часто плохо структурированы, имеют большое количество пропусков и нуждаются в предварительной обработке. Одним из способов предварительной обработки данных выделяют кластерный анализ.

Кластерный анализ (кластеризация, cluster analysis) – это разбиение исследуемого множества объектов на группы «похожих» объектов, называемых кластерами [2]. В задаче кластеризации происходит отнесение объекта к одному из заранее неопределенных классов. Именно в этом состоит принципиальное отличие кластеризации от классификации. Решением задачи классификации является отнесение каждого из объектов к одному из заранее определенных классов. Разбиение объектов по кластерам осуществляется при одновременном формировании кластеров.

Кластерный анализ в общем виде состоит из следующих этапов:

• -    отбор данных (объектов) для анализа;

• -    определение множества переменных, по которым будет происходить оценивание объектов в выборке, при необходимости - нормализация значений переменных;

• -    выбор меры сходства (расстояния) между объектами;

• -    применение метода кластеризации;

• -    содержательная интерпретация кластеров, состоящая в изучении свойств объектов, попавших в каждый кластер;

Отдельно важно отметить роль содержательной интерпретации каждого класте- ра. Каждому кластеру необходимо присвоить содержательное название, отражающее суть объектов кластера. Для этого необходимо выявить, признаки, объединяющие объекты в кластер. Это может потребовать статистического анализа свойств объекта кластера [3].

Общепринятой и единой классификации методов кластеризации не существует, однако выделяют ряд методов, которые можно классифицировать по различным признакам [4]. На рисунке 1 представлен пример такой классификации.

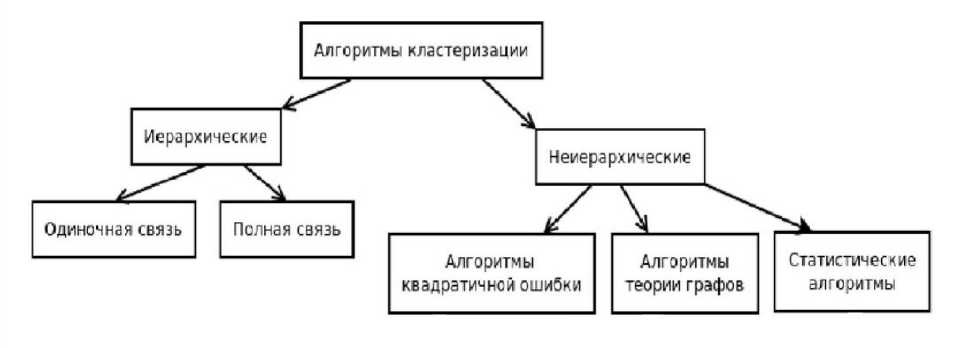
Рис. 1. Классификация методов кластеризации

Статистические методы кластеризации - группа методов, которые используют статистические модели для выявления кластеров [5]. Они используются для выделения групп объектов схожих между собой по некоторым признакам. Отдельное место занимают неиерархические алгоритмы, основанные на теории графов. Суть таких алгоритмов заключается в том, что выборка объектов представляется в виде графа, вершинам которого соответствуют объекты, а ребра имеют вес, равный «расстоянию» между объектами. Достоинством графовых алгоритмов кластеризации являются наглядность, относительная простота реализации и возможность внесения различных усовершенствований, основанных на геометрических соображениях.

Метод SBM. Стохастическая блочная модель (Stokhastic Block Model или SBM) - это статистический метод кластеризации для графов [6]. Он используется для выяв- ления структуры в графах и разделения вершин на группы (кластеры) на основе сходства между ними. В его основе лежит моделирование случайных графов. Особенностью метода является его вариативность в плане требований к восстановлению кластерной структуры, а именно слабое, сильное и точное восстановление. Помимо этого, преимуществом алгоритма является возможность проверки условий разделимости графа.

Пусть У - множество вершин графа размера п 6 N и к 6 N - предполагаемое количество кластеров, на которое разделяется множество вершин. Относительные размеры кластеров описываются с помощью вектора вероятностей р = (р1, .„,рк). Если pi имеет большое значение относительно остальных элементов р, то, вероятнее, соответствующий кластер велик относительно остальных. Пусть X - случайный вектор размерности п, который состоит из элементов, показывающих принадлеж- ность объектов к кластеру, вектор «лейблов». Компоненты этого вектора являются элементами из вектора к = {1, .^,к] c вероятностью р = (р1, ,„,рк). Вероятности связи вершин графа определяются с помощью симметричной матрицы W размера к X к, элементы которой распределены в [0,1]. Пара вершин (Vptj) EVxV, где i,j £ 1,...,п связаны ребром с вероятностью WX.Xj £ W.

Метод SBM получает на вход п, вектор р и матрицу W. Затем строит пару (X, G"), где G- неориентированный граф из п вершин, в котором вершины i и j соединены ребром с вероятностью W_x._Xj независимо от других пар вершин. На выходе образуются к кластеров размера пр 1 , .„,пр _к . Логика работы метода состоит в разделении вершин размеченного графа на кластеры, внутри которых находятся наиболее плотно связанные между собой вершины. Ребра, связывающие вершины графа, больше распространены внутри кластеров, чем между ними, так как наличие ребра между вершинами является признаком «связи» между ними. Целью обнаружения кластера является восстановление вектора разметки X с некоторым уровнем точности путем наблюдения G.

Как было сказано выше, стохастическая блочная модель позволяет по-разному восстанавливать кластерную структуру. Алгоритм обнаружения кластеров с точностью а £ [0,1] принимает на вход граф, полученный в результате работы метода SBM, на выходе - преобразование X ' (любое преобразование элементов вектора X фиксированной перестановки к) из X с уровнем точности α с вероятностью 1 — о_п(1). Выделяют следующие виды восстановления кластеров:

• 1)    Слабое восстановление. Алгоритм SBM восстановит кластерную структуру, если существует алгоритм с точностью а = 1 + г, г >  0.

• 2)    Сильное восстановление. Алгоритм SBM восстановит кластерную структуру, если существует алгоритм с точностью а = 1 — о_п(1).

• 3)    Точное восстановление. Алгоритм SBM восстановит кластерную структуру, если существует алгоритм с точностью а = 1.

Точное восстановление требует идеальной реконструкции кластеров, сильное – почти идеальной, а слабое – улучшить случайный равновероятностный выбор.

Общая цель всех алгоритмов обнаруже- ния состоит в определении наличия скрытой структуры в графе. При слабом восстановлении определяется скрытое разделение в смысле поиска раздела, который связан с истинным разделением гораздо лучше, чем случайное предположение. Другими словами, это означает, поиск скрытых группы в данных и определение их связи между собой. При точном восстановлении цель в том, чтобы точно восстановить скрытое разделение. Размеры кластеров и матрица вероятностей могут быть неизвестными. Здесь возникает вопрос как выбрать оптимальную точность а относительно параметров р и W.

Слабое восстановление является также простейшей моделью кластеризации на равновероятные и равные по размеру кластеры. Её называют Симметричной стохастической блочной моделью (Symmetric Stochastic Block Model, SSBM) [7]. В данной модели нет разницы между группами, вследствие этого вероятности между всеми кластерами равны, так же как и вероятности связи внутри кластеров. Вектор вероятностей имеет следующий вид: р = ( 1 , .„, 1 ). Очевидно, что ни у какого кластера нет предпочтения, поэтому их размеры одинаковы и равны П , где п £ N - число вершин графа, к £ N - количество кластеров. Пусть а - вероятность связи внутри блоков, b - вероятность связи между блоками. Матрица W имеет следующий вид:

( Cl b

b

b

b

b

b

b)

C/

Входными модель имеет следующие параметры - SSBM (n, p, c , b), выходными - матрица смежности W и метки кластеров для каждой вершины.

Метод SBM является новой технологией и находится в процессе развития, однако уже сейчас данная модель широко применяется в различных областях. Данная модель создает графы, содержащие сообщества, подмножества внутри себя, которые позволяют делать выводы об их структуре и связи с друг другом. В первую очередь, стохастическая блочная модель используется для анализа графов. Она позволяет разбить вершины графа на несколько блоков и определить, какие вершины находятся в одном блоке. Для использования модели необходимо задать число блоков и параметры распределения вершин. Затем можно оценить параметры модели по данным графа и использовать ее для обнаружения сообществ. Кроме того, модель может использоваться для анализа социальных сетей. Она выявляет похожие сообщества в популярных социальных сетях. В этом случае вершины графа пред- ставляют пользователей, а ребра между вершинами - связи между пользователями. Похожим образом, метод SBM работает в биоинформатике и биофизике. В биологии стохастические блочные модели используют графы для обнаружения групп генов, которые работают вместе в клетке, а в физике - для анализа структуры материи на микроскопическом уровне.

Результаты работы метода . Входными данными для метода является количество вершин графа и предполагаемое количество кластеров в нём. Для наглядной демонстрации работы алгоритма ниже будут представлены графы, разбитые на кластеры, с помощью стохастической блочной модели, с различным числом вершин и кластеров. Тестирование проходило в порядке увеличения вершин графа и количества кластеров. На рисунке 2 представлен неориентированный граф, состоящий из 22 вершин, построенный по случайно смоделированной матрице смежности. После использования алгоритма граф был размечен по цветам на 2 кластера.

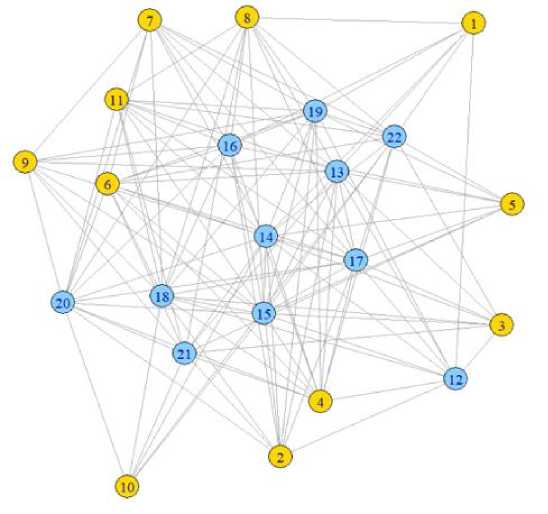
Рис. 2. Размеченный на 2 кластера граф из 22 вершин

Далее, число вершин графа выросло до 100. Матрица смежности вновь случайно смоделирована. Граф, по-прежнему, неориентированный, но значительно увели- чился в размерах, количество его ребер достигло почти 4000. Было задано разбиение на 5 кластеров. На рисунке 3 представлен полученный граф.

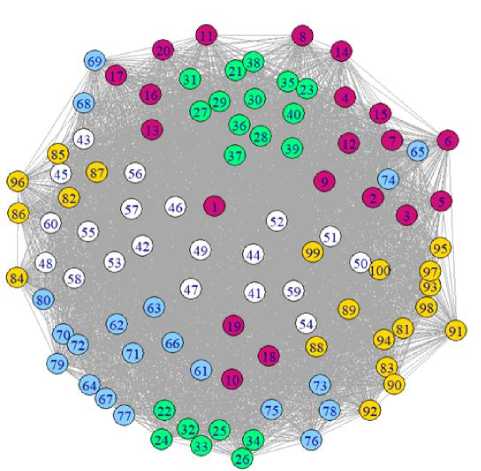
Рис. 3. Размеченный на 5 кластеров граф из 100 вершин

Финальным является граф из 1000 вершин, который также разбивается на 5 кластеров (рисунок 4).

о

Рис. 4. Размеченный на 5 кластеров граф из 1000 вершин

Заключение. Подводя итоги, можно сделать вывод, что алгоритм SBM представляет большой интерес благодаря своей эффективности и наглядной визуализации полученной кластерной структуры. В подтверждение этому в статье были освещены ключевые теоретические и практические аспекты стохастической блочной модели.

Метод находится на пике развития и имеет открытые проблемы, решение которых является перспективной работой. Например, одной из проблем является определение оптимального числа кластеров. В дальнейшем могут быть изучены различные варианты реализации и модификации алгоритма, а также способы минимизации вычислительной сложности без потери точности. Всё вышеперечисленное вновь говорит о востребованности и актуальности метода. Стохастическая блочная модель может быть использована для решения задач в различных областях, таких как экономика, информатика, социология и т.д. Изучение возможности применения метода SBM для решения задач в перечисленных областях является перспективным направлением дальнейших исследований.