Наведение и управление космическим роботом при визуальной инспекции состояния геостационарного спутника

Информационные спутники на геостационарной орбите (ГСО) имеют потребную длительность службы до 25 лет при наличии технического обслуживания с помощью космических роботов-манипуляторов (КРМ), в частности дозаправки топливом их электрореактивных двигательных установок. Предшествующая статья авторов [1] в этом же выпуске журнала содержит выбор отечественных реактивных двигательных установок (РДУ) для выведения КРМ по комбинированной схеме на ГСО и электромеханических приводов системы управления движением (СУД) КРМ для его сближения с целью (геостационарным спутником) от расстояния 500 м до дальности 100 м на интервале времени t e [1637,2185] с, синтезированные алгоритмы наведения и управления, а также результаты нелинейного анализа динамики СУД при таком сближении.

В данной статье рассматривается маневрирование КРМ в окрестности цели на расстоянии 80-120 м при визуальной инспекции её состояния с последовательным наблюдением из 6 точек в порядке возрастания их номеров с зависанием в каждой точке относительно цели на 5 минут, рис. 1 a .

ПОСТАНОВКА ЗАДАЧИ

Модели движения КРМ, состав СУД, ис- пользуемые алгоритмы наведения и управления детально представлены в [1], поэтому здесь приводятся только необходимая информация.

Применяется геоцентрическая инерциальная система координат (ИСК) I е с началом в цен тре Земли Оф {•} = col(-), 0t

и общепринятые обозначения и °,"~ для векторов, матриц и

кватернионов, а также матрицы [a] i элементарного поворота вокруг i -ой оси на угол a , i = 1,2,3 = 1 ^ 3. Используются Гринвичская система координат (ГСК) G@, связанная с Землей, орбитальные системы координат (ОСК)

O_r x ⁰ y ⁰ z ⁰ КРМ с началом в его полюсе O_r и цели O t x t⁰ y t⁰ z t ⁰ с началом в её полюсе O_t , а также связанная с корпусом КРМ система координат (ССК) O r xyz .

Предполагается, что на борту КРМ имеется наблюдательный инструмент (телескоп), ось визирования которого параллельна оси O _ry ССК робота, см. рис. 1. Как и в статье [1], приводами СУД являются: 1) РДУ на основе восьми реактив-

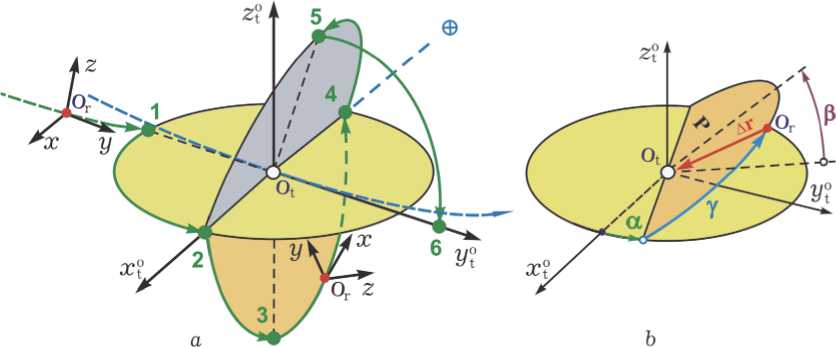
Рис. 1. Схема перелётов КРМ при визуальной инспекции состояния геостационарного спутника

ных двигателей по симметричной схеме при широтно-импульсной модуляции значений тяги 25 Н каждого двигателя с периодом T U = 4 с, что позволяет одновременно создавать векторы импульсов силы и момента произвольного направления в ССК робота; 2) силовой гироскопический кластер (СГК) на основе четырёх гиро-динов с собственным кинетическим моментом (КМ) h g = 100 Нмс и цифровым управлением с периодом T_u = 0.25 с.

Если считать КРМ твёрдым телом с массой m и тензором инерции J , то при стандартных обозначениях модель его пространственного движения в проекции на оси ССК O r xyz имеет вид r * + ® х r = v ; m ( v * + ю х v ) = P ^e + F ^d;

Л = Л о ю/2; J bo + ®x G = Mg + Me + Td.

Здесь кватернион Л = ( X₀ , X ) с вектором X = { X i } представляет ориентацию КРМ в ИСК; G = J to + H является вектором КМ механической системы, где H - вектор кинетического момента СГК; векторы P ^e , M ^e и M g = — H * представляют соответственно управляющие силы РДУ, моменты РДУ и СГК, векторы F ^d и T d

• - внешние возмущающие силы и моменты, а также используется символ ( • ) * локальной производной по времени. Применяемые дискретные алгоритмы широтно-импульсного и цифрового управления детально представлены в [1].

В статье решаются две задачи: 1) синтез алгоритмов наведения КРМ в процессе инспекционного облёта геостационарного спутника с последовательным наблюдением его состоя-

2185       2485          2885       31853585

|наблюдение 1| переход 1-2 I наблюдение 2] переход 2-3

300          400         300400

3585        3885          4285        45854925

I наблюдение 3 I переход 3-4 I наблюдение 41 переход 4-5

4985       5285           5685       5985

I наблюдение 5 I переход 5-6 I наблюдение 61

300          400           300

Рис. 2. Временная ди а грамма пе р елётов КР М и наблюдений состояния сп у тника

ния из 6 точек с заданных расстояний; 2) анализ динамики СУД робота с массой m ® 3000 кг при таком облёте.

ЗАКОНЫ НАВЕДЕНИЯ РОБОТА ПРИ ПОСЛЕДОВАТЕЛЬНОМ ОБЗОРЕ ЦЕЛИ

В ОСК цели перемещение КРМ между наблюдениями задаётся плоскостью P , положение которой назначается фиксированными углами а и р на рис. 1 b , и расположением полюса O r КРМ в этой плоскости, которое определяется углом у( t ) и модулем 5 ( t ) = A r ( t ) вектора s ( t ) = —A r ( t ) . рис. 1 b . Задача пространственного наведения КРМ состоит в программном расположении s p ⁽ t ) = ^{—A r p (} t ) полюса O _r КРМ в плоскости P ОСК цели и в программной ориентации оси O _ry по орту вектора A r p , когда ось O _rz ССК робота направлена по нормали к плоскости перемещения его полюса O _r .

Пусть номер j = 1 ^ 5 перелёта (перехода) между точками инспекции соответствует точке завершения предыдущего наблюдения, см. рис. 1 a. Временная диаграмма перелётов КРМ приведена на рис. 2, где переходы КРМ между точками наблюдения отмечены синим цветом, а участки наблюдения, где КРМ стабилизируется в ОСК цели, - зеленым цветом. В верхней части диаграммы указано текущее время, а в нижней части - длительности наблюдения.  Здесь длительность j -го перелёта принята одинаковой Tj = 400 с V j = 1 ^ 5, также как и длительность 300 с (5 минут) наблюдения геостационарного спутника из каждой точки, см. рис. 1 a и 2.

Таблица 1. Параметры перелётов КРМ

j	α j , град	β j , град	Y Р , град	Y p , град	s P , м	s P , м
1	0	0	- 90	0	100	100
2	0	- 90	0	90	100	100
3	0	- 90	90	180	100	100
4	0	70	180	90	100	80
5	90	90	70	0	80	120

Заданные кинематические параметры для имитации перелётов КРМ при последовательной визуальной инспекции состояния спутника на ГСО приведены в таб. 1.

При j -ом перелёте КРМ вектор его требуемого расположения s p (t) определяется углом Yj (t) в плоскости, заданной фиксированными углами aj и р j, и расстоянием sj (t) от цели. Угол Yj (t) изменяется от начального (initial) значения yjj = Y j (tij) до конечного (final) значения yP j = Yj (ti j + Tj), где Tj — длительность p j -го перелёта. При этом расстояние sj (t) изменяется от начального значения sij. = sj (tij) до конечного sp = sj (ti. + T.). На рис. 3 представлена пространственная программная траектория перелётов КРМ в ОСК цели, полученная в компьютерной среде MatLab.

Для каждого j -го перелёта столбец s ^p ( t ) координат центра масс КРМ с модулем s ^p ( t ) определяется в ОСК O _t x_t⁰yjz j цели с помощью ортогональной матрицы Q _y = WWW t )] ; . При заданных краевых условиях

.,Р ~р • мР -мР -П- ^р -уР -о-^Y i j , ^Y f j ^{; Y} i j = ^Y i j = 0 ^{; Y} f j = ^Y f j = 0;

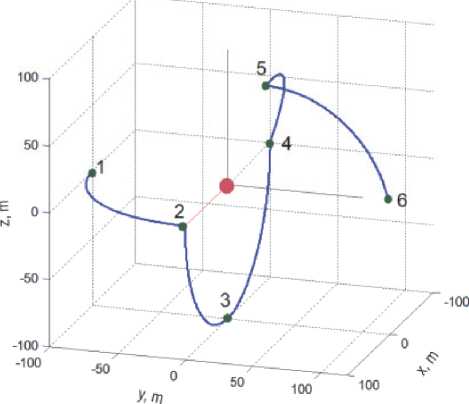
Рис. 3. Программная траектория перелётов КРМ движении, а также программных изменений кватерниона Лp, вектора модифицированных параметров Родрига с= {сi}, векторов угловой скорости top = {toj} и углового ускорения £p = {еj } робота.

Изменения вектора s ^p ( t ) = { s i ( t )} дальности полюса КРМ O _r от цели и его модуля s ^j ( t ) приведены на рис. 4. Здесь легко убедиться, что наблюдение геостационарного спутника из пятой точки выполняется при дальности 80 м, а наблюдение из шестой точки – с расстояния 120 м.

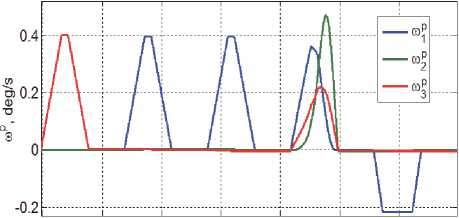
Рис. 5 представляет изменения вектора A v ^p = { A v j } программной скорости поступательного движения КРМ, где компоненты A v j этого вектора по оси O x ССК робота ( i = 1 ) отмечены синим цветом, по оси O ry ( i = 2 ) - зелёным и по оси O rz ( i = 3 ) - красным цветом. С применением такой же цветовой разметки на рис. 6 и 7 представлены изменения программных значений вектора модифицированных параметров Родрига ст = { с_t } и вектора угловой скорости to ^p = { to ^p } .

АНАЛИЗ ТОЧНОСТИ СУД РОБОТАПРИ ОБЗОРЕ СОСТОЯНИЯ СПУТНИКА

Как и в [1], при анализе точности поступательного перемещения КРМ используется вектор рассогласования 5 A r ^ { 5 A r } = A r ^p ( t ) — A r ( t ) между программной разностью A r ^p ( t ) и фактической разностью A r ( t ) расположений полюсов цели O _t и робота O r . При заданном в ИСК программном угловом движении КРМ (законе наведения) Л ^p ( t ), to ^p ( t ) погрешность ориентации КРМ определяется кватернионом E = ( e ₀ , e ) = Л ^p ° Л , вектором Эйлера E = {e ₀ , e } , где вектор

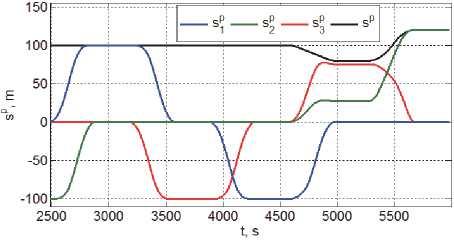
Рис. 4. Программная дальность КРМ от цели

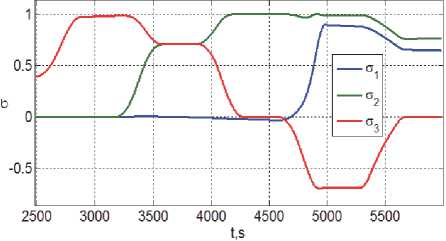
Рис. 6. Модифицированные параметры Родрига

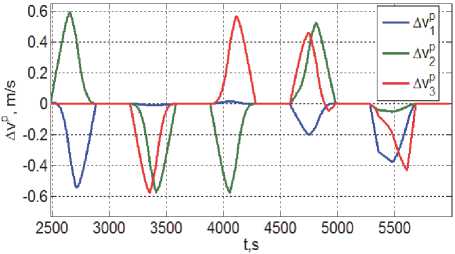
Рис. 5. Вектор программной линейной скорости

2500   3000   3500   4000   4500   5000   5500

t, s

Рис. 7. Вектор программной угловой скорости

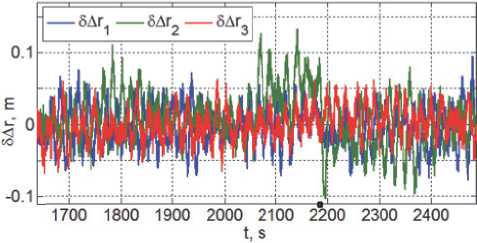
Рис. 8. Рассогласования в р асположе н ии КРМ

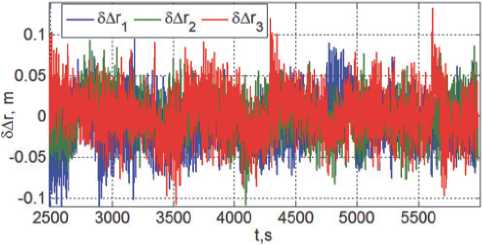
Рис. 10. Рассогласо в ания в расп о ложении КРМ

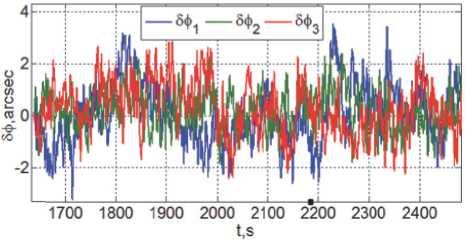
Рис. 9. Ошибки угловой с табилизац и и КРМ

Рис. 11. Вектор ск о рости пере м ещения КРМ

e = { e i } , матрицей С ^е( Е ) = 1 ₃ - 2[ e x ] Q ‘ , где Q e = I 3 e 0 + [ e x ] и вектором ошибки ориентации 5 ф = {5ф i } = { 2 e ₀ e i } , а погрешность стабилизации угловой скорости вычисляется по формуле 5 ® = { 5® i } = to — С ^е to p ( t ) .

На последующих рисунках кратко приводятся результаты нелинейного анализа точности системы управления движением КРМ, полученные методами компьютерной имитации.

На рис. 8 представлены рассогласования 5Аr в расположении КРМ сначала при сбли жении КРМ массой m = 3018 кг с геостационарным спутником с начальной дальности 500 м до расстояния 100 м на интервале времени t е [1637,2185] с длительностью 548 с, а затем в процессе наблюдения цели из первой точки в течение 300 секунд на интервале времени t е [2185,2485] с, см. временную диаграмму перелётов КРМ и наблюдений состояния спутника на рис. 2 и программную траекторию перелётов КРМ на рис. 3, а на рис. 9. приведены ошибки δφi угловой стабилизации КРМ на

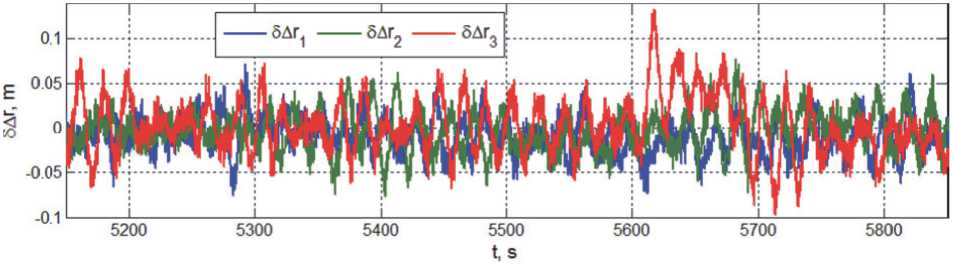
Рис. 12. Рассогласования в расположении КРМ при последнем перелёте и наблюдении

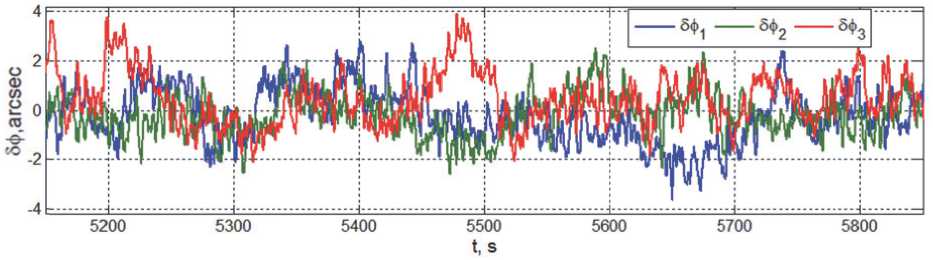
Рис. 13. Погрешности угловой стабилизации КРМ при последнем перелёте и наблюдении

интервале времени t е [1637,2485] с при выполнении тех же манёвров сближения и наблюдения. При этом момент времени t = 2185 с на рис. 8 и 9 отмечен точкой на оси абсцисс.

На рис. 10 и 11 представлены рассогласования в расположении КРМ и компоненты вектора A v = { A v i } фактической скорости его поступательного перемещения при перелётах КРМ и последовательном наблюдении состояния цели из точек 2 ^ 6 , см. также рис. 2 и 3.

Наконец, рис. 12 и 13 в удобном масштабе представляют рассогласования в расположении и погрешности угловой стабилизации КРМ при последнем перелёте и наблюдении состояния геостационарного спутника из шестой точки.

Из представленных результатов следует, что при наблюдениях состояния цели достигается точность не хуже 0.05 м по компонентам вектора расположения КРМ и не хуже 2 угл. сек по компонентам вектора погрешности его ориентации. Расчеты показывают, что на таких участках при частоте съемки 60 кадров/сек, фокусном расстоянии объектива 0.3 м и размере пикселя 9 мкм, изображение будет четким: смаз изображения составит не более 0.023 пикселя в любой точке кадра.

ЗАКЛЮЧЕНИЕ

Представлены разработанные алгоритмы наведения космического робота для облёта геостационарного спутника с последовательным наблюдением его состояния из 6 точек с задан- ного расстояния. В рамках принятого уровня моделирования КРМ выполнен анализ динамики системы управления движением робота при таком облёте, приведены численные результаты, демонстрирующие эффективность разработанных алгоритмов наведения и управления.

Отметим, что в алгоритмах широтно-импульсного управления реактивной двигательной установкой и цифрового управления силовом гироскопическим кластером применяются только позиционные векторные рассогласования, информация о рассогласованиях в скоростях поступательного и вращательного движений робота и геостационарного спутника не используется, этот факт значительно упрощает бортовую реализацию измерительных средств системы управления движением робота. Отмеченные алгоритмы подробно представлены в работах [2, 3].