Наведение и управление свободнолетающим роботом при завершении сближения с пассивным объектом в дальнем космосе

Разработка методов управления движением космических роботов-манипуляторов (КРМ), рис. 1, для механического захвата, транспортировки и сервисного обслуживания орбитальных пассивных космических объектов (ПКО) в условиях неопределенности и неполноты измерения состояния является актуальной научной проблемой. Решение данной проблемы позволит на регулярной основе продлевать сроки активного существования информационных спутников с уникальными техническими характеристиками и при необходимости перемещать такие спутники для технологической модернизации на борту орбитальной станции либо в наземных условиях. Здесь выделяются три ключевые задачи: 1) разработка бесконтактных методов идентификации кинематических параметров движения ПКО с помощью оптико-электронных камер и лазерных дальномеров КРМ; 2) разработка методов наведения и управления пространственным движением КРМ при завершении его сближения с ПКО; 3) подготовка к механическому захвату и исследование нелинейной динамики механического сцепления ПКО с КРМ. В обзорных статьях [1, 2] авторы провели анализ 55 научных работ и выделили проблемы теории систем управления движением свободнолетающих КМР. В статье [3] выполнен аналитический обор современных методов и технологий, связанных с кинематикой, динамикой, управлением и анализом воз можностей КРМ для пилотируемых и беспи-

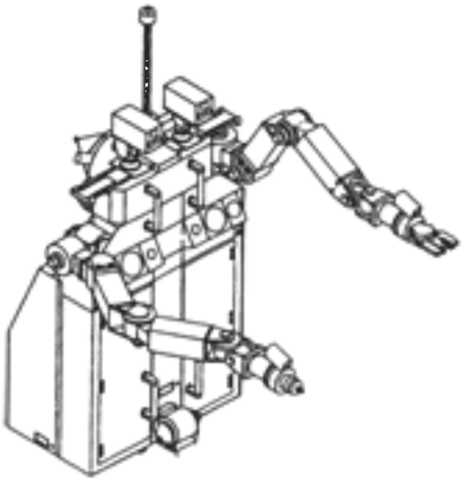
Рис. 1. Космический робот-манипулятор лотных орбитальных миссий обслуживания. В этой статье выполнен анализ 370 публикаций по указанной тематике и кратко представлен предложенный в монографии [4] многоэтапный процесс захвата и транспортировки цели (target).

При орбитальном движении ПКО в околоземном пространстве весьма непросто решение первых двух из указанных выше ключевых задач. Здесь идентификация кинематических параметров движения ПКО выполняется на основе информации, накопленной при последовательных наблюдениях за его движением с помощью бортовых оптико-электронных средств КРМ с различными ракурсами, и с учетом законов механики космического полета твердого тела в гравитационном поле Земли, Луны и Солнца, а также влияния сил солнечного давления, определяется положение центра масс ПКО, оценива- ются изменения углового положения и векторов скорости его поступательного и вращательного движений. Полученная в результате информация используется при синтезе закона наведения и формировании управления пространственным движением КРМ при завершении его сближения с целью. Целью данной статьи является разработка стратегии наведения и управления КРМ, а также оценка потребных ресурсов исполнительных органов его системы управления. Поэтому здесь рассматриваются первоочередные задачи наведения и управления движением КРМ при завершении его сближения с вращающимся ПКО в дальнем космосе, когда можно пренебречь внешними возмущениями, которые влияют на пространственные движения ПКО и КРМ. При этом регулярно используются инерциальная система координат (ИСК) и система координат, связанная с корпусом КРМ, которую обычно называют связанной системой координат (ССК), а также стандартные обозначения col(-) = {•}, HneQ = [•], (.)t, [ax] и о,~ для векторов, матриц и кватернионов.

ПРИВОДЫ СИСТЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ КРМ

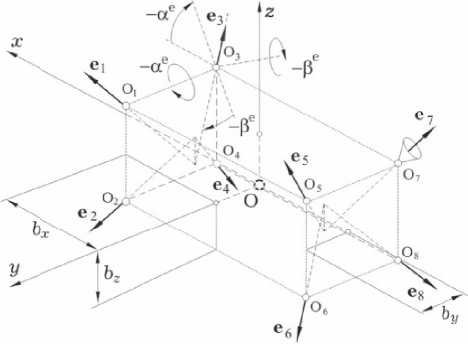
Рис. 2. Схема ДУ на основе 8 РД

p7 =

bx

^— b y b z

’ ^р 8

^^^^^^^в

b

^^^^^^^в

x

b y

^^^^^^^в

b z

Пусть каждый РД имеет широтно-импульсную модуляцию (ШИМ) тяги, что описывается нелинейными непрерывно-дискретными соот-

Предполагается совпадение положений центра масс КРМ и полюса O в ССК O xyz . На рис. 2 представлена симметричная схема двигательной установки (ДУ) на основе 8 реактивных двигателей (РД). Орты e p , p = 1,...8 = 1 g 8 , осей сопел РД имеют в ССК представления в виде

ношениями P p ⁽ t ⁾ = ^pm PWM( t-T ^ .t , T ,v _p , ) V t e [ t_r , t_{r + 1}) с периодом T и временным запаздыванием T u . Здесь v _pr является входным сигналом и функции

PWM( t,t_r, T m ,v pr ) ^

' signv pr 0

t ^{e [} t r t r ^{+ T} pr ) _; t ^{e [} t r ^{+ T} pr , t r +1 )’

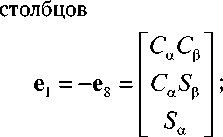
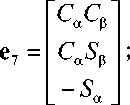
T (^ ) = pr m

. sat(T U ,|v p

I)

^|v pr ¹ <  ^T m

^|v pr ¹ >  ^T m ’

e з

— e

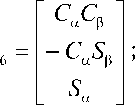
e 4

,

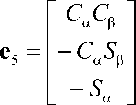
где 5x = sinx, Cx = cosx, x = ae, Pe. Векторы

Р p , P = 1 + 8 , точек O _p ра тяги РД в ССК (см. рис. 2) представляются

приложения векто-

столбцами

bx

bx

bx

Р1 =

b y

’ ^p 2 =

b y

’ ^p 3 =

b y

tr = rT tr+1 = tr + T. r e No ^ [0,1,2,3...), ,                                       ;

P m

- номинальное значение тяги, одинаковое для всех РД. В ССК вектор тяги p -го РД вычисляется по формуле p _p ( t ) = — p_p ( t ) e _p , а векторы силы P ^e и момента M ^e ДУ - по соотношениям P ^e = S p _p ( t ) = P = { P_v P ₂, Д} и M ^e = S [ p p x ] p _p ( t ) . Орты r _p векторов p _p вычисляются как r _p =p _p /р, где скаляр p = ( b x + b y + b ²) ^1/2 является единым модулем точек O _p приложения векторов тяги РД в ССК. При обозначениях

p(t) = РЧt)/Pm; m(t) = Me(t)/(Pmp}; тr = {тpr};

De = {[ep],[rp xep]}, tp = {pp,mp},

;

Р4 =

bz

b x

^^^^^^^B

b y

^^^^^^^^

b z

bz

bz

bx

bx

’ ^p 5 =

b y

bz

; Рб =

b y

bz

;

где векторы p ^p и m ^p представляют импульсы нормированных векторов сил p ( t ) и моментов m( t ) ДУ, заданные в ССК, принципиальная проблема заключается в решении векторного уравнения D ^e т _r = t r ’, т _r e R 8 , t r ¹ e R ⁶ при условии 0 < т _pr <  T U V p = 1 ^ 8 относительно

компонентов вектора-столбца т r = { т pr } , когда прямоугольная матрица D ^e и вектор-столбец t p е R ⁶ заданы. При использовании псевдо-обратной матрицы ( D ^e) # ^ ( D ^e)^t( D ^e( D ^e)^t) ^{- 1} закон распределения длительностей т _pr тяги всех 8 РД на полуинтервале времени t е [ t r , t r _{+ 1}) с ШИМ их тяги с периодом T U имеет простую алгоритмическую форму

— r ^ : — pr} = (De)# tpg; тpr =: т pr - min (т pr), (1) if q = max (Tpr) > TU then Tpr = тpr-T,eTpr i q, а векторы тяги Pe и момента Me определяются формулами Pe(t) = Pmp(t) и Me(t) = Pmp m(t).

При цифровом управлении ДУ каждый РД имеет кусочно-постоянное значение тяги p p ( t ) е [0,P ^m ] V t е [ t r , t r _{+ 1}) с постоянным периодом T и временным запаздыванием T Zu , где P ^m >  0 - максимальное значение тяги, одинаковое для всех РД. При отсутствии квантования по уровню формирование такого цифрового управления описывается соотношением P p ⁽ t ⁾ = Zh⁽ t -TA , TA_pr ⁾ V t e [ t_r , t_r J, где функция y r ( t ) = Zh( t,t r , A X r ) = X r V t e [ t r , t r ₊J описывает процесс фиксации сигнала x_r на полуинтервале [ t r , t r _{+ 1}) . Здесь при обозначениях p r = { p_pr } - вектор-столбец, составленный из значений тяги всех 8 РД; t e = { P r e , м e } – столбец, составленный из заданных в ССК векторов силы P r и момента M r ДУ; D ^e = {[ e _p ],[ p _p x e _p ]} – прямоугольная матрица, проблема заключается в решении уравнения D ^e p r = t r , p r е R 8 , t r е R ⁶ при условии 0 <  p_pr <  P ^m V p = 1 ^ 8 относительно компонентов вектора-столбца p r = { p_pr } . В этом варианте закон распределения цифровых значений тяги всех 8 РД на каждом полуинтервале времени t е [ t r , t r _{+ 1}) с периодом T U имеет такую алгоритмическую форму:

..                                                       .                                                                                                                                                                                                        ..                                                                                                                .

Р г = { P pr } = (D^e) # t r ; P pr =: P pr - min ( p_p r ), (2) if q = ^{max (}P pr ⁾ > P^m then p pr = pp, ^/ q •

Последняя строка в алгоритме (2) явно указывает на ограниченность управляющих векторов силы P ^e и момента M ^e двигательной установки, постоянных на полуинтервале времени t ^{е [} t r , t r +1 ) .

Для управления ориентацией КРМ применяется силовой гироскопический кластер (СГК) четырех гиродинов (ГД). На рис. 3 представлена каноническая схема 2-SPE (система 2 ножничных пар – 2 Scissored Pair Ensemble), состоящая из двух пар ГД с ортами кинетических моментов (КМ) hp (вp ), p = 1 ^ 4, область вариации нормированного вектора КМ такого кластера h(P) = Shp(вp), где столбец P = {Pp}, и ее проекции на плоскости симметрии гироскопического базиса Oxgygzg.

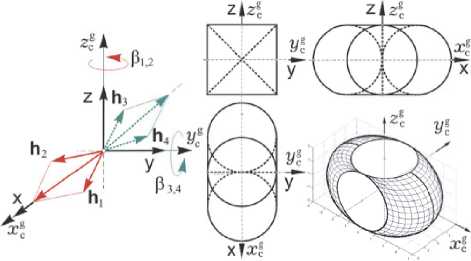
Рис. 3. Схема СГК и область вариации его КМ

Все внутренние сингулярные состояния схемы 2-SPE являются проходимыми [5], применяемый [6] явный аналитический закон настройки СГК (распределения трехмерного вектора его управляющего момента M ^g между четырьмя ГД) позволяет исключить избыточность данного кластера с вектором кинетического момента H = h g h ( P ) , где h _g - одинаковое для всех четырех ГД постоянное значение модуля собственного КМ. При цифровом управлении “ I ⁽ t ⁾ = ^{^ рк ⁽ t ^{)} с} периодом T , где ^u^⁽ t ⁾ = ^u^ V t е [ t_k , t_k + 1 ) , t_k + 1 = t_k + T и k е N o , СГК формирует управляющий момент ■

M g ( t ) = - h g A h ( P ( t ) u g ( t ) ; P ( t ) = u k ( t ) , (3) где прямоугольная матрица A h ( P ) = d h ( P ) /3P .

МОДЕЛИ ДВИЖЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Пусть в ССК, вращающейся относительно ИСК c вектором угловой скорости to (t) ^ {to i(t)} , i = 1 ^3, задан вектор a(t) = {ai(t)}. В ИСК этот вектор отображается в виде а'(t) = {ai(t)}. Угловое положение ССК относительно ИСК определяется кватернионом Л = <Хо,Х) , X = {XJ , который изменяется согласно кинематическому уравнению Л = Л ° ю/2 . Далее применяется также вектор модифицированных параметров Родрига (МПР) О = {оi} = e 1!(Ф / 4) с обозначениями орта Эйлера e и угла Ф собственного поворота. Вектор о взаимно-однозначно связан с кватернионом Л прямыми О = X/ (1+ Х0) и обратными X 0 = (1 -О 2)/(1 + О2), Х = 2о /(1 + о2) соотношениями. Отображения вектора a(t) в ССК и a'(t) в ИСК связаны соотношениями a(t) = Л(t) ° a'(t) ° Л(t) и a' (t) = Л(t) ° a(t) ° Л(t), а производные по вре- мени этих отображений – классической формулой Эйлера a I (t) = d a I / dt = a* (t) + to(t) x a(t) для дифференцирования вектора в подвижной системе координат, где a*(t) = d a / d t является локальной производной вектора a(t) по времени в ССК.

Будем считать, что КРМ массой m оснащён двигательной установкой на основе 8 РД, которая создает только вектор силы P = { P_t } , и СГК на основе 4 ГД с вектором управляющего момента M ^g = {M^g} . Предполагая отсутствие всех внешних возмущений в дальнем космосе, модель пространственного движения КРМ при отображении на оси ССК принимается в виде

Г , * + tox r r = V r ; v , + to x v r = w ,    (4)

Л = Л о ю/2 ;    J to । ШХ G ⁰ = M ^g . (5)

Здесь уравнения (4) с векторами положения r _r и скорости v _r описывают поступательное движение КРМ ( robot , нижний индекс r ), где вектор w = {w i } = P /m является управляющим ускорением, а уравнения (5) представляют управляемое вращательное движение КРМ с тензором инерции J , где G ⁰ = J to + H является вектором кинетического момента системы твердых тел.

Будет для простоты считать, что в ИСК поступательное движение ПКО с векторами положения r t ¹ и скорости v | ( target , нижний индекс t ) является прямолинейным и равномерным, а его вращательное движение происходит вокруг фиксированного в ИСК орта e _t ^ω вектора угловой скорости. В ССК векторы дальности Δ r до цели и рассогласования Δ v между скоростями КРМ и ПКО вычисляются по соотношениям Δ r = r _t - r _r и Δ v = v _t - v _r соответственно.

Завершение сближения КРМ с ПКО начинается при дальности Ari ~ 500 м, когда КРМ располагается внутри конуса с началом в центре масс ПКО, осью симметрии по отрицательному направлению орта скорости vt цели и углом полу-раствора 60 град. Задача состоит в синтезе законов пространственного наведения и управления движением КРМ, при которых робот за заданное время сближается с целью до дальности Arf « 30 м, когда орт ex его бортовой видеока-ω меры становится параллельным орту et вектора угловой скорости ПКО, и стабилизации такого положения КРМ относительно подвижной цели с точностью ® 0.3 м. Последующие действия робота-манипулятора (разведение телескопических «рук», финальное сближение с ПКО при одновременной «закрутке» относительно орта ex для синхронизации вращений корпуса КРМ и цели, зависание с вращением и др.) связаны с третьей ключевой задачей захвата ПКО и здесь не рассматриваются.

ЗАКОНЫ НАВЕДЕНИЯ

В ИСК модель (4) поступательного движения КРМ принимает простой классический вид r,= v,; V, = w1,              (6)

где вектор ускорения w ¹ = w ’ ( t ) = Л ( t ) о w о Л ( t ) представлен в ИСК с помощью кватерниона Л ( t ) . При отсутствии вращения ( to = 0 ) ориентация КРМ в ИСК определяется постоянным кватернионом Λ _∗ , модели движения (4) и (6) совпадают и вектор ускорения w ¹ = Л , о w о Л , определяется в ССК, которая имеет фиксированное угловое положение в исходной ИСК, и, следовательно, по существу является локальной ИСК, развернутой относительно исходной.

С целью упрощения реализации требуемого вектора ускорения w с помощью ДУ в ССК принимается следующая стратегия построения законов наведения КРМ, состоящая из трех этапов: 1) разгон робота с постоянным вектором линейного ускорения w в ССК при фиксированной ориентации КРМ в исходной ИСК в процессе его поступательного движения; 2) прямолинейное равномерное движение центра масс КРМ с одновременным разворотом его корпуса для ориентации орта e _x бортовой видеокамеры в ИСК параллельно известному орту e _t ^ω вектора угловой скорости ПКО; 3) поступательное движение центра масс КРМ в локальной ИСК по траектории векторного сплайна соответствующего порядка с точным выполнением заданных краевых условий.

Синтез закона пространственного углового наведения КРМ (поворотного маневра) на некотором интервале времени t е [ t i ^p , t p ] с заданными краевыми условиями

Л( 1 ₁ ^p ) = Л _ ; to( 1 ₁ ^p ) = to _ ; e( t p ) = e _ ;               (7)

Л(tf) = Лf; to(tf) = tof; e(tf) = ef; e(tf) = ef выполняется при ограничениях на модули векторов его угловой скорости to (t), углового ускорения £ (t) и производной £ (t) по времени. При балансе системы управления КРМ по вектору КМ G0 с условием G0 = 0 модель динамики его углового движения принимает вид to = £ с вектором углового ускорения £ = J-1Mg, а модель углового движения (5) – кинематическое представление тЛ = Л о to /2; (О = £; £ = £*= v.       (8)

Разработанный закон углового наведения КРМ основывается на необходимом и достаточном условии разрешимости классической задачи Дарбу. Здесь решение представляется как результат сложения трех одновременно происходящих элементарных поворотов «вло- женных» базисов Ek вокруг ортов ek, k = 1 ^ 3 осей Эйлера, положение которых определяется по краевым условиям (7) модели (8). При этом искомый кватернион Л(t) определяется произведением Л (t) = Л i о Л1( t) о Л 2( t) о Л з( t), где Лk (t) = (cos(фk (t)/2), ek sin(фk (tУ2)), Функция фk (t) определяет угол k -го поворота, k = 1 ^ 3. В силу неподвижности орта ek в базисе Ek-1 имеем соотношения to k(t) = фk (t)ek , 6k(t) = фk(t)ek, 6*k (t) = 6k (t) =фk (t)ek. Введем обозначения to(k\ £(k), £(k), k = 1 ^ 3 векторов to, £ и £ в базисе Ek, оператор aw = ф(аk-i,Лk ) = Лk о ak-i о Лk преобразования вектора ak-1 из базиса Ek-1 в базис Ek и назначим to 1(t) = ф 1(t)е 1, £ 1(t) = ф 1(t)е 1 и £ 1(t) = ф1(t)е 1. Векторы to, £ и £*=£ в ССК определяются значениями этих же векторов в базисе E3, которые формируются по рекуррентным формулам, k = 2,3 :

to(k) =ФГю Л V £(k) = Ф(£ Л V tok-1 Ф(tok—1,лk ^ьk—1 ф(£k—1,Лk),

£k = ф(£k_1, Лk); to(k) = to + tok;

^{( k )} — р^{( k )               ( k )             ( k} ) _ р^{( k} ) I р I

£ = £k-1 + £к + tok-1 X tok ; £ = £k-1 + £k +

+ to(^ X £t + ^ + to(^ Xtok)Xtok .

k 1 k          k 1        k 1 k        k

.

В результате при назначении набора скалярных сплайнов ф _k ( t ) по явным аналитическим соотношениям получаются векторные функции to ( t ) = to ⁽³⁾ ( t ) , £ ( t ) = £ ⁽³⁾ ( t ) и £ * ( t ) = £ ( t ) = £ ⁽³⁾ ( t ) .

Пусть кватернион Л * = ( 1 0 , X * ) = Л i о Л _f имеет орт оси Эйлера e ₃ = X * / sin( ф * /2) третьего поворота, где угол ф * = 2arccos( X 0 ) . Для 1-го и 2-го поворотов позиционные краевые условия принимаются в виде Л 1 ( t ip ) = Л 1 ( t f ) = 1 , Л 2 ( t i p ) = Л 2 ( t f ) = 1 , а для 3-го поворота назначаются как

Лз(tip) = 1, Лз(tfp) = (cos(фf/2),e3 sin(ф3/2)), где ф!, = ф* и 1 - единичный кватернион. Орт e 1 оси Эйлера 1-го поворота назначается из условия его ортогональности орту e3, а орт e2 = e3 х e1. Векторы to (t), е(t), 6* (t) = 6(t) представляются в аналитическом виде при задании сплайнов ф k(t) различных порядков с использованием в общем случае трех участков заданного интервала ПМ [7]: 1) участок разгона с оптимизацией по быстродействию при ограничениях, где КРМ из заданных краевых условий на левом конце траектории переводится на движение с постоянным вектором угловой скорости по орту e3; 2) участок движения с указанным вектором угловой скорости по орту e3; 3) завершающий участок движения КРМ с гарантированным выполнением заданных краевых условий на правом конце траектории при использовании сплайнов 6-го порядка и соотношений (9). При этом все параметры скалярных сплайнов ф k (t) вычисляются по явным аналитическим соотношениям.

ЗАКОНЫ УПРАВЛЕНИЯ

Пусть задан закон углового наведения КРМ Л ^p ( t ), to p ( t ), (b p ( t ) = £ p ( t ) в ИСК. Кватерниону E = ( e ₀, е ) = Л p ° Л с вектором e = { e i } соответствует вектор параметров Эйлера E = ^{{ e} o , ^{e }} и матрица угловой погрешности C ^e = I ₃ - 2[ e x ] Q e , где Q _e = 1 ₃ e ₀ + [ e x ] . После дискретной фильтрации измеренных с периодом T_q значений вектора углового рассогласования 6 l =- 2 e ₀ l e l , l e N _o , формируются значения вектора 6 k , k e N _o , цифрового закона управления СГК с периодом T_u :

gk+1 = Bgk + C£k; mk = Kgk + P£k;

Mk = tok X G: + J(Ck £ p + [Cktop X]to k + mk).

Здесь Ср = Ce(E), G0 = J to   H и ис- k     k k   kk пользуются диагональные матрицы K, B, С и P. Далее вектор Mg с помощью явного закона распределения команд между 4 ГД «пересчитывается» в столбец uk = {ugp } сигналов управления ГД, которые фиксируются на полуинтервалах цифрового управления СГК с периодом Tu для формирования его управляющего момента Mk (t) (3).

При законе наведения A r ^p ( t ), A v ^p ( t ), w ^p ( t ) в поступательном движении КРМ выполняется фильтрации измеренных с периодом T_p значений вектора позиционного рассогласования 6 _s = ( A r S - A r _s ) , s e N _o , и с периодом T U формируются значения вектора 6 ^f , r e N _o , которые применяются в законе управления вектором P тяги двигательной установки

gk+1 = Bg k + C£ I;w k = Kg k+P£ k;

Pk = {Р»} ^ Pk = m(wp + w k).

Далее вектор P _k тяги ДУ распределяется между 8 реактивными двигателями по соотношениям (1) либо (2) при их широтно-импульсном или цифровом управлении с периодом T U соответственно.

РЕЗУЛЬТАТЫ ИМИТАЦИИ

При компьютерной имитации рассматривался космический робот-манипулятор с массой m = 1000 кг и тензором инерции J = diag{812; 587; 910} кг м². Было принято,

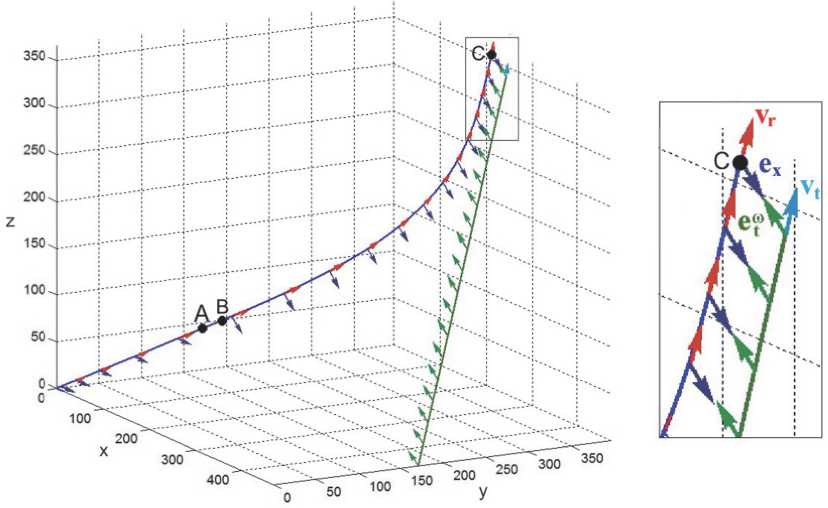
Рис. 4. Сцена пространственного сближения КРМ (синий цвет) с ПКО (зеленый цвет)

что при управлении с периодом T = 4 с каждый из 8 РД в составе ДУ имеет максимальное значение тяги Pm = 0.5 Н, расположение РД в ССК определяется плечами b = 1 м, b = 0.7 м, xy bz = 0.6 м и углами их установки ae = 35.25 град и вe = 45 град, см. рис. 2. При этом максимальная тяга ДУ по каждой из осей ССК одинакова и составляет 1.15 Н. Каждый из 4 ГД в составе СГК (см. рис. 3) имеет модуль собственного КМ hg = 30 Нмс и период цифрового управления Tu = 0.25 с. Пусть в момент времени t = ti = 0 КРМ неподвижен в ИСК (rr (ti) = 0, vr (ti) = 0) и его ССК совпадает с ИСК (Л(ti) = 1, to (ti) = 0 ), орт направления на цель c(ti) = {Cф, Sф ,0} при ф = 20 град и начальная дальность до цели Ar(ti) = Ari = 500 м, рис. 4. Поступательное движение цели в ИСК происходит с постоянным вектором скорости vt = {-0.05, 0.05, 0.075} м/с и ПКО вращается в ИСК вокруг орта e^= {-0.608, - 0.228, 0.760} . В момент времени t = tf = 4250 с («1.2 ч) требуется обеспечить сближение КРМ с целью при заданной дальности Ar(tf) = Arf = 30 м и параллельности орта ex орту eto, а также последующую стабилизацию такого положения КРМ относительно ПКО с точностью « 0.1 м. В соответствии с описанной стратегией выполнен синтез закона наведения КРМ с 3 этапами:

• 1)    при t е [0,1420) с производится разгон робота с постоянным вектором ускорения ^w в ССК, в результате достигаемая им позиция представлена точкой A на рис. 4;

• 2)    при t е [1420,1520) с КРМ совершает

равномерное прямолинейное движение с одновременным разворотом его корпуса для ориентации орта e x параллельно орту e to , достигаемая им позиция представлена точкой B на рис. 4, а закон углового наведения - на рис. 5, где 8 = 8 p ( t ) , to = to p ( t ) и G = Q p ( t ) ;

• 3)    при t е [1520,4250) с КРМ выполняет поступательное движение по траектории векторного сплайна шестого порядка с точным выполнением краевых условий A r( t _f) = 30 м, A v( t _f) = 0 и w( t _f) = 0 в точке C на рис. 4.

Закон наведения КРМ в поступательном движении с разворотом ССК представлен на рис. 6, где A r = A r p ( t ) , A v = A v p ( t ) , w = w p ( t ) .

На интервале времени t е [4250,5000] с дополнительно предъявляется требование стабилизации положения КРМ относительно ПКО с точностью ® 0.3 м. Отметим, что на рис. 5 и рис. 6 черным цветом отмечены модули соответствующих векторных функций.

Будем считать, что измерение ориентации КРМ выполняется астроинерциальной системой определения углового положения (СОУП), погрешности выходных дискретных сигналов СОУП с периодом T q = 0.125 с содержат центрированный гауссовский шум со среднеквадратичным отклонением (СКО) a a = 1 угл. сек и после дискретной фильтрации измеренных значений вектора углового рассогласования формируются значения вектора 8\ в цифровом законе управления СГК (10) с периодом T_u = 0.25 с. Как показано в [8 -10], для синтезированного закона углового наведения космического аппарата с инерционными параметрами, соответствующими КРМ, достигается точность ста-

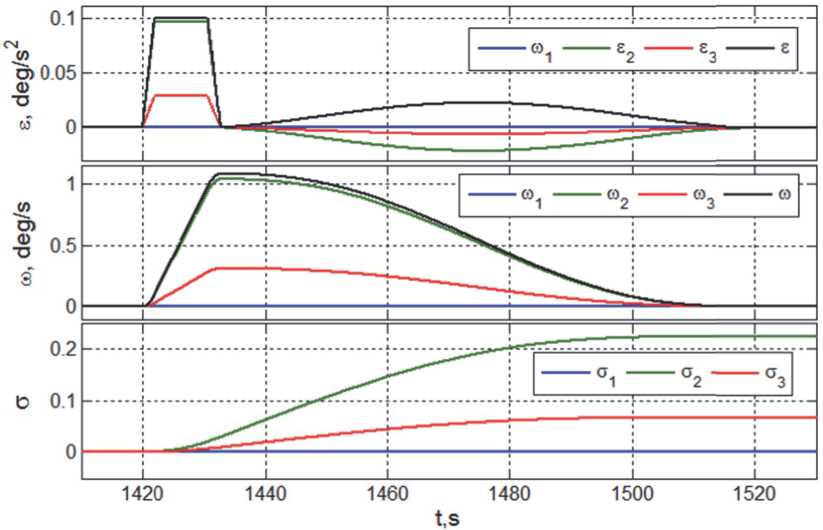
Рис. 5. Закон углового наведения КРМ

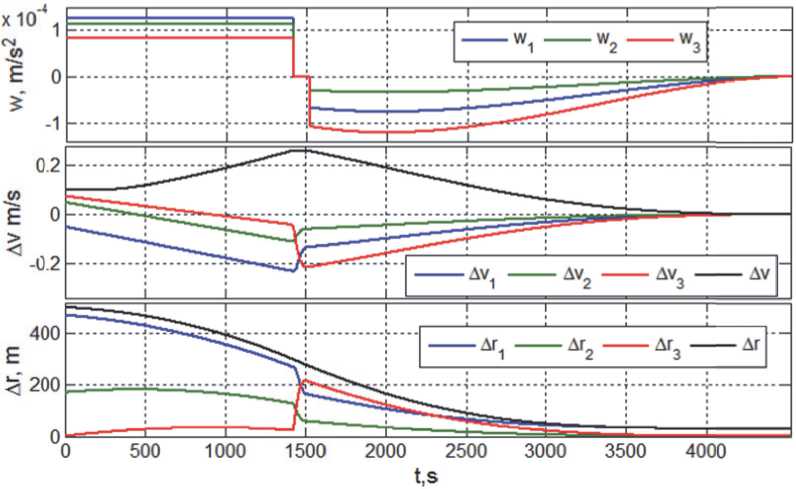
Рис. 6. Закон наведения КРМ в поступательном движении с разворотом его корпуса

билизации не хуже нескольких угловых секунд, что вполне достаточно.

Пусть дальность до цели измеряется лазерными дальномерами с периодом Tp = 1 с. Для оценки точности стабилизации закона наведения КРМ в поступательном движении предположим, что СКО погрешности измерения дальности оb = 0.05 м при Ar(t) > 300 м и по завершению разворота корпуса КРМ при Ar(t) < 300 м СКО такой погрешности измерения оb = 0.01 м. Погрешности стабилизации дальности ЗА ri при реализации указанного закона наведения, полученные при компьютерной имитации, представлены на рис. 7, а на рис. 8 приводятся изменения компонен- тов Pi вектора тяги ДУ при цифровом управлении с дискретностью по уровню de = 0.01 Н. На рис. 9 – 11 детально представлены изменения компонентов вектора погрешности дальности и вектора тяги ДУ, а также тяги всех восьми РД при завершении сближения и стабилизации.

При широтно-импульсном управлении ДУ с ШИМ тяги каждого из 8 РД важное значение имеет параметр T m модуляционной характеристики t _pr ( T m ) , который определяет минимальный импульс тяги РД IP _pr = T m P^m на полуинтервале времени t е ^[ t r , t r +1 ) , t r +i = t r + T U . При T = 4 с, T_m = 0.25 с и P^m = 0.5 Н минимальный импульс тяги РД принимает значение IP _pr = 0.125

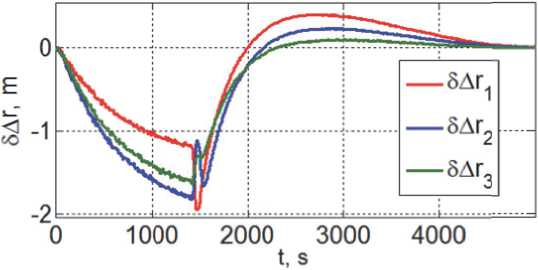
Рис. 7. Погрешности стабилизации дальности

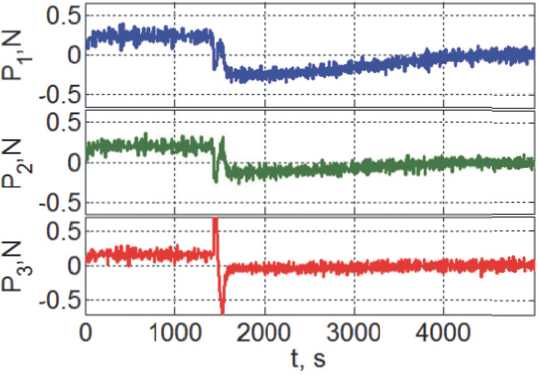
Рис. 8. Компоненты вектора тяги ДУ

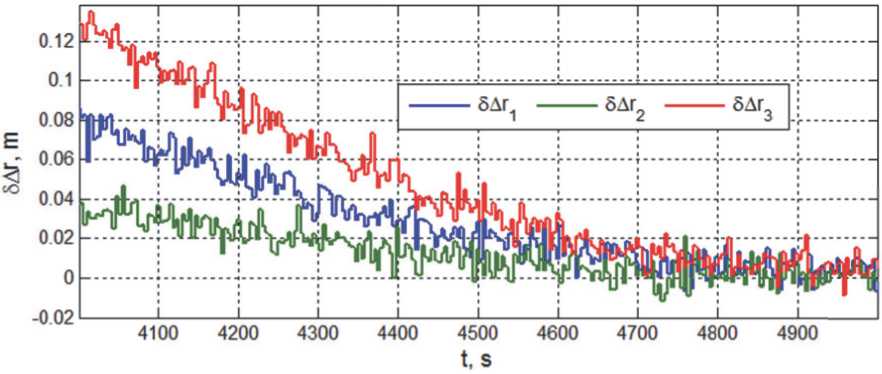
Рис. 9. Изменения погрешностей дальности при завершении сближения и стабилизации

Нс. С другой стороны, такому минимальному импульсу тяги при цифровом управлении РД соответствует расчетная дискретность квантования его тяги по уровню dе = IPpr /TU = 0.03125 Н. Выполненная компьютерная имитация показала близость значений погрешности стабилизации дальности при реализации синтезированного закона наведения КРМ как при широтно-импульсном управлении реактивными двигателями с параметрами TU = 4 с, тт = 0.25 с и Pm = 0.5 Н, так и при цифровом управлении с дискретностью de = 0,03 Н квантования их тяги по уровню. В обоих вариантах на интервале времени t е [4250,5000] с система управления движением КРМ обеспечивает стабилизацию его положения относительно пассивного космического объекта с точностью не хуже 0.3 м.

ЗАКЛЮЧЕНИЕ

Разработана стратегия пространственного наведения и управления движением КРМ, апробированная в первоочередной задаче заверше-

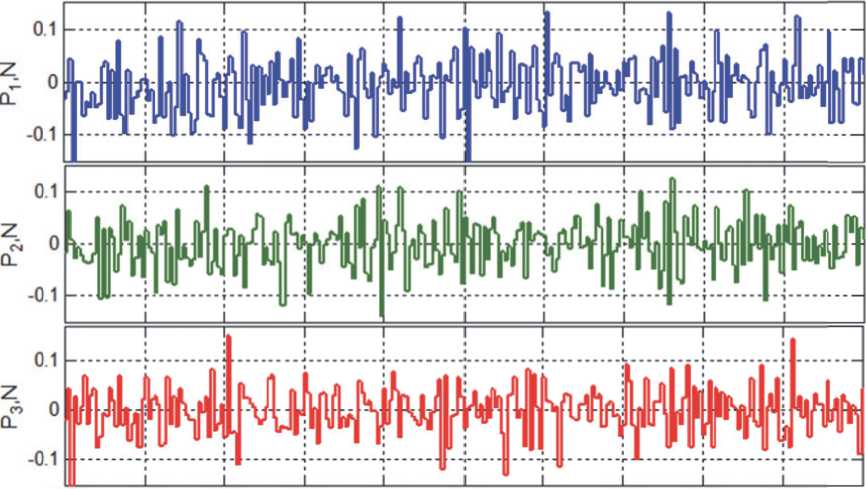
4000   4100   4200   4300   4400   4500   4600   4700   4800   4900

t, S

Рис. 10. Изменения компонентов вектора тяги ДУ при завершении сближения и стабилизации

0.1

О 1 L........!.........J..........!..........L.........!.........J..........I..........I.........!.........

^ _ПЫ#МЫ1^^

, 01L........!.........J.........|..... r-!.........J.........1..... -I.........!........-I

, 0.11-........(.........J..........!..........L.........}.........J..........!..........1.........1.........

^ _nj/lMi4lM^>^^

, 0.11—......}.........J-........4......... 1.........).........J.....     L 1.........

" o wll^dA|#!lMklil|r^^

4000   4100   4200   4300   4400   4500   4600   4700   4800   4900

t, S

Рис. 11. Изменения тяги восьми РД при завершении сближения и стабилизации ния сближения свободнолетающего робота с вращающимся пассивным объектом (целью) в дальнем космосе, когда можно пренебречь внешними возмущениями. Представлены создан- ные законы наведения и дискретные алгоритмы управления движением, а также результаты компьютерной имитации процессов при завершении сближения КРМ с целью и последующей стабилизации его положения относительно подвижного ПКО. Приведены оценки потребных ресурсов системы управления КРМ в отношении характеристик измерительных подсистем и исполнительных органов – минимально-избыточного кластера силовых гироскопов (гиродинов) с цифровым управлением и двигательной установки на основе восьми реактивных двигателей малой тяги как с широтно-импульсным, так и цифровым управлением, при которых обеспечивается требуемая точность системы управления движением робота-манипулятора.