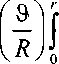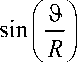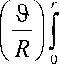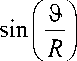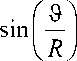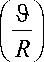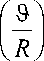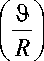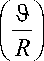Неизотермическое стохастическое смазывание тазобедренного сустава человека с различными частотами и амплитудами

Тазобедренный сустав в синовиальной оболочке представляет собой настолько сложную систему, что даже современные технологии не могут полностью повторить ее. В этой системе используется относительное скольжение гладких сферических поверхностей для обеспечения вращения конечности при приложении к ней различно направленных и зависящих от времени нагрузок.

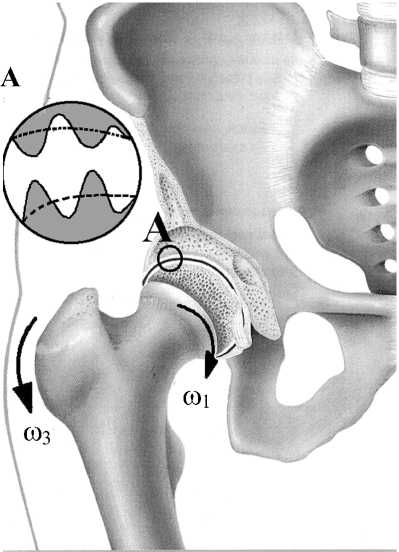
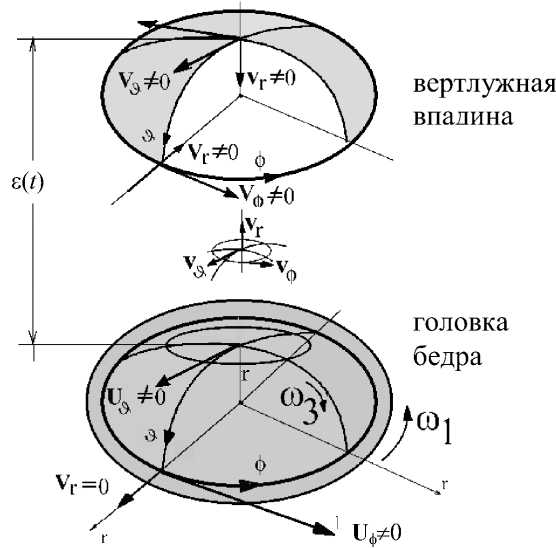
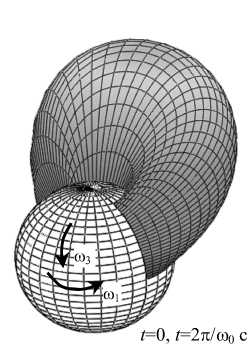
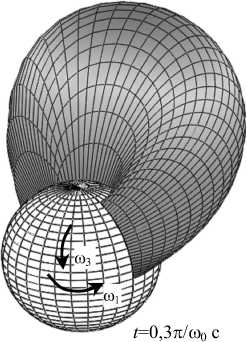
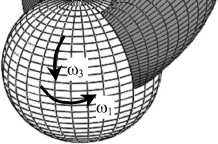
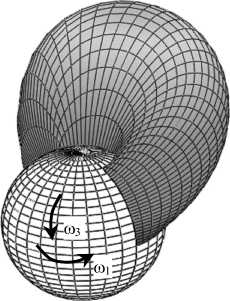
В данной работе предполагается, что сферическая головка бедра совершает вращательные движения вокруг двух осей с различными угловыми скоростями, см. рис. 1. Символом ϕ обозначена окружная координата, символом r – координата в

а

б

Рис. 1. Вращательное движение головки бедра в двух направлениях: а) общий вид, б) вид в деталях

направлении высоты зазора, символ ϑ обозначает меридиан костной поверхности вращения, или долготную координату. В работах [1, 5, 9] обсуждаются гидродинамические и механические параметры тазобедренного сустава человека. Как правило, там используются как аналитические, так и численные методы.

В работах [3, 6, 13, 14, 18, 24] исследуются силы трения в различных суставах человека для различной геометрии соприкасающихся костных поверхностей при изменяющейся высоте суставного зазора и несимметричном течении синовиальной жидкости. В вышеупомянутых работах [1, 5, 7, 8, 9, 12, 19, 20, 21, 23 ] не рассматривалось периодическое движение с различными частотами головки бедра и вертлужной впадины тазобедренного сустава человека. Также не принималось во внимание вязкоупругое смазывание при случайных условиях. Новизна данной работы состоит в вычислении нагрузки в тазобедренном суставе человека для шероховатых поверхностей кости и хряща, которые смазываются благодаря периодическому течению с различными частотами и амплитудами.

При несимметричном течении синовиальной жидкости три компоненты v ϕ , v r , v ϑ скорости жидкости по направлениям ϕ , r , ϑ зависят от переменных ϕ , r , ϑ и времени t . Давление p и вязкость синовиальной жидкости зависят от ϕ , ϑ , t . Высота ε зазора есть функция переменных ϕ , ϑ и t . Полученное в данной работе решение задачи о смазке дает давление и нагрузку для неньютоновой синовиальной жидкости во втором порядке точности. Предполагается, что колебания с различными частотами и амплитудами в окружном и меридиональном направлениях происходят в синовиальной жидкости и на поверхностях головки бедра и вертлужной впадины. Учитываются случайные изменения высоты зазора между костями.

• 2.    Основные уравнения

В тазобедренном суставе человека синовиальная жидкость течет между головкой бедра и вертлужной впадиной. Задача о смазке в суставном зазоре будет решена с помощью уравнения сохранения импульса, уравнения непрерывности и уравнения энергии [20, 21]:

Div S = p dv/dt, div v =0, p d(cvT)/dt = div(к grad T) = div(vS) - v Div S.

Кроме того, общее определяющее соотношение Ривлина и Эриксена во втором порядке точности записывается в следующем виде [2, 15, 16, 17]:

S = - p 1 + п А 1 + а ( А 1 ) 2 + в А 2 ,

где S – тензор напряжений, p – давление, I – единичный тензор, A 1 и A 2 – первые два тензора Ривлина - Эриксена и п , а , в - три материальные константы ( п - динамическая вязкость). Через T обозначена температура, κ – теплопроводность синовиальной жидкости, c v – теплоемкость синовиальной жидкости. Через A 1 и A 2 обозначены симметричные матрицы, определенные в [15, 16, 17]:

A 1 = L + L ^T , A 2 = grad a +(grad a) ^T + 2 L ^T L , a = L v +, L = grad v , L ^T = (grad v ) ^T , (3) где v – скорость (м/с), t – время (с) , a – ускорение (м/с²). Сферическая головка бедра движется относительно вертлужной впадины в окружном направлении ф и меридиональном направлении 9 . Поверхности вертлужной впадины и головки бедра колеблются в направлениях ф и 9 с различными амплитудами и частотами. Кроме того, вертлужная впадина колеблется в направлении высоты зазора. Такое движение суставных поверхностей вызывает течение синовиальной жидкости в суставном зазоре. Угловую скорость вращения головки бедра в окружном направлении обозначим через ю 1 , в меридиональном направлении - через ю ₃. В суставном зазоре имеется несимметричное нестационарное течение синовиальной жидкости, при этом жидкость проявляет вязкоупругие и нестационарные свойства. Центробежными силами пренебрегаем. Введем следующие обозначения: U = ю 1 R - окружная скорость, p = p ₀ -постоянная плотность синовиальной жидкости, п = П 0 П 1 - переменная вязкость, п 0 -характерное значение динамической вязкости, £ - зависящая от времени высота суставного зазора, R – радиус головки бедра, t 0 – характерное значение времени; течение жидкости предполагается изотермическим.

Предполагаем, что произведение чисел Дебора ( Deborah ) De = Рю 1 / п 0 и Струхала Str= RU/t 0 , то есть De Str, и произведение числа Рейнольдса Re= p U s / n o , безразмерного зазора у и числа Струхала, то есть ReStr y , являются величинами одного порядка и что De Str >> De [14]. Учтем эти оценки в основном уравнении течения тонкого слоя в сферическом суставном зазоре [14]. Пренебрегая величиной y=s / R * 10 ^{- 3} и центробежными силами, получим в вышеупомянутых предположениях следующие уравнения в сферических координатах ф , r , 9 [12, 19, 20, 21, 22]:

^d v ф

5t

1    ap + n         )

p R sin f ^- !*   ^{pd r} I   ^{8 r} J

( R J

, в ^{d v} ф p 5 t 5 r ² ,

0 =*,

5 r dv,     1 dp  n d f  dvs)  в d3 v„

- =+ n- +Jdt     p d9   p dr (   dr J  p dtdr2

5 vф

—- + R sin

5ф

9)5 vr 5 — I™—+ ~~ R ) 5r 59

I 9

Rv, sin — ⁹ I R

= 0,

5 r

K IT 1+n

I 5 r J

f^ 1

I ^{5 r} )

+

1 5 v ₈ 1 2

I ^{5 r} )

= 0,

где 0 < ф <  2 n 0 i , 0 <  0 i <1, b m = n R /8 < 9 < n R /2 = b s , 0 <  r < £ , £ - высота зазора. Члены с множителем в описывают влияние вязкоупругих свойств синовиальной жидкости на эффекты смазки. Конвективными членами пренебрегаем. В левых частях (4) и (6) оставлены только производные по времени от компонент скорости. В уравнении энергии учтены диссипативные члены.

• 3.    Метод решения задачи о периодическом смазывании

Так как уравнения (4) - (7) линейны, то можно разделить стационарное и нестационарное течения жидкости. Учтем касательные и вертикальные ускорения точек суставной поверхности. Запишем компоненты скорости жидкости и давление в виде сходящихся рядов [3, 11]: то v = v^ (ф, r, 9) + ^ v( k) (ф, r, 9) exp(i k ^0t), i = ф, 9,(9)

k = 1

то vr = vro)(-, r, 9) + ^ vrk )(ф, r, 9)exp(i k to0t),(10)

k = 1

то

T = T(0) (-, r, 9) ■ У T(k) (-, r, 9) exp(i k^t),(11)

k=1 то p = p (0)(ф,9) + ^ p(k )(ф, 9)exp(i k ^0 t ).

k = 1

Через to o обозначена частота колебаний (с^-1); это частота периодических возмущений нестационарного течения жидкости. Через i = V-1 обозначена мнимая единица. Неизвестные функции с верхним индексом (0) есть компоненты скорости и давление для стационарного течения не вязкоупругой жидкости. Неизвестные функции с верхним индексом ( k ) для k = 1,2, 3,^, являются поправками, обусловленными нестационарными вязкоупругими свойствами жидкости. Высота зазора имеет следующий вид [4, 10]:

то s tot =£(0) +£ + 5^£(0)(ф, 9) + ^£( k )(ф, 9)exp(i kto rt) + 5,            (13)

k = 1

где 5 ( ^ ) - случайная добавка, возникающая из-за колебаний и неровностей поверхности, отсчитываемых от среднего уровня, ^ - случайная величина, ~ -нестационарное возмущение высоты зазора, вызываемое нестационарными условиями работы сустава, £ ^{( k )} - не зависящие от времени коэффициенты в возмущениях высоты зазора, £ ⁽⁰⁾ - начальное значение высоты зазора, £ _tot - общая высота зазора^ _r - частота колебаний в направлении высоты зазора. Детали метода решения см. в Приложении 1.

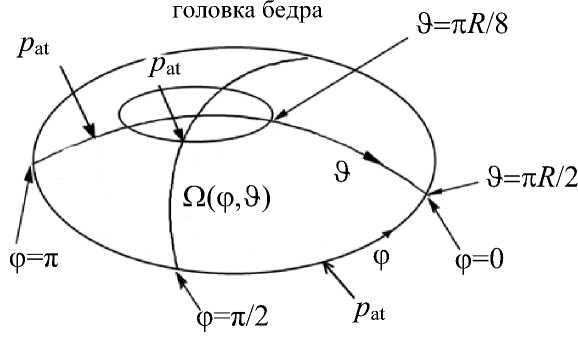
Рис. 2. Расположение области смазывания сферической головки бедра

• 4.    Граничные условия

Расположение области смазывания Q : 0 < ф <  п , п R /8 < 9<п R /2 показано на рис. 2. Вертлужная впадина движется в окружном ф и меридиональном 9 направлениях. Кроме того, учитываем зависящее от времени касательное ускорение точек поверхности головки бедра. Касательные (в направлениях ф и 9 ) компоненты скорости ( U ) на поверхности головки бедра и компоненты скорости ( V ) на поверхности вертлужной впадины, а также температура имеют следующий вид: то                                                то

U i = U o + Е U k exp ( i ^к to u t ) , V = £ V ik exp ( i к toj ) , к = 1                                       к = 1

T = T o при r = 0, T 1 = f ⁽ o ) + Е T_k exp ( i к to u t ) при r = £ к = 1

U           V                   f ( k )

Uik = -ТГ, Vik = T = const, Tk = -TT UфД=ю10 R sin (9 / R), U,-x to30 R sin ф , kk   k где Uik – не зависящие от времени амплитуды касательных колебаний на поверхности головки бедра, i = ф, 9, к = 1, 2, 3,...., Vik, fк) - не зависящие от времени амплитуды колебаний касательной скорости и температуры на поверхности вертлужной впадины, i = ф, 9; к = 1, 2, 3,.... Черезf0) обозначена не зависящая от времени часть температуры вертлужной впадины. Через гофv, гофu, to9v, to9u обозначены различные частоты колебаний вертлужной впадины (нижний индекс v) и головки бедра (нижний индекс u) в направлениях ф и 9. Эти частоты отличаются от частоты to0, соответствующей синовиальной жидкости. Окружная скорость на поверхности сферической головки бедра не зависит от ф и достигает максимального значения to1 R на экваторе при 9 = Rп/2, а нулевого значения - на полюсе при 9 = 0 или 9 = Rп. Меридиональная скорость на поверхности сферической головки бедра не зависит от 9 и достигает максимального значения to3R при ф = п/2, а нулевого значения - при ф = 0 и ф = п. Следовательно, не зависящие от времени части окружной и меридиональной скоростей для головки бедра при стационарном движении имеют вид:

U _{ф 0} = to 1 R sin( 9 / R ), U _{9 0} =to 1 R sin( ф ), 0 <9< R п , 0 <ф<п .         (15)

Обозначим через го ₁ и го _1о угловую скорость и поправку к ней для вращения головки бедра в ф - направлении; через го ₃ и го ₃₀ - угловую скорость и поправку к ней для вращения головки бедра в 9 -направлении. Внутри суставного зазора на скорости (9, 10) накладывается граничное условие (14) 1 . Приравниваем первые стационарные члены правой части (9), представляющие собой компоненты скорости жидкости, стационарным членам правой части (14)₁. Компоненты скорости жидкости на поверхности неподвижной вертлужной впадины равны нулю. На поверхности головки бедра равна нулю только вертикальная компонента скорости жидкости, так как учитываются вязкие свойства жидкости. Компоненты скорости жидкости на поверхности головки бедра в направлениях ϕ и ϑ равны соответствующим компонентам скорости головки бедра. Граничные условия на стационарную часть компонент скорости жидкости для i = ф , 9 ; к = 1, 2, 3,... на поверхности головки бедра при r = 0 и на поверхности вертлужной впадины при r = £ имеют следующий вид:

vф0) (ф, r = 0,9) = Uф0 (9), v90) (ф, r = 0,9) = U90 (ф),(16)

v(0) (ф, r = 0,9) = 0, T(0) (ф, r = 0,9) = T0,(17)

v1(0)(ф,r = £,9) = 0, при i = ф, r,9; T(0)(ф,r = £,9) = f(0).(18)

Теперь наложим нестационарную часть граничных условий (14)₁ на нестационарную часть компонент скорости (9, 10, 11). Однако сопоставить нестационарные члены в рядах (14)₁ и (9, 10, 11) невозможно, так как частоты в обеих частях уравнений различны. Поэтому ряды в правых частях (14)₁, (14)₂, описывающие колебания с известными амплитудами U _{ф к} , U _{9 к} , V _{ф к} , V _{9 к} , T k и известными частотами го_{ф и} го₉ u , го_{ф v} го_{9 v} , преобразуются (см. Приложение 2) в ряды с некоторыми новыми, неизвестными, амплитудами U * _к , U 9 _к , V t , V _9k , T * и известной частотой го ₀, отвечающей синовиальной жидкости. В Приложении 2 также приведено вычисление амплитуд U * , V k [2,9]. В результате вычислений новые неизвестные амплитуды U ф _к , U 9 _к , V^ , V _9k, W k *, T получаются как функции известных амплитуд U _ф к , U » к , V _р к , V 9 к , W k , Т_к , известных, экспериментально измеренных, частот го_ф u , го₉ u , го_{ф v} , го_{9 v} , го _r и известной частоты го ₀, отвечающей колебаниям синовиальной жидкости [2]. Например, через го_ф u , го₉ u обозначены частоты колебаний головки бедра в ф и 9 направлениях. Через го_{ф v} , го_{9 v} обозначены частоты колебаний вертлужной впадины в ф и 9 направлениях. Теперь можно приравнять нестационарные члены в правых частях (9, 10) нестационарным членам в правых частях (14)₁, (14)₂. Граничные условия на нестационарные поправки к температуре и к компонентам скорости i = ф , 9 ; к= 1, 2, 3,... имеют на поверхности головки бедра при r = 0 и на поверхности вертлужной впадины при r = £ следующий вид [3, 11]:

v")(ф, r = 0,9) = Uфк(Uфк,Гофu), V9к)(ф, r = 0,9) = U9к(U9к,го.и),(19)

vrк )(ф, r = 0,9) = 0, T(к )(ф, r = 0,9) = 0,(20)

viк) (ф, r = £,9) = ^к(^,го^), при i = ф,9, T(к) (ф, r = £,9) = T*.

Высота суставного зазора со временем меняется. Вертикальная компонента скорости жидкости на поверхности вертлужной впадины равна производной по времени от высоты зазора. Следовательно, используя (13), получаем:

∞

Е vrk) (ф, r = s, 9) exp (iktoot) = -^o- = k=1

∞∞∞

= E s ⁽ k ) i k to r exp ( i k to r t ) = i ^ W_k exp ( i k to r t ) = i ^ W k * exp ( i k to ₀ t ) .

k=1                                     k=1

Приравнивая амплитуды в обеих частях выписанных выше рядов, находим:

vrk) (ф, r = s, 9) = i W (Wk, tor), Wk = s(k)ktor(23)

для k = 1, 2, 3,... , s ^{( k} ) = B e s ⁽⁰⁾/ k ⁵, где 0 <  B e <1. Безразмерный коэффициент B e отвечает за не зависящие от времени возмущения высоты зазора. Не зависящая от времени средняя высота зазора с возмущениями имеет вид [3]:

vrk) (ф, r = s, 9) = i W (Wk, tor),   Wk ^ s(k)ktor(23)

где

s ⁽⁰⁾( ф , 9 / R ) As x cos ф sin 9 / R + As y sin ф sin 9 / R - As z cos 9 / R - R +

+[(Asx cosфsin9/R + Asy sinфsin9/R - Asz cos9/R)2 +

+ ( R + s min )( R + 2 D + s min )]

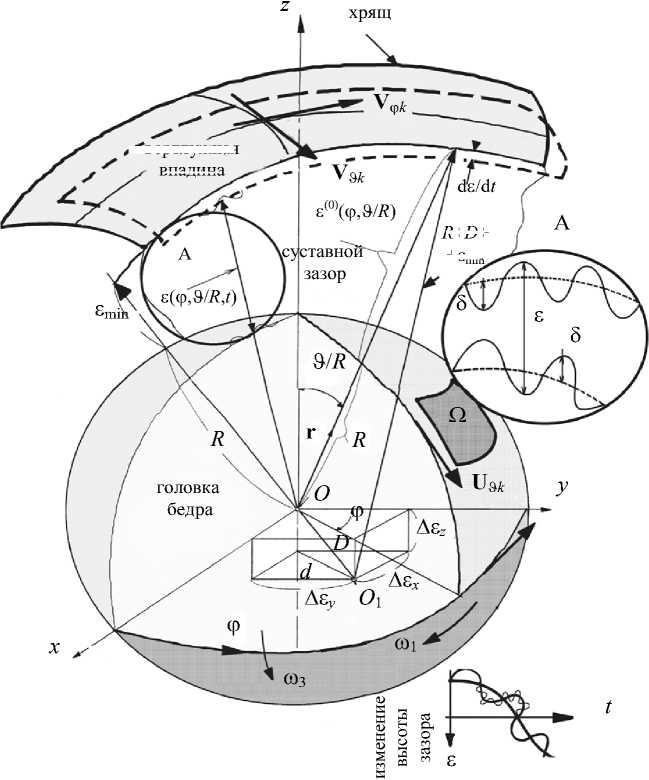
и t s - средний временной период возмущений суставного зазора, ^ e - вещественная часть комплексного числа. Центр сферической головки бедра расположен в точке O (0, 0, 0), а центр сферического хряща - в точке O 1 ( x -As _x , y -As y , z + As _z ). Эксцентриситет обозначен через D (см. рис. 3). Вывод соотношения (25) приведен в Приложении 2 (см. уравнения A2.20 - A2.22).

• 5.    Стохастические уравнения для распределения давления и сил трения

Нахождение компонент v^, v ^k ) скоростей жидкости для граничных условий (16), (18) 1 , (19) и для постоянного значения динамической вязкости в направлении высоты зазора приведено в Приложениях 1 и 3. Граничные условия (16), (18) 1 , (19), (21) 1 добавляются к системе уравнений (A1.1) - (A1.3), описывающих стационарное течение, а граничные условия (19), (21) 1 - к системе уравнений (A1.6) - (A1.8) для поправок (см. Приложение 1). Тогда получаем искомые компоненты скорости стационарного течения v _ф ⁽⁰⁾, v ₉ ⁽⁰⁾ и поправки v _ф ^{( k} ) , v ₉ ^{( k} ) для k = 1, 2, 3,..., вызванные вязкоупругими свойствами и нестационарностью течения. Результаты вычислений приведены в Приложении 3.

Подставим функции v _ф ⁽⁰⁾, v ₉ ⁽⁰⁾ (см. (A3.1), (A3.2) в Приложении 3) в уравнение непрерывности для стационарного течения (A1.4) и подставим найденные функции v _ф ⁽ k ) , v ₉ ⁽ k ) ( k = 1, 2, 3,..., см. (A3.3), (A3.4)) в уравнение непрерывности для поправок (A1.9). Тогда после интегрирования по r получим компоненту скорости v_r ⁽⁰⁾ в направлении высоты зазора и получим поправки v_r ^{( k} ) ( k = 1, 2, 3,...) к этой компоненте (см. Приложение 4). Учитывая граничные условия (17) 1 , (18) 1 , (20) 1 , (23) для v_r ⁽⁰⁾ (см. (A4.1)) и поправок v_r ^{( k} ) ( k = 1, 2, 3,^) к ней (см. (A4.2)), получим модифицированное уравнение Рейнольдса для давления p ⁽⁰⁾ и поправок к нему p ^{( k} ) ( k = 1, 2, 3,...). Детали вычислений приведены в Приложении 5.

R + D +

°mm вертлужная впадина

Рис. 3. Изменение высоты зазора со временем, центр сферической головки бедра и вертлужной впадины, значения скорости на границе

Модифицированное уравнение Рейнольдса для стационарного течения синовиальной жидкости без вязкоупругих свойств определяет искомое давление p ⁽⁰⁾ и имеет вид:

cosеc R

3) 5   S31^1R /дф ^ПоП1

5 p⁽⁰⁾ ₊ r 5 S 3 5 p⁽⁰⁾

дф     53[п0П1 53

sin— > =

R

f 3) = 6 to, R sin

1     (R ) дф

5s 2 ■ ( \ д Г . f3) — + 6м;R sin (ф) — s sin — дф 3 v ’ 53 L (R)

в Q : 0 < ф < п , n R /8 <3 < п R /2.

Далее рассмотрим модифицированные уравнения Рейнольдса для поправок p ^{( k )} ( k = 1, 2, 3,...) к давлению, вызванных периодическим течением жидкости с вязкоупругими свойствами. Эти уравнения выведены в Приложении 5 (см. (A5.6)). Умножая (A5.6) на exp ( i k to ₀ 1 ) и приравнивая вещественные части, получим следующую последовательность модифицированных уравнений Рейнольдса:

1 (9) 5 — cosec I — I— R V R /5ф

s ³ 5 P ck

. П ka  ⁵ ф.

+ 6 [ U ф к . ( « 3 ) + V k ]

+R

s ³ 5 P ck

. П ka 59

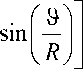
- 12 W k R sin

^cos ( к....t ) + ^{к гор 5} ,._: X„) 5ф               12 5ф^ ⁿ k’

• cos ( k ro ₀ t ) + 6 [ u * . ( a ) + V k ] R •

59

s sin

-

* 5s ( . 9\* 5s 12 Vk —+R sin— Vt— фk 5ф   | R) 9k59

Ha 5

12 59

s 3 X _n .

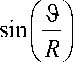
для к = 1, 2, 3,..., 0 < ф <  2 п 0 1 , 0 < 0 1 <  1, b m = п R /8 < 9< п R /2 _ b s , 0 <  r < s и

P_ck = ^ e[Р ⁽ k ) exp( i к ^ю о t )],

_ ^{sin( k} ® 0 t )

X n к _ n ka

+ cos( к го ₀ t )

П kb

— = « e П ka

⁽¹1 In к /

_ An

I n к Г ’

1          I 1 )

— = ^ m — П kb     Ь к /

—

к го ₀ Р

n к = П0П1 + ik AP,  |n к |2 = (П0П1 )2 + (k Ю0Р)2.

Уравнение (27) определяет поправки P ck к давлению, вызванные нестационарным течением синовиальной жидкости с вязкоупругими свойствами. Новые амплитуды имеют вид (см. Приложение 2):

и * - ^U \ v tz*    V 0_ v nz* - ^s__ B e ^го0 c

U ik = к5 Siuk , Vik = к5 S'vk ’ W = к4 Srk ’ где i = ф, 9 и к = 1, 2, 3,_ Функции Siuk, Sivk, Srk зависят от частот Гофv, Гофи, го»v, го»и, гог (см. Приложение 2). В частном случае roiv = roiи = го0 и гоr ^ го0 находим Siuk = 1, Sivk = 1, следовательно, Uik = Uik, Vik = Vik и Srk *1, где 0 < Be << 1 (см. Приложение 2, (A2.18)). Уравнения (27) при k = 1, 2, 3,... дают окончательные модифицированные стохастические уравнения Рейнольдса для поправок [3]:

J E ( s ³) 5 E ( P ck ) | _{+ R} ^f E ( s ³) 5 E ( P ck ) sin 9, . n ka    5ф J ⁵⁹ 1 n ka ^{59 R}

1     5

^э 5ф

R sin— ^ф R

(             sin ( k ro„ A

—12... RBe Ism Э s S„ —(-^)

V ^R /          k

—

12 f V ; 0

5E (s) 5ф

+ R\ sin— | V L

V R ) ⁹⁰

5 E ( s )

_x ^{cos ( k ro} 0 t ) + 6 k ⁵

I 9)_|T/ ^ro 10 ^R I sin- | ⁺ V 0

V R /

" J 5 E ( s ) cos( k ro 0 t ) _ 1 5ф       к⁵

+

ro0p0 5

12 к ⁴ 5ф

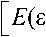
³) X n k ]

,+

+6R[ro,0 R ( sin ф) + V90 ]•

^{E ( s )sin} R

cos (kro0t) + ГО0Р0 5 к5      12к4 59

^{E ( s 3 )} X ^, sin R,

где 0 < ф <  2 п0 1 , 0 < 0 1 <  1, b m _ п R /8 < 9 < п R /2 _ b s , 0 <  r < s . При го _r = ro ₀ получим S rk = 1, где 0 <  B <<1. Уравнение (30) определяет средние значения для поправок к давлению E ( P ck ). Среднее значение суммарного давления и оператор осреднения имеют следующий вид [3]:

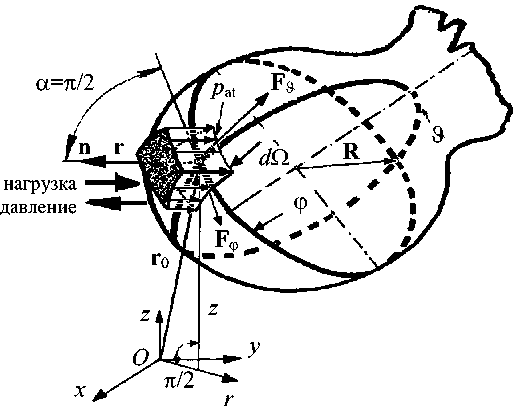
Рис. 4. Расположение сил трения в окружном и меридиональном направлениях

то

E (p) = E [ pm] + У E [ P ], k=1

+to

E (*) = j ( • ) x f ( 6 ) d 6 , f ( 6 ) -<

-TO

32 c ⁷

(c2-62 )3

при - c < 6 < + c , при |б| > О ,

где f - плотность распределения случайной шероховатости хряща. Через c обозначена половина диапазона изменения случайной толщины. Функция f обращается в нуль при c = ± 3 с , где с - стандартное отклонение. После вычислений находим:

+TO

E ( _е ) = | £ f ( 6 ) d 6 = Г ₅ £ ⁽⁰⁾

-то

+TO

E (£³) = р f ( 8 ) d 8= ( Г , £<⁰⁾ /(1 + 3 р ² ), 0 ■    '^С0. = Р< -, (32)

I £( )

-то где Г5 ^ 1+Гy. На рис. 4 показано распределение давления p(ф, 9) на сферической поверхности головки бедра (ф и 9 - сферические координаты). Полная нагрузка на головку бедра получается следующим образом:

C_to t = jj E [ p ( ф , 9 )] d Q ( ф , 9 ), О ( ф , 9 )

где JJ - интеграл по поверхности головки бедра. Элемент площади в интеграле имеет

Q вид:

d Q

d r0 x£r 5ф 59

r = R

d ф d 9

при r ₀ = i x + j y + k z ,

где x = r cos ф sin(9/R), y = r sin ф sin(9/R), z = r cos(9/R) 0 < r< R.       (35)

Через r ₀ обозначен радиус-вектор точки поверхности головки бедра (см. рис. 4); 0 <  ф < 2 п c 1 , 0 <  c 1 < 1, п R /8 <  9 < п R /2. Подставляя (35) в (34), получим:

d Q = R ² sin( 9 / R ) d ф d( 9/ R ).

На рис. 4 показано расположение сил трения в направлениях ф и 9 . Окружная и меридиональная компоненты силы имеют вид:

„ ( Sv. 3                  „ ( Sv.

F . - jj   П p ^    d П ( Ф , 9 ), F . - fj   П p ,'    d П ( ф , 9 ).       (37)

П ( ф , а ) \     ^d r 7 r =e                     П ( ф , 9 ) к     ^d r 7 r =e

• 6.    Экспериментальные измерения

• 7.    Численные расчеты

  Распределение давления p ⁽⁰⁾ и поправки к нему p ⁽¹⁾, p ⁽²⁾, p ⁽³⁾,... определялись в области смазывания Q . Суммарное давление равно атмосферному p_at на границе области Q , показанной на рис. 3 и на основе медицинской информации, определяемой неравенствами Q : 0 < ф < п , п R /8 <а ₃ = 9 <п R /2. Это сечение сферического углубления. Численные расчеты проводились для области Q , R = 0,0265 м, го 1 = 1,40 с^-1, го ₃ = - 0,45 с ^{- 1}, го о = 500 с ^{- 1}, Ю 10 = 0,100 с, Го з0 = 0,025 с, Де x = 2,5 ? м, Де _у = 0,5 ? м, Де _z = 2,0 ? м, п о = 0,15 Па, р₀=1000 кг/м³. Минимальное значение высоты зазора равнялось e _min = 4,8 ц м, максимальное значение высоты зазора равнялось e _max = 10,50 ц м. Учитывалась измеренная шероховатость поверхностей. Значения давления вычислялись в следующие моменты времени: t = 0 с, t = 0.3 п / ю ₀ с, t = п / го ₀ с, t = 1.7 п / ю ₀ с, t = 2 п / ю ₀ с,.... Вначале были проведены численные расчеты без учета вязкоупругих свойств синовиальной жидкости, то есть при р ₀ = 0,00000 Па² и р ₀ = 0,00020 Па².

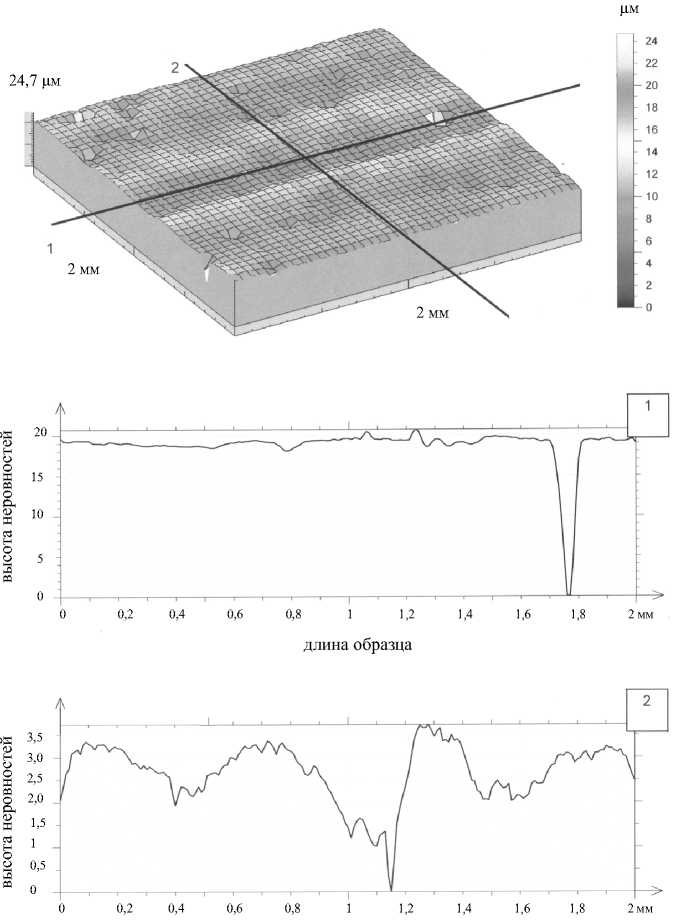
Плотность распределения высоты суставного зазора находилась путем экспериментальных измерений шероховатости образцов хряща и соответствующих стандартных отклонений. Измерения выполнялись с помощью лазерного микродатчика, установленного на аппаратуре Rank Taylor Hopson Talyscan 150 и управляемого посредством компьютерных программ Talyscan Expert и Microsoft Exel . Измерения проводились для 29 образцов; получены параметры S t , S z , S_a шероховатости поверхности (в мкм). Здесь: S t - разность максимальной высоты и максимальной глубины на поверхности головки бедра, S z - среднее арифметическое пяти максимальных высот и пяти максимальных глубин, S_a - стандартное отклонение для плотности распределения шероховатости поверхности хряща. Измеренные значения S t находятся в интервале от 9,79 мкм до 24,7 мкм. Измеренные значения S z находятся в интервале от 8,52 мкм до 14,7 мкм. Окончательно вычисленные значения S a находятся в интервале от 0,78 мкм до 1,96 мкм. На рис. 5 показана карта поверхности нормального суставного хряща с высотой неровностей до 24,7 мкм и сечения 1 и 2 этой поверхности. Образец имел 2 мм в длину и 2 мм в ширину.

На вертлужной впадине принимались следующие амплитуды колебаний касательной скорости: V _{ф 0} = 0,001 м/с, V _{9 0} = - 0,0002 м/с. Коэффициент возмущений высоты зазора принимался равным B e = +0,0002. Принимались во внимание случайные эффекты для 0 < р < 1.

Численное нахождение зависящего от времени распределения давления проводилось с помощью уравнения (30), а высоты зазора с помощью (24, 25). Результаты показаны на рис. 6, 7, 8, 9. Временной период возмущений составлял t = 2 л/го о .

длина образца

Рис. 5. Измеренная поверхность нормального хряща в тазобедренном суставе и два ее сечения

На рис. 6 показано изменение со временем распределения давления для ℘ = 0 и β 0 = 0. Стохастическое описание шероховатости хряща не принималось во внимание, так как ℘ = 0. Вязкоупругие свойства синовиальной жидкости не учитывались, так как β 0 = 0,0000 Па².

Для моментов времени t = 0, t = 0,3 π / ω 0 , t = π / ω 0 , t = 1,7 π / ω 0 , t = 2 π / ω 0 получены следующие значения нагрузки: 1292,7 Н, 1655,0 Н, 1306,5 Н, 936,7 Н, 1292,7 Н.

На рис. 7 показано изменение со временем распределения давления для ℘ = 0 и β 0 = 0,00020 Па². Стохастическое описание шероховатости хряща не принималось во внимание, так как ℘ = 0. Вязкоупругие свойства синовиальной жидкости учитывались, так как β 0 = 0,00020 Па².

Для моментов времени t = 0, t = 0,3 π / ω 0 , t = π / ω 0 , t = 1,7 π / ω 0 , t = 2 π / ω 0 получены следующие значения нагрузки: 1289,0 Н, 1839,1 Н, 1309,2 Н, 749,5 Н, 1289,0 Н.

P max =1,8 - 10 6 Па

C tot =1292,7 Н

1.5 [MPa]

0.75 [MPa]

P max =2,225 - 10⁶ Па

C tot =1655,0 Н

1.5 [MPa]

0.75 [MPa]

t^ с p max=1,812.106 Па

C tot =1306,5 Н

Рис. 6. Распределение давления в зазоре тазобедренного

; t=1,7n/ ю0 с pmax=1,390-106 Па Ctot=936,7 Н сустава, вызванное вращением сферической головки бедра одновременно в окружном ф-направлении и меридиональном 3-направлении. Случайные эффекты и вязкоупругость синовиальной жидкости не учитываются, так как р = 0 и р0 = 0. Вычисления проведены для ненулевых значений угловых скоростей «1 = 1,40 с-1 ,«3 = - 0,45 с-1, ненулевых значений возмущений угловых скоростей «10, «30 при нестационарном течении и для частоты возмущений высоты зазора «0 = 500 с-1, R = 0,0265 [м],  п = 0,15 [Пас], «о = 500 [1/с],  «1 = 1,4 [1/с], «з = 0,45 [1/с],

« 10 = 0 , 1 [ 1/с], ю_{3 0} = 0 , 025 [ 1/с], Р о = 0, р= 0, смазываемая поверхность = 20,38 [см²]

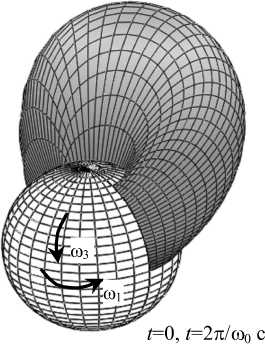
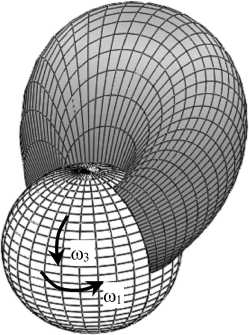
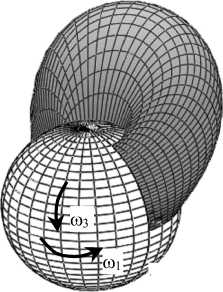
На рис. 8 показано изменение со временем распределения давления для р =1/3 и р ₀= 0. Стохастическое описание шероховатости хряща принималось во внимание, так как р = 1/3. Вязкоупругие свойства синовиальной жидкости не учитывались, так как р ₀ = 0,0000 Па².

Для моментов времени t = 0, t = 0,3 п / « ₀, t = п / « ₀, t = 1,7 п / « ₀, t =2 п / ю ₀ получены следующие значения нагрузки: 1258,1 Н, 1612,6 Н, 1270,8 Н, 909,5 Н, 1258,1 Н.

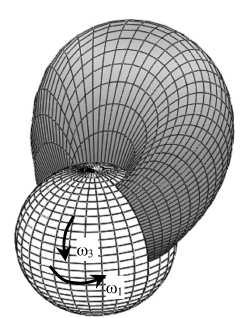
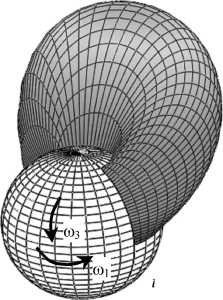
На рис. 9 показано изменение со временем распределения давления для р = 1/3 и Р о = 0,00020 Пас². Стохастическое описание шероховатости хряща принималось во внимание, так как р = 1/3. Вязкоупругие свойства синовиальной жидкости учитывались, так как р ₀ = 0,00020 Па².

Для моментов времени t = 0, t = 0,3 п / ю ₀, t = п / ю ₀, t = 1,7 п / ю ₀, t = 2 п / ю ₀ получены следующие значения нагрузки: 1254,7 Н, 1792,8 Н, 1273,4 Н, 726,4 Н, 1254,7 Н.

Легко видеть, что распределения давления и нагрузка, представленные на рис. 6, 7, 8, 9 для моментов времени t = 0 с и t = 2 п / « ₀ с, то есть для t = 2 к п / ю ₀ с и к = 0, 1, 2,..., имеют одинаковые значения. Распределения давления и нагрузка в моменты времени t = (2 к - 1) п / « ₀ с для к = 1, 2, 3, 4,... также имеют одинаковые значения.

1,5 [МПа]

t =0, t =2 n / m ₀ с P max =1,798 - 10⁶ Па

C tot =1289,0 Н

0,75 [МПа]

t =0,^{3 n / m} 0 с P max =2^,443 - 10⁶ Па

C tot =1839,1 Н

1,5 [МПа]

t= n / m 0 с

P max =¹,⁸¹⁵ ' ¹⁰⁶ Па

C tot =1309,2 Н

0,75 [МПа]

t=1,7 n / m ₀ с

P max =1,176 - 10⁶ Па

C tot =749,5 Н

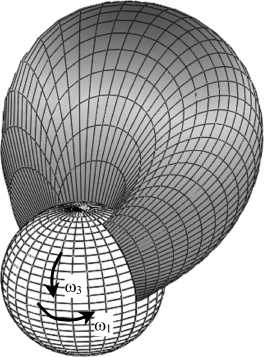
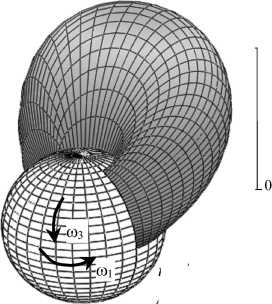
Рис. 7. Распределение давления в зазоре тазобедренного сустава, вызванное вращением сферической головки бедра одновременно в окружном ф -направлении и меридиональном Э -направлении. Случайные эффекты не учитываются, так как р = 0; вязкоупругость синовиальной жидкости учитывается, так как р ₀ = 0,00020 Па². Вычисления проведены для ненулевых значений угловых скоростей Ю [ = 1,40 с ^{- 1} , m 3 = - 0,45 с ^{- 1}, ненулевых значений возмущений угловых скоростей m ₁₀, m ₃₀ при нестационарном течении и для частоты возмущений высоты зазора m ₀ = 500 с ^{- 1}. R = 0,0265 [м], п = 0 , 15 [ Пас], m ₀ = 500 [ 1/с], Го ] = 1 , 4 [ 1/с], m 3 = 0 , 45 [ 1/с], m_{1 0} = 0 , 1 [ 1/с], m_{3 0} = 0 , 025 [ 1/с], р ₀ = 0 , 00020 [Пас²], р = 0, смазываемая поверхность = 20,38 [cм²]

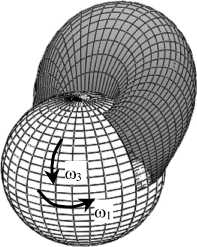
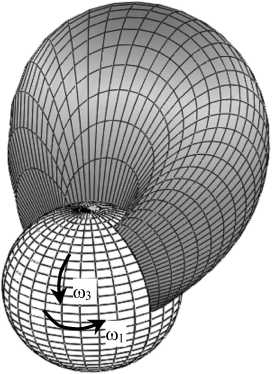
Верхняя левая иллюстрация на рис. 6-9 показывает распределение давления в начале и в конце периода возмущений движения сустава. Иллюстрации, отвечающие t = n / m ₀ на рис. 6-9, показывают распределение давления в середине периода возмущений движения сустава. Затем распределения давления возвращаются к показанному на первой иллюстрации.

Влияние случайных изменений высоты зазора и вязкоупругих свойств синовиальной жидкости на нагрузку показано на рис. 10 и обсуждается ниже.

На рис. 10 показано изменение нагрузки со временем в течение периода возмущающих эффектов (частота m ₀ = 500 с ^{- 1}) для четырех вариантов условий, отвечающих четырем случаям на рис. 6, 7, 8, 9: (1) р = 0, р ₀ = 0; (2) р = 0, р ₀ = 0,0002 Па²; (3) р = 1/3, р ₀ = 0; (4) р = 1/3, р ₀ = 0,0002 Па². Если р = 0, то случайные эффекты не учитываются. Если р ₀ = 0, то синовиальная жидкость является ньютоновской.

На рис. 11(a) показано изменение нагрузки со временем в течение периода возмущений при трех различных частотах возмущений: m ₀ = 100 с ^{- 1}, m ₀ = 500 с ^{- 1}, m ₀ =

1000 с ^{- 1} для ньютоновской ( в о = 0,00000 Па²) и вязкоупругой ( Р о = 0,00020 Па²) синовиальной жидкости.

На рис. 11(b) показано изменение нагрузки со временем в течение периода возмущений ( « ₀ = 500 с ^{- 1}) для следующих значений параметра р ₀, описывающего вязкоупругие свойства синовиальной жидкости: р ₀ = 0,00001 Па², р ₀ = 0,00005 Па², р ₀ = 0,00010 Па², р 0 = 0,00015 Па², р 0 = 0,00020 Па², р 0 = 0,00025 Па², р 0 = 0,00030 Па², р 0 = 0,00035 Па², р 0 = 0,00040 Па².

Размеры неровностей на поверхности хряща лежат в интервале от 0,2 р м до 0,9 р м. Поэтому период 2 л / ® ₀ возмущений смазывающего течения синовиальной жидкости может достигать больших значения, и частоты возмущений в этом случае очень малы.

0,75 [МПа]

1,5 [МПа]

p max =1,777 - 10⁶ Па

C tot =1258,1 Н

/ =0,3 л / « 0 c p max =2,193 - 10⁶ Па

C tot =1612,6 Н

t=n/ «0 c p max=1,786-106 Па

1,5 [МПа]

0,75 [МПа]

C tot =1270,8 Н

t =1,7 n / « ₀ c p _m a _X=1,369 - 10⁶ Па

C tot =909,5 Н

Рис. 8. Распределение давления в зазоре тазобедренного сустава, вызванное вращением сферической головки бедра одновременно в окружном ф -направлении и меридиональном 3 -направлении. Случайные эффекты учитываются, так как р =1/3; вязкоупругость синовиальной жидкости не учитывается, так как р ₀ = 0,00000 Па². Вычисления проведены для ненулевых значений угловых скоростей « 1 =1,40 с ^{- 1} , « ₃= - 0,45 с ^{- 1}, ненулевых значений возмущений угловых скоростей « ₁₀, « ₃₀ при нестационарном течении и для частоты возмущений высоты зазора « ₀=500 с ^{- 1}. R = 0,0265 [м], п = 0 , 15 [ Пас], « ₀ = 500 [ 1/с], « 1 = 1 , 4 [ 1/с], «₃ = 0 , 45 [ 1/с], «_{1 0} = 0 , 1 [ 1/с], «_{3 0} = 0 , 025 [ 1/с], р ₀ = 0, ^=1/3, смазываемая поверхность = 20,38 [cм²]

1,5 [МПа]

0,75 [МПа]

^⁰,3 и / to 0 с , p max =2,407 - 10⁶ Па

Ctot=1792,8 Н t=0, t=2n/to0 с pmax=1,775-106 Па Ctot=1254,7 Н

1,5 [МПа]

0,75 [МПа]

t=n/ too с pmax=1,787.106 Па Ctot=1273,4 Н t=1,7n/w0 с pmax=1,159.106 Па

C tot =726,4 Н

Рис. 9. Распределение давления в зазоре тазобедренного сустава, вызванное вращением сферической головки бедра одновременно в окружном ф-направлении и меридиональном Э-направлении. Случайные эффекты учитываются, так как р = 1/3; вязкоупругость синовиальной жидкости учитывается, так как Po=0,00020 Па2. Вычисления проведены для ненулевых значений угловых скоростей to1 = 1,40 с-1 , to3 = - 0,45 с-1, ненулевых значений возмущений угловых скоростей to10, to30 при нестационарном течении и для частоты возмущений высоты зазора to0 = 500 с-1. R = 0,0265 [м], п = 0,15 [Пас], to0 = 500 [1/с], to1 = 1,4 [1/с], to3 = 0,45 [1/с], to10 = 0,1 [1/с], to30 = 0,025 [1/с], р0 = 0,00020 [Пас2], р = 1/3, смазываемая поверхность = 20,38 [см2]

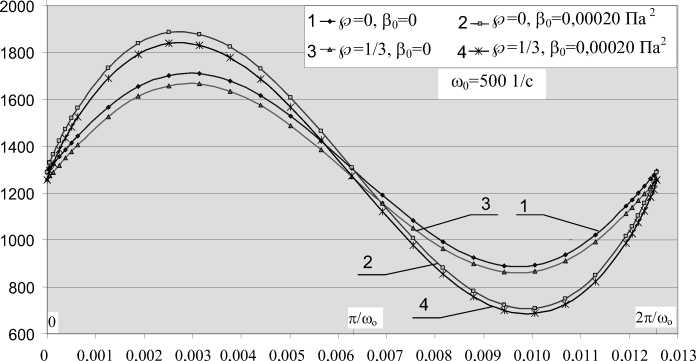
Рис. 10. Зависимость нагрузки от времени за период для четырех предположений, отвечающих следующим случаям: (1) р = 0, р ₀ = 0; (2) р = 0, р ₀ = 0,00020 Па²; (3) р =1/3, Р о = 0; (4) р = 1/3, р ₀= 0,00020 Па²

t , с

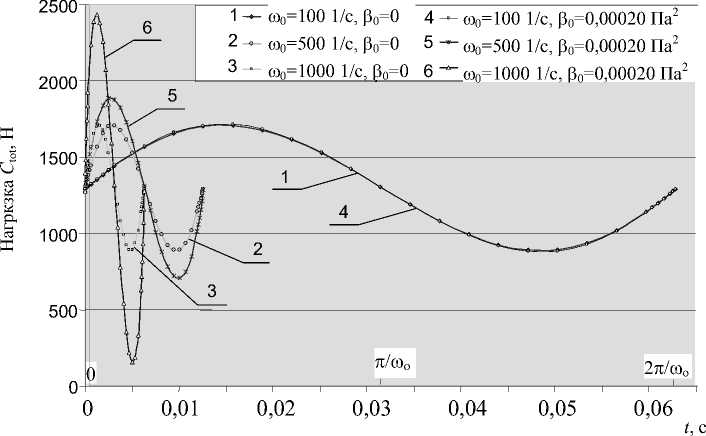
Рис. 11(а). Зависимость нагрузки от времени за период возмущений для двух констант псевдовязкости Р 0 = 0,00000 Па² и р ₀ = 0,00020 Па² и трех различных частот возмущений ю о = 100 с ^{- 1}, ю о = 500 с ^{- 1}, ю о = 1000 с ^{- 1}

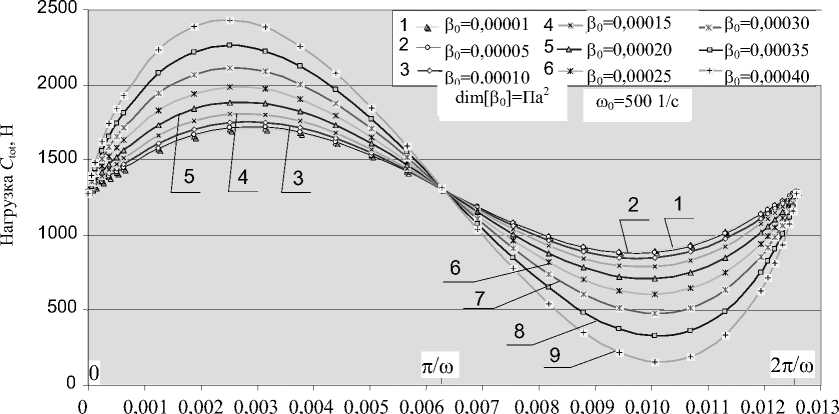
t , c

Рис. 11(b). Зависимость нагрузки от времени за период возмущений при частоте возмущений ю ₀ = 500 с ^{- 1} для различных констант псевдовязкости 0,00001 Па²<  р 0 < 0,00040 Па²

Кривые 1 и 4, приведенные на рис. 11(a), показывают, что для сравнительно малых значений частоты возмущений го ₀ влияние вязкоупругих свойств синовиальной жидкости на суставную нагрузку пренебрежимо мало. Если же частота го ₀ принимает значения от 500 с ^{- 1} до 1000 с ^{- 1}, то вязкоупругие свойства синовиальной жидкости ( р ₀ = 0,00020 Па²) дают увеличение нагрузки в диапазоне от 15% до 60% по сравнению с нагрузкой при р ₀ = 0,0000 Па² (ньютоновская жидкость).

• 8.    Заключение

Полученное уравнение для распределения давления при нестационарных периодических условиях, с учетом случайно меняющегося зазора, вязкоупругих свойств синовиальной жидкости и различных частот и амплитуд колебаний головки бедра и вертлужной впадины приводит, в частном случае, к известной форме уравнения Рейнольдса для стационарного течения.

Из численных расчетов следует, что вязкоупругость синовиальной жидкости приводит к увеличению суставной нагрузки на 15%, а в некоторых случаях на 60%. Влияние вязкоупругости синовиальной жидкости на нагрузку очевидно связано с периодичностью возмущений в суставе. Если частота возмущений больше 100 с ^{- 1}, то вязкоупругость синовиальной жидкости существенно влияет на суставную нагрузку. При частотах, меньших 100 с ^{- 1}, влиянием вязкоупругости на суставную нагрузку можно пренебречь.

Из численных расчетов следует, что стохастическое описание неровностей костных поверхностей и толщины пленки синовиальной жидкости изменяет суставную нагрузку на 11%. Из этих расчетов также следует, что учет смазывания при одновременном вращении головки бедра в двух направлениях позволяет установить точную картину распределения давления в суставе.

Понимание механизма смазывания сустава синовиальной жидкостью с вязкоупругими свойствами весьма важно. Например, такое понимание может существенно улучшить диагностику заболеваний суставов.

Приложение 1

Подставим бесконечные ряды (9) - (12) в систему уравнений (4) - (7) и приравняем члены с одинаковыми верхними индексами в скобках и одинаковыми степенями экспоненциальных функций.

Приравнивая члены с верхним индексом нуль, получим следующие уравнения стационарного движения ньютоновой жидкости:

(A1.1)

5 p ⁽⁰⁾

(A1.2)

(A1.3)

R sin      v ⁽⁰⁾

IR J 8

0,

(A1.4)

д д r

₍  д т ⁽⁰⁾

κ

I ^д r )

+ п

+

(дv. Y

I д r )

(A1.5)

для 0 < ф <  2 п0 1 , 0 < 0 1 < 1, b m = п R /8 < 8 <п R /2 = b s , 0 <  r < s .

Система (A1.1) - (A1.5) определяет искомые давление p ⁽⁰⁾, температуру Т^ ⁰⁾ и компоненты скорости v _ф ⁽⁰⁾, v r ⁽⁰⁾, v ₈ ⁽⁰⁾ по направлениям ф , r , 8 .

Приравнивая члены с верхним индексом к = 1, 2,..., получим следующие уравнения движения для поправок к -го порядка, учитывающих нестационарность течения и вязкоупругие свойства жидкости:

_{( к} )      1        <3)5 p ^{( к} )    5     5 v £ ^к ) )

(A1.6)

(A1.7)

(A1.8)

(A1.9)

I ^{к ю} o P o v ⁽⁾ =^-- cosec I -I — + — П

R V R) 5o   5r V   5r )

₀ = 5 P ⁽ k )

5 r ’

	д p ( к ) I к юоро v ( к ) =--+ 0 0 3        53	5 5 r	< n к V	5 v 3 к ) ) 5 r )	,
5 - 'О * ’ 5ф	D . <3)5 v ( к )    5 + R sin — —r —l-- V R ) 5 r   53	R sin		<3) v к ) " V R 1 3 _		= 0 ,

для к = 1, 2, 3,..., 0 < o <  2 n c 1 , 0 <  c 1 <  1, b m = n R /8 < 3 R/2 = bs, 0 < r < s; n_k = P031+i к®0₽.

Система (A1.5) - (A 1.8) определяет искомые поправки p ^{( к} ) к давлению и поправки v _О ^{( к} ) , v r ^{( к} ) , v ₃ ^{( к} ) к компонентам скорости. Кроме того, получаем уравнение энергии для определения поправок Т^к ) к температуре. Верхние индексы к = 1, 2, 3,... обозначают порядок поправки.

Приложение 2

Проведем преобразование бесконечного ряда периодических функций с известными амплитудами A_imk и известными частотами ю _im в бесконечный ряд с новыми неизвестными амплитудами А*_тк и известной частотой ю ₀ (колебаний в синовиальной жидкости). Это преобразование проводится следующим образом:

у                    у

Е A m ^eX P ( i ^{к ю} 0 t ) = Е ^А тк ^eX P ( i ^к Ю т ¹ ) ,                 ^(A2 .1)

к = 1                               к = 1

где в частном случае i = o , 3 ; т = u , v ; к =1, 2, 3,... и

A * к = U* ,    '. = V* ,   Лик = Uk ,   A* = V» .              (A2.2)

iuk ik ivk ik iuk ik ivk ik

Уравнение (A2.1) описывает следующие случаи:

у                    у                      уу

Е U О к ^eX P ( i ^{к Ю} 0 t ) = Е U О к ^eX P ( i ^{к Ю} О u t ) ,   Е V i ^eX P ( i ^{к Ю} 0 t ) = Е ^V o к ^eX P ( i ^{к Ю} О v t ) ,

(A2.3)

к=1                             к=1                               к=1

у                    у                      уу

Е U*к eXP (iкю0t) = ЕU3к eXP (iкЮ3ut) , Е V3k eXP (iкю0t) = Е V3к eXP (iкЮ3vt) . к =1                             к =1                                к =1

Раскладывая экспоненциальную функцию в обеих частях (A2.1), получим для левой части (A2.1):

Aim 1(1 + i®01 - ^^t)2 — i ^ +) + ....+ 26

^{+ A}im 2 ^{(1 + 2 i} ® 0 ^{1 - 2(} ® 0 ^{1 ) 2} - i         ⁺ ) ⁺ — ^{+             (A2} - ⁴⁾

9(ton1)2 .9(ton1)3.

+ A.. (1 + 3 i to_n 1 —0-^- — i ^{v 0}   + ) + ....

im 3 ^042

Для правой части (A2.1) получаем:

^A im 1^{(1 +} ^ im ¹ - ( ^ im ¹ ^- - i ( ^ im ¹ ^- ⁺ ) ⁺ .... ⁺ 26

^{+ A} im 2 ^{(1 +} ^im ¹ - ^{2( to} im ^{1 ) -} - i     .- ”   ⁺ ) ⁺ .... ^{+             (A-} . ⁵⁾

+ A_{im 3} (1 + 3 ito_z. _mt - ^{9( 4 m 1} ) - i ^ ^ m¹ !- + ) + .... im 3 ' im         4              —                 '

Приравнивая обе части (A2.4) и (A2.5), получим систему линейных алгебраических уравнений:

^Aim 1 ^{+ A} im 2 ^{+ A} im 3 = Aim 1 ⁺ Aim 2 ^{+ A} im 3 ,

A im 1 + 2 A L 2 + 3 A im 3 = ^ m ( A m 1 + 2 A m 2 + 3 A m 3 ),

(A2.6)

(A2.7)

1 *         *      9 *       0 1                    9

2 4m 1 + 24m2 + 4 Am3 = S,I ^ Am 1 + 2 Am2 + 4 Am3), где to

m sim , to0

для i = ф , 9 ; m = и , v .

Решая систему (A2.6), найдем искомые амплитуды:

4 ". 1 = J A m 1 (2 - S ,„ )(3 + 2 S m ) + 2 A m 2 (1 - S m )(3 + 4 S ,„ ) + 3 A . , (1 - S ,„ )(2 + 3 S ,m ),

A m 2 = J A m 1 (1 - S m )(3 - 4 S „ ) + 5 A m 2 (1 - 2 S „ )(3 - 8 S „ ) + 5 A m 3 (1 - S „ )(1 - 6 S „ ), (A2.8)

a,".,3 = - 2 Am 1(1 - Sm )(2 - S m ) - 5 Am 2 (1 - 2Sm )(1 - Sm ) - J Ams(4 - 1 8S m + 9Sim,), где i = ф, 9; m = u, v. Например, символ A*imk для k = 1, 2, 3,^ описывает следующие амплитуды:

ii ф u 1    ^ ф1 ,

Л *   = U *  = if

Л фи 2    <-Уф2,   ^ф и 3    <-Уф3, ii

9 и 1         9 1 ,

л * =и* i =тг

9 и 2    ^9 2 ,    ^9 и 3    ^9 3

ii

²¹ф v 1    ^г ф1 ,

ii ф v 2 г ф 2 ,

ii ф v 3 ^г ф3 ,

(A2.9)

ii

9 v 1        9 1 ,

ii 9 v 2     ^г 9 2 ,

ii

²¹9 v 3     ^г9 3 ,....

Из (11) и (A2.2) для i = ф , 9 ; m = и , v следует:

А 21ф и 1	= U ф1	_ и фД 15 ,	А ф и 2	= U ф 2	= Ц р^ 25	,    A ф и 3	> = U Ф 3 =	U фД 3 5 ,
A 9 и 1	= U 9 !	_ U 9^ 15 ’	А 9 и 2	= U 9 2	= и ^д 25	А =Т1 = , ^9 и 3    ^ 9 3		U 9Д 35
A ф , 1	= Vv	Vф о = ^Г,	A ф , 2 =	V , 2 =	V ф о 25 ,	A ф , 3 =	V _°^ ф 3    35	,.....
A 9 , 1	= V »r	=V o 1 5 ,	A 9 , 2 =	: V 9 2 =	V 9 о 25 ,	A 9 , 3 =	V = V 9 3 9 3    35	,....

(A2.10)

Например, амплитуды колебаний в окружном ф и меридиональном 9 -направлениях имеют следующий вид:

Ц = 5 U , 1 (2 - s и )(3 + 2 s „ ) + 1 U , , (1 - s „ )(3 + 4 s „ ) + 1 U „(1 - s „ )(2 + 3 s . ), U i\ = 5 U , 1 (1 - s u )(3 - 4 s u ) + 5 U„(1 - 2 s u )(3 - 8 s „ ) + 5 U , 3 (1 - s и )(1 - 6 s „ ), (A2.11) U i * = - § U , 1 (1 - s u )(2 - s u ) - у U , ₂(1 - 2 s u )(1 - s u ) - 5 u, 3 (4 - 18 s u + 9 s , 2 ),

V * = 5 V 1 (2 - s , )(3 + 2 s „ ) + 2 V 2 (1 - s v ) (3 + 4 s v ) + 5 V 3 (1 - s , )(2 + 3 s „ ),

V * = 5 V , . (1 - s , )(3 - 4 s , ) + 5 V 2 (1 - 2 s , )(3 - 8 s ,, ) + 3 V 3 (1 - s v, )(1 - 6 s , ),

V * = - 2 V ,(1 - sv )(2 - s ,) - 4 V 2(1 - 2 s , )(1 - s ,) - 5 V 3(4 -18 s , + 9 s,v), где г = ф, 9. Используя (A2.10)-(A2.11), найдем:

и *k =    Sm , V = V S ,,k ■                    (A2.12)

k          k для г = ф, 9 и k = 1, 2, 3,..., где:

S m 1 /1⁵ = 2 (2 - s m )(3 + 2 s m ) + A1 - s m )(3 + 4 s m ) + 1(1 - s m )(2 + 3 s m ) , о

2'

S m 2

/ 2⁵ = 1(1 - s m )(3 - 4 s m ) + 1(1 - 2 s m )(3 - 8 s m ) + 2(1 - s m )(1 - 6 s m ) , о

(A2.13)

S m ^: = 5

-2(1 - s m )(2 - sm) - 1(1 - 2sm )(1 - sm) - 1 (4 -18s m + 9s,m) , где m = и, , и i = ф, 9. Для го,m = го0 получим sm = 1 .Следовательно, Smk= 1 для m = u, , и Uk* = U., Vk* = V,k. Из медицинских экспериментов известно, что 0,95

+0,964 < <+1,034, + 0,016 < m²^<+0,048, - 0,006 < m³^<+0,021,... (A2.13)* ^, 15 j j j 25 ^{J J J} 35 j j x /

Применяя аналогичный алгоритм вычислений для температуры (14)2 и для выражения (22), получим решение, аналогичное (A2.8). Искомые амплитуды для компоненты скорости в направлении высоты зазора имеют вид:

W." = 5 W(2 - Sr )(3 + 2 s,) +1 W₂(1 - s, )(3 + 4 s,) +1 W3(1 - s, )(2 + 3 s,),

W2 = 5 W(1 - Sr)(3 - 4S_r) + 5 W2(1 - 2Sr)(3 - 8Sr) + 5 W3(1 - s,)(1 — 6Sr),     (A2.14)

W =-5 W(1 - Sr )(2 - Sr) - 5 W2(1 - 2 s,)(1 - Sr) - 5 W3(4 -18 Sr + 9 Sr), где

Sr ^.                         (A2.15)

®0

Учитывая, что £^(k) = Be£⁽⁰⁾/k⁵, находим из (23):

W1 £ ' гоr = Be£ гоr, W2 = 2s⁽²⁾tor = 2Be£⁽⁰⁾tor / 2⁵=    Be8⁽⁰⁾tor,

²            (A2.16)

W3 = 3£⁽³⁾tor = 3Beгоr/3⁵= уB£ гоr...... Wk =   Be£⁽⁰⁾™r.

Тогда из (A2.12) - (A2.14) следует, что to £(0) В                 to £(0) В                   to f(0) В

* to°^£Be          .   to°^£Be            . Ю0£ Be

(A2.17)

1           4      ^r 1, ^vv=         ^4     °r 2’...,^ ^vk         ,4     °rk ,

12  k где

Sr 1/1⁴

= 1 (2 - Sr )(3 + 2 Sr) + |_г(1 - Sr )(3 + 4 Sr) + ^(1 - Sr )(2 + 3 S) , о

Sr 2/2⁴

Sr 3/3⁴

2'

3'

= 1 (1 - Sr )(3 -4Sr)+1x1 - 2Sr )(3 -8Sr)+|_r(1 - Sr )(1 -6Sr) , о

-2(1 - Sr )(2 - Sr) -1(1 - 2Sr )(1 - Sr) -1 (4 -18Sr + 9S,²) .

(A2.18)

__*     __

Wk = Wk и

Для го_r = too находим S_r = 1 и, следовательно, S_rk = 1. В этом случае Tk.

T_k*=

Теперь выведем выражение для высоты гладкого зазора £⁽⁰⁾. Соотношения между прямоугольными (x, у, z) и сферическими (ф, r, У) координатами (см. рис. 3)

имеют вид:

x = r 81п(Э1)со8ф, y = r 81п(Э1)81иф, z = r cos(3i), 0 <r<R, Э1=Э/R.      (A2.19)

Графически положения центра сферической головки бедра O(0, 0, 0) и центра сферической вертлужной впадины 0₁(x-Д£₁, y-А£₂, z+А£₃) показаны на рис. 3. Уравнение поверхности сферической вертлужной впадины в окрестности центра 0₁(x-Д£₁, у-А£₂, z+Д£₃) можно записать в виде:

• (x-А£1)²+ (у-А£2)²+ (z+А£3)²=(R+D+£ mm)², D = [ (А£1)²+(А£2)²+(А£3)²]^0,5.    (A2.20)

Подставляя (A2.19) в (A2.20), получим:

• (r со8ф sin9₁-А£₁)²+(r 81пф 81п9₁-А£₂)²+(r СО8$₁+А£₃)²=(R+D+£_min)².    (A2.21)

Высота зазора

£⁽⁰⁾(ф.9₁) - r -R.

(A2.22)

Найдем r из (A2.21) и подставим эту величину (A2.22). Тогда получим окончательное выражение для высоты зазора в виде (22).

Приложение 3

Предположим, что динамическая вязкость синовиальной жидкости не меняется в направлении высоты зазора. Интегрируя (A1.1) и (A1.3) дважды по переменной r1 и учитывая граничные условия (16), (18), получим компоненты скорости синовиальной жидкости в окружном и меридиональном направлениях в виде:

1    1       <9^5p⁽⁰⁾ .

vф = ^-7-----cosec          ^{£ 5 (1}- ⁵) + Uф0⁽¹- ^5),           (A³-¹)

2n0n1 R     IR /оф v^ =- ----£2 5 (1 - 5) + U»o(1 - 5 ),                (A3.2)

2ПоП1 d9

где 5 - r/s. 0 < r. 0 < ф < 2п6₁. 0 < 0₁< 1, пR/8 < 9 < пR/2.

Интегрируя (A1.6), (A1.8) дважды по переменной r1 и учитывая граничные условия (19), получим поправки к вышеуказанным компонентам скорости, вызванные нестационарностью течения и вязкоупругими свойствами жидкости [3]:

„(k) -n V +n* sinhK^6-r)Ak] + г* sinh^(rAk) v = ⁿikYk⁺Uik      - ,             ⁺Vik - , x ,

(A3.3)

(A3.4)

(A3.5)

sinh ( £A_k)         sinh ( £A_k)

Yk-[I - exp (rAk)]-[! - exp (£Ak)] sinhirAkl, П.-i, n„=dpi A - kro0p0R sin(9 / R) 5ф           kro0p0 59             nk где k = 1. 2. 3..... при i = ф. 9. 0 < ф < 2л61, 0 < 61 < 1. пR/8 < 9 < пR/2. 0 < r

Приложение 4

Интегрируем уравнение непрерывности (A1.4) по переменной r1 с учетом граничных условий (17). Компонента скорости синовиальной жидкости в направлении высоты зазора принимает тогда следующий вид:

v <°) =

r

--cosec

R

^ф dr - cosec 5ф

-9Yf — RJo d9

v 9⁰⁾

dr.

(A4.1)

Интегрируем уравнение непрерывности (A1.9) по переменной r1 с учетом граничных условий (20)1. Тогда поправки к вышеупомянутой компоненте скорости, вызванные нестационарностью течения и вязкоупругими свойствами жидкости, принимают вид:

(k) r

--cosec

R

5v⁽k)

^ф dr - cosec 5ф

-Tr—

R^Jj 59

v<*)sin f-)

⁹v R J

dr,

(A4.2)

где k = 1, 2, 3,..., 0 < ф < 2л9_ь0 < 61 < 1, nR/8 < 9 < nR/2, 0 < r< s.

Учитывая граничное условие (18) для i = r на компоненту (A4.1), найдем:

r 5v^{(0)        s}5

_v9(0)

dr = 0.

(A4.3)

f ф dr + Rf—

^Jo 5ф       J 59

Учитывая граничное условие (23) на компоненту (A4.2), найдем:

^r5 v^(k) ^ra f -d-d.r + Rf— 0 5ф 0 59

_v9(k)

*

dr = - i W R sin — ^kVR

(A4.4)

0 < ф < 2n61, 0 < 61 < 1, nR/8 < 9 < nR/2, 0 < r < s.

Приложение 5

Подставим компоненты скорости (A3.1), (A3.2) в (A4.3). Тогда получим модифицированное уравнение Рейнольдса (26). Используя правило дифференцирования интеграла с переменными пределами и граничное условие (21)1, найдем из (A4.4):

5 r _(k) , _n 5 r _(k) . f 9) , .„.._n . f9) _.* 5s _nT.« . f9)5s _ .. — v,(,^k) dr + R— v^(k )sin — dr = -i W. R sin — + V,— + RV„sin — — . (A5.1) 5ф ^J₀^ф59 ^J₀⁹V R J k V R J ^фk 5ф ⁹k V R J 59

Подставив в (A5.1) поправки к компонентам скорости (A3.3) для i =ф, 9, найдем:

5ф

5 ⁺^* ⁵Ф

5 +

cosec R

^(k) г

'"   I Ykdr

⁵Ф ^j

^k Ю0Р0

+ R A

5p^(k) .

sin

+

U, S-^{sinh [(s - r})Ak^]_dr + V* г sinh⁽rAk) _dr ^фk^{j   sinh}[^sAk ]         ^фk^jsinh(^sAk )

kto_oPo _D ■

^{0 0}Rsin

f 9)

= - k ro„p„ W, R sin — +

00 k

V R J

U* r^sinh[^{(s - r})Ak ] ^{9k j   sinh}[^sAk ]

k Ю0Р0

^ +

„ r sinh (rA_k) dir + V_9k ---^4+г

j sinh [s Ak ]

* 5s    _nT_* 5s . f 9

V—+ RVik—sin — ^фk 5ф       ^9k 59    (7?

,

(A5.2)

для k = 1, 2, 3,..., 0 < ф < 2n61, 0 < 61 < 1, nR/8 < 9 < nR/2, 0 < r< s.

Для дальнейшего упрощения (A5.2) необходимо вычислить следующие интегралы:

^kЮ0Р0U* f^{sinh [( s - r})Ak^]_dr = i ik^{j   sinh}[^sAk ]

k Ю0Р0

£

U'-k j

e(s-r)Ak - e-(s-r)Ak s AL     -s AL e k - e k

dr

^k Ю0Р0 i Ak

U_i^*_k tanh

2 i k to0^p0U-k

s - — s³A2 + Ofs⁴]

12 ^k

, при i = ф, 9.

(A5.3)

J Ykdr = J (1 - erA

)-(1 - e^sAk

erAk — e - rAk ) e=Ak — e -=Ak

dr =

s +--tanh Ak

i s³

— — ^ktooPo ^-О(^s) , ¹²nk            ^v ’

(A5.4)

V* кЮ0Р0s ^{sinh r}Ak dr = ^ik i ^Jsinh s Ak

*

Vik

ktoA

£

J

e^rAk - e-^rAk e⁶Ak - eAk

dr

= - 2 iktooPoV

s-—s3 Ak2 + O (s4)

12 ^k

(A5.5)

для i = ф, 9.

Подставляя (A5.3), (A5.4), (A5.5) в (A5.2), получим модифицированное уравнение Рейнольдса для поправок к давлению:

1     <9^ 5

— cosec I — I— R     v R J 5ф

.            ( 9

= 12i W_r R sin — ^k IR

s³5p^(k)

П k 5ф

-12

+ R А

V • — +

фk 5ф

+6 [Uф k (⁹)+Vk ]

8    .

sin n k

5p^(k)

„ . p) 5s

RV sin

^9k       J 59

58- p p< sLЛ 5ф 12 5ф(пkJ

i^ktooPo

+

+

(A5.6)

+6 R [U9,(ф)+у;, ]•

s sin

1 512 59

s sin

nk

i^ktooPo >.

для k = 1, 2, 3,..., 0 < ф < 2л61, 0 < 61 < 1, nR/8 < 9 R/2, 0 < r< s.

Благодарность

Данный исследовательский проект был поддержан Ассоциацией по передаче знаний им. Марии Кюри в рамках Шестой Программы Европейского Сообщества; номер контракта – MTKD-CT-517226.