Нейронечеткие модели в задачах извлечения правил из искусственных нейронных сетей

Averkin A. N., Lishilin M. V. Neuro-fuzzy models in problems of extracting rules from artificial neural networks. System Analysis in Science and Education, 2021;(3):30–43(In Russ). Available from:

Масштабное развитие систем искусственного интеллекта (ИИ), в том числе приложений на основе искусственных нейронных сетей, открывает широчайшие возможности их использования в различных областях, от систем распознавания эмоций, до систем предиктивной аналитики, применения в медицине и военной области. Но, в то же время, существующие системы и приложения имеют один общий существенный недостаток – невозможность интерпретации полученных результатов и принятых решений. Широко известная проблема так называемого черного ящика накладывает существенные ограничения для использования подобных систем, в том числе законодательных, так как нельзя проследить ход принятия решения нейронной сетью.

В настоящее время эти проблемы решаются в рамках направления объяснимого ИИ ( explainable artificial intelligence или XAI ). Системы на базе объяснимого ИИ помогают понять пользователю принятые с помощью методов машинного обучения решения, что повышает доверие к этим системам и дает возможности принимать более эффективные решения на основе результатов работы системы. Все это позволяет разработчикам и пользователям исследовать факторы, которые используются нейронной сетью при решении конкретной задачи и понять, какие параметры нейронной сети нужно поменять, чтобы повысить точность ее работы.

Применение методов нечеткого интеллектуального управления для создания систем управления на примере управления моделью трактора

В рамках работ по реализации гранта Правительства Московской области на тему «раз-работка и создание программно-аппаратного комплекса (ПАК) для автоматического беспилотного управления сельскохозяйственной техникой при возделывании земельных участков Московской области с реализацией облачных сервисов построения маршрутов на трехмерной модели поверхности и удалённым мониторингом оператора на основе технологий VR / AR » в государственном университете «Дубна» была предложена нечеткая семиотическая система управления трактором на базе нечеткого одношагового контроллера, обходящаяся возможным наименьшим количеством продукционных правил.

Данная модель создавалась для обеспечения автономного режима управления трактором по заданным параметрам с перехватом управления удаленным оператором в случае нештатной ситуации. Ниже приведено описание созданной модели и некоторых теоретических положений, положенных в основу ее создания.

Для программирования модели разрешено использовать только условия. Использование любых сравнений запрещено.

Трактор имеет следующие сенсоры:

• 1.    Сенсор прямого препятствия Dfront .

• 2.  Парные сенсоры боковых препятствий DL 90, DR 90 расположенные под углом 90 ° от Dfront .

• 3.  Парные сенсоры боковых препятствий DL 30, DR 30 расположенные под углом 30 ° от Dfront .

• 4.  Парные сенсоры цели DLGold, DRgold расположенные под углом 3 ° от Dfront .

• 5.  Показатель скорости Dsp .

• 6.  Сумматор скорости DspSum .

• 7.  Сумматор циклов измененной модели DChMod .

• 8.  Сумматор сенсоров.

Сенсоры внешнего мира трактора моделируют действия лазерного дальномера лидара, который выпускает несколько лазерных лучей в разных направлениях для оценки расстояний от трактора до препятствий или виртуальных линий разметки (элементов дополненной реальности).

Задача трактора – движение по заданной траектории с обходом препятствий и движение к целевой позиции на поле цели в рамках заданных ограничений. Для простоты далее будем использовать прямоугольный тип препятствия, хотя полученная система управления может работать в лабиринте с произвольным видом препятствий.

Для начала введем понятие точки поля. Назовем точкой поля самый минимальный по размеру элемент метрического пространства, который может находиться в одном их трех состояний: «ПУСТО», «ПРЕПЯТСТВИЕ», «ЦЕЛЬ». Далее введем понятие кластера. Кластер – это замкнутая область точек, находящихся в одном из трех вышеперечисленных состоянии. Теперь можем определить понятие лабиринта. Под полем будем подразумевать замкнутое метрическое подпространство, в которое входят произвольное количество кластеров типа «ПУСТО» и «ПРЕПЯТСТВИЕ» и один кластер типа «ЦЕЛЬ». Все предельные точки лабиринта находятся в состоянии «ПРЕПЯТСТВИЕ».

Трактор (робот) в данной задаче является автономным транспортным средством. На борту находится двигатель, который вращает задние колеса трактор. Двигатель может находиться в одном из трех состояний: «Ускорение», «Торможение» и «Отключен» или в численном выражении +1, -1 и 0. Трактор может поворачиваться вокруг своей оси при помощи руля, двигающего передние колеса робота. Руль также может находиться в одном из трех состояний: «Направо», «Налево», «Нет поворота». В отличие от логического типа состояния двигателя, руль имеет количественные показания – угол поворота.

Трактор на своем борту имеет сенсоры для считывания информации с внешнего мира или состояния трактора. Сенсоры можно разделить на три вида: сенсор – датчик непосредственного считывания информации с внешнего мира. Показатель – датчик считывания информации с внутренней системы трактора. Сумматор – этот датчик возвращает свое максимальное значение, а при некотором условии он обнуляется и начинает возвращать в систему сумму некоторого показателя, до наступления другого условия, когда сумматор будет опять возвращать максимальное значение.

Для управления трактором было предложено три модели: модель объезда трактором препятствий, модель выхода из тупиков, модель приближения трактора к цели.

Модель объезда трактором препятствий предназначена только для объезда роботом препятствий. Логика работы трактора состоит в том, чтобы он перед препятствием уменьшал скорость и поворачивал от него. На рисунке 1 представлена типичная ситуация, с которой может столкнуться трактор при движении на пространстве с препятствиями.

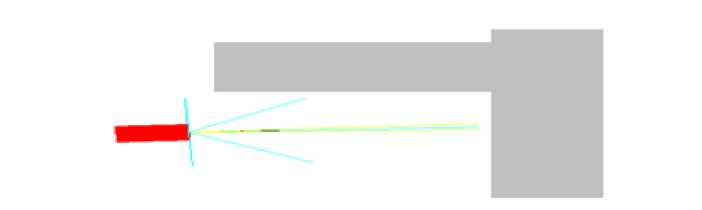
Рис 1. Типичная ситуация подхода трактора к препятствию

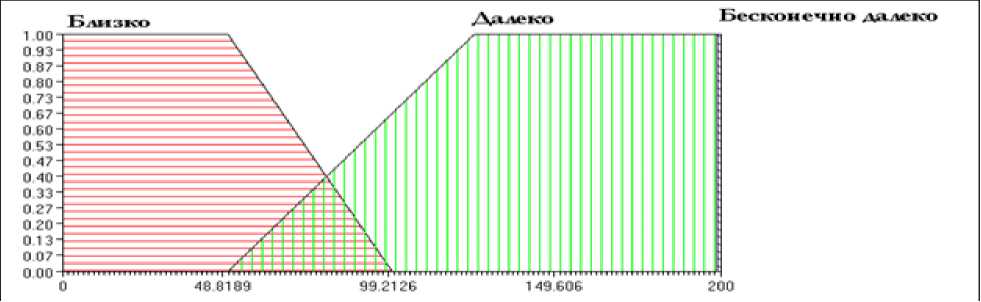
Рис 2а. Функции принадлежности переменной «Расстояние» для Dfront

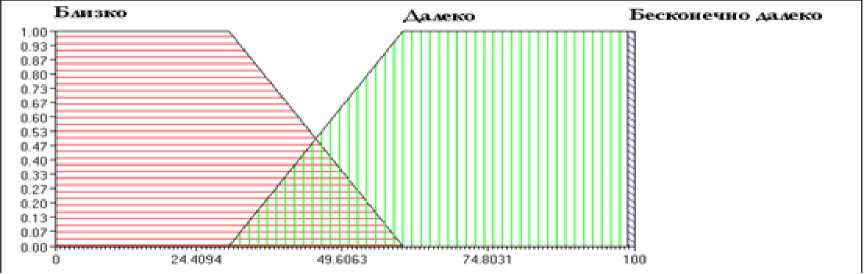
Рис 2б. Функции принадлежности переменной «Расстояние» для DR90 и DL90

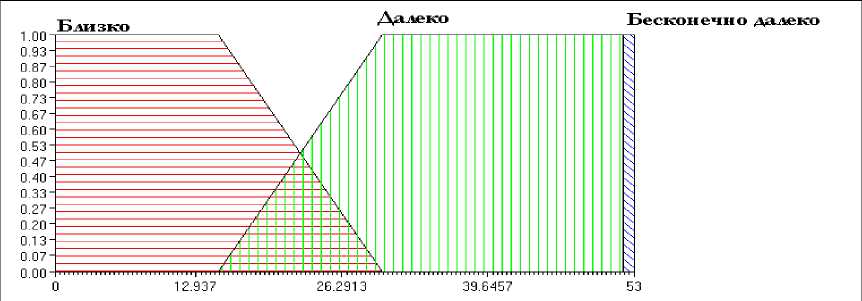
Рис 2в. Функции принадлежности переменной «Расстояние» для DR30 и DL30

На рисунке 2 а, б, в представлены функции принадлежности внешних сенсоров. Кратко правила для данной модели можно охарактеризовать так: нечеткий регулятор имеет дело с одной лингвистической переменной – «расстояние», которая может принимать три значения: «близко» (« Close »), «далеко» (« Far ») и «бесконечно далеко» (« Infinity »). Эти значения имеют одинаковые функции принадлежности для симметричных датчиков, но разные для других. То есть боковые сенсоры DL 90, DR 90 (« LSEye » и « RSEye ») имеют одинаковые функции принадлежности, тогда как сенсоры DL 30, DR 30 («LefEye» и « RigEye ») имеют уже другие функции. Датчик прямого препятствия Dfron t (« MidEye ») влияет на выходное значение лингвистической переменной «ускорение»: если робот фиксирует перед собой препятствие, он делает торможение, в противном случае он ускоряет свой ход. Ускорение может принимать три значения (три состояния двигателя) «нулевое» («Zero»), «ускорение» (« SpeedUp ») и «торможение» (« Braking ») (см. рис. 3).

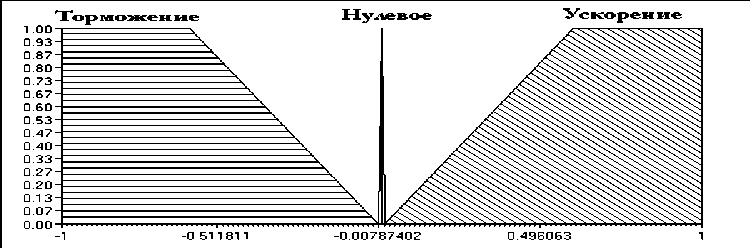
Рис 3. Функции принадлежности переменной «Ускорение»

Для правильного функционирования модели робот имеет датчик измерения скорости Dsp (« Speed ») (см. рис. 4). Лингвистическая переменная «Скорость» имеет следующие значения: «нулевая» (« Zero »), «маленькая» (« Small »), «средняя» (« Middle »), «быстрая» (« Fast »), «сумасшедшая» (« Crazy fast »).

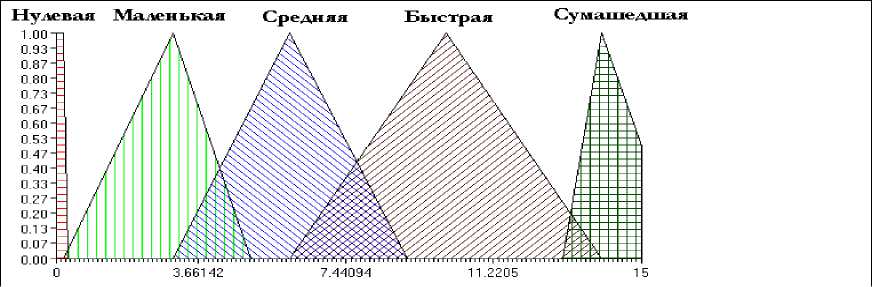
Рис 4. Функции принадлежности переменной «Скорость» для DSp

Сенсоры бокового зрения меняют выходное значение лингвистической переменной «Поворот» (см. рис 5). «Поворот» может иметь значение «нет поворота» (« No turn »), «направо» (« Right turn ») и «налево» (« Left turn »). Для вычисления вектора поворота робота проверяются парные боковые сенсоры и поворачивает в ту сторону, где дальность до препятствия больше. Если робот фиксирует препятствия, то сенсоры расстояний дают значение «бесконечно далеко».

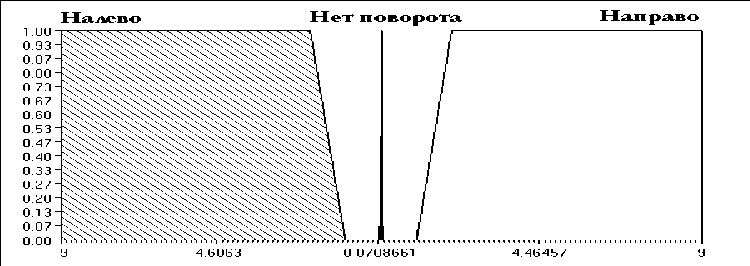
Рис 5. Функции принадлежности переменной «Поворот»

Данная модель (назовем ее модель объезда препятствий) позволяет роботу эффективно объезжать препятствия. Однако проведенные эксперименты показали, что в некоторых областях лабиринта робот «застревает». Это значит, что робот перед препятствием имеет нечеткую нулевую скорость и нечеткий нулевой вектор поворота.

Для описания модели выхода робота из тупиков введем некоторые определения.

О п р е д е л е н и е 2. 1. Областью четкой неопределенности называется область лабиринта, находясь в которых на парные сенсоры робота подается тождественно равный сигнал.

О п р е д е л е н и е 2. 2. Областью нечеткой неопределенности называется область лабиринта, находясь в которых парные сенсоры робота возвращают одно и тоже значение лингвистической переменной «расстояние».

О п р е д е л е н и е 2. 3. Компенсационным эффектом называется ситуация, когда на разнопарные сенсоры и сенсор прямого видения приходит информация о препятствиях, а на остальных двух сенсорах препятствия не фиксируются (« Infinity »)

Теперь посмотрим на правила. В списке правил не существует правила типа:

IF D1 IS Value 1 AND D 2 IS Value 1 THEN Rotate IS Value 2, где D 1 и D 2 – разносторонние боковые сенсоры, Value 1 – некоторое значение переменной «Расстояние», кроме « Infinity », Value 2 – некоторое значение переменной «Поворот». Это правило не введено специально, потому что, имея одинаковые данные с сенсоров, невозможно найти вектор поворота.

Вследствие этого определения, робот, попадая в область нечеткой неопределенности, не может определить, куда ему двигаться, потому что в правилах не определено, как двигаться в подобных случаях. Следующий рисунок 6 иллюстрирует данный процесс.

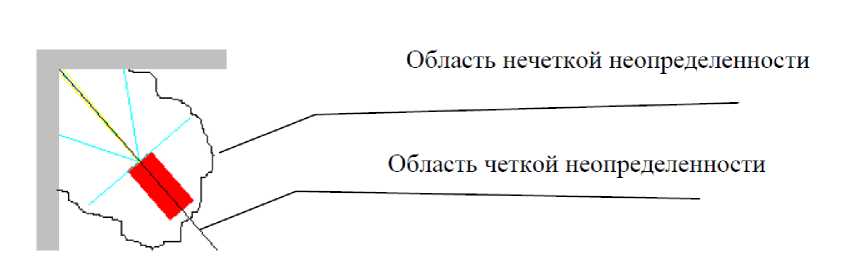
Рис 6. Нечеткая неопределенность

На рисунке видно, что на боковые сенсоры DR 90 и DL 90 приходит информация, что препятствие не определенно (« Infinity »), а на другие сенсоры DR 30 и D L30, что препятствие далеко (« Far »). Робот, в соответствии с правилами, приблизится к препятствию, но обойти не сможет, поскольку на сенсоры поступает однородная информация.

Рассмотрим теперь компенсационный эффект. Пусть робот попал в ситуацию, показанную на рисунке 7.

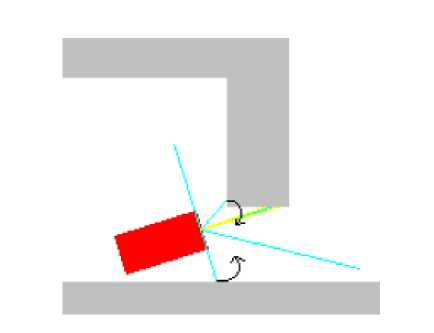
Рис 7. Компенсационный эффект

Как мы видим, два сенсора и сенсор прямого видения фиксируют препятствие, а два других нет. Нечеткий регулятор (используя соответствующие правила) пытается сместить вектор движения

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №3, 2021 год трактора (на рисунке обозначено стрелками) в разные стороны. В результате вектор поворота равен нулю.

Использование опыта в данной модели невозможно, поскольку у робота отсутствует память и механизмы вывода знаний из данных ( data mining ). Кроме того, даже если возможность накапливания знаний была бы реализована, все равно если бы трактор впервые попал бы в область нечеткой неопределенности или в область компенсационного эффекта, то он не смог бы выйти, поскольку опыта у него нет. Далее, рассмотрим частный случай стохастического метода – правило типа:

IF D 1 IS Value 1 AND D 2 IS Value 1 THEN Rotate IS Value 2, где D 1 и D 2 – парные боковые сенсоры, Value 1 – некоторое значение переменной «Расстояние», кроме « Infinity », Value 2 – некоторое значение переменной «Поворот», например, « LeftTurn » или « RightTurn ». Но метод позволяет трактору выйти только из половины всех возможных тупиков. Нам остается использовать только метод повышения точности сенсора. Именно этот метод будет описан далее. Однако одношаговый контроллер не может сам повысить точность сенсоров. Для этого мы вводим новую модель, предназначенную исключительно для выхода трактора из тупика и мета-уровень переключающий модели в нужный момент.

Для того чтобы определить момент переключения между моделями должен быть выработан критерий попадания робота в тупик. У трактора есть внутренний сумматор – «Сумма скорости», DSpSum (« SpeedSum »). Этот сумматор действует следующим образом. Он все время возвращает в систему максимальное свое значение, в то время как внутри себя он реально суммирует скорость, но по прошествию определенного количества циклов возвращает реальное значение суммы скорости робота. Теперь критерий попадания трактора в тупик будет следующим: если значение датчика суммы скорости упало до какого-то предельного значения SpSum > 0, то трактор попал в тупик. То есть DSpSum <  SpSum . В этот момент мета-уровень меняет модель объезда препятствий на модель выхода из тупиков следующим образом: проводим не полное монотонное преобразование с сенсором DL 30 при коэффициенте неоднородности равном 1. То есть этот сенсор остается неизменным, а остальные сенсоры бокового зрения уменьшают свою «видимость», сжимая функции принадлежности переменной «Расстояние» (увеличивая тем самым чувствительность сенсора), до минимального значения некоторого τ min ≠0 (рис. 8). Стрелка на рисунке показывает направление поворота робота. Результатом изменения модели является то, что теперь с датчиков снимается неоднородная информация (все сенсоры, кроме одного показывают значение «Бесконечно далеко» (« Infinity» ), а один датчик возвращает истинное значение до препятствия) и робот (в соответствии с правилами) может найти выход из тупика. Хочу обратить внимание, что τ min обязательно должно быть не нулевой величиной. В противном случае робот, выполняя поворот в узких тупиках, будет ударяться о стенку.

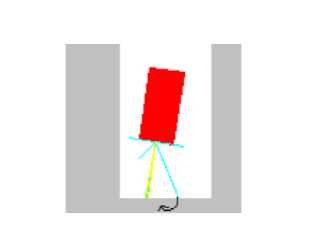
Рис 8. Выезд из тупика

Итак, изменение модели сводится к тому, что мета-уровень изменяет «видимость» (то есть дальность определения сенсора цели) сенсора, при этом в правила вывода предыдущей модели принципиальные изменения не вносятся.

После того как датчик суммы скорости вышел за пределы SpSum (то есть DSpSum >  SpSum ), для мета-уровня это является сигналом к переключению на исходную модель объезда препятствий.

Рассмотрим случай: пусть трактор попал в тупик. Он изменил модель и начал поворот. Если не существует препятствия, которое находится в той стороне, куда робот поворачивает, то робот обязательно выйдет из данного тупика, поскольку на поворот влияет только один сенсор. Теперь пусть там будет стоять препятствие. Трактор опять застрянет, поскольку один из уменьшенных сен- соров коснется препятствия и возникнет эффект компенсации. На рисунке 9 показан эффект компенсации во время измененной модели выхода из тупика.

Рис 9. Стрелкой на рисунке показано направление поворота

Из примера видно, что данная модель дает решение не во всех случаях. Для того чтобы система всегда выходила из тупиков, необходимо активировать в системе еще один датчик – «счетчик циклов измененной модели», DChMod (« CyclesChModel »). Он действует следующим образом: пока действует модель объезда препятствий, датчик возвращает в систему свое максимальное значение. Как только начинает действовать модель выхода из тупика, счетчик обнуляется и возвращает значение, которое увеличивается каждый цикл действия нечеткого регулятора. Если достигнут критерий выхода из тупика DSpSum >  SpSum , то мета-система возвращается к модели объезда препятствий, а датчик опять начинает возвра-щать свое максимальное значение. В противном случае, если датчик циклов достиг некоторого , а датчик суммы скорости не переходит значения SpSum , то можно сказать, что система опять попала в тупик и необходимо изменить вектор поворота системы. Этот критерий можно записать так: DChMod> а & D spSum > SpSum .

Для того чтобы гарантировать выход из тупиков мы должны изменить алгоритм выхода следующим образом:

• 1.    Пронумеруем произвольным образом сенсоры датчики.

• 2.  Обнуляем сумматор сенсоров.

• 3.  Увеличиваем на единицу сумматор сенсоров.

• 4.    Проводим не полное монотонное преобразование сенсором номер которого находится в сумматоре сенсоров.

• 5.    Если, за время действия сумматора циклов измененной модели, был достигнут критерий выхода из тупика, то меняем модель на модель объезда препятствий.

• 6.    Если сумматор циклов вышел за пределы лимита, переходим на шаг 3.

Данное изменение гарантирует выход из тупика в статических лабиринтах и с положительной вероятностью выход их динамических лабиринтах, речь о которых пойдет ниже.

Датчик «счетчик циклов» имеет аналог в реальных моделях, используемых живыми существами. Как правило, системы с такими датчиками используют оппозиционные лингвистические шкалы, где на разных концах стоят пары антонимов. В данном случае «Не очень долго» и «Долго».

В нашей системе априори задается прогнозируемое время, когда необходимо изменить вектор поворота. Это значение и есть а.

Итак, после дополнения в систему модели выхода из тупика и мета системы робот стал уверенно выходить из всех областей нечеткой неопределенности, тупиков, а эффект компенсации больше не мешал движению робота. Это подтвердили многочисленные эксперименты.

Теперь для решения глобальной задачи поиска цели, необходимо задействовать сенсоры, регистрирующие цель - DL, DR. Они расположены под углом 3° от датчика прямого препятствия Dfront и имеют одни и те же функции принадлежности, что и DL90, DR90, однако регистрируют только цель. Если хотя бы один из «золотых» датчиков «почувствовал» цель, то трактор немного поворачивается в сторону, чтобы цель могли регистрировать оба датчика, а не один, это нам должно, гарантировать, робот дойдет до золота под нужным нам углом (рис. 10). Это достигается дополнением лингвистической переменной «Поворот» значениями «Немного вправо» и «Немного влево» и соответствующими правилами вывода (рис. 11). Как только два «золотых» датчика начинают регистрировать цель, автоматически датчик Dfront, также попадая на цель, согласно правилам, начинает тормозить робота, обеспечивая плавный подход к цели.

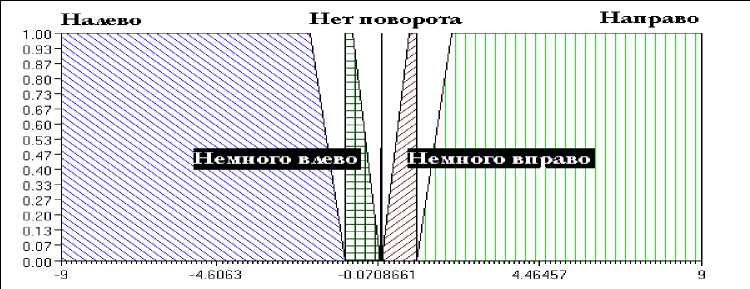
Рис 10. Добавленные значения переменной «Поворот»

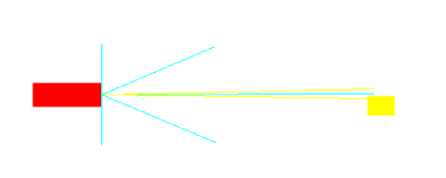
Рис 11. Трактор «коснулся» одним датчиком цели

Данная модель хорошо работает в пустых полях, то есть, когда рядом с целью нет никаких препятствий. Эксперименты показали, что, стоит только добавить небольшую стенку так чтобы хотя бы один их датчиков касался ее, то робот отходит от цели, поскольку этот датчик повернет трактор от препятствия, т.к. любое значение «Немного вправо» или «Немного влево» меньше чем просто «Вправо» или просто «Влево».

Для того, чтобы показания боковых счетчиков не влияли на достижения трактором цели, в мета систему вносится некоторый параметр п, который в системе изменяет показания боковых датчиков следующим образом:

f D ,, еслиD_i <  п

• D = 1 i ^,

[ 0, еслuD_i > п

, где D i – i -й боковой датчик.

Таким образом, данное изменение позволяет трактору успешно находить цель в лабиринте. При этом мета система может переключать модели следующим образом (см. рис. 12). Принципиальная конечная схема действий трактора показана на рис. 13.

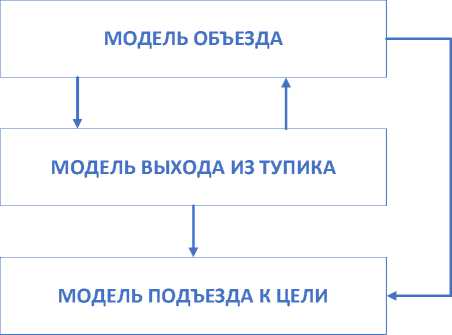
Рис 12. Схема переключения модели

Стрелками на схеме обозначена возможность перехода от одной системе к другой.

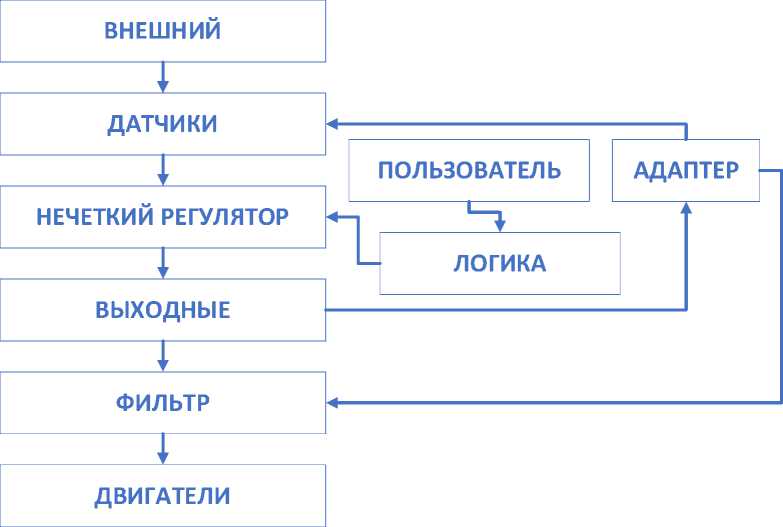
Рис. 13. Принципиальная схема робота

Как уже говорилось, сенсоры внешнего мира трактора моделируют действия лазерного дальномера лидара, который выпускает несколько лазерных лучей в разных направлениях для оценки расстояний от трактора до препятствий или виртуальных линий разметки (элементов дополненной реальности).

Задача трактора – движение по заданной траектории с обходом препятствий и движение к целевой позиции на поле цели в рамках заданных ограничений. Для простоты при создании модели можно использовать прямоугольный тип препятствия, хотя полученная система управления может работать в лабиринте с произвольным видом препятствий.

Движение трактора по полю с виртуальной разметкой осуществляется с помощью базы знаний из набора продукционных правил, которые написаны с помощью системы WARR или любой аналогичной оболочки. Можно использовать, например, Fuzzy Toolbox MATLAB .

Применение методов нечеткого интеллектуального управления позволяет создать достаточно эффективную систему управления трактором. Однако применение нейросетевого подхода при создании систем беспилотного управления, особенно с применением глубокого обучения, может быть более успешным с точки зрения точности управления трактором и распознавания нештатных ситуаций. Но система управления на основе нейронной сети не сможет объяснить механизм принятия решений, что крайне важно при построении систем, включающих средства повышенной опасности, таких как трактор или автомобиль.

Для преодоления данной проблемы предлагается использовать методы объяснимого искусственного интеллекта, например, в описываемой ситуации возможно автоматическое получение правил при помощи нейронечеткой нейросети ANFIS Fuzzy Toolbox MATLAB при наличии обучающей выборки, т.е. временного ряда параметров на входе и управляющих воздействий на выходе.

Для анализа перспективности такого подхода далее рассмотрены методы извлечения правил из искусственных нейронных сетей, основанные на нейронечетких моделях.

Обзор и анализ применения нейронечетких моделей в задачах извлечения правил из искусственных нейронных

Системы, основанные на нечетких правилах ( FRBS ), разработанные с помощью нечеткой логики, стали полем активных исследований за последние несколько лет. Эти алгоритмы доказали свои сильные стороны в таких задачах, как управление сложными системами, создание нечетких элементов управления. Исследования различных подходов к созданию объяснимого искусственного интеллекта позволяют сделать важный вывод о том, что мы можем перевести знания, встроенные в нейронную сеть, на более когнитивно-приемлемый язык - нечеткие правила. Другими словами, получаем семантическую интерпретацию нейронных сетей [1-3].

Для того, чтобы получить семантическую интерпретацию черного ящика глубокого обучения, нейронечеткие сети могут быть использованы вместо последнего полносвязного слоя. Например, ANFIS (адаптивная нейронечеткая система) является многослойной сетью прямого распространения. Эта архитектура имеет пять слоев, таких как нечеткий слой, продукционный слой, слой нормализации, слой дефаззификации и выходной слой. ANFIS сочетает преимущества нейросети и нечеткой логики. Далее приведем классификацию наиболее известных нейронечетких подходов.

Рассматривая архитектуры нейронечетких моделей, можно выделить три методики объединения искусственных нейронных сетей (ИНС) и нечетких моделей [4, 5]:

• -    neuro-FIS , в которых ИНС используется как инструмент в нечетких моделях;

• -    нечеткие ИНС, в которых классические модели ИНС фаззифицированы;

• -    нейронечеткие гибридные системы, в которых нечеткие системы и ИНС объединены в гибридные системы [6, 7].

Исходя из данных методик, нейронечеткие модели можно разделить на три класса [8-10].

Кооперативные нейронечеткие модели. В данном случае часть ИНС изначально используется для определения нечетких множеств и / или нечетких правил, где впоследствии выполняется только полученная нечеткая система. В процессе обучения определяются функции принадлежности, а также формируются нечеткие правила на основе обучающей выборки. Здесь основная задача нейронной сети заключается в подборе параметров нечеткой системы.

Параллельные нейронечеткие модели. Нейронная сеть в данном типе модели работает параллельно с нечеткой системой, предоставляя входные данные в нечеткую систему или изменяя выходные данные нечеткой системы. Нейронная сеть может являться также и пост-процессором выходных данных из нечеткой системы.

Гибридные нейронечеткие модели. Нечеткая система использует метод обучения, как это делает и ИНС, чтобы настроить свои параметры на основе обучающих данных. Среди представленных классов моделей наибольшей популярностью пользуются модели именно данного класса, доказательством тому служит их применение в широком спектре реальных задач [11-14].

Среди наиболее популярных гибридных моделей можно выделить следующие архитектуры.

Сеть управления нечетким адаптивным обучением (FALCON) [15], которая имеет пятислойную архитектуру. На одну выходную переменную приходится по два лингвистических узла. Первый узел работает с обучающей выборкой (паттерном обучения), второй является входным для всей системы. Первый скрытый слой размечает входную выборку в соответствии с функциями принадлежности. Второй слой задает правила и их параметры. Обучение происходит на основе гибридного алгоритма без учителя для определения функции принадлежности, базы правил и использует алгоритм градиентного спуска для оптимизации и подбора итоговых параметров функции принадлежности.

Адаптивная нейронечеткая система вывода ANFIS [16] - это хорошо известная нейронечеткая модель, которая применялась во многих приложениях и исследовательских областях [17]. Более того, сравнение архитектур нейронечетких сетей показало, что ANFIS показывает минимальную ошибку в задаче прогнозирования. Основным недостатком модели ANFIS является то, что она предъявляет серьезные требования к вычислительной мощности [18].

Система обобщенного приближенного интеллектуального управления на основе рассуждений ( GARIC) [19] представляет собой нейронечеткую систему, использующую два нейросетевых модуля, модуль выбора действия и модуль оценки состояния, который отвечает за оценку качества выбора действий предыдущим модулем. GARIC - пятислойная сеть прямого распространения.

Нейронный нечеткий регулятор ( NEFCON ) [20] был разработан для реализации системы нечеткого вывода типа Мамдани. Связи определяются с помощью нечетких правил. Входной слой является фаззификатором, а выходной решает задачу дефаззификации. Обучается сеть на основе гибридного алгоритма обучения с подкреплением и алгоритма обратного распространения ошибки.

Система нечеткого вывода и нейронной сети в программном обеспечении нечеткого вывода ( FINEST) [21] представляет собой систему настройки параметров. Производится настройка нечетких предикатов, функции импликации и комбинаторной функции.

Система для автоматического построения нейронной сети нечеткого вывод ( SONFIN) [22] по своей сути аналогична NEFCON контроллеру, но вместо реализации нечеткого вывода типа Мамдани реализует вывод типа Такаги-Сугено. В данной сети входная выборка обрабатывается с помощью алгоритма выровненной кластеризации. При идентификации структуры части предварительного условия входное пространство разделяется гибким образом в соответствии с алгоритмом, основанным на выровненной кластеризации. Настройка параметров системы частично реализована на базе метода наименьших квадратов, предварительные условия настраиваются с помощью метода обратного распространения ошибки.

Динамически развивающаяся нечеткая нейронная сети ( dmEfuNN) и ( EFuNN) [23]. В EFuNN все узлы создаются в процессе обучения. Первый слой передает обучающие данные на второй, который вычисляет степень соответствия с заранее определенной функцией принадлежности. Третий слой содержит в себе наборы нечетких правил, являющихся прототипами входных-выходных данных, которые можно представить в качестве гиперсфер нечеткого входного и выходного пространств. Четвертый слой рассчитывает степень, с которой выходная функция принадлежности разметила входные данные, а пятый слой производит дефаззификацию и подсчитывает числовые значения выходной переменной. DmEfuNN представляет собой модифицированную версию EFuNN . Основная идея состоит в том, что для всех входных векторов динамически подбирается набор правил, значения активации которых используются для расчета динамических параметров выходной функции. В то вре-мя как EFuNN реализует нечеткие правила типа Мамдани, dmEFuNN применяет тип Такаги-Сугено.

Заключение

В статье рассматривается алгоритм управления роботом на основе нечетких правил. Потом делается попытка обзора существующих алгоритмов извлечения нечетких правил правил из ИНС. Особое внимание уделяется извлечению правил из нейроне-четких сетей. Изучение нечеткой логики достигло кульминации в конце XX в., и с тех пор начало уменьшаться. Это снижение может быть частично связано с отсутствием результатов в машинном обучении. Извлечение правил является одним из способов помочь понять нейронные сети. Эти исследования проложат путь для исследователей нечеткой логики для разработки приложений в области ИИ и решения сложных проблем, которые также представляют интерес для сообщества машинного обучения. Опыт и знания в области нечеткой логики хорошо подходят для моделирования неоднозначностей в больших данных, модели- рования неопределенности в представлении знаний и обеспечения обучения с неиндуктивным выводом.