Нейросетевая классификация разрывов параметров космической плазмы

В межпланетном пространстве при его экспериментальном исследовании с помощью КА часто обнаруживаются разнообразные скачки параметров, или так называемые разрывы (ударные волны, тангенциальные, контактные, вращательные). Простые волны сжатия с течением времени могут увеличивать крутизну своего профиля, и в результате возникают скачки параметров плазмы, которые называются сильными разрывами или ударными волнами. Исследование этих разрывов позволяет уточнить макроструктуру солнечного ветра и связать их с процессами, происходящими на Солнце [Рязанцева, Далин, Застенкер и др., 2003]. Ударные волны образуются при явлениях солнечной активности [Rice, Zank, Li, 2003], во время эволюции волн сжатия в солнечном ветре [Lee, 2000] и при взаимодействии быстрого солнечного ветра с медленным [Бархатов, Гольберг, Зырянова, Иванов, 2003]. Разрывы образуются также при обтекании планет солнечным ветром (головная ударная волна около Земли; магнитопауза – тангенциальный разрыв, отделяющий возмущенный ударной волной солнечный ветер от магнитосферы) [Физика магнитосферы, 1972; Slinker, Fedder, Ruohoniemi, Lyons, 1996]. В связи со всем сказанным, представляет интерес установление типов разрывов, наблюдаемых в солнечном ветре, и ориентации их фронтов, исследование их устойчивости. Определение наклонов фронтов разрывов (при изучении скачков параметров межпланетной плазмы) является отдельной задачей [Haaland, Son-nerup, Dunlop, et al., 2004; Sonnerup, Hasegawa, 2005]. Для этих целей применяется метод «minimum variance», в основу которого положено изучение поведения конкретных параметров плазмы (плотности, скорости, компонент магнитного поля), полученных на одном (single-spacecraft method) или нескольких КА (multi-spacecraft method). В основе этих методов лежат модифицированный закон сохранения массы и эмпирические модели разрывов, получаемые на основе статистических данных.

Недостатком такого подхода является частая не-разделимость тангенциальных и вращательных разрывов и, соответственно, неточность в определении ориентации фронтов. Доработка подхода, заключающаяся в устранении шума в исходных данных, предлагается в [Hausman, Michel, Espley, Cloutier, 2004]. В работе указывается на то, что при использовании этого метода с разрешением больше минуты становится затруднительно выделять вращательные разрывы.

В отличие от упомянутых выше работ, в нашем исследовании разрабатывается нейросетевая методика разделения скачков в регистрируемых параметрах космической плазмы и магнитного поля на классы, отвечающие известным типам магнитогидродинамических (МГД) разрывов. Результаты выполненной классификации можно использовать для установления ориентаций фронтов разрывов. Для выполнения классификации создана искусственная нейронная сеть (ИНС) вида «слой Кохонена», позволяющая, в отличие от вышеупомянутой методики, выполнять автоматическую классификацию зарегистрированных на КА WIND скачков параметров солнечного ветра (ПСВ) среды и межпланетного магнитного поля (ММП). Результаты ИНС-классификации сопоставлены с «ручной» классификацией по алгоритмам, реализованным ИНС. В работе также предложен альтернативный отмеченному выше [Haaland, Sonnerup, Dunlop, et al., 2004; Sonnerup, Hasegawa, 2005] способ поиска ориентации фронтов. Этот способ применим после выполнения классификации скачков. В результате для разрывов установленных классов определены ориентации плоскостей их поверхностей на основе одномерных наблюдений. Дополнительно проведено исследование эволюционности найденных ударных волн.

Магнитогидродинамические основы классификации

Основы предлагаемых алгоритмов классификации заключаются в анализе соотношений параметров на МГД-разрывах (см. например, [Ландау, Лифшиц, 1986]), когда давление принимается изотропным, а подогрев разрыва за счет влияния внешней радиации несущественен. Заметим, что разрывы, перемещающиеся вместе с солнечным ветром, должны быть тангенциальными или контактными, так как только для этих двух видов выполняется условие равенства нулю скорости, перпендикулярной поверхности разрыва vn=0. Разрывы, перемещающиеся относительно солнечного ветра, должны быть вращательными разрывами, или ударными волнами. Вращательные разрывы (волны) перемещаются относительно плазмы солнечного ветра со скоростью vn, не зависящей от амплитуды волны, но определяющейся плотностью плазмы и напряженностью ММП.

Классификация, напрямую опирающаяся на условия на МГД-разрывах, не может быть применена к экспериментальным данным, полученным с одного КА, поскольку всегда остается неизвестным ориентация фронта разрыва. Векторные соотношения, входящие в условия на разрывах, оказываются бесполезными. Для решения поставленной задачи по классификации можно использовать только скалярную часть условий. Эта адаптированная часть условий следующая:

• 1)    тангенциальный разрыв, для которого характерно сохранение сумм давлений до и после скачка параметров, т. е. выполняется условие

H ²

P +--= const .

8 n

• 2)    контактный разрыв, когда скорость и магнитное поле постоянны:

V = const, H = const .

• 3)    вращательный разрыв, когда также V = const , H = const , но с дополнительным условием – концентрация плазмы до и после скачка не должна меняться ( N = const );

• 4)    ударные волны, для которых характерно увеличение концентрации плазмы, неизменное значение нормальной составляющей магнитного поля при росте магнитного поля (быстрая ударная волна) или при уменьшении поля (медленная ударная волна) за скачком.

В настоящей работе классификация разрывов проводилась согласно скалярной части условий по одному из параметров N , | B | или комбинации пара-

H ²

метров ^ P = P +-- . Классификация и ее интерпре-

8п тация потребовали разработки методики проведения численных экспериментов. Для этого было разработано два сценария (алгоритма). Согласно первому алгоритму классификация должна начинаться с раз-H2 деления скачков по сумме давлений £ P =P +—,

8п согласно второму – с разделения по магнитному полю. Схемы обоих сценариев, примененных для автоматической ИНС-классификации и «ручной» классификации, приведены ниже (см. рис. 1, 2).

Классификационная нейронная сеть «слой Ко-хонена»

Создаваемая для использования в работе искусственная нейронная сеть строится по принципу самообучения, заключающегося в подстройке весов синапсов. Очевидно, что подстройка весов может проводиться только на основании информации, доступной в нейроне, т. е. информации о его состоянии, уже имеющихся весовых коэффициентах и поданном входном векторе. Исходя из этого и, что более важно, по аналогии с известными принципами самоорганизации нервных клеток, построены алгоритмы обучения Хебба и Кохонена [Медведев, Потемкин, 2002; Круглов, Борисов, 2001]. Следует отметить, что вид откликов на каждый класс входных событий неизвестен заранее и будет представлять собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации. Общая идея данных алгоритмов заключается в том, что в процессе самообучения путем соответствующей коррекции весов усиливаются связи между возбужденными нейронами. Это означает, что происходит коррекция и закрепление образа, отвечающего конкретной части из всей группы рассматриваемых событий. Таким образом сеть способна обобщать схожие образы, относя их к одному классу.

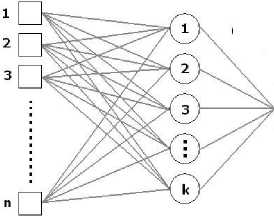
Для решения поставленной задачи по классификации была спроектирована и использована самообучающаяся ИНС. Архитектура этой сети представлена на рис. 3.

Архитектура слоя Кохонена и алгоритм его настройки предполагает, что для каждого входного вектора будет активизирован лишь один нейрон (нейрон-победитель). Для данного входного вектора только один нейрон Кохонена выдает логическую единицу, все остальные выдают ноль. Слой Кохоне-на классифицирует входные векторы в группы схожих векторов. Это достигается с помощью такой подстройки весов, что близкие входные векторы активизируют один и тот же нейрон. В результате обучения слой приобретает способность разделять несхожие входные векторы.

Подробнее рассмотрим процессы обучения и классификации по алгоритму Кохонена [Медведев, Потемкин, 2002]. В поставленной задаче каждое уединенное событие для классификации было представлено в форме вектора-столбца, сама же матрица входных данных представляет собой набор таких уединенных событий. Число нейронов в слое Кохо-нена задается при создании сети и равно числу классов, на которые предполагается разделить входные данные. Каждый нейрон описывается своим весом w_i , причем эти веса перемножаются с каждым элементом входного вектора-столбца. В результате формируется матрица весов W , в которой число строк ( k ) есть число нейронов слоя Кохонена, т. е. число предполагаемых классов, а число столбцов ( n ) равно числу элементов в каждом входном векторе-столбце. Кроме своих весов каждый нейрон описывается величиной смещения b j , которая складывается с соответствующим произведением веса и элемента входа. Таким образом, результирующий выход каждого нейрона будет определяться как

n

• s j = Y w j. ⁺ b j, i = 1

а общий ответ сети Y будет определен оператором

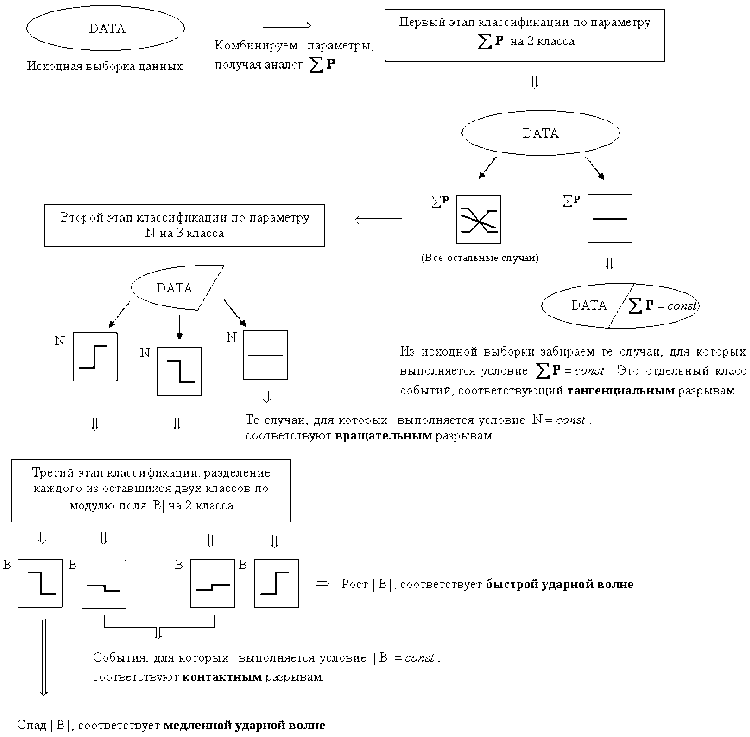
Рис . 1. Первичная классификация по сумме давлений .

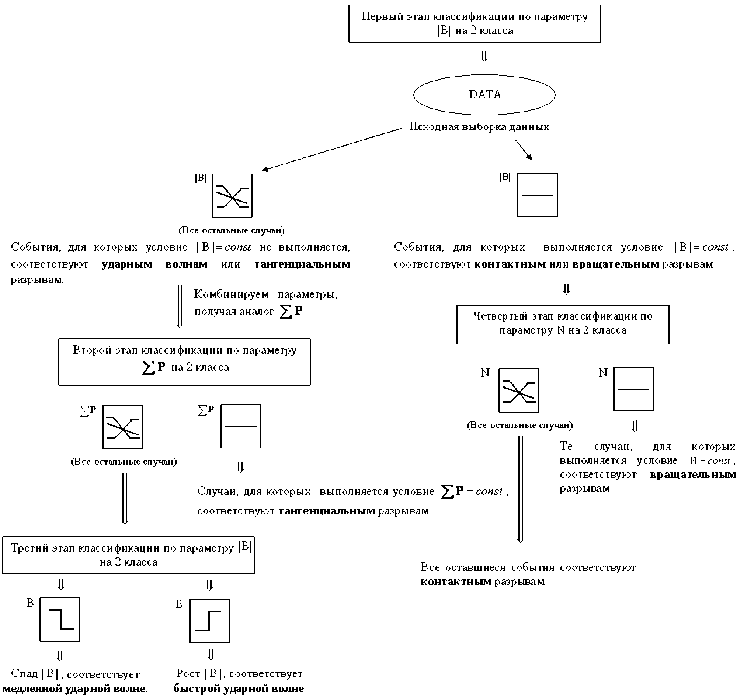
Рис . 2. Первичная классификация по магнитному полю .

Com pet

Оператор определения нейрон а -победителя

Вход

Нейроны слоя Кохонена

Рис . 3. Архитектура слоя Кохонена .

n = числу точек в классифицируемом явлении к = числу классов

k

Y = f ( Z S j ), = 1

возвращающим разреженную матрицу ответов с обозначением принадлежности каждого входного вектора-столбца к своему классу .

Для пояснения приведем пример такой матрицы, в которой представлен результат классификации 24 событий из первого пакета данных (смотреть число столбцов) на пять классов (смотреть число строк):

1	' 0 0 1
2	0 0 0
3	0 1 0
4	1 0 0
5	ч 0 0 0
	1 2 3

0  0  ...  0 ^

0   0   ...   1

0   1   ...   0 .

^{0  0}   ...   ⁰

1   0   ...   0 _?

4  5  ...  24

видно, что первый вектор-столбец (событие) отнесен к четвертому классу, второй и пятый – к третьему классу, третий – к первому, четвертый – к пятому классу, последний – ко второму классу.

Поэтапно поясним, каким образом происходят обучение и классификация:

• 1.    Первоначально матрица весов W устанавливается по правилу средней точки, т. е. берется арифметическое среднее по всем элементам входной матрицы.

• 2.    Вектор смещений первоначально так же имеет одинаковые элементы для всех нейронов, устанавливая значение всех смещений равным ek , где k – число нейронов/классов, e – основание натурального логарифма.

• 3.    Из входной матрицы случайным образом выбирается вектор-столбец и предъявляется на вход сети. Таким образом, за каждый цикл обучения все события (векторы-столбцы) из входной матрицы будут в случайном порядке обработаны сетью.

• 4.    В каждом цикле обучения для каждого нового входного вектора-столбца веса подстраиваются по правилу Кохонена:

• 5.    Смещения подстраиваются по правилу «справедливых смещений», для чего вводится дополнительный параметр каждого нейрона – активность. Параметр активности определяется как c = 1k, где в знаменателе фигурирует число нейронов Кохоне-на. Тогда приращение к параметру активности для каждого нейрона определится выражением

f l r ( d - w*), если это нейрон-победитель, Л w = <

[ 0 для остальных нейронов, где Лw - изменение веса нейрона, lr - параметр скорости настройки, d – значение текущего элемента в данном входном векторе-столбце, w* – текущее значение веса нейрона. Нейрон-победитель тот, который имеет для всего набора значений из матрицы входов максимальную величину sj=ZLwn+bi, i=1

где j равно числу нейронов/классов.

Л c = lc (a — c *), где lc – параметр справедливости, а=1 для нейрона-победителя и 0 для всех остальных, c* – текущий параметр активности данного нейрона. Изменение смещения будет определяться выражением

Лb = exp(1 — log(c * + Лc)), т. е. для неактивных нейронов смещение возрастет, чтобы сделать их конкурентоспособными при обучении, а для активных и частых нейронов-победителей смещение будет снижено, чтобы дать возможность обучаться другим нейронам. Далее шаги с 3-го по 5-й повторяются заданное число раз.

В целях оптимизации процесса обучения нейросети параметр скорости настройки и параметр справедливости в предварительных численных экспериментах подвергались постепенному увеличению (совместно и по отдельности). Выяснилось, что в условиях поставленной задачи, когда сети предлагается разделить выборку лишь по одному параметру на небольшое число классов (два или три), оптимальное состояние обучения достигается при увеличении вдвое каждого параметра настройки по отношению к стандартному значению. В этом случае при прочих равных условиях (одинаковом числе циклов настройки сети, числе запрашиваемых классов) для каждой тестовой выборки параметров сеть выдавала наиболее легко интерпретируемые результаты. Таким образом настроенная сеть была использована во всех последующих численных экспериментах.

Результаты численных экспериментов

С использованием предлагаемой методики классификации уединенных возмущений с помощью ИНС было проанализировано 82 разрыва в солнечном ветре из зарегистрированных в 1996–1999 гг. на КА WIND на предмет их разделения по типам. Предварительные численные эксперименты с нейронной сетью выявили необходимость уменьшения числа анализируемых за один раз событий, вследствие чего 82 отобранных разрыва были поделены на три части: первый пакет данных – 24 события (март 1996 – июнь 1997 гг.), второй пакет – 28 событий (июль 1997 – июль 1998 гг.), третий пакет – 30 событий (июль 1998 – сентябрь 1999 гг.).

Результаты независимой классификации по двум схемам приведены в табл. 1. Эффективность работы нейронной сети и соответствие выполненной классификации реальной ситуации проверяется сопоставлением результатов двух классификаций. В успешном

Таблица 1

Пакет данных № 1				Пакет данных № 2				Пакет данных № 3
дата	время	по схеме № 1	по схеме № 2	дата	время	по схеме № 1	по схеме № 2	дата	время	по схеме № 1	по схеме № 2
16.03.1996	15:00–15:04	конт	конт	31.07.1997	03:06–03:10	був	був	29.07.1998	06:16–06:23	був	був
04.04.1996	12:15–12:17	був	був	03.08.1997	10:04–10:07	танг	танг	29.07.1998	08:57–08:59	танг	танг
29.05.1996	12:36–12:42	мув	мув	03.08.1997	13:49–13:52	був	був	01.08.1998	12:57–13:00	танг	конт
29.05.1996	22:35–22:37	був	був	04.08.1997	02:13–02:16	мув	мув	01.08.1998	14:32–14:35	конт	конт
19.06.1996	00:25–00:27	конт	конт	07.08.1997	12:37–12:42	був	був	01.08.1998	18:05–18:07	танг	танг
01.07.1996	12:15–12:25	танг	танг	06.09.1997	14:20–14:25	був	був	10.08.1998	12:54–12:58	мув	мув
15.07.1996	17:39–17:42	танг	конт	02.03.1998	06:29–06:32	танг	танг	10.03.1999	11:46–11:51	був	був
11.02.1997	19:55–20:01	танг	танг	06.03.1998	01:43–01:45	танг	танг	10.04.1999	05:56–06:06	був	був
11.02.1997	20:54–21:02	танг	танг	25.03.1998	16:15–16:18	мув	мув	10.04.1999	06:51–06:53	конт	конт
27.02.1997	21:29–21:36	танг	танг	16.04.1998	20:15–20:19	мув	мув	17.04.1999	03:27–03:29	конт	конт
11.03.1997	00:57–01:00	мув	мув	16.04.1998	21:14–21:21	був	був	17.04.1999	10:40–10:44	танг	танг
04.04.1997	00:31–00:34	мув	мув	17.04.1998	00:52–00:57	танг	танг	17.04.1999	17:45–17:54	конт	конт
04.04.1997	01:12–01:14	був	був	26.04.1998	10:28–10:34	танг	танг	21.04.1999	07:30–07:33	танг	танг
11.04.1997	13:54–13:57	танг	конт	30.04.1998	14:48–14:53	був	був	12.05.1999	15:36–15:41	мув	мув
11.04.1997	20:52–20:56	конт	мув	02.05.1998	04:24–04:27	мув	мув	13.05.1999	06:04–06:12	був	був
21.04.1997	12:03–12:08	був	був	02.05.1998	06:03–06:12	був	конт	24.05.1999	05:11–05:15	танг	танг
21.04.1997	16:16–16:23	був	був	04.05.1998	10:13–10:16	був	був	24.05.1999	22:09–22:12	був	був
23.04.1997	10:22–10:30	мув	мув	04.05.1998	13:03–13:05	мув	мув	08.06.1999	05:34–05:43	танг	конт
23.04.1997	13:14–13:16	був	був	27.05.1998	02:02–02:12	танг	танг	08.06.1999	09:12–09:18	був	був
11.05.1997	05:45–05:55	був	був	28.05.1998	20:13–20:15	був	був	08.06.1999	15:32–15:35	танг	танг
15.05.1997	09:50–09:53	був	був	02.06.1998	10:26–10:33	був	був	28.06.1999	04:44–04:48	мув	мув
31.05.1997	01:03–01:06	був	був	24.06.1998	16:18–16:23	мув	мув	02.07.1999	11:46–11:50	був	був
06.06.1997	09:52–09:55	танг	танг	24.06.1998	22:50-23:03	був	конт	22.07.1999	05:56–06:00	був	був
25.06.1997	19:28–19:31	мув	мув	25.06.1998	03:41–03:44	танг	конт	01.08.1999	01:20–01:25	був	був
				26.06.1998	09:56–09:59	мув	мув	06.08.1999	09:35–09:36	був	був
				26.06.1998	10:21–10:25	був	конт	06.08.1999	10:02–10:06	мув	мув
				26.06.1998	15:20–15:26	був	конт	15.08.1999	19:45-19:49	мув	мув
				21.07.1998	05:18–05:22	був	був	15.08.1999	22:02–22:05	був	був
								24.08.1999	15:33–15:38	мув	мув
								12.09.1999	09:30–09:34	конт	конт

Сравнительный анализ результатов ИНС - классификации

Обозначения: конт – контактный разрыв, був – быстрая ударная волна, мув – медленная ударная волна, танг – тангенциальный разрыв.

случае результаты классификации по первой и по второй схемам должны быть близкими. Результаты работы обоих алгоритмов на трех независимых пакетах данных будут служить дополнительной проверкой.

Как видно, наиболее удачная классификация скачков проводится на материале последнего, третьего, пакета данных (93 % совпадений). На материале других пакетов данных совпадение результатов классификации по разным схемам также достаточно высоко – 87 % для первого пакета и 82 % для второго пакета. Как видно, нейросетям не удалось выделить классы, отвечающие вращательным разрывам. Такого результата следовало ожидать, так как разрывов с отсутствием скачков в концентрации в анализируемых данных, по нашему мнению, не было изначально.

Сопоставление классификации ИНС с классификацией, выполненной вручную

В данном разделе приведены результаты дополнительного исследования, необходимого для проверки достоверности выполненной нейросетевой классификации. Оно заключалось в классификации данных о скачках параметров вручную по уже разработанным и примененным выше алгоритмам. Целью проведенных экспериментов было сравнение результатов, полученных искусственной нейросетью и лаборантом

Таблица 2

Пакет данных № 1 ( ручная обработка )				Пакет данных № 2 ( ручная обработка )				Пакет данных № 3 ( ручная обработка )
дата	время	по схеме № 1	по схеме № 2	дата	время	по схеме № 1	по схеме № 2	дата	время	по схеме № 1	по схеме № 2
16.03.1996	15:00–15:04	* танг	конт	31.07.1997	03:06–03:10	був	був	29.07.1998	06:16–06:23	був	був
04.04.1996	12:15–12:17	був	був	03.08.1997	10:04–10:07	танг	танг	29.07.1998	08:57–08:59	танг	танг
29.05.1996	12:36–12:42	мув	мув	03.08.1997	13:49–13:52	був	був	01.08.1998	12:57–13:00	танг	конт
29.05.1996	22:35–22:37	* танг	* танг	04.08.1997	02:13–02:16	мув	мув	01.08.1998	14:32–14:35	* танг	конт
19.06.1996	00:25–00:27	конт	конт	07.08.1997	12:37–12:42	був	був	01.08.1998	18:05–18:07	танг	танг
01.07.1996	12:15–12:25	танг	* конт	06.09.1997	14:20–14:25	* танг	* танг	10.08.1998	12:54–12:58	мув	мув
15.07.1996	17:39–17:42	танг	конт	02.03.1998	06:29–06:32	танг	танг	10.03.1999	11:46–11:51	був	був
11.02.1997	19:55–20:01	танг	* конт	06.03.1998	01:43–01:45	танг	танг	10.04.1999	05:56–06:06	був	був
11.02.1997	20:54–21:02	танг	* конт	25.03.1998	16:15–16:18	мув	мув	10.04.1999	06:51–06:53	* танг	конт
27.02.1997	21:29–21:36	танг	* конт	16.04.1998	20:15–20:19	мув	мув	17.04.1999	03:27–03:29	* танг	конт
11.03.1997	00:57–01:00	мув	мув	16.04.1998	21:14–21:21	був	був	17.04.1999	10:40–10:44	танг	* конт
04.04.1997	00:31–00:34	мув	мув	17.04.1998	00:52–00:57	танг	* конт	17.04.1999	17:45–17:54	* танг	конт
04.04.1997	01:12–01:14	був	був	26.04.1998	10:28–10:34	танг	* конт	21.04.1999	07:30–07:33	танг	* конт
11.04.1997	13:54–13:57	танг	конт	30.04.1998	14:48–14:53	був	був	12.05.1999	15:36–15:41	мув	мув
11.04.1997	20:52–20:56	* мув	мув	02.05.1998	04:24–04:27	мув	мув	13.05.1999	06:04–06:12	був	був
21.04.1997	12:03–12:08	був	був	02.05.1998	06:03–06:12	був	* був	24.05.1999	05:11–05:15	танг	танг
21.04.1997	16:16–16:23	був	був	04.05.1998	10:13–10:16	був	був	24.05.1999	22:09–22:12	був	був
23.04.1997	10:22–10:30	мув	мув	04.05.1998	13:03–13:05	мув	мув	08.06.1999	05:34–05:43	танг	* танг
23.04.1997	13:14–13:16	був	був	27.05.1998	02:02–02:12	танг	танг	08.06.1999	09:12–09:18	був	був
11.05.1997	05:45–05:55	був	був	28.05.1998	20:13–20:15	був	був	08.06.1999	15:32–15:35	танг	танг
15.05.1997	09:50–09:53	був	був	02.06.1998	10:26–10:33	був	був	28.06.1999	04:44–04:48	мув	мув
31.05.1997	01:03–01:06	* танг	* танг	24.06.1998	16:18–16:23	* танг	* танг	02.07.1999	11:46–11:50	був	був
06.06.1997	09:52–09:55	танг	* конт	24.06.1998	22:50–23:03	був	* був	22.07.1999	05:56–06:00	був	був
25.06.1997	19:28–19:31	мув	мув	25.06.1998	03:41–03:44	танг	конт	01.08.1999	01:20–01:25	* танг	* танг
				26.06.1998	09:56–09:59	мув	мув	06.08.1999	09:35–09:36	був	був
				26.06.1998	10:21–10:25	був	* був	06.08.1999	10:02–10:06	мув	мув
				26.06.1998	15:20–15:26	* танг	конт	15.08.1999	19:45–19:49	мув	мув
				21.07.1998	05:18–05:22	був	був	15.08.1999	22:02–22:05	був	був
								24.08.1999	15:33–15:38	мув	мув
								12.09.1999	09:30–09:34	* мув	* мув

Сравнительный анализ результатов классификации при ручной обработке

Обозначения: конт – контактный разрыв, був – быстрая ударная волна, мув – медленная ударная волна, танг – тангенциальный разрыв. Несовпадение результатов классификации с ответами нейросети отмечены звездочкой.

(естественной нейросетью). Особенность ручной классификации заключается в более строгом разделении параметров для конкретных классов. В отличие от нейронной сети, которая единовременно работает с одним конкретным событием (все остальные события в это время условно присутствуют в виде коэффициентов настройки ИНС, а их «четкость» зависит от качества обучения сети), у лаборанта есть возможность работать сразу со всеми случаями. Такое преимущество позволяет естественной нейросети оперировать полным набором событий одновременно. Для достижения более полной объективности в оценках поведения параметров определены условия отбора. Так, скачком параметра считается изменение его зна- чения в момент разрыва не менее чем в 1.5–2 раза, а незначительные отклонения значений в момент скачка в большую или меньшую сторону на 10–15 % приравниваются к постоянству данного параметра. Так как обе нейронные сети классифицировали данные по одним и тем же алгоритмам, то следовало ожидать схожих результатов для схем классификации № 1 и № 2. Ниже приведена итоговая таблица классификации данных вручную (табл. 2).

Сопоставление результатов, полученных разными методами (ИНС, ручная обработка), позволило вычислить долю несовпадений для разных вариантов классификации (см. табл. 3). Для первого пакета данных несовпадение результатов при ручной клас-

Таблица 3

Общая доля несовпадений для разных вариантов классификации

Классификация вручную по схеме 1 Классификация вручную по схеме 2 Классификация нейросетью по схеме 1 Классификация нейросетью по схеме 2 Классификация вручную по схеме 1 23.18 % 17.08 % 25.62 % Классификация вручную по схеме 2 23.18 % 25.62 % 21.96 % Классификация нейросетью по схеме 1 17.08 % 25.62 % 12.20 % Классификация нейросетью по схеме 2 25.62 % 21.96 % 12.20 % классификации по разным схемам наблюдается для восьми событий из 24. У всех этих событий P=const и B =const, причем по первой схеме они определяются как тангенциальные, а по второй как контактные, поэтому были отнесены лаборантом в разные классы. По сравнению с результатами классификации, произведенной ИНС, для схемы № 1 наблюдается пять несовпадений, а для схемы № 2 – шесть несовпадений.

Несовпадение результатов при классификации второго пакета данных по разным схемам наблюдается для четырех событий из 28. У всех этих событий также присутствует условие P = const и B = const . По той же причине, что и в первом случае, по первой схеме они определяются как тангенциальные, а по второй как контактные. Результаты классификации вручную и произведенной ИНС для схемы № 1 не совпадают в три случаях, а для схемы № 2 – в семи случаях.

При ручной классификации данных из пакета № 3 несовпадение итогов по разным схемам наблюдается для семи событий из 30. У всех этих событий P = const и B = const . По первому алгоритму они определяются как тангенциальные, а по второму как контактные. С ответами ИНС для этого пакета данных для схемы № 1 наблюдается шесть несовпадений, а для схемы № 2–пять несовпадений.

Перепутывание тангенциальных и контактных разрывов является следствием слабой разветвленности предложенных алгоритмов классификации. Необходимо еще хотя бы одно дополнительное условие разделения данных. Но такое условие может появиться только при выходе за рамки одножидкостной модели плазмы, которая принята в данном исследовании. В планируемом исследовании предполагается повышение достоверности классификации разрывов межпланетной плазмы введением дополнительных параметров, согласующихся с двухжидкостной моделью исследуемой среды и протекающих в ней процессов.

Установление ориентации плоскостей фронтов рассматриваемых разрывов

Данный раздел посвящен установлению ориентации плоскостей поверхностей разрывов в пространстве солнечно-эклиптической (SE) системы координат. Основным источником информации при определении ориентации плоскостей конкретных разрывов, помимо сведений о поведении компонент векторов ММП и скорости потока, является установленный нами в результате классификации тип разрыва.

Известно, что одним из условий существования вращательного разрыва и ударной волны является неизменность величины и направления нормали магнитного поля к поверхности этих типов разрывов во время скачка ([ H n ]=0). Таким образом, если построить в трехмерном пространстве компонент магнитного поля радиус-вектор и определить положение скачка, то поверхность разрыва будет перпендикулярна прямой, соединяющей две точки – до и после разрыва. На рис. 4 схематично, для простоты представления на плоскости, продемонстрирована методика определения положения таких скачков.

На плоскости B x B y векторами r 1 , r 2 , r 3 и r 4 указаны положения радиус-вектора в пространстве значений компонент магнитного поля. Скачок величины ММП

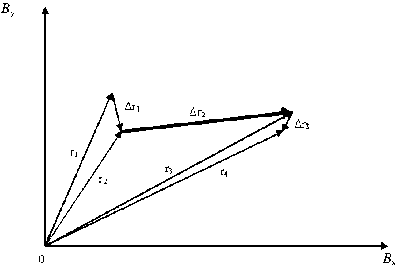
Рис . 4. Методика определения положения разрыва в пространстве компонент магнитного поля ( аналогично для компонент скорости ).

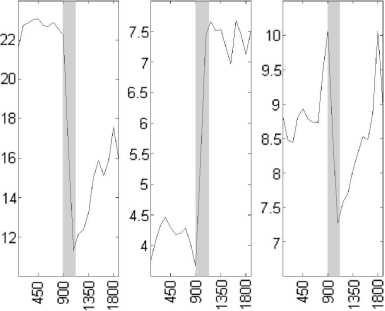
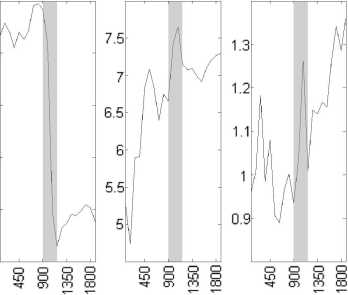
наблюдается при самом большом по модулю векторе Δr 2 . Он обозначен жирной стрелкой. Построив перпендикулярную к нему плоскость, мы определим тем самым ориентацию плоскости скачка. Так как данные по ММП и ПСВ представлены в системе координат SE, то, выбрав безразмерные оси координат, можно показывать ориентацию плоскости скачка, не привязывая плоскость к пространству значений магнитного поля . На рис. 5 для примера показаны временные зависимости измеренных параметров на КА для события 4 апреля 1996 г. типа ударная волна ( а ) и найденная плоскость поверхности разрыва ( б ) для этого скачка. По осям отложены условные единицы. Маркером на рис. 5, а отмечен момент скачка параметров.

Для определения ориентации плоскостей тангенциальных и контактных разрывов следует пользоваться условиями H _n = V _n =0 (для тангенциального разрыва) и V n =0 (для контактного разрыва). Другими словами, у тангенциальных и контактных разрывов должны вообще отсутствовать нормали магнитного поля и скорости. Это означает, что плоскость такого разрыва должна быть всегда параллельна вектору Δr 2 (см. рис. 4) в пространстве компонент магнитного поля или скорости. Однако в трехмерном пространстве для данной прямой можно изобразить бесконечно много параллельных прямых. Поэтому для получения однозначного решения следует искать уравнение такой плоскости, которой принадлежали бы две прямые – одна из пространства компонент

N (c м ³) | В | ( нТл ) ∑Р ( Па )×10^–18

N (c м ³)         | В | ( нТл )        ∑Р ( Па )×10^–17

б

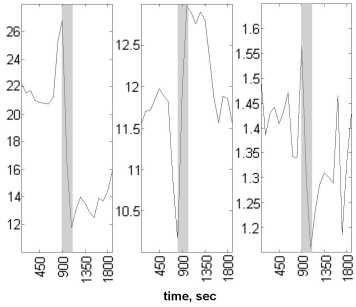
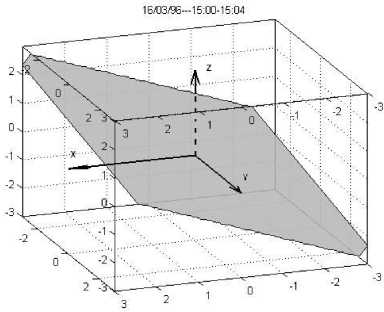
Рис . 6. Параметры события 16 марта 1996 г . типа кон тактный разрыв , полученные на основе измерений на КА ( а ); расчетная плоскость разрыва в координат SE в услов ных единицах ( б ).

time, sec

N (c м ³)          | В | ( нТл )         ∑Р ( Па )×10^–17

time, sec

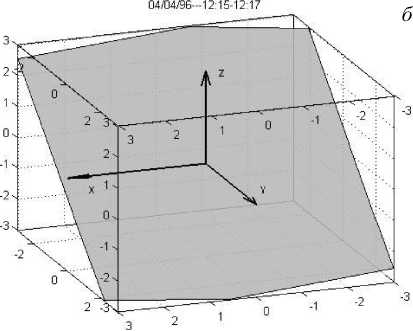
Рис . 5. Параметры события 4 апреля 1996 г . типа удар ная волна , полученные на основе измерений на КА ( а ); расчетная плоскость разрыва в системе координат SE в условных единицах ( б ).

б

06/06/97—09 52-09 55

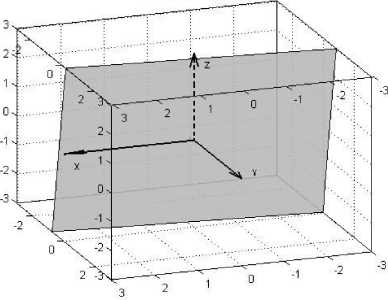
Рис . 7. Параметры события 6 июня 1997 г . типа тан генциальный разрыв , полученные на основе измерений на КА ( а ); расчетная плоскость разрыва в координат SE в условных единицах ( б ).

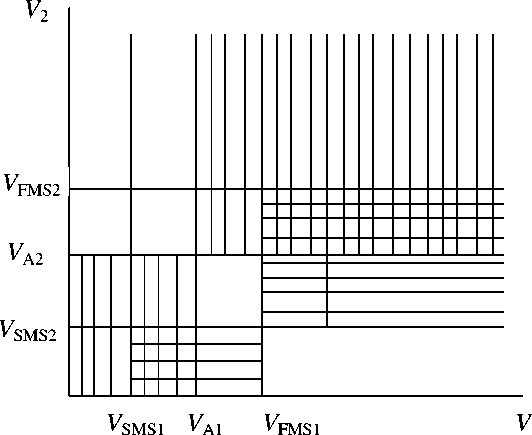
Рис . 8. Области определения эволюционности удар ных волн .

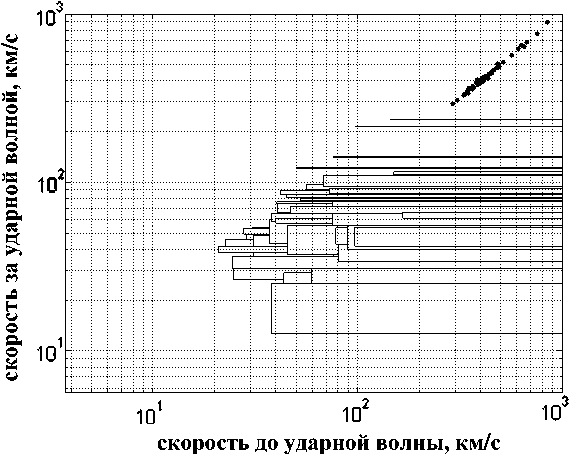
Рис . 9. Области эволюционности и значения скачков скоростей среды для изучаемых ударных волн .

магнитного поля, другая из пространства компонент скорости. Картина, построенная в безразмерных координатах, даст картину в системе SE. На рис. 6 для примера показаны временные зависимости измеренных на КА параметров для события 16 марта 1996 г. типа контактный разрыв ( а ) и найденная плоскость поверхности разрыва ( б ) для этого скачка. Маркером на рис. 6, а отмечен момент скачка параметров. На рис. 7 то же приведено для события 6 июня 1997 г., представляющего собой тангенциальный разрыв.

Таким образом, по одномерным измерениям удается получать трехмерные картины, описывающие положения разрывов параметров в солнечном ветре.