Нейросетевой анализ раскрашенных графов

DOI:

Современные методы дискретной математики, в частности теория графов, находят широкое применение при исследованиях в самых разных областях науки и техники. Так, например, в области химии, применительно к тематике наших интересов [3; 5], структуры химических соединений моделируют с помощью графов, что позволяет применять указанные математические методы для анализа и синтеза виртуальных химических структур [1; 10], имеющих не только академическое, но и практическое значение, например, при выборе перспективных веществ для продвижения на технологический рынок. При этом решение ряда важных прикладных задач в данной области часто сводится к статистическому анализу различных дескрипторов химических структур. Учитывая это, математическое решение такого рода задач состоит из четырех этапов: формального представления исходных данных (в нашем случае химических структур), построения математической модели, анализа формализованной модели и синтеза решающих правил.

Формально описанную выше задачу можно представить следующим образом.

Пусть задан универсум G графов. Выделим в нем подмножество G ⁺ ⊂ G графов, обладающих интересующим нас свойством. Соответственно множество G \ G ⁺ обозначим через G ^–. Будем считать, что, вообще говоря, элементы множества G ⁺ не известны, но некоторые из них все же установлены и составляют множество G⁺ ⊂ G ⁺. Аналогично G^– ⊂ G ^–. Таким образом, множество G = G⁺ ⊂ G^– составляет обучающую выборку.

Пусть задан граф G ⁰ ⊂ G \G. Требуется определить, какому из двух множеств ( G ⁺ или G ^–) он принадлежит. Иными словами, обладает ли граф G ⁰ заданным свойством или нет.

Таким образом, основной задачей данной работы является создание теоретических предпосылок для получения статистик графов и формирования правил идентификации свойств графов согласно обучающей выборке. Для иллюстрации и интерпретации формальных выкладок будем использовать химические структуры.

Для решения поставленной задачи будем использовать основные положения теории графов [7].

В настоящей работе для анализа графа будем использовать статистику простых цепей и при моделировании химической структуры примем следующие положения:

• –    каждый атом (или группу атомов) будем представлять вершиной, окрашенной в цвет, соответствующий химическому элементу (или функциональной группе);

• –    количество цветов вершин обозначим через k_v ( k_v может достигать нескольких тысяч: химические элементы плюс группы элементов);

• –    для идентификации атомов в молекуле пометим все вершины в графе: v ₁, ..., v_n , где n – количество вершин в графе;

• –    цвет вершины v_i обозначим через c_i , i = 1, ..., n ;

• –    химические связи между атомами в молекуле будем представлять ребрами, причем ребра будут раскрашены в цвета, соответствующие различным типам химических связей. Количество цветов ребер обозначим через k_e ( k_e может достигать нескольких единиц, в зависимости от учитываемых типов химической связи). Цвет ребра инцидентного вершинам v_i и v_j обозначим c_ij (цвет 0 обозначает отсутствие ребра).

В результате получим простой (без петель и кратных ребер) помеченный граф G как с вершинной, так и с реберной раскраской. Причем, степень любой вершины не превышает максимальной валентности химического элемента – 8, то есть

∆ ( G ) ≤ 8,                                            (1)

где ∆ ( G ) – максимальная степень вершины графа G [7].

Возможны и другие ограничения, определяемые исходя из задач анализа рассматриваемого конкретного класса химических соединений. Например, если в этом же контексте рассматривать предпочтения авторов – мономеры, предназначенные для синтеза или модификации высокомолекулярных соединений [2; 4; 9; 10], то количество вершин в графе можно ограничить несколькими десятками.

Следующая задача – это определение всех возможных простых цепей в графе G (далее, поскольку речь будет идти только о простых цепях, для краткости говорится «цепь» вместо «простая цепь»).

Для решения этой задачи воспользуемся поиском в ширину [7].

• 1.    Определим множество H = ∅ цепей, множество V ₀ = ∅ рассмотренных начальных вершин цепей и V _n = VG еще не рассмотренных начальных вершин.

• 2.    Зафиксируем начальную вершину v_{i 0} ∈ VG \ V ₀ цепи, положим V ₀ = V ₀ ∪ { v_{i 0}}, V_n = V_n \{ v_{i 0}}, множества H_k = ∅ цепей длины k = 0, …, n с начальной вершиной v_{i 0}.

• 3.    Положим рассматриваемые цепь h_c = v_{i 0} и вершину v_c = v_{i 0}, множество V_h = { v_{i 0}} вершин цепи h_c , k = 1.

• 4.    Определим множество V_c ⊂ VG \ V_h вершин, смежных вершине v_c . Если V_c = ∅ , то перейдем на шаг 6.

• 5.    Положим H_k = H_k ∪ { h_c.v | v ∈ V_c } и H = H ∪ { h_c . v | v ∈ V_c }, где «.» – операция конкатенации.

• 6.    Если H_{k -1} = ∅ , то перейдем на шаг 7, иначе возьмем h_c ∈ H_{k -1}, в качестве v_c последнюю вершину из цепи h_c , а множества V_h все вершины цепи h_c , положим H_{k -1} = H_{k -1}\{ h_c } и перейдем на шаг 4.

• 7.    Положим k = k + 1. Если k <  n + 1, то переходим на шаг 6.

• 8.    Если V_n = ∅ , то завершим алгоритм, иначе перейдем на шаг 2.

После завершения алгоритма множество H будет содержать все цепи. Заметим также, что множество H ₀ цепей нулевой длины всегда пусто, поскольку такие цепи нас не интересуют.

Как видно, раскраска никак не учитывалась в алгоритме. Поэтому алгоритм применим к более широкому классу графов (и к несвязным тоже). Раскраска же нам понадобится дальше, при статистическом анализе цепей.

Покажем теперь, что приведенный алгоритм действительно находит все цепи в графе.

Рассмотрим в графе G некоторую цепь v_i v_i ...v_i , где 2 ≤ m ≤ n . Согласно шагам 2 и 8 вершина v_i обязательно станет начальной в цепи, а по шагу 3 вершина v_i станет рассматриваемой. Далее, поскольку v_i смежна v_i , то v_i на шаге 4 будет помещено в множество V_c и затем на шаге 5 цепь v_i v_i будет помещена в множества H ₁ и H . Затем по шагу 6 цепь v_i v_i и вершина v_i станут рассматриваемыми. Далее повторяем приведенные выше рассуждения для связки вершин v_i – v_i и цепь v_i v_i v_i будет помещена во множество H .

Поскольку данный алгоритм решает поставленную задачу, рассмотрим теперь, насколько эффективно это решение.

Оценим сложность L алгоритма.

Шаг 1 выполняется всего один раз и его составляют инициализация пустых множеств H, V0 (сложность константа c0), а также множества Vn (сложность c1n). Шаги со 2-го по 8-й выполня- ются, пока в качестве начальной вершины цепи не поучаствует каждая из вершин графа G, то есть n раз:

L = c₀ + c₁ n + nL ₁,

где L ₁ – сложность шагов 2–8.

В свою очередь L ₁ составляют шаг 8 (сложность c₂) и шаги со 2-го по 7-й (сложность L ₂). Шаги со 2-го по 7-й повторяются, пока не рассмотрим все длины цепей k , то есть n раз. Получили, что L ₁ = c₂ + nL ₂. Подставляя полученное равенство в (2), получим

L = c₀ + (c₁ + c₂) n + n ² L ₂.

Далее L ₂ составляют шаг 7 (сложность c₃), шаг 2, на котором инициализируются H ₀,

..., H_n ,

и проводятся несколько операций (сложность c₄ + c₅ n ), шаг 3, на котором строим множество V_h из k вершин, учитывая, что k ≤ n , плюс еще несколько операций, получим сложность шага 3 не больше c₆ + c₇ n , и шаги с 4-го по 6-й (сложность L ₃). Шаги с 4-го по 6-й повторяются, пока не рассмотрим все цепи из множества H_k (число таких цепей обозначим N_k ). Получили, что L ₂ ≤ c₃ + + c₄ + c₆ + (c₅ + c₇) n + NL ₃, где N = max N_k . Подставляя полученное неравенство в (3), получим k = 1,..., n

L ≤ c₀ + (c₁ + c₂) n + (c₃ + c₄ + c₆) n ² + (c₅ + c₇) n ³ + n ² NL ₃.

На шаге 4 реализуется несколько операций и поиск смежных вершин. Все смежные вершины можно найти не более, чем за n операций. Поэтому сложность этого шага можно оценить, как не превосходящую величину c₈ + c₉ n .

На шаге 5 добавляем в множества H_k и H новые цепи. Число этих цепей равно числу смежных вершин, а число смежных вершин не может быть больше 8 для рассматриваемого класса графов G , то есть сложность этого шага составляет константу c₁₀.

На шаге 6 реализуется несколько операций и формирование множества V_h , на что может понадобиться до n операций. Следовательно, сложность этого шага можно оценить величиной c₁₁ + c₁₂ n .

Суммируя вышесказанное, получаем L ₃ ≤ c₈ + c₁₀ + c₁₁ + (c₉ + c₁₂) n и подставляем это неравенство в (4):

L ≤ c₀ + (c₁ + c₂) n + (c₃ + c₄ + c₆) n ² + (c₅ + c₇) n ³ + (c₈ + c₁₀ + c₁₁) n ² N +

+ (c₉ + c₁₂) n ³ N ≤ c₁₃ n ³ N .

Из этой оценки уже видно, что сложность алгоритма полиномиальна относительно числа вершин и числа цепей, что позволяет сделать заключение о достаточной эффективности алгоритма.

Теперь осталось оценить величину N .

Очевидно, что N ₁ ≤ ∆ ( G ). Далее, так как одна смежная вершина – это та, из которой мы попали в следующую, то смежных вершин, отсутствующих в цепи, будет не более Δ( G ) – 1, и получаем N_k ≤ ∆ ( G )( ∆ ( G ) – 1) ^{k –1} . Откуда, учитывая (1),

N = m ax N k ≤∆ ( G )( ∆ ( G ) - 1) ^{n - 1} = ^{∆ ( G )} ( ∆ ( G ) - 1) ⁿ ≤ c 14 7 ⁿ.

k = 0 ,n                                ∆ ( G ) - 1

Подставляя эту оценку в (5), получим

L ≤ c n ³7 ⁿ .

Очевидно, что общее количество цепей в графе не превышает величину n ( А ( G )) n . Убедимся, что среди рассматриваемых графов действительно есть такие, у которых имеется экспоненциальное число цепей. Таким примером может служить, например, следующий граф порядка n на рисунке 1.

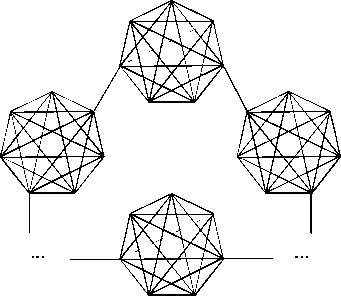
Рис. 1. Пример графа с экспоненциальным числом цепей

Пусть n будет кратно 7. Тогда возьмем ряд 7-клик (всего их будет n /7), последовательно соединим их ребрами (мостами) так, чтобы эти ребра не были смежными, и крайние клики со- 5

единим ребром аналогично. В каждой 7-й клике можно выделить S A k цепей длины от 1 до 6, k =0

начинающихся с вершины, инцидентной одному мосту, и заканчивающихся вершиной, инцидент- n

I k ^

ной другому мосту. Соединяя цепи из соседних клик, можно составить всего I S A ₅ ^k I , причем мы

• ⁷ к =0 ^V

учли не все цепи, поэтому это нижняя оценка числа цепей графа. Учитываем также, что

S A k - S C^k (в этом можно убедиться путем непосредственного вычисления). Следовательно, k =0        k =0

общее число цепей будет превосходить следующую величину nn

⁵7⁷7            ⁿ

^[ S A 5 k I -^[ S C 7 k I = ( 2 ⁷ ) ⁷ = 2 n .

⁷ к = o    ^{V 7} к = 0 V

То есть в общем случае построить полиномиальный алгоритм для решения данной задачи, в принципе, невозможно, и предлагаемое решение является эффективным.

Таким образом, мы рассмотрели алгоритм поиска всех цепей в графе и теперь можно перейти собственно к решению задачи идентификации графа.

Пусть имеется два класса раскрашенных графов G⁺ и G^–. Предъявлен некоторый граф G ⁰ £ G + u G^-. Требуется определить, к какому из двух классов следует отнести граф G ⁰.

Собственно, решающее правило будем формировать на основе полученных цепей. Для анализа статистики цепей предлагаем воспользоваться ИНС. Основные идеи ИНС для анализа химических систем в литературе представлены для различных вариантов [6; 8]. Предлагаемый подход позволяет не просто учитывать появление тех или иных цепей, но и то, какие фрагменты включают эти цепи и в каком порядке расположены фрагменты. Остановимся на формальной стороне вопроса.

Пусть G+ = {GJ,..., G^}, G- = {Gj-,..., Gs- } и пусть для каждого графа Gl+, l = 1, .„, s+, Gl, s+ l = 1,..., s- и G0, получено соответственно множество H/, Hl и H0 всех его цепей и H+ = UH+, s -                                                                                                                                                                                       l=j

H^- = U/ и H = H⁺ u H^-.

l = j

Будем строить ИНС из m слоев, где m – максимальная длина из всех полученных цепей. Принцип работы ИНС следующий. На входные синапсы будем подавать цепи графа G ⁰, а на выходе будем считывать сигналы. Если сумма этих сигналов положительна, то будем полагать, что G 0 е G + , если же отрицательная, то G 0 е G^-.

Поскольку на входы ИНС будем подавать цепи, то примем, что нейрон соответствует вершине, а синапс – ребру. При этом число нейронов в каждом слое будет одинаковым и равно числу всех цветов вершин (плюс один для цвета ноль), встречающихся среди графов из G = G⁺ u G^-. Все нейроны в одном слое окрашены в различные цвета (в том числе и в цвет ноль).

Пусть каждый из m слоев ИНС состоит из k _v + 1 нейронов u_p^j , где p = 0, ..., k _v (нейрон с номером p = 0 является фиктивным и служит для решения некоторых проблем при прохождении сигнала через ИНС) – цвет нейрона, j = 1, ..., m . Условимся также считать, что любая пара нейронов, расположенная в двух соседних слоях, соединена k _e синапсами (каждый синапс соответствует ребру определенного цвета) с весом го ^s_qr_T - вес синапса (для ребра цвета r ) между нейронами u^j_q и u^j_q^x (рис. 2).

Вес го qqr формируется при обучении ИНС следующим образом. В начале обучения го qqr = 0 для всех q , q , r и j . Рассмотрим некоторую цепь h + = ( и .„ ...u. _lt ) е Ы^, где a - длина цепи; t - номер цепи. Сигнал для h + подается на вход нейрона и^х_С8 (имеющего тот же цвет, что и первая вершина ⁱ 1 ^t                                      2

в цепи h + ). Далее сигнал идет в следующий слой на нейрон ^ис„ по синапсу цвета с» ! и так далее lt                                                                                                                                                     i ₂                                                        1 2

от слоя к слою, пока не закончатся вершины в цепи h l + . При прохождении сигнала от нейрона u^J_q к нейрону u j^+x по синапсу цвета r будем увеличивать его вес го qqr на 1.

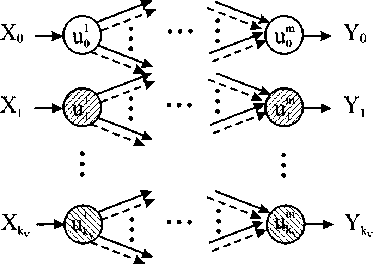
Рис. 2. Принципиальная схема ИНС:

X – входной сигнал; Y – выходной сигнал; u – нейрон; m – количество слоев ИНС; k – количество цветов вершины исходного графа

Так мы поступаем для каждой цепи из Ы ^ . Далее повторим эту процедуру для каждого l = 1, ..., s ⁺.

Аналогично поступим и с цепями из множеств H l , l = 1, . „, s ^-, только с тем отличием, что при прохождении сигнала будем вес го ^j _qqr синапса не увеличивать, а уменьшать на 1.

В результате получили решающее правило в виде нейронной сети, которое идентифицирует предъявляемый граф G ⁰ следующим образом.

Подаем на входы ИНС все цепи из H ⁰. На входе каждый сигнал имеет величину 0. Сигнал для каждой цепи проходит через ИНС так, как это было описано выше при обучении сети, но теперь при прохождении сигнала по синапсу происходит не модификация его веса го qqr , а считывание. Считанное значение добавляется к величине сигнала.

Если длина a _{0 t} цепи оказывается меньше m , то вслед за последней вершиной этой цепи сигнал идет на фиктивный нейрон и 0 ⁰ t ^{+ 1} и далее сигнал идет через фиктивные нейроны вплоть до u ₀ ^m . А поскольку веса синапсов между фиктивными нейронами нулевые, то сигнал до самого выхода не изменяется.

Обозначим через y_t получившуюся величину сигнала на выходе из сигнала X_c на входе ИНС для цепи h ⁺= ( и,...и, ) е Ы ⁰. Тогда                                                   1

t                i1t iatt at —1

y =V to j t                 ctct ctt .

j = 1 ij ij + 1 ijij + 1

Суммарный же сигнал Y на выходе ИНС будет следующим:

k v            H 01          H 0 1 a t — ¹

Y=ZYp =Zyt !!■, p=0           t=1           t=1 j=1      j j+1 jj+1

где Y_p – величина выходного сигнала.

В результате, если Y > 0, то идентифицируем граф G ⁰, как G⁺. Если же Y < 0, то идентифицируем граф G ⁰, как G^–.

Предложенная здесь теория может быть реализована в нейрокомпьютерной технологии для решения задач проектирования путем проведения статистического анализа простых раскрашенных графов. Естественно, приведенные выше выкладки требуют определенной адаптации для решения конкретных задач. Сказанное выше следует рассматривать, как математическое обеспечение, на основе которого можно обоснованно синтезировать конкретные решающие правила, в том числе путем введения в ИНС активационных функций, персептронов или, быть может, других компонентов, которые позволят эффективно обучать ИНС для решения конкретных задач анализа и синтеза графовых структур.