Нейросетевой эмулятор отклика спинового ансамбля на последовательность радиоимпульсов

DOI:

Предсказание отклика физической системы на некоторое заданное воздействие необходимо во многих приложениях, включая радиолокацию [6], связь [10], дистанционное зондирование [12] и спектроскопию [5; 13]. Имея репрезентативную модель среды, возможно скорректировать искажения информационного сообщения или подобрать воздействие для получения требуемого отклика системы. Построение модели линейной системы, как правило, не вызывает затруднений – для этого достаточно вычислить или измерить импульсную, переходную или частотную характеристику системы. Однако для нелинейных систем из стандартных подходов можно отметить разве что использование рядов Вольтерра, которые не приводят к ортогональному разложению, и разделение функций отклика различного порядка является далеко не тривиальной задачей [4].

В магнитно-резонансной спектроскопии для управления динамикой спиновых моментов электронов или ядер используют радиочастотные импульсы. Параметры воздействия, то есть количество импульсов, их амплитуда и форма огибающей, а также длительность интервала между импульсами, выбираются в предположении, что магнитное поле в системе является однородным или имеет заданный градиент. Однако создать однородное магнитное поле по всему объему образца достаточно трудно. К тому же РЧ-импульс так или иначе претерпевает искажения при цифро-аналоговом преобразовании и вследствие конечной ширины полосы РЧ-тракта. Компенсация неоднородности поля и несовершенства формы импульса позволит увеличить чувствительность спектрометров и повысить их спектральное разрешение.

Для многих задач, и магнитно-резонансной спектроскопии в том числе, кроме нелинейной связи отклика и воздействия, характерно то, что наблюдение за реакцией системы возможно только после окончания воздействия, поскольку, во-первых, используется одна катушка, а во-вторых, выделить слабый отклик на фоне мощного импульса очень трудно. Еще одной особенностью магнитно-резонансной спектроскопии является разный временной масштаб динамики системы во время и после воздействия. Так, длительность управляющих РЧ-импульсов в современных спектрометрах составляет несколько микросекунд, а особенности исследуемого вещества извлекаются из сигналов спада свободной индукции, длительность которых может достигать нескольких секунд.

Для моделирования и анализа динамики физических систем исследователи все чаще используют методы машинного обучения [8] и искусственные нейронные сети [11] в частности. При таком подходе построение модели системы или среды возможно на основании массива данных, полученного в результате экспериментов. Задача нейронной сети или алгоритма заключается в выявлении закономерностей в этом наборе данных с тем, чтобы предсказать отклик на произвольное воздействие. Эта задача обычно усложняется тем, что зачастую не удается сформировать большой набор обучающих данных. Так, в работе [3] исследовалась обобщающая способность нейросетевого классификатора, а в работе [2] проводилось обучение наивного байевского классификатора. Исследователи отмечают, что при использовании малого набора данных выбраная архитектура переобучается, то есть генерирует верный отклик на воздействие, которое использовалось

d)

e)

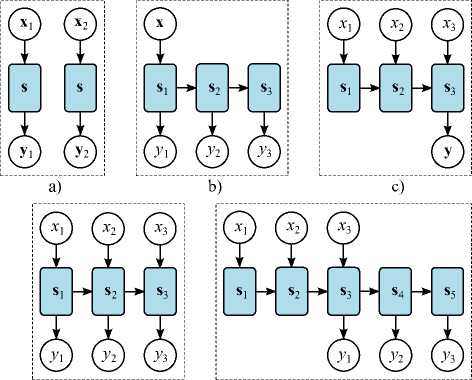
Рис. 1. Основные архитектуры нейронных сетей для обработки последовательностей данных: а) один вход, один выход (one-to-one); b) один вход, много выходов (one-to-many); с) много входов, один выход (many-to-one); d) много входов, много синхронных выходов (synchronized many-to-many); e) много входов, много асинхронных выходов (asynchronized many-to-many) при обучении, и ошибается при прогнозировании отклика на воздействие, не представленное при обучении. В таких случаях обычно требуется дополнительная обработка обучающего набора данных и регуляризация.

В зависимости от входных и выходных данных можно выделить пять основных архитектур нейронных сетей, используемых для обработки временных последовательностей [9]. В первой архитектуре, представленной на рисунке 1a), элементы последовательности данных не связаны между собой. То есть, если откликом системы на набор дискретных отсчетов входного воздействия x ₁ является набор y ₁ , то отклик y ₂ на воздействие x ₂ не зависит от предыстории, то есть значений x ₁ и y ₁ . Следовательно, состояние системы s не зависит ни от входных, ни от выходных данных. Такая архитектура может быть использована для вычисления отклика y стационарной системы на входную последовательность x с помощью полносвязной или сверточной сети [1].

В архитектуре, представленной на рисунке 1b), нейронная сеть используется для последовательного вычисления отсчетов выходного сигнала у _п на входной набор подаваемых единовременно отсчетов x , причем размерность входных и выходных последовательностей может не совпадать. Как видно из рисунка, внутреннее состояние сети при этом изменяется и его можно представить на каждом временно´ м шаге некоторым набором чисел s _n . Такая архитектура может быть использована, например, для вычисления значений сигнала у _п по набору отсчетов его спектра х . Так как динамика системы в этом случае полностью описывается ее состоянием s _n , с помощью указанной архитектуры можно реализовать также выделение или подавление некоторых спектральных составляющих.

Архитектура, приведенная на рисунке 1c), последовательности входных данных х _п ставит в соответствие набор отсчетов y . Такая архитектура может быть использована для решения широкого круга задач: для вычисления спектра сигнала по его отсчетам х _п ; для оценивания одного или сразу нескольких параметров сигнала; для классификации сигналов.

В архитектуре, представленной на рисунке 1d), каждому входному отсчету хп соответствует отсчет отклика уп. Эта архитектура может применяться в любых приложениях обработки сигналов, когда осуществляется преобразование сигналов «из точки в точку»: цифровые фильтры, нелинейные динамические системы, вычисление отклика нестационарных систем.

Наконец, в архитектуре, представленной на рисунке 1e), внутреннее состояние в последующий момент времени s _n +1 зависит как от входного воздействия х _п , так и от текущего состояния s _n . Эта архитектура может быть применена в задачах, когда отклик и воздействие не могут быть заданы для одного момента времени, например, в задачах зондирования и спектроскопии. Также архитектура может быть полезной, если отклик и воздействие задаются на одном временном интервале, но с разными частотами дискретизации.

В этой работе для построения эмулятора отклика спиновой системы используется архитектура для синхронного преобразования отсчетов РЧ-импульсов в дискретную последовательность отсчетов отклика системы. Такой подход позволил корректно предсказывать динамику спинового ансамбля на длительную импульсную последовательность.

1.    Архитектура эмулятора и метод его обучения

Эмулятор отклика построен с использованием архитектуры, предназначенной для синхронного преобразования сигналов, структура которой приведена на рисунке 2. Отсчеты входного сигнала х _п , где п - номер отсчета, подаются на сигнальные входы ячейки первого слоя 1 1 , которая содержит С рекуррентных нейронов. Рекуррентная ячейка первого слоя на основании входных данных и предыдущего состояния h ^ - 1 вычисляет новое состояние h ^ , которое представляет собой массив с размерностью 1 х С . Этот набор чисел подается на вход следующего рекуррентного слоя - / 2 и т. д. При использовании L рекуррентных слоев состояния ячеек слоя объединяются в массив H _n с размерностью 1 х (С • L) , который подается на вход полносвязного слоя D , формирующего отсчет выходного сигнала у _п . Отсчеты у _п могут иметь произвольное значение и различный знак, поэтому для полносвязного слоя используется линейная функция активации.

В настоящее время наиболее популярными рекуррентными ячейками являются простые рекуррентные ячейки (SimpleRNN), Long Short-Term Memory (LSTM) и Gated Recurrent Unit (GRU). Конечно, существует большее количество рекуррентных ячеек. Например, только в работе [7] рассматривается 8 модификаций ячейки LSTM, которые, как показали результаты экспериментов, не дают значительного преимущества перед перечисленными выше архитектурами. Поэтому в архитектуре, представленной на рисунке 2, использовались SimpleRNN, GRU и LSTM ячейки. Число ячеек в слое С в нейронной сети выбиралось из набора 4, 16, 32, 64, 128, 256, число слоев L - от 1 до 4. Выходной полносвязный слой D содержит один нейрон с линейной функцией активации.

Реализация и оценка производительности представленной архитектуры нейронной сети проводилась с помощью библиотеки keras, являющейся частью библиотеки TensorFlow 2.10.0, которая работает под управлением операционных систем Windows и Linux без установки дополнительных виртуальных машин. Для работы с библиотекой использовался интерпретатор python рекомендуемой разработчиком версии 3.10.0. Также дополнительно были установлены библиотеки для ускорения вычислений на графическом процессоре nVidia: cuDNN 8.1 и CUDA 11.2. Использовались стандартные для используемой версии библиотеки keras настройки рекуррентных ячеек, за исключением параметра return_sequences = True , который необходим для реализации указанной архитектуры сети.

' dM x dt	= Y (B o M y — M z B y ) —	M x Т 2 ,
dM y -- dt	= Y (B x M z — M x B o ) —	M,                       (1) T 2
dMz Z < dt	= y ( M x B y — M y B x ) —	M z — M o Т 1     ,

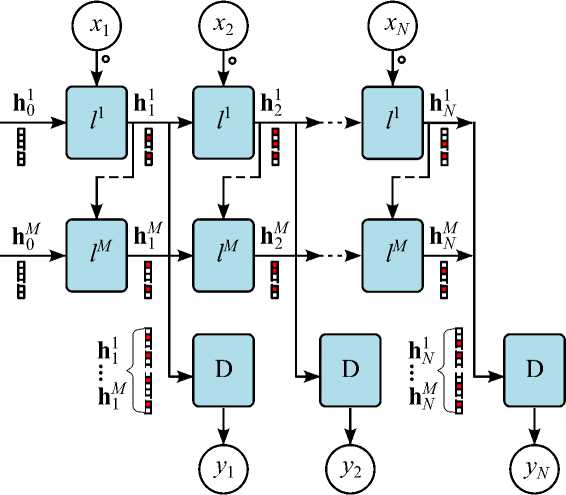
Рис. 2. Архитектура глубокой рекуррентной нейронной сети для синхронного преобразования сигналов

Для обучения нейросетевого эмулятора необходимо подготовить набор тренировочных данных. В представленной работе использовалась аналитическая модель спиновой системы. Динамика намагниченности M (t) гомоядерной системы, находящейся в постоянном магнитном поле B o = B o z и под действием переменного поля B _x (компоненту В _у при этом полагаем равной нулю), описывается уравнениями Блоха [4]:

где y — гиромагнитное отношение (для протонов y = 42,57 МГц/Тл); Т 1 , Т 2 - время продольной и поперечной релаксации соответственно. Причем в экспериментах наблюдается наведенная в катушке ЭДС, пропорциональная одной из поперечных компонент намагниченности.

При обучении сети использовалось множество, содержащее К = 640 пар сигналов: последовательность из двух РЧ-импульсов и отклик на них спиновой системы. Импульсы представлялись в виде дискретной последовательности:

B _x [n] = 2А[п] sin( Y B _o nAt + ф ),

где номер отсчета п = 0,1,... М — 1 ; МAt - длительность импульса, причем параметр М варьировался в пределах от N/10 до N/4 ; параметр N - суммарное количество отсчетов, приходящееся на один импульс и следующего за ним отклика, изменялся в пределах от 200 до 500. Положение переднего фронта первого импульса всегда совпадает с началом воздействия, положение фронта второго импульса выбиралось случайно в пределах от

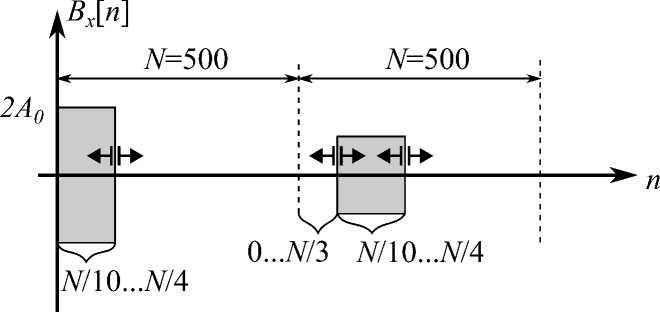
Рис. 3. Параметры импульсной последовательности

0 до N/3 . Время дискретизации At выбиралось из условия, чтобы на период радиочастотного заполнения приходилось 10 отсчетов, то есть At = 10^ . РЧ-импульсы имели прямоугольную огибающую А[п] = А ₀ = const , причем амплитуда выбиралась равновероятно из диапазона А ₀ Е [10 ^-5 ,10 ^-3 ] , а начальная фаза - из диапазона ср Е [ — п , п ] . На рисунке 3 схематично показаны два РЧ-импульса с прямоугольной огибающей и приведены их основные параметры.

Решение системы уравнений Блоха (1) осуществлялось с помощью неявной схемы методом Рунге-Кутты пятого порядка, реализованной в функции solve_ivp библиотеки scipy. Поскольку отклик в реальной системе не может быть получен в момент действия импульса, решение уравнения умножается на «маску», равную 0 во время импульса и 1 – только после его окончания. Пример рассчитанного отклика приведен на рисунке 4.

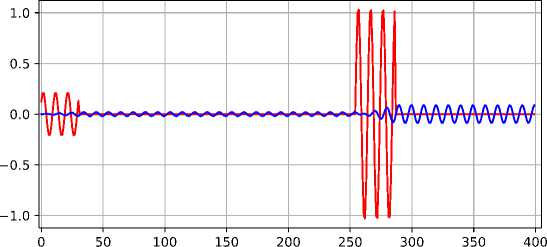
Рис. 4. Пример отклика ( синяя линия ) спиновой системы на импульсное воздействие ( красная линия ) с прямоугольной огибающей

В процессе обучения минимизировалось среднеквадратичное отклонение (СКО) последовательности с выхода сети от целевого отклика спиновой системы на заданное импульсное воздействие. Обучение проводилось в два этапа (по 500 эпох обучения на каждом этапе и размером пакета 64) с помощью адаптивного алгоритма Adam с различной скоростью обучения η. Сначала сеть обучалась с параметром η = 10 ^-3 , а на втором этапе параметр η уменьшался до значения 10 ^-4 .

Тестирование нейросетевой модели осуществлялось на отличном от обучающего множестве. Тестовое множество состояло из К = 64 пар сигналов: последовательность из десяти РЧ-импульсов вида (2) и отклик на них спиновой системы. Количество от- счетов, отведенное на один импульс и последующую релаксацию, в тестовом множестве было выбрано N = 200. Таким образом, общая длительность тестовых сигналов в два раза больше, чем для тренировочных. Остальные параметры были оставлены без изме- нений. Использовались последовательности импульсов как с прямоугольной огибающей, так и в виде гауссова колокола А[п] = 2А1 exp (-100(п-2Т22) ^, ^1 ^ [0,05,1].

Точность предсказания отклика у^ обученной нейронной сети на произвольное за- данное воздействие можно оценить как отношение энергии отклонения откликов к энер- гии истинного отклика ук:

Е _к =

^ ^(у к,п    ^у к,п )

п

Е Ы,п ) ²

2.    Результаты и обсуждение

Проводилось обучение представленной на рисунке 2 архитектуры для различных ячеек (SimpleRNN, GRU и LSTM) по описанному в п. 1 методу. Установлено, что простая рекуррентная сеть SimpleRNN обучается плохо во всех конфигурациях. Относительная энергия отклонения отклика (3) превышает 100 % как на тренировочном, так и на тестовом множествах. К тому же, в используемой версии keras ячейки этого типа плохо оптимизированы, поэтому для одной эпохи обучения требуется больше времени, чем при использовании ячеек GRU или LSTM. Поэтому ниже приведены подробные результаты только для архитектур с ячейками GRU и LSTM.

На рисунке 5 приведены зависимости СКО предсказанных откликов на тренировочном и тестовом множествах от числа слоев L и нейронов в слое С при использовании в архитектуре, показанной на рисунке 2, ячеек LSTM. В процессе обучения СКО не во всех случаях монотонно уменьшается, поэтому на графиках приведены средние по 100 последним эпохам значения.

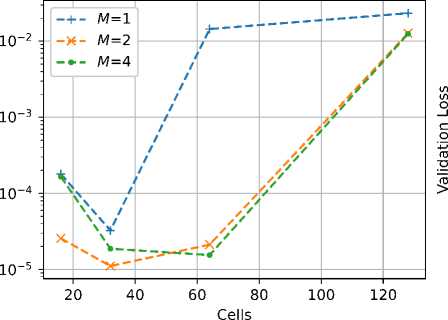
Рис. 5. Зависимости СКО предсказанных откликов нейронной сети с ячейками LSTM на тренировочном ( слева ) и тестовом ( справа ) множествах

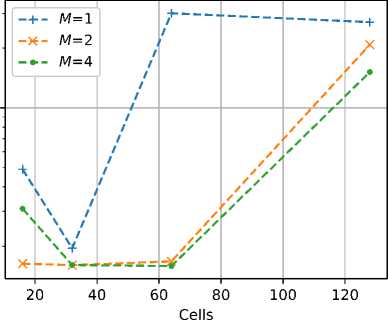
Из приведенных на рисунке 5 зависимостей следует, что наиболее устойчивыми на сравнительно длинных выборках являются конфигурации с малым числом нейронов. Ошибка на тестовом множестве на два порядка превышает ошибку на тренировочном множестве, что свидетельствует о плохой обобщающей способности сети и ее переобучении. В таблице приведены значения рассчитанных по формуле (3) ошибок предсказания отклика для всех сочетаний числа слоев и нейронов в слое. Несмотря на то что максимальное значение ошибки (3) для наиболее удачных конфигураций составляет порядка 10 %, огибающая предсказанного отклика довольно близка к огибающей истинного отклика. Это хорошо видно из рисунка 6, на котором приведены примеры откликов нейронной сети в конфигурации L = 4, С = 64.

О

-1

-2

Best

Input Truth Predicted

о

Рис. 6. Примеры откликов на воздействие в виде последовательности из 10 РЧ импульсов, предсказанных нейронной сетью с ячейками LSTM в конфигурации L = 4, С = 64. Сверху приведены предсказанный и истинный отклики, когда ошибка предсказания (3) максимальна (10,2 %). Снизу показаны зависимости для наилучшего предсказания, ошибка составляет 1,7 %

Средние и максимальные ошибки (на тестовом множестве) предсказания отклика спиновой системы на воздействие в виде десяти РЧ импульсов нейронными сетями на основе ячеек LSTM и GRU

Конф.		LSTM		GRU
L	C	( Е к ) , %	max k { Е к } , %	( Е к ), %	max k { Е к } , %
1	16	16,7	38,8	7,8	30,9
1	32	6,8	13,1	1,4	5,1
1	64	149,7	750,0	4,5	16,7
1	128	109,1	673,8	113,6	784,2
2	16	4,4	9,7	0,5	1,4
2	32	5,2	10,8	0,2	0,7
2	64	4,7	8,8	0,7	2,3
2	128	112,8	615,1	59,4	216,2
4	16	9,7	24,3	0,7	2,1
4	32	4,9	10,9	35,8	105,2
4	64	5,5	10,2	0,2	0,6
4	128	21,9	61,7	97,2	294,0

Основные различия проявляются в предсказании отклика в момент действия импульса. Также установлено, что не совсем корректно предсказывается частота. Это может быть связано с тем, что обучающая выборка короче, чем тестовая. Поэтому была проведена еще одна итерация обучения для набора данных, в котором воздействие пред- ставляет собой 2 импульса, но включающего дополнительные 1 000 точек отклика. Таким образом, длительность откликов в тренировочном наборе составляет 2 000 отсчетов, как и в тестовом. После 10 дополнительных эпох обучения с параметром η = 10-4 максимальная ошибка (3) на тестовом множестве составила 1,1 %, минимальная ошибка 0,1 %. Общее время обучения при использовании графического ускорителя RTX2060 в мобильном исполнении составило менее 30 минут.

Аналогичные эксперименты были проведены при использовании в архитектуре сети ячеек GRU. Из представленных в таблице результатов следует, что в задаче предсказания отклика гомоядерной спиновой системы ячейки GRU, при равных сочетаниях слоев и ячеек в слое, показывают лучшие результаты, чем сети с ячейками LSTM. При этом для сети ячейками GRU не требуется проводить третью итерацию обучения на наборе данных с дополнительными точками отклика. При сравнении кривых обучения для конфигураций L = 2 слоя по С = 32 ячейки установлено, что на втором этапе обучения при использовании параметра η = 10 ^-4 СКО откликов на тестовом множестве для сети с ячейками LSTM остается постоянным на уровне 1,5 • 10 ^-3 , при этом ошибка на тренировочном множестве плавно уменьшается. Это свидетельствует о переобучении сети. При этом СКО откликов для нейронной сети с ячейками GRU на всех этапах обучения и на всех множествах плавно уменьшается. Время, требуемое для проведения двух итераций обучения в конфигурации L = 2 , С = 32 с использованием графического ускорителя RTX2060, составляет порядка 10 минут. По этой причине в рассматриваемой задаче следует использовать нейронную сеть с ячейками GRU.

Заключение

Описанная в работе простая рекуррентная архитектура может быть использована в задачах предсказания отклика нелинейных нестационарных систем, там, где описываемую систему не удается параметризировать, либо число параметров системы оказывается слишком большим. Так, в магниторезонансной спектроскопии можно на простых веществах обучить нейронную сеть адекватно воспроизводить отклик на заданные импульсные последовательности, рассматривая спектрометр и исследуемое вещество как единую систему. А затем, используя обученную модель, подобрать более эффективные последовательности импульсов уже для других веществ, компенсируя неидеальность узлов спектрометра.

Показано, что для корректной работы эмулятора не требуется большого размера обучающего множества, а весь процесс обучения занимает несколько минут на персональном компьютере среднего ценового диапазона.