Нейросетевой подход к мониторингу состояния промышленных роботов-манипуляторов

1Возрастание сложности промышленных роботов-манипуляторов ставит задачу их мониторинга и обнаружения неисправностей в процессе эксплуатации. Несмотря на то, что эта задача рассматривалась рядом авторов [2; 3; 5; 9; 14], в настоящее время нет единого метода, позволяющего решить проблему самодиагностики в полном объеме. Поэтому в данной работе предлагается гибридный подход, объединяющий традиционные статистические модели, а также методы, основанные на принципах искусственного интеллекта.

В настоящее время наибольшее распространение получили методы мониторинга состояния роботов-манипуляторов, основанные на контрольных картах [2], в основе которых лежит предположение, что при отсутствии отказов наблюдаемая величина представляет собой некоррелированный статистический процесс [11]. Однако для большого класса промышленных роботов это предположение нарушается. Кроме того, требуется разработка специальных методов идентификации, робастных к шуму измерений и квантованию входных сигналов.

При анализе контрольных карт проводится статистическая проверка ряда гипотез, позволяющая обнаружить необычные вариации контролируемого параметра робота, обусловленные особыми (неслучайными) причинами. Наиболее часто используются тестовые правила, основанные на выявлении маловероятных «опасных» ситуаций, таких как выход за контрольные границы, тренд, приближение к контрольным границам и т. д. [7]. Однако, как отмечается рядом авторов [6; 12], данный подход не гарантирует отсутствие ошибок. Поэтому проводятся активные исследования по разработке других методов анализа контрольных карт, использующие аппарат экспертных систем, нейронных сетей и эвристические алгоритмы [1; 4; 8; 10; 13], но предложенные в этих работах алгоритмы не учитывают специфику рассматриваемой проблемы.

В данной статье предложен новый нейросетевой метод мониторинга состояния, который позволяет распознать «опасные» ситуации в контрольных картах промышленных роботов-манипуляторов с инкрементальными датчиками перемещения в цепи обратной связи. В отличие от известных подходов, основанных на анализе данных, полученных в результате периодических измерений некоторого контролируемого параметра, предложенный метод анализирует характер изменений параметров динамической модели, которые оцениваются путем идентификации в режиме реального времени.

Динамика исполнительных приводов электромеханических роботов-манипуляторов может быть описана следующими уравнениями:

p ( t ) =^v ( t ) ;

T • V ( t ) + v ( t ) + m • sgn ( v ( t ) ) = k • и ( t ) , (1) где p ( t ) - угол поворота вала двигателя (выходная переменная); ν( t ) – скорость вращения вала; u ( t ) - управляющее воздействие; к - коэффициент передачи; T - электромеханическая постоянная времени; m - амплитуда возмущающего воздействия. Следует отметить, что в этой модели параметры T и m рассматриваются как основные характеристики состояния объекта, которые далее используются при мониторинге. Дискретизация исходной модели (1) по времени приводит к следующим выражениям:

^v k +1 = н ^v _k ^{+ (1-} н⁾⁽ ku k ^- m );

^V k = (Р к +1 ^{- 2} Р к ⁺ Р к -1 ^{)/2 Т} 0 , ⁽²⁾ где н = ехр(- T ₀/ Т); T 0 - период квантования по времени. Для идентификации параметров модели первоначально предположим, что коэффициент передачи к и скорость вала v _к могут быть оценены с достаточной точностью. Тогда основное уравнение для идентификации может быть записано в виде

А_k + m = ( B_k + m )μ;

А_k = ν_{k +1} – ku_k ; B_k = ν_k – ku_k .          (3)

Определим критерий качества следующим образом:

F ( ц , m ) = 2 [ ( А ^{+ m} )^-( ^в к ⁺ m ) -ц] ² .   ⁽⁴⁾

к = 1

Приравнивая производные функции F ( ц, m ) к нулю и решая соответствующую систему уравнений, получаем выражения для расчета параметров ( ц, m ):

n    nn

П 2 А к В к - 2 А к 2 В к

_ к = 1 ____________ к = 1 к = 1     .

^ц                    к       X 2 ^;

nn n2(Вк)2 - 2Вк к=1           V к=1 7

nn ц2 Вк-2 Ак m = к=1______к =1

n ( 1 -ц )

где n - размер выборки. Если коэффициент передачи k неизвестен, то динамическая модель (2) может быть представлена как линейная регрессия вида ν_{k +1} = а ν_k + bu_k + c , где а = μ; b = (1 - н) к ; с = -(1 - н) m и соответствующая задача идентификации может быть ре-

шена с использованием псевдоинверсии Мура-Пенроуза:

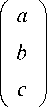
f 2 v 2 ^к

2 v_k и к

2 v_k

V к

2 v_k и к

к

2 и к

к

2 и к

к

2 v k

к

2 и к

N

2 ^vk + 1 ^vk к

2 V k + 1 и_к k

. (6)

2 V k + 1

V к 7

Тогда искомые параметры модели вычисляются на основе следующих выражений:

μ = а ; m = – c /(1 – а ); k = b /(1 – а ).    (7)

Однако проведенные исследования показали, что это выражение менее робастно к шуму измерений по сравнению с выражением (5). Поэтому целесообразно разбить иден-

Havko-

ЖГРАДА

тификационную процедуру на два шага. На первом шаге производится оценка коэффициента передачи (в установившемся режиме), а на втором осуществляется идентификация параметров T и m , которые необходимы для мониторинга состояния и диагностики отказов робота.

Чтобы использовать выражения (5) и (7) для идентификации, требуется массив скоростей и соответствующих управляющих воздействий {vk, uk | k = 1:n}. Однако рассматриваемые промышленные роботы-манипуляторы оснащены инкрементальными датчиками, которые позволяют получить только код положения. Поэтому скорость должна оцениваться численно. Очевидно, что простейшая оценка скорости v i ¹ = ( p_{t + 1} - P i ) ,T₀ является очень чувствительной к шуму квантования. Чтобы показать это, предположим, что ошибка измерений описывается белым шумом с нулевым математическим ожиданием и дисперсией а². Тогда среднеквадратическое отклонение оценки скорости имеет вид 5[ v ⁽¹⁾ J = а V2/ T ₀ , причем а ² = а 1 + а ₂², где _а 1 = д/ 712 обусловлено погрешностями квантования по уровню с шагом Д , а а ₂ = v _max • T 0 /V12 учитывает погрешности квантования по времени при максимальной скорости v_max. Соответствующие вычисления при типичных значениях Δ = 2π/1024 и v_max = 10 inc / tic дают 5^ v ⁽¹⁾ J Jv _max » 40 % (рис. 1), поэтому для идентификации параметров динамической модели должны использоваться более точные оценки скорости.

Чтобы повысить точность вычисле-

где

Spt = E Pk k V

^ r

- n E Pk • kk k 7 V

)

^- n E t k ;

k 7

-                   2

s. = E tk -nУл tt            k               k

k V k 7

ния скорости, применим метод скользящего окна для интервала времени [ t - LT ₀; t + LT ₀]. Простейшее выражение такого типа v i² = ( P i _{+ L} — Pi. - _L )/ 2 LT₀ использует граничные значения выходной координаты p ( t ) и дает ошибку 5[ v ⁽²⁾l = o V2/2 LT₀ . Дальнейшее снижение ошибки может быть достигнуто при использовании линейного сплайна, обеспечивающего сглаживание p ( t ):

v ⁽³⁾ = arg min E [ a + vt i - P i ] ². (8)

Дифференцируя это выражение по параметрам a и v и решая соответствующие уравнения, получим

v( 3)

= S pt (S tt

Далее предположим, что p ( t ) = ν t + х, где x - белый шум с параметрами (0, s), и ра ссмотрим скользящее окно t е [ - LT₀ ; LT₀ ] . Тогда эти суммы равны:

LL

S Pt = vT 0² • ! i ² + T 0 • ! i ^ i , i =— L          i =— L

L

S .t = T 0² • £ i ² ,                (^|0)

i=—L и искомая оценка скорости может быть представлена как

L

v ^{( 3 )} = v + 3 E i ^ i T₀ ( 2 L ³ + 3 L ² + L ) . (11) i =— L

Очевидно, что среднеквадратическое отклонение v(3) рассчитывается следующим образом:

5 [ v ⁽³⁾ J = а/ vT ₀ V 2 L ³ + 3 L ² + L ,        (12)

и существенно ниже, чем для оценок ν⁽¹⁾, ν⁽³⁾. Как показали экспериментальные исследования (рис. 2), необходимая для рассм а триваемых приложений точность δ[ν⁽³⁾] ≤ 0,004 достигается для скользящего окна с параметром L = 20.

Для обнаружения отклонений в динамическом поведении промышленного робота-манипулятора используем контрольные карты типа X , R , S , которые, как показал проведенный анализ, позволяют достичь наилучшей достоверности при мониторинге состояния робота. При этом разделим диапазон изменения анализируемых параметров T , m на три равные зоны ( A , B , C ) и применим 10 правил, нарушение которых в режиме нормальной эксплуатации маловероятно. К числу этих правил относятся: «Выход за контрольные границы», «Выход ниже/выше центральной линии» (7 из 7, 10 из 11, 12 из 14, и 14 из 16 точек), «Попадание в зону С » (15 из 15 точек), «Избежание зоны С » (4 из 5 точек), «Точки в зоне А или вне зоны А » (2 из 3 точек), «Линейный тренд» (7 точек), «Колебательный тренд». При этом для снижения вероятности

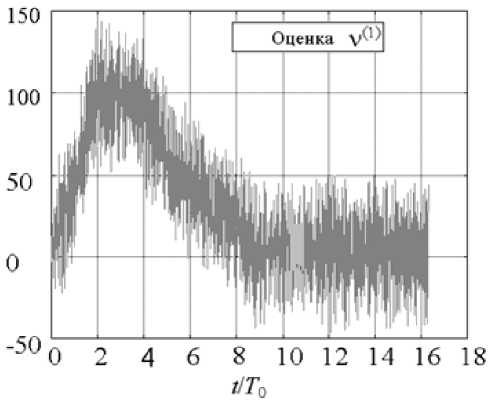
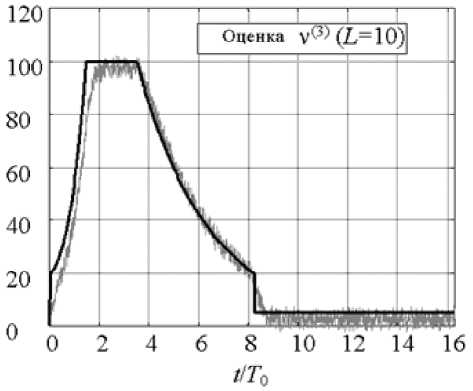
Рис. 1. Сравнение методов оценки скорости

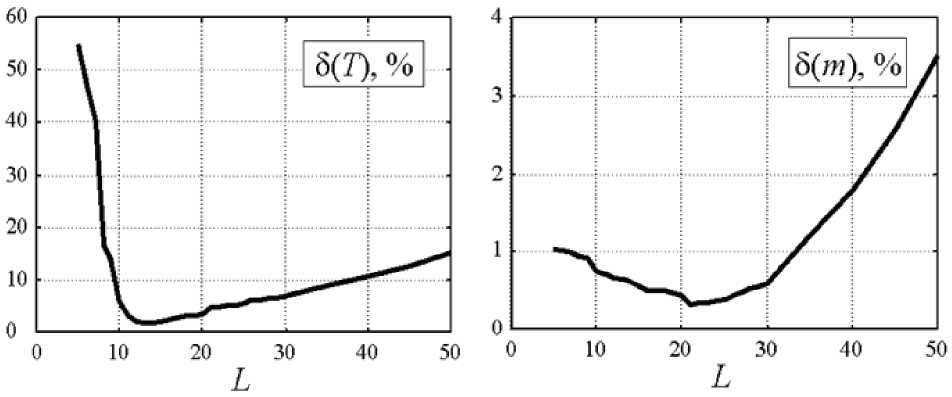
Рис. 2. Ошибки оценок δ ( T ) и δ ( m ) для разных значений L

ошибок диагностики названные правила применяются совместно.

Для дальнейшего повышения достоверности мониторинга используем нейронную сеть обратного распространения (FFN), которая позволяет описать существенно нелинейные соотношения между входным и выходным сигналами. Предложенная модификация FFN-сети (рис. 4) представляет собой четырехслойную структуру, содержащую 21 нейрон во входном слое. Этот слой используется для ввода данных от контрольных карт (20 последовательных точек и математическое ожидание М). Выходной слой сети состоит из одного нейрона, а его выход принимает значения 1 или 0 (соответственно для нормального и аварийного состояния робота-манипулятора). Два скрытых слоя сети содержат 40 и 60 нейронов соответственно. Для активации нейронов в скрытых и выходном слоях используется функция гиперболического тангенса. Для генерации требуемого для обучения сети множества контрольных карт использован метод Монте-Карло.

Для обучения сети применялся алгоритм обратного распространения с параметром скорости обучения 0,5. В процессе обучения весовые коэффициенты настраивались таким образом, чтобы минимизировать среднеквадратичную ошибку ( MSE) между вектором состояния сети и обучающим множеством. Для обучения было сгенерировано 3800 наборов данных (1000 для нормального функционирования робота и 2800 для различных типов аварийных ситуаций). Веса нейронной сети модифицируются до тех пор, пока не выполнятся условия £ <  £ _max or i <  i _max, где £ - значение MSE , i – количество итераций.

В процессе исследования рассмотрен ряд четырехслойных сетей обратного распространения, отличающихся значениями размерности скрытых слоев h ₁ и h ₂, а обучение

Havko-

ЖГРАДА

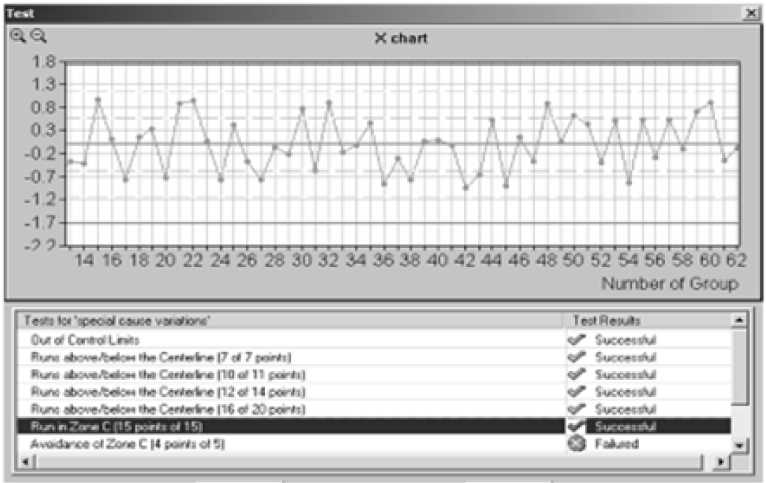
Рис. 3. Пример анализа данных идентификации

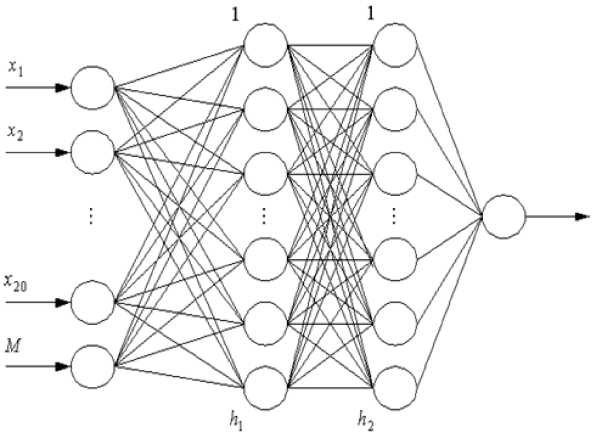
Рис. 4. Нейронная сеть для анализа контрольных карт

проводилось до достижения значений £max = = 10-5 или imax = 3000. Графики изменения MSE в процессе обучения для сетей с различной размерностью скрытого слоя приведены на рис. 5 (моделирование проведено в пакете MatLab). Для тестирования этих сетей использовано 140 наборов данных для аварийных режимов и 50 наборов данных для режима нормального функционирования. Результаты обучения и тестирования сетей приведены в табл. 1 (значения достигнутых в процессе обучения ошибок (MSE) и процент корректно распознанных ситуаций на тестовом множестве Р). Моделирование показало, что минимальное значение £ = 0,00015 достигается при размерности скрытых слоев h1 = 50 и h2= 40. Однако, как следует из табл. 1, для случая h1 = 60 и h2 = = 40 получено большее число корректно распознанных ситуаций (94 %), поэтому сеть с такими параметрами применена для диагностики состояния манипуляционного робота в промышленной робототехнической системе, которая включает 5 подвесных манипуляторов, которые обслуживают 200 рабочих станций.

Предложенный метод мониторинга состояния электромеханических роботов-манипуляторов с инкрементальными датчиками обратной связи, основанный на анализе параметров динамической модели при помощи нейронной сети типа FFN, позволяет повысить достоверность обнаружения отказов. На основе предложенного метода разработан

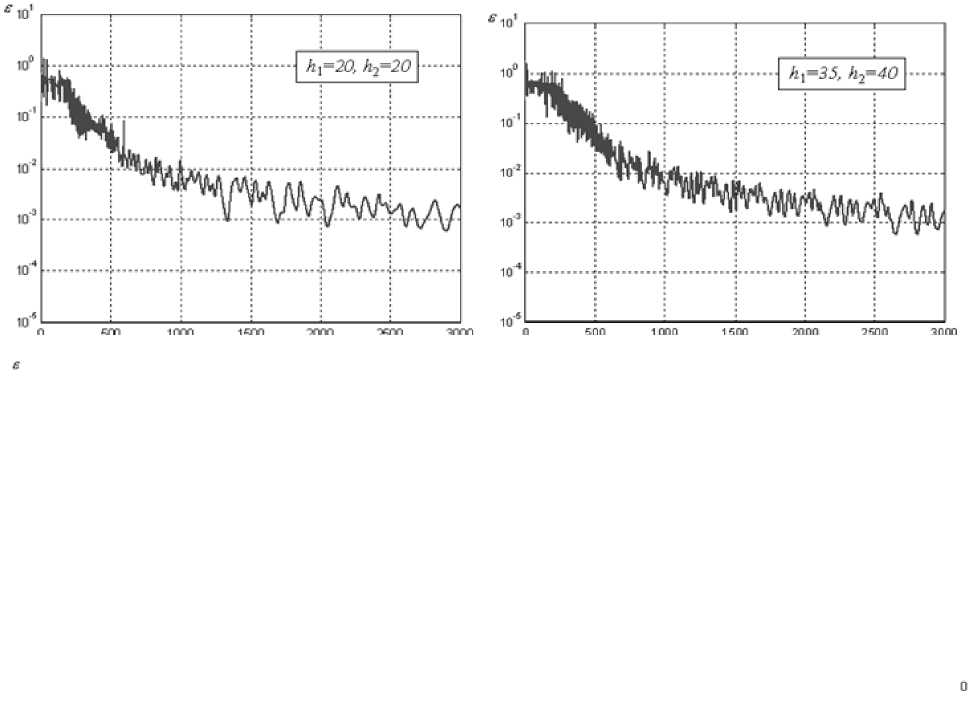
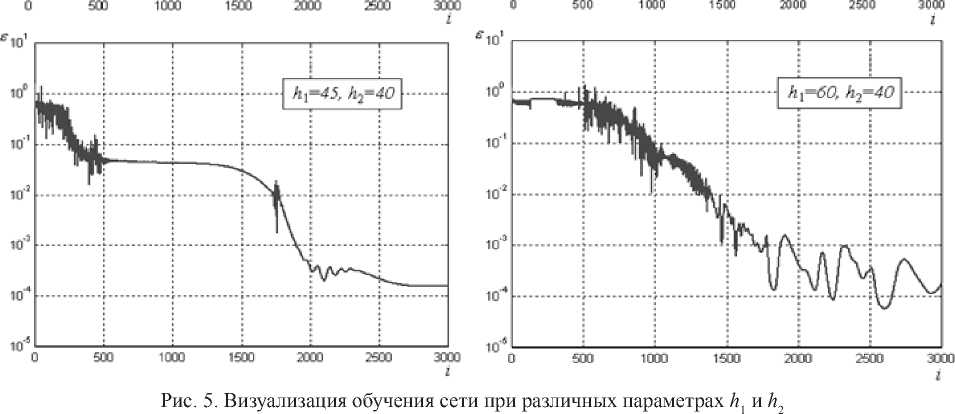
Таблица 1

Результаты обучения нейронных сетей

h 1 h2 ε Время обучения, с P, % 20 20 0.00162 300 89.5 25 25 0.000132 330 87.5 30 30 0.00035 408 91.6 35 40 0.00175 420 90.0 40 40 0.00052 480 91.1 45 40 0.00015 510 93.6 50 40 0.00015 528 93.7 60 40 0.00018 600 94.0 программный модуль, эффективность которого подтверждается примерами практического применения при мониторинге состояния промышленной робототехнической системы.