Нейросетевой подход к реализации агента анализа подсистемы балансировки TriadBalance

Появление современных высокопроизводительных вычислительных систем позволяет в значительной мере оптимизировать время выполнения имитационного эксперимента за счет перераспределения вычислений на различные процессоры (в многопроцессорной ЭВМ) или рабочие станции в сети. В связи с этим актуально появление программных систем имитационного моделирования, которые позволяют выполнять распределенный имитационный эксперимент [1, 2, 3, 4]. Однако разработчики распределенных систем имитации сталкиваются с проблемой дисбаланса нагрузки [5]. Зачастую с помощью алгоритмов динамической балансировки можно достичь эффекта только для конкретных распределенных имитационных моделей или для конкретного алгоритма синхронизации[6, 7]. В системе имитационного моделирования Tri-ad.Net предпринята попытка разработать управляемый алгоритм балансировки, действующий по правилам, в которых учитываются характерные особенности конкретной имитационной модели, конкретной вычислительной системы, на которой проводится имитационный прогон [8]. В настоящее время ведутся работы по созданию мультиагентной подсистемы балансировки TriadBalance [9, 10], выполняющей децентрализованный сбор статистических данных о функционировании ими-

тационной модели и вычислительной системы, с помощью агентов-датчиков определяющей момент возникновения дисбаланса (агент анализа), оптимальное перераспределение нагрузки на вычислительных узлах (агент распределения), перенос нагрузки (агент миграции). Цель, которую преследуют исследователи при разработке мультиагентной системы балансировки, – достичь высокой адаптируемости алгоритма балансировки к различным ситуациям (различные модели, различные алгоритмы синхронизации распределенных объектов имитационной модели). Предлагаем использовать нейросетевой подход при разработке агентов, реализующих алгоритм динамической балансировки. Ниже рассматривается опыт разработки агента анализа в мультиагентной подсистеме балансировки.

1.    Постановка задачи перед агентом анализа

Подсистема балансировки TriadBalance в составе распределенной системы имитационного моделирования Triad.Net, как уже упоминалось ранее, построена как мультиа-гентная система. Связующим звеном между агентом статистики, собирающим данные о работе узлов в имитационной модели, и агентом распределения, занимающимся непосредственно перераспределением вычислительной нагрузки между узлами, является агент анализа. В его обязанности входит выявить дисбаланс, возникший в системе.

Архитектура системы TraidBalance представлена на рис. 1.

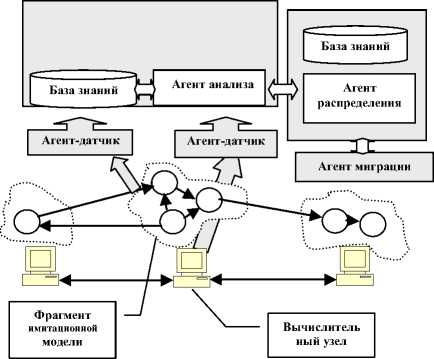
Рис. 1. Архитектура системы TriadBalance

Агент анализа сообщается непосредственно с двумя агентами: агентом сбора статистики и агентом миграции или перераспределения.

Агент анализа сообщается с агентом статистики через механизм доски объявлений. Информация на ней хранится в строго определенном формате. Агент статистики через определенные промежутки времени корректирует данные на доске, после чего агент анализа может извлекать из нее информацию.

На доску достаточно помещать не всю доступную информацию, а лишь обобщенные характеристики, дающие представление о характере загруженности каналов и процессоров за последнее время.

Будем понимать под дисбалансом в вычислительной системе перегруженность одного или нескольких процессоров или достижение максимума пропускной способности одного или нескольких каналов связи. Чтобы избавиться от дисбаланса в вычислительной системе, нужно либо нарастить вычислительные мощности, либо обратиться к более экономичному и рациональному способу их использования.

Подсистема обнаружения дисбаланса с необходимостью задействует те вычислительные мощности, работу которых должна оптимизировать, поэтому крайне важно, чтобы сама подсистема была нетребовательна к ресурсам и работала максимально эффективно.

Таким образом, агент анализа должен отвечать всем вышеуказанным требованиям.

• 2.    Необходимость разработки собственной основы для агента анализа

• 3.    Преимущества использования нейронных сетей для решения задачи балансировки

Большинство решений, призванных обеспечить равномерность загрузки вычислительных мощностей, строятся исходя из особенностей постановки задачи, или они подходят только для ограниченного класса систем. Более того, такие решения зачастую носят закрытый характер, а потому недоступны для внесения изменений и дополнений. Этим объясняется необходимость разработки отдельного решения задачи балансировки и агента анализа как составной части этого решения для подсистемы TriadBalance.

Важно отметить, что требования к конкретной системе балансировки прямо влияют на выбор подхода к ее реализации. В качестве альтернатив использованию нейронных сетей для задачи определения дисбаланса загрузки мощностей в вычислительной системе могут быть предложены деревья решений, экспертные системы, продукционные системы, алгоритмический метод. Отметим, что каждый из указанных классов подходов применим для данной задачи, однако имеет свои преимущества и свои недостатки.

Продукционные системы использованы при реализации алгоритма динамической балансировки и описаны в работе [9]. Несколько иной подход изложен в работе [12]. Здесь для реализации динамической балансировки используется мультиагентный подход, нейронные сети (распознавание дисбаланса) и генетические алгоритмы для подбора характеристик нейронной сети. В работе [11] предложена архитектура подсистемы TriadBalance c использованием агентов, обученных на нейронной сети.

Кратко рассмотрим особенности задачи поиска дисбаланса с точки зрения предложенных альтернатив.

Исходные данные в задаче – действительные и целые числа. Большой объем числовых данных делает применение экспертных систем, основанных на работе с символьной информацией, затруднительным.

Одним из принципиальных преимуществ нейронных сетей для решения задачи определения дисбаланса является их способность настраиваться на особенности конкретной системы и, что не менее важно, на сложившуюся в ней ситуацию в конкретный момент времени.

Характер и способ использования ресурсов в нетривиальной системе заранее предсказать очень сложно, однако возможно предвидеть закономерности, которые должны быть в реально действующей системе. К таким закономерностям можно отнести, например, резкое сокращение ресурсов (как каналов, так и вычислительных мощностей) ночью, по сравнению с загрузкой в дневное время суток.

Однако все такие ситуации и возможные изменения поступающей нагрузки на узлы вычислительной системы заранее предусмотреть практически невозможно.

Неравномерный характер работы вычислительной системы обусловливает предпочтительное применение тех методов, которые способны распознавать, в каком режиме работает система, и, возможно, классифицировать ее характеристики на основе наблюдений о работе системы, полученных в предыдущие моменты времени.

Благодаря своей способности выявлять закономерности, не очевидные человеку, и приобретать их нейронная сеть имеет преимущества перед другими средствами, а именно: нейронная сеть может обучаться и дообучаться по одним алгоритмам, достаточно лишь добавлять в обучающую выборку новые входные примеры. В частности, значительные проблемы с донастройкой на изменившиеся условия имеют продукционные системы. Если правила не внесены экспертом в продукционную систему до начала ее применения, то трудно внести (через, например, использование метазнаний) адекватные изменившимся условиям правила по ходу работы.

Слабым местом всех экспертных систем является достижение согласованности мнений экспертов, а также трудоемкость работы по выявлению закономерностей и значительность затрат по оплачиванию такой работы.

Достоинством экспертных систем, равно как и деревьев решений, перед нейросетями являются большие способности по объяснению принятого решения. Однако в системах балансировки наличие объяснения решения менее ценно, чем качество найденного реше- ния, так как зачастую объяснение требуется лишь для отладки и настройки системы, большую же часть времени алгоритмы балансировки работают без вмешательства человека.

Результатом проведенного анализа стал выбор нейронных сетей как наиболее адекватное средство решения задачи поиска дисбаланса.

4.    Результаты применения нейронных сетей

В рамках проведенной работы было разработано программное средство для выбора наиболее подходящего типа нейронной сети, решающего задачу выявления дисбаланса в ВС (вычислительной системе).

В качестве основы были взяты следующие типы сетей: многослойный персептрон, сеть Хэмминга и сеть Кохонена.

Рассмотрим особенности и преимущества использования этих сетей.

Персептрон подходит для решения большого класса задач. В данной работе он был использован потому, что эффективность его подтверждена множеством практических примеров в различных предметных областях [13, 14].

Сеть Кохонена хорошо зарекомендовала себя для решения задач кластеризации в случае, когда количество классов заранее неизвестно [13]. В данной задаче применение этой сети возможно и для первичного разбиения всего множества ситуаций в системе на некоторые подклассы с целью дальнейшего подбора нейронной сети оптимальной структуры для каждого из подклассов в отдельности. Например, работа вычислительной сети может различаться в дневное время (много пользователей, частые запросы) и в ночное время (мало сообщений в сети). В другом случае данная сеть может быть применена для отнесения входного вектора к классу порожденных векторов в большой, средней или малой по объему вычислительной сети.

Сеть Кохонена способная выдавать прямой ответ о наличии или отсутствии дисбаланса, т. е. решать задачу классификации. Была выявлена закономерность, по которой векторы, характеризующие состояние одной вычислительной сети, относятся к одному и тому же классу. Тогда логично предположить, что если новый вектор попадает в класс, где большинство векторов указывают на определенный тип дисбаланса, то и данный вектор указывает на тот же тип дисбаланса. Однако на практике такое предположение не подтвердилось.

Особенность сети Хэмминга в том, что ей изначально требуется некоторое количество классов. Для этого ей также необходим эталонный вектор-образец, который можно интерпретировать как центр данного класса или кластера.

По типу решаемая задача ближе всего к задаче классификации. Все множество состояний вычислительной сети делится на 3 подмножества: дисбаланс, связанный с перегруженностью некоторых каналов, дисбаланс, связанный с перегруженностью некоторых процессоров, и ситуации, при которых дисбаланса нет. В ходе работы нейронной сети ситуация в вычислительной сети должна быть отнесена к одному из этих подмножеств.

Используя суммарную ошибку нейронной сети, можно построить график (см. рис.2), отражающий степень приспособленности того или иного типа сети для решения задачи.

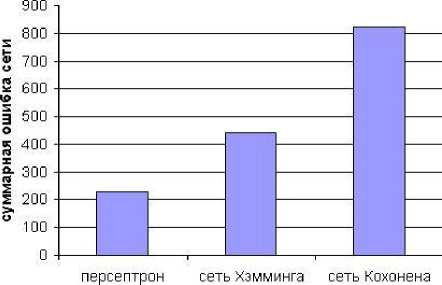
тип сети

Рис. 2. Способность типов сетей решать задачу

Сравнение проводилось после одного прохода по тестовой выборке, количество тестов порядка 3000.

Выводы по применению сети Кохонена

Наименьшую приспособленность показала сеть Кохонена, которая, вообще говоря, свободна от задания принципа классификации. В данном случае ей могут быть выделены классы по более глубоким закономерностям, а не только по наличию дисбаланса какого-либо типа. Можно сказать, что в худшем варианте (вариант реализации агента анализа с помощью сети Кохонена) сеть ошибается в 1 случае из 4.

Выводы по применению сети Хэмминга

Самую большую сложность в применении сети Хэмминга для данной задачи представлял выбор векторов-образцов. Векторы-образцы должны не только быть похожи на все элементы, имеющие одно и то же выходное значение для нейронной сети, но и отличаться от других элементов.

Анализ суммарной ошибки в сети Хэмминга показывает, что векторы, на которых агент анализа должен показывать одно и то же значение дисбаланса, не обладают очевидными сходствами. Следовательно, между компонентами входного вектора существует более глубокая зависимость.

Кроме того, отрицательным свойством сети Хэмминга является неприменимость к ней методики обучения. То есть единственный способ понизить значение функции приспособленности для данной сети – использование генетического алгоритма. Это отличает сеть Хэмминга от персептрона и сети Кохонена.

Более перспективным является применение персептрона для решения поставленной задачи. Однако подбор весов отдельно взятого персептрона, который бы дал оптимальное решение на всех возможных архитектурах вычислительных сетей, крайне сложная задача.

Было принято решение использовать пул, или совокупность нейронных сетей, каждая из которых будет обучаться на некоторой выборке примеров, но характеристики (количество слоев, количество нейронов на слое, тип функции активации и т.д.) для каждой сети из пула будут задаваться изначально. В качества развития идеи была реализована возможность получения из двух данных сетей одного типа (но, возможно, с разными характеристиками) новой сети такого же типа. Таким образом, становится возможным этап скрещивания.

Применение генетического алгоритма

При исследовании проблемы выявления дисбалансов выяснилось, что от топологии нейронной сети в большой мере зависит эффективность решения задачи. Для подбора наиболее подходящих параметров нейронной сети (функции активации, порядка прохода по обучающей выборке, количества нейронов) был разработан и реализован генетический алгоритм. Его применение позволило автома- тизировать процесс подбора параметров нейронной сети.

Генетический алгоритм (ГА) часто используется для решения задач оптимизации и подбора оптимальной структуры нейронной сети [15, 16]. С помощью его возможны поиск и нахождение решений даже в случае неаналитического задания контрольной или фитнесс-функции.

Отметим, что для разных типов сети (сеть Кохонена, Хэмминга или персептрон) необходимо разрабатывать свои процедуры скрещивания, а также подбирать лучшие особи с помощью ГА для каждого типа.

Оптимальным действием при отборе лучших особей в популяции (пуле сетей) стало отбрасывание 5% наименее приспособленных особей популяции после каждого шага ГА.

В качестве значения фитнесс-функции логично выбрать суммарную ошибку нейронной сети на всем множестве тестовых примеров.

Выше показано, что наименьшую суммарную ошибку на всей обучающей выборке среди рассмотренных типов сетей дает персептрон. Процедура поиска наиболее подходящих характеристик для персептрона выглядит следующим образом. Всего было выполнено 40 шагов. Изначальная популяция содержала 162 особи (18 возможных значений количества нейронов на скрытом слое, 3 варианта коэффициента скорости обучения, 3 варианта изменения скорости обучения). Количество особей, удаляемых на первом шаге, равно 17. Параметры генетического алгоритма были настроены таким образом, чтобы после этой процедуры в популяции осталось 9 особей.

Выводы по использованию персептрона

Персептрон зарекомендовал себя как хорошая основа для построения агента анализа. Он хорошо подходит для решения поставленной задачи. Кроме того, был построен генетический алгоритм определения наиболее подходящих характеристик персептрона.

Проведен ряд испытаний (10 испытаний), в ходе которых генетический алгоритм был настроен таким образом, чтобы в результате оставались 9 наиболее приспособленных особей, каждая из которых представляет собой нейронную сеть. При этом можно объединить полученные результаты и рассматривать их совместно, т. е. считать, что генетический алгоритм отобрал сразу 90 особей.

Если проанализировать частотные характеристики выбора генетическим алгоритмом особи с определенной структурой, то получим, что чаще всего (в 71% случаев) выбирался персептрон с коэффициентом скорости обучения 0.05. Скорость обучения равная 0.1 выбиралась в 25% случаев, третий вариант – 0.02 в 4% случаев.

Способ изменения коэффициента обучения теперь есть смысл определять только для варианта, когда была выбрана скорость обучения 0.05. Уменьшение коэффициента после прохода по тестовой выборке на 2% было выбрано в 47% случаев, уменьшение на 1% – в 28% случаев, и уменьшение на 5% – в 25% случаев.

Распределение количества нейронов в полученных особях отражено на рис. 3.

Кол-во попаданий в число лучших особей

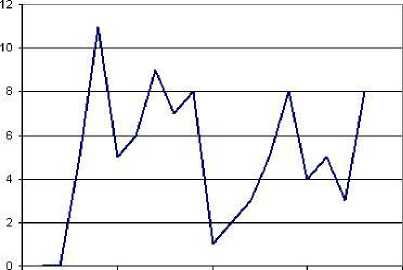
О              5              10             1S             20

кол-во нейронов в скрытом слое

Рис. 3. Зависимость попадания в число лучших особей от числа нейронов в скрытом слое сети

Заметим также, что для количества нейронов больше 9 значения функции приспособленности были в среднем выше, чем ее значения для меньшего числа нейронов.

Отметим длительность времени выполнения генетического алгоритма для персептрона с заданными ранее параметрами. Это время – порядка минуты, оно получено на компьютере со следующими характеристиками:

• •    процессор с тактовой частотой 1,86 ГГц;

• •    ОЗУ 2 Гб;

• •    ОС Windows Vista.

Однако в рабочем режиме персептрона генетический алгоритм не участвует и нейронная сеть с уже подобранными характеристиками будет выдавать ответ почти мгновенно.

Таким образом, результаты использования программы показали, что лучше всего решает задачу агента анализа персептрон с такими характеристиками: число нейронов в скрытом слое равно 4, коэффициент обучения равен 0.05, и он уменьшается на 2% после каждого обучения, количество проходов по обучающей выборке равно 40. Порядок прохода по тестовой выборке последовательный, однако за один шаг обучение проводится только на одной третьей части всей обучающей выборки.

Если количество элементов в тестовой выборке порядка 1000, то суммарная ошибка, которую дает наиболее приспособленная особь, взятая в качестве основы для реализации агента анализа, равна 30–40. То есть в среднем агент анализа дает ошибку не более 0.05 при множестве возможных его ответов {0, 1, 2}. То есть можно считать, что построенный агент анализа хорошо решает задачу распознавания дисбалансов.

В итоге работы была спроектирована и реализована программа, которая подбирает на основе генетического алгоритма оптимальную в некотором смысле структуру нейронной сети для решения задачи выявления дисбаланса в вычислительной системе, а именно оптимальную структуру с точки зрения минимизации ошибки при определении наличия дисбаланса.

Замечания по применению генетического алгоритма

Процедура выбора лучшей конфигурации нейронной сети занимает продолжительное время. Это связано с необходимостью обучения большого количества сетей. Количество тестов в обучающей выборке составляет несколько тысяч, и, даже если за один проход обучать каждую сеть не на всех примерах, время работы генетического алгоритма оказывается большим.

Для сокращения времени подбора лучшей конфигурации нейронной сети можно использовать следующие приемы. С самого начала попытаться убрать как можно больше неприспособленных особей. Например, убирать по 10% популяции нейронных сетей после каждого обучения всех имеющихся на данный момент в популяции сетей, пока число особей в популяции не станет приемлемым (пока обучение всех сетей не будет занимать меньше секунды процессорного времени).

Другой вариант – сокращение пространства поиска наиболее подходящей конфигурации нейронной сети. Для этого сокра- щается количество вариантов каждого из подбираемых параметров в нейронной сети. Например, возможное количество нейронов в скрытом слое выбрать не от 1 до 18, а от 10 до 14, если предварительный анализ показал бесперспективность применения малого количества нейронов в слое.

5.    Направления дальнейших исследований и разработок

Одним из направлений дальнейшей разработки можно назвать интерпретацию причин возникновения дисбаланса, другими словами, контрастирование нейронной сети. Данная проблема является сложной в силу отсутствия общеприменимых приемов вербализации знаний, которым обучилась нейронная сеть, т.е. объяснение причин, по которым нейронная сеть делает то или иное заключение.

Важным представляется научиться прогнозировать возникновение дисбалансов. Если выявление дисбаланса относится к задачам классификации и вполне адекватным оказалось применение нейронных сетей классификационного типа (сетей Кохонена, Хэмминга), то прогнозирование, скорее всего, потребует других методов решения. Возможно, для прогнозирования окажется более целесообразным применение системы, базирующейся на знаниях.

В дальнейшем планируется также тестирование агента анализа на вычислительных сетях большого размера и введение дополнительных характеристик в модель генерации архитектуры вычислительной сети и потоков сообщений в ней, например учет емкости памяти вычислительного устройства и времени на обслуживание запроса к нему, а также генерации сообщений через промежутки времени, распределенные по некоторому закону.

Заключение

В статье рассмотрен вопрос о возможности и целесообразности применения нейросетевого подхода к решению задачи выявления дисбаланса нагрузки в вычислительной сети. Эта задача возлагается на агента анализа, который входит в состав мультиагентной подсистемы балансировки TriadBalance. Подсистема балансировки является одним из компонентов комплекса программных средств, обеспечивающих эффективное проведение распределенного имитационного экс- перимента (система распределенного имитационного моделирования Triad.Net).

Исследования показали эффективность применения многослойного персептрона для реализации агента анализа, выявляющего возникновение дисбаланса. Наряду с многослойным персептроном были проанализированы такие типы сетей, как сети Кохонена и сети Хемминга. Проведенные нами исследования дают возможность выработать практические рекомендации для реализации агента анализа на основе нейронных сетей.

В дальнейшем предполагается провести эксперименты по сравнению подсистемы балансировки, реализованной с помощью агентов, основанных на продукционных правилах, с подсистемой балансировки, в которой используются агенты, обученные на нейронных сетях.