Нейтронные звезды в теории гравитации с неминимальной кинетической связью скалярного поля и кривизны с реалистичными уравнениями состояния вещества

Теория гравитации Хорндески - скалярно-тензорная теория гравитации наиболее общего вида, уравнения движения которой являются дифференциальными уравнениями второго порядка [1]. Одним из подклассов этой теории является так называемая теория гравитации с неминимальной кинетической связью скалярного поля и кривизны. Изначально эта модель расматривалась в связи с различными космологическими сценариями [2]. Следующим шагом в изучении этой модели является рассмотрение звезд и черных дыр, обзор работ по этой теме можно найти в статье [3]. Например, решения, описывающие черные дыры в данной модели, имеют асимптотику анти-де

• ¹    E-mail: pkashargin@mail.ru

• ²    E-mail: lebedev.aleks 2012konnor@yandex.ru

• ³    E-mail: sergey_sushkov@mail.ru

Ситтера, так как неминимальная кинетическая связь скалярного поля и тензора Эйнштейна проявляет себя в качестве отрицательной космологической постоянной [4].

Другим классом компактных объектов являются нейтронные звезды. Из наблюдений установлено, что большинство нейтронных звезд имеет массы 1.2 — 2 масс Солнца M_sun и радиусы 9.9 —11.2 км, однако имеются данные о более массивных звездах с массами достигающими 2.7 M_Sun- Плотность в центре такой звезды в несколько раз превышает ядериую р^ 心 2.5x10¹⁴r см^-3. Сферически симметричные нейтронные звезды рассматривались в теории гравитации с неминимальной кинетической связью скалярного поля и кривизны в случае, когда действие не содержит кинетический член скалярного поля 印 =0, а «голая» космологическая постоянная равна нулю Ло = 0 [5]. В дальнейшем этот результат был расширен. В работе [6] были рассмотрены медленно вращающиеся нейтронные звезды с реалистичными уравнениями состояния нейтронного вещества. В работе [7] были рассмотрены сферически симметричные нейтронные звезды в случае ненулевых параметров £i и Ло, а в качестве уравнения состояния было взято простейшее уравнение политропы.

В данной работе мы рассматриваем нейтронные звезды в теории гравитации с неминимальной кинетической связью скалярного поля и кривизны, описываемой действием (1) в случае ненулевых значений параметров £1,2, I и космологической постоянной Ло, материя которых описывается реалистичными уравнениями состояния вещества. В качестве уравнений состояния были использованы аналитические представления унифицированных уравнений состояния холодного ядерного вещества BSkl9, BSk20, BSk21 (функционалы Брюссель - Монреаль - Скерми) [8]. В §1 мы кратко рассмотрим теорию гравитации с неминимальной кинетической связью и базовые уравнения. В §2 будут представлены численные результаты. В заключительном разделе будут сделаны выводы.

• 1.    Компактные звезды в теории гравитации с неминимальной кинетической связью скалярного поля и кривизны

Теория гравитации с неминимальной кинетической связью скалярного поля и кривизны и космологической постоянной Ло описывается действием вида:

S = / d% ， —g [辰 (R - ^2Л о ) - 2 (^£19 色 + ^f 2 ¹ 2 6Н" ) V"0 ▽ "0] + s (* ,

⑴

где R ii G"" — ска/яр Риччи ii тензор Эйнштейна.呂=8冗G/c4 — постоянная Эйпштсчіііа. с — скорость света, £1,2 = ±1, пара метр I имеет размериость длины, Ло так называемая «голая» космологическая постоянная1. S(m^ — действие для материи, которое описывает идеальную жидкость с тензором энергии-импульса вида

т(^ ) = (рс² + p)u“U" + pg“"

⑵

где U" — 4-вектор скорости, а ， плотность материи р ii давление р свя ： заиы некоторым уравнением состояния. В предыдущей работе [7] в качестве уравнения состояния было рассмотрено простейшее уравнение политропы. В данной работе в качестве уравнений состояния рассмотрены аналитические представления унифицированных уравнений состояния холодного ядерного вещества BSkl9, BSk20, BSk21 (функционалы Брюссель - Монреаль - Скерми) [8]:

с

① ⁺1:1⁺ ； 3 g %⁽a 5 ⁽g - ^аб)) + ^(a 7 +a 89% ⁽ ° 9 ⁽ ° 6 ^- a ) + (。 ¹ 。 + ^aі1 ^ ^{)/О(аі2 ( a} 1 ³ - ^ )) + S1 ⁴ + ^аі5^)^^{о(аі6(аі7 - g))} + 1+ 脸："。 2 。 ) 2 + 1 + £1 - 。 23 ) 2 ,

⑶

где g = lg(p/rcM-3) С = lg(р/дщi см-2). /о(т) = 1/(1 + еж).电-ігзвестиые постоянные. Статическая сферически симметричная метрика имеет вид ds2 = -А(г)с2必2 + j:)+ г2 (d。2 + sin2 9dg2).

⑷

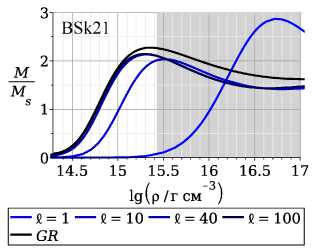
BSk21. При других значениях параметра I и центральной плотности рс графики имеют схожий вид. На границе нейтронной звезды г = R плотность уменьшается до нуля, а графики метрических функций А(г\ 石 (г) сшиваются с внешним вакуумным решением. Сплошная кривая соответствует внутреннему решению, штрихпунктирная кривая соответствует внешнему вакуумному решению (9). Производная скалярного поля 吵 (г) = ф‘ (г) на границе нейтронной звезды обращается в ноль.

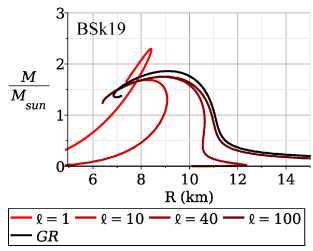
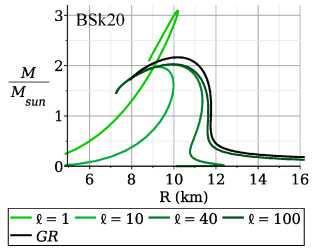
Рис. 2. Диаграммы «масса-радиус» в случае I = 1, 10, 40, 100 км показаны для трех уравнений состояния вещества BSkl9, BSk20 and BSk21 (слева направо). Кривая черного цвета соответствует немодифицирован-ной теории гравитации. По оси ординат отложена асимптотическая масса звезды в единицах масс солнца Msun

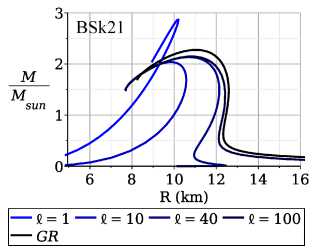
Более детальное представление о параметрах звезд дает диаграмма «масса-радиус». На рис. 2 представлены диаграммы в случае I = 1, 10, 40 и 100 км для трех уравнений состояния вещества BSkl9, BSk20 и BSk21. Кривая черного цвета соответствует немодифицированной теории гравитации. При увеличении параметра I значения масс и радиусов приближаются к данным, полученным при решении классических уравнений Толмена - Оппенгеймера - Волкова (кривая черного цвета). В отличие от немодифицированной теории гравитации, диаграммы смещены в сторону меньших радиусов и меньших масс. В диапазоне 20 Kм < I < 40 км меняется наклон кривых диаграммы: при значениях I < 20 км масса уменьшается с уменьшением радиуса, что характерно для так называемых странных звезд, а при I > 40км, наоборот, растет. Отметим, что при I < 5 KM диаграммы меняют характер поведения, и при уменьшении параметра I смещаются в сторону меньших радиусов, но больших масс. Однако, как это будет показано на рис. 3, такие конфигурации соответ ствуют центральным плотностям в сотни раз превосходящих ядерную плотность, а скорость звука при таких плотностях превышает скорость света для использованных уравнений состояния. Более детально случай малых I будет рассмотрен нами в следующей работе.

Зависимость массы от центральной плотности представлена на рис. 3. Область, отмеченная серым цветом, соответствует значениям центральной плотности рс, при которых скорость звука V2 = с2 (需)I (е - плотность энергии) в центре звезды будет превосходить скорость света, т.е. V2 > с2. В случае I > 10 км максимальные значения масс достигаются при плотностях порядка 1-10 ядерных плотностей. При уменьшении параметра I < 5 км массы порядка 1-3 Msun соответ ствуют центральным плотностям в сотни раз превосходящих ядерную, а скорость звука при таких плотностях превышает скорость света.

Заключение

В данной работе исследованы конфигурации нейтронных звёзд в скалярно-тензорной теории гравитации вида (1), относящейся к классу Хорндески. В данной модели нейтронные звезды рассматривались ранее. Однако в работе [5] был рассмотрен частный случай модели е1 = Л₀ = 0. В работе [7] в качестве уравнения состояния нейтронного вещества было взято лишь простейшее уравнение политропы. В настоящей работе построены конфигурации компактных звезд в теории, описываемой действием (1) при £i,₂ = 0, Л₀ = 0 с реалистичными уравнениями состояния вещества, относящимися к подклассу BSk.

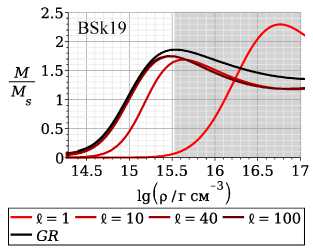
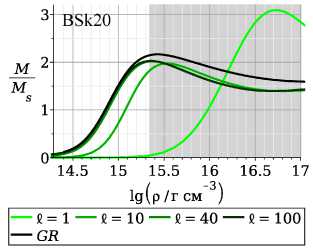
Рис. 3. Зависимость массы звезды от центральной плотности для уравнений состояния BSkl9, BSk20 и BSk21 при различных значениях параметра I = 1, 10, 40 и 100 км. По оси абсцисс отложен десятичный логарифм центральной плотности lg р(0). Сплошная кривая черного цвета соответствует немодифициро-ванной теории гравитации. Область, закрашенная серым цветом, соответствует значениям центральной плотности, при которых скорость звука в среде превосходит скорость света для данного уравнения состояния.

В работе изучены параметры звезд, в том числе получены диаграммы «масса-радиус» для различных значений параметра неминимальной связи I. Было показано, что они кардинальным образом отличаются не только от частного случая а = А = 0 [5] или немодифицированной теории гравитации [8], но и сильно зависят от выбора конкретного уравнения состояния. Уравнения BSk дают большие массы по сравнению с политропным уравнением, рассмотренным в работе [7]. При увеличении параметра I значения масс и радиусов приближаются к данным, полученным при решении классических уравнений Толмена - Оппенгеймера - Волкова. В отличие от немодифицированной теории гравитации, диаграммы смещены в сторону меньших радиусов и меньших масс. В диапазоне 20 Kм < I < 40 км для уравнений класса BSk меняется наклон кривых диаграммы: при значениях I < 20 км масса уменьшается с уменыпением радиуса, а при I > 40 км, наоборот, растет.