Нейтронные звезды в теории гравитации с неминимальной производной связью при наличии заряда скалярного поля. Анализ уравнений состояния и решения скалярного поля

Нейтронные звёзды принадлежат к классу компактных звезд [1]. Их радиус принимает значения в интервале 10 – 13 км, масса в интервале 1.4 – 2 M⊙ масс Солнца, а плотность вещества внутри нейтронной звезды превосходит ядерную в 5-10 раз. Изучение нейтронных звезд позволяет получить информацию о ядерных взаимодействиях при больших плотностях, а также проверить эффекты теории гравитации и протестировать ее различные модификации. Нейтронные звезды рассматривались в различных альтернативных теориях гравитации. В данной работе рассматриваются модели нейтронных звезд в теории гравитации с неминимальной производной связью скалярного поля Ф и тензора Эйнштейна [2-6]

S = У V-g [k(R - 2Л) - 2 (agij - nGij)①旌“ d4x + S(m),               ⑴ где d4x = cdtdV, Л - космологическая постоянная, k = ^g , R — скалярная кривизна, п и a - вещественные параметры модели. Размерность п равна квадрату длины (п > 0), а a - безразмерна. S(m) – действие для материи, которое описывает идеальную жидкость с тензором энергии-импульса ви да

T(m) = (pc2 + p)u“uv + pg“v,                              ⑵ где uµ — 4-вектор скорости, а плотность материи ρ и давление p связаны некоторым уравнением состояния. В качестве уравнения состояния в работе нами используется не только модельное политропное, но также реалистичные уравнения состояния нейтронного вещества.

В данной работе будут рассмотрены сферически симметричные конфигурации с метрикой пространства-времени вида:

ds ²

c     dr²       С / с        с с 、

-A(r)d(ct)2 + в()+ r2 (dӨ2 + sin2 Өdф ), где A(r), B(r) - функции радиальной координаты r. Плотность материи p и давление p являются функциями координаты r и связаны уравнением состояния вещества. Функцию скалярного поля выберем линейно зависящей от времени в виде @(t,r) = F(r) + Qt, где Q - заряд скалярного поля [3-5]. Снаружи нейтронной звезды решение описывается внешним вакуумным решением (р = p = 0). В случае Л = — П (1 — ^Q") вакуумное решение может быть представлено в явном виде [5], 2

в этом случае метрика имеет асимптотику анти - де - Ситтера: A(r) = B(r) = 1 — Г + -^. Далее мы ограничимся этим частным случаем.

Детально параметры нейтронных звезд будут представлены нами в следующей работе. Данная работа посвящена анализу решения для скалярного поля, а также особенностям уравнений состояния, описывающих материю таких звёзд. В §1 будут записаны уравнения для гравитационного и скалярного полей. Будет показано, что вне зависимости от вида уравнения состояния, скалярное поле становится комплексным при Q = 0, что возможно свидетельствует о неустойчивости решения с заряженным скалярным полем. В §2 обсуждаются свойства уравнений состояния, связанные с ограничениями на скорость распространения звука. В последнем разделе будет сде- лано заключение.

• 1.    Базовые уравнения

Независимые уравнения гравитационного поля и закон сохранения тензора энергии-импульса в модели (1) могут быть записаны в виде [4, 5]:

dP dx =2xB 卜x +1 B),                        ⑷ dA dx =xB 卜x2 + 1 - B)，                             ⑸ 砂2 q2 (1 — B + ax2(1 — A)) + 2Px2A =            2AB (1 + ax2)          ，                        (6) dB dx

---y=2, g = 0 ---ү= 2, = 0.192 ---у=2, g = 0.384 ---y=2, g = 0.576  ---y=2, g = 0.768 ---y=2, g = 0.96  ---y= 2, g = 1.152 ——BSkl9,q = 0 ——aSL/9, g = 0.192 ——ВШ9_{> (} ? = 0.384 ——ВШ9, = 0.576 —— BSkl9, q = 0.768 ——BSL/g g = 0.96    BSL/9, g = 1.152

---BS/22, g = 0 —— BSk22,q = 0.192 ——BSk22, = 0.384 —— BSk22, = 0.576 —— BSk22, q = 0.768 ——BS/22, g = 0.96    BS/22, g = 1.152 ---SLy, q = 0 ---SLy, 功, g = 0.384 --- SLy, q = 0.576    — SLy, q = 0.768 --- SLy, SLy, q = 1.152 ---mpal, ^ = 0 --- mpal, q = 0.192 --- mpal, q = 0.384 --- mpal, q= 0.576 --- mpal, q = 0.768 --- mpal, q = 0.96 — mpal, q= 1.152 ---schafl,q=Q——scha 扎 q = 0A92 ——scfey?, g = 0.384——sc%q/7, g = 0.576    sc%q/7, g= 0.768    sc%q/7, g = 0.96    sc%q/7, g = 1.152

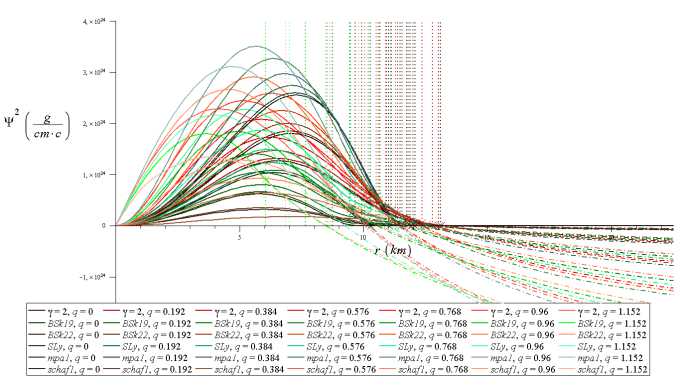
Рис. 1. Кривые разного цвета соответствуют графикам W ² (r) для различных значений параметра q и различных уравнений состояния (BSk19, BSk22, SLy, mpa1, schaf1, уравнению политропы c показателем ү = 2). Сплошная кривая соответствует внутреннему, а штрихпунктирная — внешнему вакуумному решению. Вертикальная прямая соответствует радиусу r = R нейтронной звезды.

— ( ax ² + 1 ) 2 ( ax ² A + 3B )丿 +

+A ( 4 ( 3ax ² ( ax ² + 1 ) — B ( ax ² + 1 ) 2 + a ³ x ⁶ + 1 ) — 4Px ² B ( ax ² + 3 ) —

— 2Ex ² ( B ( ax ² + 1 ) + ax ² ( ax ² + 2

1 δ

q ² I B ( ax ² ( ax ² +5 ) A — ( ax ² — 3 ) B

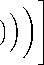
где использованы безразмерные величины

_     2kcP 2kcE 〜kc2q2 丁,   2k r=xw,p=—,p=—, Q2=“，田2=- и 6 = x (1 + ax2) [q2 (ax2A + 3B)— 2A (2 (1 + ax2) + Px2)] , а 3(r) = F‘(r) = Ф‘(г) - производная скалярного поля по r. Чтобы избежать сингулярности решения, знаменатель в уравнении для скалярного поля ⑹ должен быть отличен от нуля, т.е. 1 + ax2 = 0, следовательно параметр a должен быть положительным.

Используя систему уравнений, получим разложение P(x) по степеням x

P(x) = P0 —卓 2(E0 + 3P0—+丁- 3q2) x2 + o(x2),               ⑻ где Po = P(0) и Eo = E(0). В центре звезды x = 0 давление P(x) должно быть максимальным, следовательно коэффициент перед x2 в разложении (8) должен быть меньше нуля. Откуда получаем, что величина q2 может принимать значения в двух диапазонах:

• ¹)    q ² < 3,

  
  

• 2)    q 2 > ⁴ + 込产 2 3       3a

Первое условие не зависит от уравнения состояния. Второе условие можно рассматривать как ограничение на максимально возможное давление в центре.

На границе нейтронной звезды r = R давление обращается в ноль, и внутреннее решение сшивается c внешним вакуумным решением, исследованным в работе [5]. В случае вакуумного решения A(x) = B(x). С учетом P(x) = 0 и A(x) = B(x), уравнение (6) для внешнего вакуумного решения дает выражение для квадрата скалярного поля при r > R

• 2        q ² ( A — 1 )

碑 ac = — 〈_{2 A} 2 丿 .                                       (10)

Поскольку метрическая функция A >  1, то правая часть в (10) становится отрицательной при любых q = 0, а скалярное поле для вакуумного решения — комплексным. Положительность 吵 ² нарушается не только для внешнего вакуумного, но может нарушаться и для внутреннего решения, что подтверждается численным результатом представленным на Рис. (1). В случае q = 0 вакуумное решение ψ _v ² _ac обращается в нуль, и функция скалярного поля будет действительной.

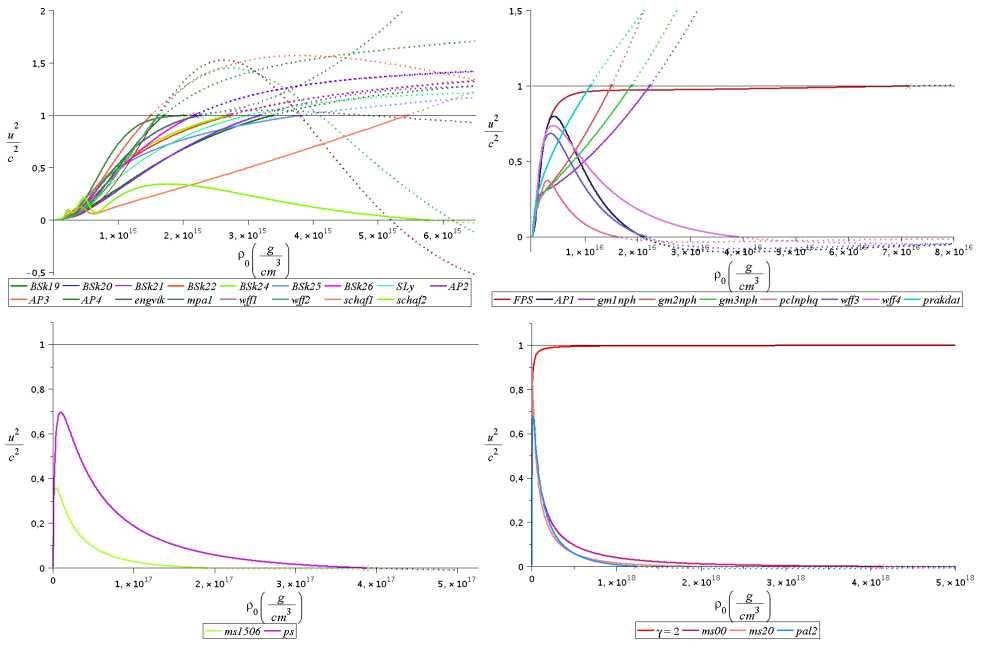
Рис. 2. Графики квадрата скорости звука (в единицах квадрата скорости света) в зависимости от плотности вещества для различных уравнений состояния (политропного уравнения с ү = 2, а также реалистичных уравнений состояния нейтронного вещества). Сплошные кривые соответствуют u ² < c ² , кресты —u ² = c ² , пунктирные кривые — u ² > c ² , либо u ² < 0.

Таким образом это еще раз подтверждает, что рассматриваемые функционалы относят к реалистичному классу уравнений состояния, а сверхплотное состояние материи в нейтронных звездах не позволяет нам неограниченно увеличивать плотность в звезде. Наконец, для политропы таких ситуаций вовсе не наблюдается во всём диапазоне плотностей вплоть до 5 · 10 ¹⁸ _cm ^g ₃ .

Заключение

В данной работе были рассмотрены модели нейтронных звезд в теории гравитации с неминимальной производной связью скалярного поля и тензора Эйнштейна при наличии заряда Q скалярного поля. В качестве уравнения состояния используется не только модельное политропное, но также реалистичные уравнения состояния нейтронного вещества. Было показано, что вне зависимости от вида уравнения состояния, скалярное поле становится комплексным при Q ̸ = 0. Возможно это свидетельствует о неустойчивости решения с заряженным скалярным полем. Также были рассмотрены свойства уравнений состояния, связанные с ограничениями на скорость распространения звука.