Неклассические уравнения математической физики. Фазовые пространства полулинейных уравнений соболевского типа

К настоящему времени обширный класс процессов и явлений в естествознании и технике моделируется уравнениями или системами уравнений в частных производных, не разрешенных относительно старшей производной по времени [46]. Данные конкретные уравнения и системы уравнений редуцируются к абстрактным линейным

Lui = Mu + f                                   (1)

или полулинейным

Lui = Mu + N ( u )                                   (2)

вырожденным операторным уравнениям в банаховых пространствах [47]. Здесь операторы L и M – линейные, подлежащие дальнейшему определению; N – нелинейный, как правило, гладкий оператор. Однако мы для идентификации уравнений вида (1) и (2) будем использовать термин «уравнения соболевского типа» [6, 8, 19, 20, 52, 53]. Этот термин ввел в обиход Р. Шоуолтер [51], чтобы увековечить память о великом российском математике С.Л. Соболеве, который в середине прошлого века инициировал активное изучение таких уравнений (см. прекрасное историческое обозрение в [46]).

Как давно и хорошо известно (см., например, [22–24] и библиографию там же), задача Коши u (0) = u о                                              (3)

в случае ker L * {0}                                          (4)

для уравнений вида (1), (2) разрешима далеко не при всех начальных значениях u 0 . Одним из возможных путей преодоления этой трудности является введение в рассмотрение концепции фазового пространства уравнения (1) или (2). Основы данной концепции заложены в [22] и [23], затем концепция была развита в [24, 25, 3, 27 – 29, 41, 32–34, 37, 4] и многих других работах.

Вкратце суть концепции заключается в следующем. Сначала фазовое пространство определяется как замыкание множества всех допустимых начальных значений u 0 , под которыми понимаются такие векторы, для которых существует единственное (локальное) решение задачи (1), (3) или (2), (3). Затем выбирается такой вектор u 0 , в окрестности O_{u 0} которого фазовое

Математика

пространство Β является гладким банаховым многообразием, причем в этой окрестности O_{u 0} сингулярное (т.е. с условием (4)) уравнение (1) или (2) редуцируется к регулярному уравнению

U = F ( u ), (5)

где F – гладкое сечение касательного расслоения TO_{u 0 .} Завершает рассмотрение ссылка на теорему Коши [16], гарантирующую однозначную локальную разрешимость задачи (3), (5) и, тем самым, задачи (1), (3) или (2), (3).

Другим подходом, позволяющим преодолевать трудности, связанные с несуществованием решения задач (1), (3) и (2), (3), является рассмотрение в случае (4) вместо начального условия Коши (3) начального условия Шоуолтера–Сидорова

P ( u (0) - u ₀) = 0. (6)

Здесь P – проектор, который строится по операторам L , M , такой, что ker P ⊃ ker L . Детальное обсуждение условия (6) можно найти в обзорной статье [38]. Здесь же мы отметим основные особенности условия (6). Во-первых, условия (3) и (6) совпадают, если существует непрерывный оператор L ^{- 1}. Во-вторых, решение задач (1), (6) и (2), (6) существует для всех u 0 (по крайней мере, во всех расмотренных ниже случаях). В-третьих, условие (6) не гарантирует единственности решения задачи (2), (6) в случае (4). Например, в случаях, когда фазовое пространство уравнения (2) лежит на гладком банаховом многообразии, имеющем особенности, такие, как k- сборки Уитни [3, 4, 35, 36].

Однако главное достоинство условия (6) для уравнения (2) в случае (4) раскрывается при постановке вычислительных экспериментов над галеркинскими приближениями точных решений задачи (2), (6) в конкретных ситуациях [2, 11]. Особенно важную роль условие (6) играет при численном исследовании динамической балансовой модели Леонтьева «затраты-выпуск» с учетом капитальных вложений. Эта модель представлена уравнением (1), где L и M – квадратные матрицы одного порядка, причем det L = 0 [12]. Заметим, что в данном случае вырожденная линейная система обыкновенных дифференциальных уравнений с постоянными коэффициентами называется «системой уравнений леонтьевского типа» [39]. Результаты качественного и численного исследования систем уравнений леонтьевского типа выходят за рамки нашего обзора, отметим только их приложения к теории оптимальных измерений [44].

Итак, данная статья имеет обзорный характер и содержит полученные ранее результаты, объясняющие феномены несуществования решений задачи (1), (3) и (2), (3) и неединственность решения задачи (2), (6). В данный обзор не вошли, во-первых, результаты о распространении концепции фазового пространства на полулинейные уравнения соболевского типа высокого порядка [10]. Во-вторых, сюда не вошел обзор результатов о различных обобщениях условия Шоуолтера–Сидорова [7, 9, 31, 54], а также результаты о задаче Шоуолтера–Сидорова для стохастических уравнений соболевского типа [40, 48]. Все эти ранее разрозненные результаты оформились в новые научные направления теории уравнений соболевского типа и ее приложений, которые требуют отдельных подробных обзоров. Наконец, в обзор не вошли результаты (например, [21, 45, 50]), развивающие и обобщающие теорию уравнений, но их авторы не используют ни концепцию фазового пространства, ни неклассические начальные условия вида (6).

Статья содержит обзор работ по изучению морфологии фазовых пространств уравнений соболевского типа и состоит из 4 параграфов, введения и списка литературы. В первом параграфе исследуется существование квазистационарных траекторий задачи (2), (3) в случае ( L , p )-ограниченного оператора M ; приводятся условия простоты фазового пространства обобщенного уравнения Осколкова [34], уравнения плоскопараллельной динамики вязкоупругой несжимаемой жидкости [29]. Во втором параграфе находятся условия существования квазистационарных полутраекторий уравнения (2) в случае ( L , p )-секториального оператора M ; приведены достаточные условия простоты фазового пространства системы уравнений Навье–Стокса [30], уравнения плоскопараллельной конвекции вязкоупругой несжимаемой жидкости [19]. В третьем параграфе приведены условия существования решения задачи (2), (3) в случае s -монотонного, сильно коэрцитивного оператора M и фредгольмова оператора L и получены достаточные условия простоты фазового пространтства обобщенного фильтрационного уравнения Буссинеска

Манакова Н.А.,                            Неклассические уравнения математической физики.

Свиридюк Г.А.             Фазовые пространства полулинейных уравнений соболевского типа и уравнения нелинейной диффузии [28]. В четвертом параграфе изучен феномен неединственности решения задачи Шоуолтера-Сидорова для уравнения Корпусова-Плетнера-Свешникова [35] и приведены условия существования сборок Уитни фазового пространства рассматриваемых уравнений.

1.    Уравнения с относительно p-ограниченным оператором

Пусть U и F - банаховы пространства, операторы L е L(U; F), M е Cl(U; F), оператор N е Ck (U; F),        к е N и {^}.       Рассмотрим      L-резольвентное       множество pL (M) = {ре C: (pL - M)-1 е L(F, U)} и L-спектр 7L (M) = C \ pL (M) оператора M.

Определение 1.1. Оператор M называется ( L, 7 )-ограниченным, если

Я а е R + У р е C (| р |> a ) ^ ( р е p ^L ( M )).

Пусть p ^L ( M ) *0 , через R p ( M) = ( p L - M ) ^{- 1} L и L p ( M ) = L( p L - M ) ^{- 1} обозначим соответственно правую и левую L -резольвенты оператора M .

Лемма 1.1. [52] Пусть оператор M ( L , 7 ) -ограничен, а контур Г = { р е C: | р |= r >  а }. Тогда операторы

P = ^JRp(M)dpе L(U), Q = -LJLp(M)dpе L(F) 2ni Г                    2П Г являются проекторами.

Положим U ⁰ = ker P , U ¹ = im P , F ⁰ = ker Q , F ¹ = im Q. Обозначим через L_k и M_k сужение оператора L и M на U и dom M П U , к = 0, 1, соответственно.

Теорема 1.1. [52] (Теорема о расщеплении) Пусть оператор M ( L, 7 ) -ограничен. Тогда

• (i)    операторы L_k : U^k ^ F^k , M_k : dom n U^k ^ F^k , к = 0, 1;

• (ii)    существуют операторы M ₀ ¹ е L( F ⁰, U ⁰);

• (iii)    операторы H = M ₀ ¹ L ₀ е L( U ⁰), S = L - ¹ M 1 е L( U 1 ).

Определение 1.2. Оператор M называется ( L , p )-ограниченым, если он ( L, 7 )-ограничен и Я p е {0} и N: H^p * O, а H^{p + 1} = O.

Определение 1.3. Вектор-функцию u е C (( - т , т ); U ), к е N и { ^ }, назовем решением уравнения (2), если она при некотором те R ₊ удовлетворяет ему. Решение u = u ( t ) уравнения (2) назовем решением задачи Коши (2), (3), если оно еще и удовлетворяет начальному условию (3).

В дальнейшем будем рассматривать ( L , p )-ограниченный оператор M . В силу теоремы 1.1 уравнение (2) редуцируется к паре эквивалентных ему уравнений

Hut ⁰ = и ⁰ + M 0 ^{- 1} ( I - Q ) N ( и ),                                  (7)

i/ 1 = Su ¹ + L - 1 QN ( и ),                                         (8)

где u ¹ = Pu , u ⁰ = u - u ¹.

Определение 1.4. Вектор-функция u = u ( t ) называется квазистационарной траекторией уравнения (2), если H it( t ) = 0 при всех те R ₊ . Если квазистационарная траектория уравнения (2) удовлетворяет условию Коши (3), то она называется квазистационарной траекторией уравнения (2), проходящей через точку u ₀.

Замечание 1.1. Любая стационарная траектория уравнения (2) будет квазистационарной, однако обратное неверно. В случае ( L , 0)-ограниченности оператора M все решения уравнения (2) являются квазистационарными траекториями.

В дальнейшем мы ограничимся рассмотрением только квазистационарных траекторий. Введем в рассмотрение множество

В = { u е U :(I - Q )( Mu + N ( u )) = 0}.

Из (7) и теоремы о расщеплении вытекает, что, если u = u ( t ) - квазистационарная траектория уравнения (2), то она с необходимостью лежит во множестве В , т.е. u ( t ) е В при всех t е ( - т , т ).

Математика

Возьмем точку и ₀ еВ и обозначим через F'0 сужение оператора (I - Q )( М + N_{U o})(I - Р ) на подпространство U , здесь N ‘ 0 - производная Фреше оператора N в точке и ₀. В силу построения оператор F^ е L(U ⁰; F ⁰). В дальнейшем нам понадобятся следующие условия:

В * 0 ;                                         (9)

оператор F„0 - диффеоморфизм.                         (10)

Теорема 1.2. [34] Пусть оператор М ( L , p )-ограничен, p е {0} u N, причем выполнены условия (9), (10). Тогда существует единственная квазистационарная траектория уравнения (2), проходящая через точку и ₀.

Определение 1.5. Множество Ес U называется фазовым пространством уравнения (2), если

• (i)    любое решение и = и ( t ) лежит в Е как траектория, т.е. и ( t ) е Е при любом t е ( - т , т );

• (ii)    при любом и о еЕ существует единственное решение задачи (2), (3).

Определение 1.6. Пусть точка и о еВ , положим и 0 = Ри ₀ е U ¹. Множество В в точке и ₀ является банаховым C k -многообразием , если существуют окрестности О 0 с В и О 0 с U ¹ точек и ₀ и и 0 соответственно и С -диффеоморфизм 5 : О 0 ^ О ^ такой, что 5' равен сужению проектора Р на О ^ . Множество В называется банаховым С^к -многообразием, моделируемым пространством U ¹ , если оно является банаховым С^к -многообразием в каждой своей точке. Связное банахово С^к -многообразие называется простым , если любой его атлас эквивалентен атласу, содержащему единственную карту.

Следствие 1.1. [34] Пусть оператор М ( L , p )-ограничен, p е {0} u N, причем выполнены условия (9), (10). Тогда фазовым пространством уравнения (2) служит простое многообразие , моделируемое подпространством U ¹ .

1.1.    Обобщенное фильтрационное уравнение Осколкова

В цилиндре Qx R рассмотрим задачу Коши-Дирихле и (x ,0) = и 0( x), x еQ,    и (x, t ) = 0, (x, t) едQx R +                  (11)

для обобщенного уравнения Осколкова

( A -А ) и = а А и - K ( и ) + f , K (0) = 0,< K ( и ), и > >  0,                  (12)

описывающего динамику давления неньютоновой жидкости, фильтрующейся в пористой среде. Уравнение (12) моделирует широкий класс процессов фильтрации вязкоупругих жидкостей [17].

О

Для того чтобы редуцировать задачу (11), (12) к задаче (2), (3) положим U = W ₂ 1 ( Q ) n W ₂ m ^{+ 2}( Q ), F = W m ( Q ), m е {0} и N, зададим операторы L = A -А , М = а А . По построению операторы L , М е L( U ; F ), причем оператор L фредгольмов.

Лемма 1.2. [34]

• (i)    При всех а е R ₊ оператор М ( L , 0)-ограничен.

• (ii)    При любом векторе f е F , m + 2 >  n /2 и любой функции K е С ” ( Q ) оператор N : и ^ K ( и ) - f принадлежит классу С ” ( U ).

Обозначим через { ф 1 } собственные функции однородной задачи Дирихле для оператора А , а через { A l } - соответствующие им собственные значения, занумерованные по неубыванию. Зафиксируем f е F и построим множество

В f = { и е U :< Ми - N ( и ) - f , ф ₁ >= 0, A = A l } .

Замечание 1.2. Поскольку оператор М ( L , 0)-ограничен, то все решения уравнения (12) являются квазистационарными траекториями.

Теорема 1.3. [34] Пусть ае R + , m >  n /2 - 2, f е F . Тогда

• (i)    если ker L = {0}, то фазовым пространством уравнения (12) служит все пространство U ;

• (ii)    если ker L Ф {0}, то фазовым пространством уравнения (12) служит простое многообразие В f , моделируемое подпространством U ¹ = { и е U : ^ и,ф^ = 0, 2 = X } .

1.2.    Плоскопараллельная динамика вязкоупругой несжимаемой жидкости

Пусть Qc R2 - ограниченная область с границей dQ класса C”. В цилиндре Qx R рассмотрим задачу Коши-Дирихле и (X, У ,0) = и о( x, y), (x, y) eQ;(13)

и (x, y, t ) = А и (x, y, t ) = 0, (x, y, t) eдQx R(14)

для уравнения ди     , 2    д( и, А и)    „....

(1 — ХА)А— = vA2и - у /+ f.(15)

д t            д ( x , y )

Положим

U = { и е ^ ₂⁴( Q ): и ( x ) = А и ( x ) = 0, x е dQ }, F = L ²( Q ).

Зададим операторы

• L : и ^ (1 - х А ) А и , М : и ^ | А ² и , N : и ^- ^{д( и} ,^{А и} ) + f .

д ( x , y )

Лемма 1.3. [29]

• (i)    При любых v , хе R \ {0} операторы L , М е L( U ; F ) фредгольмовы.

• (ii)    При любых значениях параметров v , хе R \ {0} оператор М ( L, о ) -ограничен.

• (iii)    Оператор N е C ” ( U ; F ).

Обозначим через <г ( А ) спектр однородной задачи Дирихле в области Q для оператора Лапласа А , а через { 2 к } множество собственных значений, занумерованное по невозрастанию с учетом кратности, { ф к } - семейство соответствующих собственных функций, ортонормированных относительно скалярного произведения <  • , • > из L ²( Q ). Пусть х ¹ е О "( А ), тогда в силу фредгольмовости оператора L ker L = span{ ^ ₁, ^ ₂,---, W _m }, где W i е { ф _к }, l =1,2,..., m . Построим множество

В = {и е U :< Ми + N ( и )^"; >=0, l = 1,2,..., m }.

Положим U ⁰=ker L , U 1=ker L ¹ , где ортогональность понимается в смысле L ₂( Q ). В силу фредгольмовости оператора L имеет место расщепление U = U ⁰ © U ¹.

Теорема 1.4. [29]

• (i)    Пусть х^-1е R\ у(А) , тогда фазовым пространством уравнения (15) является все пространство U.

• (ii)    Пусть х^-1е^(А), ve R\{0}. Тогда множество В - простое C” -многообразие, моделируемое подпространством U¹ .

2. Уравнения с относительно p-секториальным оператором

Пусть U и F - банаховы пространства, операторы L е L( U ; F ), М е Cl(U; F ).

Определение 2.1. Оператор М называется ( L , p )-секториальным с числом p е {0} и N, если

π

• (i)    существуют константы a е R и 0е ("^ Л ) такие, что сектор

S” L ^ ( М ) = { ^ е C: | arg( ^ - a )|< 0 , ц Ф a } c p^L ( М );

• (ii)    существует константа K е R ₊ такая, что

• Математика

max { || R ^p ) ( M )W_L(UVU^p ) ( M ) |^ } < --------

Пк -al q=0

при любых ко, Ц1,^, up e S^q (M). Здесь pp

R L p ) ( M ) = № q L - M ) ^{- 1} L, L p ) ( M ) = П L( ^ q L - M ) - 1 .

q=0

Пусть выполнено условие

U = U0 © U 1, F = F0 © F 1.(16)

Тогда, аналогично п. 1, действия операторов L и M расщепляются, а через L k и M_к обозначим сужение операторов L и M на U k и dom M n U^k , к = 0, 1, соответственно. Пусть выполнено условие

Я L-1 e L(F 1; U 1).(17)

Тогда оператор H = M ₀ 1 L ₀ e L( U ⁰) нильпотентен степени не выше p e {0} и N и оператор S = L - ¹ M 1 e L( U 1 ) секториален.

Замечание 2.1. Пусть оператор M ( L , p )-секториален, p e {0} и N и выполнены условия (16), (17), тогда оператор M сильно ( L , p )-секториален [26, 30].

Рассмотрим секториальный оператор A e Cl(U ) такой, что Re G (A )<0. Для любого a >0

положим

∞

A ^-a = — № ^{- 1} e ^{- At}dt . Г ( а ) J

Определим A ^a как оператор, обратный к A ^-a , dom A ^a = im A ^-a , A ⁰ =I. Далее положим для каждого a > 0, U ^a = dom A ^a и наделим пространство U ^a нормой графика || u|| _a =| A ^a u ||, u e U ^a . Выберем константу c e R + таким образом, чтобы Re ^ ( S - cl ) <  0. По оператору A = S - c I построим пространства U ^a , a >  0. Нормы || • || _a при фиксированном a и различных c эквивалентны.

Теорема 2.1. [25] Пусть оператор M ( L , p )-секториален, p e {0} и N и выполнены условия (16), (17). Тогда U ^a - банахово пространство с нормой |р || _a для a >0, причем U ⁰ =U и U ¹ = dom A . Для a >  в >  0 пространство U ^a плотно в U ^в и вложение U^a с U^в непрерывно.

Пусть U 1 линеал dom M n U 1 , снабженный нормой графика, и U 1 ⁰ = dom M n U ⁰, положим U _a = U 0 © U ^a . Пусть при некотором фиксированном a e [0,1) оператор N e C ” ( U _a ; F ), тогда рассмотрим задачу Коши (3) для полулинейного уравнения соболевского типа (2).

Определение 2.2. Вектор-функцию ue C 1((0,T);U) nC((0,T);Ua) назовем решением уравнения (2), если она при некотором Te R + удовлетворяет ему. Решение u = u(t) уравнения (2) назовем решением задачи Коши (2), (3), если оно еще и удовлетворяет lim || u(t) -u0 ||U = 0 при t ^0+             a некотором u0 e Ua .

Пусть оператор M ( L , p )-секториален, p e {0} и N, и выполнены условия (16), (17), тогда в силу теоремы о расщеплении [26] уравнение (2) редуцируется к паре эквивалентных ему уравнений (7), (8).

Определение 2.3. Вектор-функция u = u(t), te (0,T), называется квазистационарной полутраекторией уравнения (2), если Hu (t) = 0 при всех Te R +. Если квазистационарная полутраектория уравнения (2) удовлетворяет условию lim || u(t)-u0 ||U =0, то она называется t→0+            α квазистационарной полутраекторией уравнения (2), проходящей через точку u0.

Замечание 2.2. Понятие квазистационарной полутраектории вводится по аналогии с понятием квазистационарной траектории (см. п. 1). В случае ( L , 0)-секториального оператора M любое решение уравнения (2) является квазистационарной полутраекторией.

В дальнейшем мы ограничимся рассмотрением только квазистационарных полутраекторий. Аналогично п. 1, квазистационарные полутраектории поточечно принадлежат множеству

Β ={ u ∈ U :(I - Q )( Mu + N ( u ))=0}.

Предположим, что множество

Β≠ ∅ .                                   (18)

Теорема 2.2. [25] Пусть оператор M ( L , p )-секториален, причем выполнены условия (16), (17), а оператор N ∈ C ^∞ ( U_α;F ). Пусть в точке u ₀ ∈ Β множество Β является банаховым C ^∞ -многообразием. Тогда существует единственная квазистационарная полутраектория уравнения (2), выходящая из точки u 0 .

Определение 2.4. Множество Ξ ⊂ U _α называется фазовым пространством уравнения (2), если

• (i)    любое решение u = u(t) уравнения (2) лежит во множестве Ξ поточечно, т.е. u(t) ∈Ξ , t∈(0, τ) ;

• (ii)    при любом u₀∈Ξ существует единственное решение задачи (2), (3).

2.1.    Система уравнений Навье–Стокса

Замечание 2.3. Если выполнены условия теоремы 2.2, то некоторая окрестность O ₀ ⊂ Β точки u ₀ ∈ Β лежит в фазовом пространстве уравнения (2). Если множество Β является простым банаховым C ^∞ -многообразием, то оно совпадает с фазовым пространством уравнения (2).

В цилиндре Ω× R рассмотрим задачу Коши–Дирихле (11) для системы уравнений Навье – Стокса [25, 30]

( λ - ∇ ²) u_t = ν ∇ u - ( u ⋅∇ ) u - ∇ p + f , ∇ ( ∇⋅ u )=0,                   (19)

которая моделирует динамику вязкой несжимаемой жидкости; здесь ∇ p – градиент давления, вектор-функция u = u ( x , t ) = ( u ₁, u ₂,..., u_n ) – вектор скорости жидкости, f = f ( x , t ) = ( f ₁, f ₂,..., f_n ) – вектор объемных внешних сил, ν ∈ R ₊ – кинематический коэффициент вязкости.

Положим Hσ2 и Hπ2 (Hσ и Hπ ) – подпространства соленоидальных и потенциальных вектор- функций [15, 43] пространства H2=(W22(Q) n W"2(Q)) n (L2=(L2(Q)) n). Оператор A = diag{V2,..., V2} является линейным непрерывным оператором с дискретным конечнократным отрицательным спектром σ(A), сгущающимся лишь на -∞ . Обозначим через

A _{σ ( π )} сужение оператора A на H _σ ² _{( π )}. Зададим оператор K : u → ∇ ( ∇⋅ u ), оператор K ∈ L( H ², H _π )

и ker K = H _σ ² . Обозначим через Π ∈ L( H ², H _π ²) проектор вдоль H _σ ² и построим проектор Σ =I -Π .

Положим U = H _σ ² × H _π ² × H _p , F = H _σ × H _π × H _p , где H _π = H _σ . Формулами

L =

' Е	O	0 ^		' r A ff	O	O
O	Π	O	, M =	ν A π	ν A π	-Π
. 0	O	0 >		1 0	K	O

/

л зададим операторы L∈ L(U; F) , imL = Hσ×Hπ×{0} , kerL = {0} ×{0} ×Hp и M ∈ Cl(U;F),

О

W ¹₂( Ω )

n

dom M = H ² × H ² × H ². Положим H ¹= σπ p

Математика

Лемма 2.1. [25]

• (i)    При любых ve R + оператор M ( L , 1)-секториален и выполнены условия (16), (17).

• (ii)    При n e {2,3,4} оператор C : v ^ ( v -V ) v принадлежит классу C ” ( H 1 ( Q ); L ²( Q )). Построим оператор

• 2.2.    Плоскопараллельная конвекция вязкоупругой несжимаемой жидкости

N ( и ) = col( S C ( и ), П C ( и ), 0), и = u ^ + и _п .

Оператор Ne C”(HL хHl хH-И.- хH_ хH„) и domM с H1 хHl хH„ с U, где линеал domM σπ pσπ p       σπ p снабжен «нормой графика». Подпространство U 1 = H^ х {0} х {0}, тогда domM n U 1 = H2 х {0} х {0}. Отсюда H^ х {0}х {0} = U1 ]1/2, где U1=domM n U 1. Далее построим U0 = domM n U0 = {0} х Hn х Hp . Поэтому Ua = H^ х Hn х Hp . Получим, что оператор N e C” (Ua ;F). Множество, содержащее квазистационарные траектории, имеет вид

^В = { ^{и e} U a ^{: и} п =^{0, и} р = ^-П C ^{( и} а ) } •

Теорема 2.3. [30] При любых n e {2,3,4}, v e R ₊ фазовым пространством уравнений (19) служит простое банахово многообразие В , моделируемое подпространством H 1 х {0} х {0}.

Пусть Q = (0, l ) х (0, h ) с R² . В области Qх R ₊ рассмотрим задачу Бенара

у(x,0, t) = Ay(x,0, t) = 0, у(x, h, t) = Ay(x, h, t) = 0,(20)

0( x ,0, t ) = 0( x, h, t ) = 0,(21)

функции 0 и у периодичны по x с периодом l,(22)

У ^{( x} , У ,⁰⁾ = У 0 ^{( x} , У ),    ^{0 ( x} , У ^,0) = ⁰ 0 ^{( x} , У )

для системы уравнений

• л ду   . 2 д(у, Ау)

• (1 — ХА)А^ = vA2y —+ g^, д t д( x, у)

• *=йда-.^)+в у, дx          д( x, у)

которая моделирует термоконвекцию вязкоупругой несжимаемой жидкости Кельвина-Фойгта [14]. Здесь функция 0 = 0 ( x , t ) соответствует температуре жидкости, параметр Se R ₊ характеризует температуропроводность, g - ускорение свободного падения. Положим

U = Uy х U0, F = Fy х F0, где

U _y ={ y e W^( ^ ) : у удовлетворяет (20), (22)}, U ₀ = { у e W ₂⁴ ( Q ): 0 удовлетворяет (21), (22)}, F y = F 0 = L ²( Q ).

Зададим операторы

( (1 - x A ) A O A

I ^O       I J ’

M =

' _ga д0 д ( у , A y ) д x    д ( x , у )

в ду д ( у , 0 )

_v д x д ( x , у ) _v

v A ²

I ^O

и =

O ) S A J ’ ( у , 0 ).

Тогда domM = Uy x (0e W22(Q): 0 удовлетворяет (21), (22)}.

Лемма 2.2. [14]

• (i)    При любых xg R \ {0} оператор L g L( U ; F ) фредгольмов.

• (ii)    При любых значениях параметров v,5g R + , x g R \ {0} оператор M сильно ( L , 0)-секториален.

• (iii)    Оператор N g C ” ( U ; F ).

Рассмотрим пространство

UN = Uy x {0 g W2(Q): 0 удовлетворяет (21), (22)} и множество д0 d(y,Ay)

^В N = ^{( У , ^{0 ) g} U N ^:< ^V X У ⁺ 8«к ---г², ^ / >=^0, l = ^1,2, ^ ^,dimker( X ^{-A )}}.

d x    d ( x , y )

Теорема 2.4. [14] Пусть v , ^ g R ₊ и, если

• (i)    X^-1g \^(A), тогда фазовым пространством системы уравнений (24) служит множество UN^;

• (ii)    X^-1g у(А) , тогда фазовым пространством для системы уравнений (24) служит простое банахово C” -многообразие В _N, моделируемое подпространством

3. Уравнения с s-монотонным и сильно коэрцитивным оператором

U N = {( у , 0 ) g Un : <  У , ^ >= 0, l = 1,2, _ ,dimker( x ^{- 1} - A )}.

Пусть H = ( H ; (•, •)) - вещественное сепарабельное гильбертово пространство, отождествленное со своим сопряженным; ( A , A * ) и (V , V * ) - дуальные (относительно двойственности (•, •)) пары рефлексивных банаховых пространств, причем вложения

V с A с H с A * с V *                                (25)

плотны и непрерывны. Пусть L g L ( A ; A * ) - линейный, непрерывный, самосопряженный, неотрицательно определенный, фредгольмов оператор, N g C r (V ; V * ), r >  1 - s -монотонный (т.е.

< N ( u + v ), v >_.                   _

(N_uv , v) >0, u , v Ф 0) и сильно коэрцитивный (т.е. l_im--- +^ V u g V ) оператор.

'       '                                                      II v l V ^     II ^v I V

Рассмотрим задачу Коши (3) для полулинейного уравнения соболевского типа

.

Lu + N ( u ) = f . (26) Ввиду самосопряженности и фредгольмовости оператора L отождествим A з ker L = coker L с A * , тогда A * = coker L © im L . Обозначим через im L замыкание im L в топологии V * , тогда V * = co ker L © im L . Обозначим через Q проектор V * вдоль coker L на im L и сделаем допущение:

(I - Q ) f не зависит от t g (0, 7 ).

Тогда, если u = u ( t ), t g (0, 7 ), - решение уравнения (26), то оно с необходимостью лежит во множестве

_В = Г { u g V :(I - Q ) N ( u ) = (I - Q ) f }, если ker L Ф {0}; f [             V , если ker L = {0}.

Введем в рассмотрение множество coimL = {ug A:Ци,v) = 0 Vvg kerL\{0}}.

^

Обозначим через P проектор вдоль ker L на coim L n V = V . Ввиду (25) V = ker L © V .

^^

Математика

Теорема 3.1. [28] Пусть выполнено условие (27), тогда множество В f есть банахово C -многообразие, диффеоморфно проектирующееся вдоль ker L на V всюду, за исключением, быть может, точки нуль.

3.1.    Обобщенное фильтрационное уравнение Буссинеска

В цилиндре Qx R + рассмотрим задачу Коши-Дирихле (11) для обобщенного фильтрационного уравнения Буссинеска

( 2 -A ) u_t -A (| u | ^{p - 2} u ) = f , p >  2,                             (28)

которое моделирует процесс фильтрации жидкости. Здесь искомая функция u = u ( x,t ) отвечает потенциалу скорости движения свободной поверхности фильтрующейся жидкости; параметры ае R + , 2 е R характеризуют среду, причем параметр 2 может принимать отрицательные значения; свободный член f = f ( x , t ) соответствует внешнему воздействию.

Положим H = W ₂ ^{- 1}( Q ), A = L ₂( Q ), V = L_p ( Q ). В силу теоремы вложения Соболева при

2 П                              Г p >---- пространства W 2(Q) с L (Q) вложены непрерывно, поэтому выполнено непрерывное n + 2                        4

вложение L_p ( Q ) с W₂ ¹ ( Q ). Определим в H скалярное произведение формулой U u , v ^ = J uv dx V u , v е H ,

Ω где v - обобщенное решение однородной задачи Дирихле для оператора Лапласа (-A) в области Q. Положим V*=(Lp(Q))* и A*=(L2(Q))*, где (Lp(Q))* - сопряженное относительно двойственности (29) пространство, и выполнено непрерывное вложение W^1 (Q) с (Lp (Q))*. При таком определении A* и V* имеют место плотные и непрерывные вложения (25). Операторы L и M определим следующим образом:

( Lu , v ) = J ( 2 uv + uv ) dx , u , v е A;

Ω

( N ( u ), v ) = J | u |^{p - 2} uvdx , u , v е V .

Ω

Обозначим через { ф _к } последовательность собственных функций однородной задачи Дирихле для оператора Лапласа ( -A ) в области Q , а через { 2 k } - соответствующую последовательность собственных значений, занумерованную по неубыванию с учетом кратности.

Лемма 3.1. [28]

• (i)    При всех 2 >-2 1 оператор L е L( A ; A * ) самосопряжен, фредгольмов и неотрицательно

определен, причем ортонормальное семейство { ф к } его функций тотально в пространстве A .

• (ii)    Оператор N е C 1 (V ; V * ) s -монотонен и сильно коэрцитивен.

Постороим проектор

Q =

I, если 2 *-2 1 ;

I -(- , ф 1), если 2 = -2 1

и множества

• V , если 2 >  -2 1 ;

  Β

  
  

1 f = “ {uе V: J | u Ip-2 uф1 dx = Jf ф dx}}, Q             Q если 2 = -21,

coim L =

A ,   если 2 >  - 2 1 ;

{ u е A : ( u , ф 1) = 0}, если 2 = -2 1 .

2 n

Теорема 3.2. [28] Пусть p >---- и выполнено условие (27). Тогда множество В f - простое n + 2

банахово C 1 -многообразие, моделируемое пространством coim L n V.

• 3.2.    Уравнение нелинейной диффузии

В цилиндре Qx R ₊ рассмотрим задачу Коши-Дирихле (11) для уравнения

(Л -A) ut - div(| V и |p-2 V и ) = f,       p > 2, которое моделирует процесс нелинейной диффузии [5]. Здесь искомая функция и = и(x,t) отвечает потенциалу концентрации вещества; параметр Ле R - коэффициент вязкости.

01                   01              ,          ,*

Положим H = L 2(Q), A = W 2(Q), V = Wp (Q), A = W21(Q), V = Wp1(Q). Определим в H скалярное произведение формулой

(и , v) = j uvdx V и , v е H .

Ω

При таком опеределении пространств A и V имеют место плотные и непрерывные вложения (25). Операторы L и N определим следующим образом:

( Lu , v ) = j ( Л V и V v + uv ) dx , и , v е A ;

Ω

( N ( и ), v ) = j | V и I^{p - 2} V и V vdx , и , v е V .

Ω

Лемма 3.2. [28]

• (i)    При всех Л > - Л 1 оператор L е L( A ; A * ) самосопряжен, фредгольмов и неотрицательно

определен, причем ортонормальное семейство { ф к } его функций тотально в пространстве A .

• (ii)    Оператор M е C 1 (V ; V * ) s -монотонен и сильно коэрцитивен.

Построим проектор

• f I, если Л * - Л ;

Q = 1

[ I -(- , ф ^, если Л = - Л 1 .

Множества f            V, если Л > -Л1;

В f = 1         , х , >            „        coim L = f   [{и е V: (N(и),Ф1} = {f,Ф1)},   если Л = -Л1,

A , если Л

-

{ и е A : ( и , ф ^ = 0}, если Л = -Л 1 .

Теорема 3.3. [28] Пусть Л >- Л 1 и выполнено условие (27). Тогда множество В f - простое банахово C 1 -многообразие, моделируемое пространством coim L n V .

4.    Особенности фазового пространства

Перейдем к рассмотрению случаев, когда фазовое пространство В не является простым банаховым многообразием, что может повлечь неединственность решения задачи Шоуолтера-Сидорова (2), (6). При помощи исследования морфологии фазового пространства удается изучить данные особенности. Пусть выполнены все условия на пространства и операторы п. 2.

Определение 4.1. Пусть функция G е C ~ ( R x U ;R ) . Уравнение G ( x , v ) = 0 определяет k -сборку Уитни над открытым множеством V с U , если существуют функции g ₀, g 1 ,..., g_k е C ” ( V ;R) такие, что это уравнение эквивалентно уравнению

0 = g ₀( и ) + g 1 ( и ) x + ... + g k ( и ) x^k + x^{k + 1} V и е V .

Определение 4.2. Пусть вектор ф ₀ е ker L \{0}, упорядоченное множество векторов { ф 1 , ф ₂,...} называется цепочкой M -присоединенных векторов собственного вектора ф ₀, если

L ф _{k + 1} = M ф _k. , k = 0,1,..., ф ₁ С ker L \{0}, l = 1,2,...

Математика

Порядковый номер вектора в цепочке будем называть его высотой, а порядковый номер последнего вектора в конечной цепочке - длиной этой цепочки.

Теорема 4.1. [52] Пусть оператор L фредгольмов. Тогда следующие утверждения эквивалентны

• (i)    оператор M (L, p)-ограничен, p е {0} u N;

• (ii)    длина любой цепочки M-присоединенных векторов оператора L ограничена числом p е {0} u N.

4.1.    Уравнение Хоффа

Рассмотрим случай, когда оператор L фредгольмов и не имеет M -присоединенных векторов, но имеет ( M + N U 0 ) -присоединенные векторы и dimker L = 1.

Теорема 4.2. [36] Пусть оператор L фредгольмов и dimker L = 1. Пусть оператор L не имеет M -присоединенных векторов, но имеет в некоторой точке и о е U ( M + N 0 ) -присоединенные векторы высоты не больше p е N. Тогда в некоторой окрестности О_и 0 с U точки и ₀ уравнение (2) может быть приведено к виду

£ q = ^ q - 1 ⁺ g q - 1 ^{( U} ), Q ⁼ 1,2,..., F ,

0 = ^ + g p ( и ),                                    (31)

U 1 = Su ¹ + F ( и ), F = L - ¹ QN е C ” ( U ; U 1 ).

Пусть Qc R n - ограниченная область с границей dQ класса C ” . В цилиндре Qx R рассмотрим обобщенное уравнение Хоффа [49]

( Л + A ) U t = а 1 и + а 2 U + ... + a k U   ,                          (32)

моделирующее выпучивание двутавровой балки, находящейся под постоянной нагрузкой. Здесь искомая функция и = и ( x,t ), ( х , t ) е Qx R имеет физический смысл отклонения балки от вертикали, параметры a _i е R \{0}, i = 1,..., к , характеризуют свойства материала балки, параметр Ле R ₊ характеризует нагрузку на балку. Рассмотрим задачу Коши-Дирихле (11) для уравнения (31). О

Пусть U = W ^ ( Q ), F = W ₂ ^{- 1} ( Q ), зададим операторы

< Lu , v ) = J ( A uv -V и V v ) dx , V и , v е W ^Q ),

Ω

< Mu , v ) = a , J uvdx , V и , v е L _{2 k} ( Q ),

Ω

< N ( и ), v ) = J ( a ₂ и ³ + ... + a _k - 1 и ^{2 k - 3} + a k u ^{2 k - 1}) vdx V и , v е L _{2 k} ( Q ).

Ω

О

В силу теорем вложения Соболева вложение W ₂ 1 ( Q ) с L ₂ к ( Q ) плотно и непрерывно, следовательно, операторы L , M е L(U;F ), причем оператор L фредгольмов.

Лемма 4.1. [32]

• (i)    При всех a , е R\ {0}, тогда оператор M ( L , 0)-ограничен.

• (ii)    Оператор N е C ” (U;F ), если к = 1, 2 при n = 4 или к = 1, 2, 3 при n = 3 или к е N при n = 1, 2.

Обозначим через { ^ l } собственные функции однородной задачи Дирихле для оператора A , а через { Л 1 } - соответствующие им собственные значения, занумерованные по неубыванию. Построим множество

В = { и е U : J _Q ( a 1 + a ₂ и ² + ... + а _ки ^{2 к - 2}) и ф ^х = 0, Л = - A l } .

Замечание 4.1. Поскольку оператор M ( L , 0)-ограничен, то все решения уравнения (32) являются квазистационарными траекториями.

Теорема 4.3. [32] Пусть к = 1, 2 при n = 4 или к = 1, 2, 3 при n = 3 или к е N при n = 1, 2. Тогда

• (i)    если ker L = {0}, то фазовым пространством уравнения (32) служит все пространство U ;

• (ii)    если ker L Ф {0}, все коэффициенты а _i е R\{0}, I = 1, ..., к одного знака, то фазовым пространством уравнения (32) служит простое многообразие В , моделируемое подпространством U ¹ = { и е U : ( и ,у) = 0, Л = - Л _; }.

Рассмотрим задачу Коши-Дирихле для уравнения Хоффа (11), (32) в случае к = 2 и dimker L = 1. Построим проектор I - Q =< •у >, где у е ker L , | | у || L ( Q )=1, и множество

Е = { и е U : <  Mu + N ( и ), у >= 0}.

Построим подпространство U ¹ = { и е U :< и, у >=0} и представим вектор и = s y + v , тогда множество Е C ” -диффеоморфно множеству

s

( s , v ) е R х U : s ³ || у || U + 3 s ² j у ³ vdx + s

Ω

j у ² v ² dx + а 1 а ₂ ¹ У Q

+ j y v ³ dx = 0 > .

Q              .

Выделим во множестве Е подмножество

E ' = { u е U :< M y + N ^ V^ >=0} nE .

Множество E ' C ” -диффеоморфно множеству

s

( s , v ) е R x U ¹:3 s ² || у || U + 6 s | у³ vdx + 3 j у ² v ² dx + а ₁ а₂^х =0 >n

.

Ω

Ω

Теорема 4.4. [36] Пусть 1 <  n <  4, а 1 а ₂ <0, Л = Л 1 . Тогда

• (i)    любой вектор ^е ker L \ {0} не имеет ( M + N'_u )-присоединенных векторов, если

u ∈

;

• (ii)    любой вектор ^е ker L \ {0} имеет точно один (M + N)-присоединенный вектор, если и е Е '\U¹.

4.2.    Уравнение Корпусова–Плетнера–Свешникова

Замечание 4.2. Множество Е _s образует 2-сборку Уитни.

Пусть Q = ( a , b ) c R. В цилиндре Qx R ₊ рассмотрим уравнение Корпусова-Плетнера-Свешникова

( Л - A ) u t = а А и - в div( u grad и ),

моделирующее метастабильные процессы в жидком двухкомпонентном полупроводнике. Параметры а , в , Л е R характеризуют свойства полупроводника. В случае отрицательности коэффициента Л возможен пробой полупроводника. Впервые уравнение (33) было получено в работе [13] и была установлена однозначная разрешимость начально-краевой задачи для уравнения (33) в случае положительности параметра Л .

О

Положим U = W 2 ( Q ), F = W ₂ ^{- 1}( Q ). Пространство F сопряжено к U относительно скалярного произведения <  • , • > из L ₂ ( Q ). Операторы L , M и N определим следующим образом: bb

< Lu , v >= j ( Л uv + u_xv_x ) dx , <  Mu , v >= - j a u x v x dx , и , v е U , aa

b

N ( и ), v >= - j e uu x v x dx , и , v е U .

a

Математика

По построению операторы L , M е L(U;F ) и фредгольмовы. Обозначим через { X k } занумерованное по невозрастанию множество собственных значений однородной задачи Дирихле для оператора Лапласа А на ( a, b ), а через { ф _к } - ортонормированное в смысле L ₂ ( Q ) множество соответствующих собственных функций. Построим множество

Е = {ие U: ^(Mu + N(и)),ф^ = 0, X = Xl} и пространства

U ⁰ = ker L = span{ ^ l : X = X l }, U ¹ = { и е U : ( и,ф^ = 0, X = X l }.

Возьмем произвольную точку и е U, тогда и = афl + v, где v = Ри е U 1, а е R. Точка и еЕ точно тогда, когда выполнено

ay ы ? _3№

( ь        a Л

J vф2 dx +— + v,      e)

1 ^b

—J v ² ф > dlx = 0.

a

Введем в рассмотрение функционал 5 : U ¹ ^ R:

b

5 ( v ) = (J v ф l² dx

a

⁺ в ⁾² "I ^ф ^W J v^ a

и построим множества

U + ={ v е U ¹: 5 ( v ) > 0}, U - = { v е U ¹: 5 ( v ) < 0}.

Возьмем точку v е U + , тогда уравнение (34) имеет два решения

a

II ^фА\ь₃ ( Q )

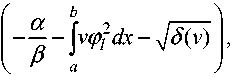
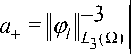
а Г 2 т .

—- wdx +

к

ь                 Л a               )

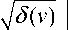
Построим множества

Е _{+ (} - ) ={ и е U : и = a _+н ( v ф + v , v е U + }.

Теорема 4.5. [35] Пусть а , ве R \{0} и

• (i)    X ^ { X k }. Тогда фазовым пространством уравнения (33) является все пространство U .

• (ii)    Xе { X k }. Тогда фазовым пространством уравнения (33) является множество Е ₊ иЕ - , каждая компонента которого Е ₊ и Е - биективно проектируется на множество U + .

Перейдем к рассмотрению задачи Шоуолтера-Сидорова-Дирихле

( X -А )( и ( x ,0) - и ₀( x )) = 0, x е ( a , b ); и ( a , t ) = и ( b , t ) = 0, t е R.                (35)

Теорема 4.6. [35] При любых а , ве R \{0} и

• (i)    Xе R \ {-Xk} существует точно одно решение задачи (33), (35) при любых и₀е U .

• (ii)    Xе {-Xk} существует два различных решения задачи (33), (35) при любых и₀е U таких, что Ри₀е U+.

• (iii)    Xе {-Xk} не существует ни одного решения задачи (33), (35) при любых и₀е U таких, что Ри₀е U-.

4.3.    Уравнение Бенжамина–Бона–Махони на графе

Замечание 4.3. В работе [4] была исследована неединственность решения задачи Шоуолтера-Сидорова для модели Плотникова.

Пусть G = G(V ; E ) - конечный связный ориентированный граф, где V = { V i } M 1 - множество вершин, а E = { E j }^ ^ _, - множество дуг. На графе G рассмотрим уравнения

^{( X -} Л )) ^u jt ^{+ u} j1xx = ^u j ^u jx ^{-v u} jxx ⁺ £ ^u j ,                              ⁽³⁶⁾

каждое их которых служит одномерным аналогом системы уравнений Осколкова и является гибридом уравнений Бенджамина-Бони-Махони и Бюргерса и моделирует длинные волны в

Манакова Н.А.,                            Неклассические уравнения математической физики.

Свиридюк Г.А.             Фазовые пространства полулинейных уравнений соболевского типа диссипативных и дисперсных средах. Для уравнений (36) в каждой вершине графа зададим условия uj (0, t) = uk (0, t) = um (lm, t) = up (lp, t),                                 (37)

E d j U jx (0, t ) - £ d m U mx ( l m , t ) = 0,                              (38)

jm где Ej,Ek e Ea(Vi), Em,Ep e E®(Vi), te R. Здесь через Ea(®)(Vj) обозначено множество дуг с началом (концом) в вершине V4.

Для редукции задачи (36)-(38) к уравнению (2) введем в рассмотрение гильбертово пространство L2(G) = {g = (g 1,g2,...,gj,...):gj e L2(0,lj)} со скалярным произведением lj

• < g , h >= E ^d j J g j ^{( x} ) h j ^{( x} ) ^dx .

Ej e E 0

Положим U = {u = ( u 1 , u ₂,

...,

Uj,...): Uj e W2(0, lj) и выполнено условие (37)}, а через F обозначим сопряженное пространство к U относительно скалярного произведения < •, • >. Формулой l j

< Au , v >= E d j J ( U jx ( x ) V jx ( x ) + Л ₀ U j ( x ) V j ( x )) dx , Л ₀ > 0, u , v e U ,

Ej e E 0

зададим оператор, определенный на пространстве U. Спектр оператора A вещественен, дискретен, конечнократен и сгущается только к +^, а его собственные функции образуют базис в пространстве L2(G) [1]. Обозначим через ф0 первую собственную функцию, отвечающую первому собственному значению Лу, а через {Лк}^=1 обозначим семейство остальных собственных значений оператора A, занумерованное по неубыванию с учетом их кратности; через {%.} обозначим соответствующие ортонормированные в смысле L2(G) собственные функции. Формулами L = A - Л, M = v(Л0 - A) + £ зададим операторы L,M : U ^ F. Далее формулой lj

< N ( и ), v ) = - E d j J U j U jx V j dx

Ej ^e E 0

зададим оператор N : U ^ F .

Лемма 4.2. [37]

• (i)    При всех £ , Л , Л ₀, v e R операторы L , M принадлежат L (U;F), причем, если | £ | + 1 Л о 1> 0, то оператор M является ( L , 0)-ограниченным.

• (ii)    Оператор N принадлежит C ” (U;F ).

Построим подпространство U1 = {u e U :< u,ф0 >= 0} и множества lj

S _{+ (} - ) = ^{{ u e} U 1 : E ^d j J ^{( u} jx ^{- £} ) ^dx >^0}.

Ej e E 0

Теорема 4.7. [37] При любых v e R \ {0}, Л 0 e R ₊ фазовым пространством задачи (36) - (38) является

• (i)    пространство U , если Л e (0, Л 1 ) \{ Л 0 };

• (ii)    C ” -банахово многообразие Е = Е ₊ иЕ — , моделируемое подпространством U 1 , любой атлас которого эквивалентен атласу из двух непересекающихся карт, если Л = Л 0 .

Замечание 4.4. В теореме 4.7 показано, что фазовым многообразием задачи (36)-(38) является C ” -банахово многообразие, однако многообразие не является простым и состоит из двух непересекающихся компонент.

Математика