Неколичественное протекание реакции как источник погрешностей втитриметрии
Автор: Голованов Владимир Иванович
Журнал: Вестник Южно-Уральского государственного университета. Серия: Химия @vestnik-susu-chemistry
Рубрика: Аналитическая химия
Статья в выпуске: 31 (207), 2010 года.
Бесплатный доступ
Критически рассмотрены известные в литературе по аналитической химии характеристики неколичественного протекания реакции, которые называют «степенью протекания реакции». Установлена связь этих характеристик с широко используемым в химической термодинамике и кинетике критерием (степенью) завершенности химической реакции и его безразмерным аналогом - степенью глубины реакции. Показано, что различные характеристики протекания реакции строят на основе разных способов сравнения степеней глубины протекающих в одинаковых условиях обратимой реакции и гипотетической необратимой реакции той же стехиометрии. Показано, что характеристики неколичественного протекания реакции, взятые сами по себе, без указания на метод отыскания точки эквивалентности, не могут быть предикторами погрешности титриметрического анализа. Предложена нормализованная запись ЗДМ для обобщенной реакции, которая позволяет классифицировать реакции на основе теории подобия и облегчает анализ зависимостей критериев неполноты реакции от степени оттитрованности.
Погрешности титриметрии, степень завершенности реакции, степень протекания реакции, степень глубины реакции, теория подобия
Короткий адрес: https://sciup.org/147160171
IDR: 147160171 | УДК: 543.08+543.422.7
Текст обзорной статьи Неколичественное протекание реакции как источник погрешностей втитриметрии
Проблема возникновения погрешностей при титриметрии из-за неколичественного прохождения реакции, по-видимому, впервые была сформулирована в известной монографии Шарло (с дополнениями Ю.Ю. Лурье) [1, с. 263]. Там же встречаем термин «степень протекания реакции». Термин находим в подписях к рисункам на с. 265 и далее редко по тексту. Термином «степень протекания» авторы скорее обозначают понятие, а не физическую величину. Создается впечатление, что авторы приводят краткую форму термина, опуская важный для понимания терми-ноэлемент. А это противоречит современным терминологическим стандартам [2]. Можно думать, что полной формой термина должно быть словосочетание «степень неколичественного протекания реакции» или «степень количественного протекания реакции». Заметим, что современные терминологические стандарты указывают на то, что применение диаметрально противоположных терминов должно быть резко ограничено. Поэтому следует отдать предпочтение только одной из названных выше характеристик неполноты реакции. Содержание понятия «степень протекания реакции» в [1] раскрывают на рис. 139 и 142, а также в формулах на с. 263 и 264. Откуда становится ясно, что безразмерная величина 0<ех<1, как количественная мера неполноты реакции, имеет смысл степени неколичественного протекания реакции. Получены уравнения связи между £х и степенью оттитрованности для систем с одной химической реакцией, т. е. для простых симметричных реакций.
Термин «степень протекания реакции» получил распространение в работах по титриметрии последнего времени [3-6] и списках литературы к ним. Здесь также используют неполную форму термина, однако, уже в смысле количественного протекания. В [5] отмечают, что «термин «степень протекания реакции» в целом неоднозначен». Иначе, разные понятия или разные величины называют одинаково. Такое состояние вопроса нельзя считать удовлетворительным и оно требует разрешения. К сожалению, авторы названных работ не поясняют происхождение термина.
Как будет показано в дальнейшем, авторы [3, 4] вкладывают в термин «степень протекания» смысл, диаметрально противоположный [1]. По определению [3, 4] размер степени протекания ре акции «показывает, какая часть анализируемого вещества вступила в реакцию в точке эквивалентности». Если в [1] исследуется влияние неколичественного протекания простых реакций на погрешность анализа, то в [3, 4] этот подход распространен на случай сложных реакций титрования.
В [6] дано новое, отличное от [1—4], определение степени протекания реакции: «...степень протекания реакции - отношение реального уменьшения концентрации А [титруемого вещества] за счет взаимодействия с титрантом (АА) к максимально возможному при данном f [степени от-титрованности] значению ДА, достигаемому при К -»со [константе реакции титрования]: т = АА/ААтах». Исследованы зависимости т от f для случая простой реакции титрования с произвольной стехиометрией.
Несмотря на различия между [1-4] и [6] в выборе характеристик неполноты протекания реакции, общим у двух этих подходов является то, что количественное описание протекания реальной аналитической реакции строят на её сравнении с прохождением идеальной, с точки зрения точности титриметрического анализа, гипотетической необратимой реакции той же стехиометрии. Общие черты имеют также уравнения связи критериев количественного прохождения аналитической реакции со степенью отгитрованности. И в том и другом случае приходят к записям нормализованных уравнений закона действующих масс (ЗДМ). В этих записях можно узнать объекты, изучаемые методами теории подобия [7].
Основной целью данного сообщения является выяснение общности и различий между названными подходами к проблеме теоретической оценки точности титриметрических методов анализа с использованием представлений о неколичественном протекании простых реакций. Анализ строится на основе общих принципов химической термодинамики и химической кинетики, а также с привлечением основных положений теории подобия.
Нормализованный закон действующих масс как основа для анализа функций неколичественного протекания реакции титрования
По нашему мнению, именно представление ЗДМ простой реакции в нормализованной форме [1,6] является ключевым моментом при построении функций неколичественного (количественного) протекания реакции. Поэтому наш анализ начнем с нормализации ЗДМ для реакции, записанной уравнением в общем виде [8, 9]:
^ГаД^ЬД. (1)
i i
Анализ будем строить на основе метода Де Донде (Th. De Donder) [8, 10], который в настоящее время является общепринятым при описании стехиометрических и балансовых отношений компонентов систем с химической реакцией. Согласно принципу Де Донде, в системе с химической реакцией независимым является только один участник реакции, что позволяет ввести единственную переменную £ = -Ащ /а; = Anj /bj, которую рекомендовано называть степенью завершенности (законченности) реакции [11]. По предложению Земански (M.W. Zemansky) [12], нормированную по исходному количеству вещества того или иного реагента величину ^/п, называют степенью глубины реакции. С другой стороны, известные исходные количества компонентов реакции можно выразить через мольные отношения и количество одного из реагентов, например компонента с i = 1: n° = f,n°; п° =0. Полагаем, что продукты реакции Bj в исходном растворе отсутствуют. Это допущение не меняет сути конечных выводов, а только упрощает представление их результатов. Тогда для равновесных количеств вещества компонентов реакции справедливы выражения:
n, -n^f.-a,^), 0, л nj = n^j^l), где г)] = Е,/п° - степень глубины реакции по выбранному ведущим компоненту.
Перейдем от количеств веществ к их концентрациям:
[АД-с^ -а^) [АД/^ = d-^fj -а^Д
, или , (3)
[ВД^с^цД [BjJ/cj ^d-’bjp,)
где d = LV/Vi - коэффициент разведения раствора первого реагента при добавлении к нему всех прочих реагентов.
Подставим выражения (3) в уравнение ЗДМ для реакции (1) и приведем левую и правую части этого уравнения к безразмерному виду. Получаем уравнение ЗДМ в нормализованной форме
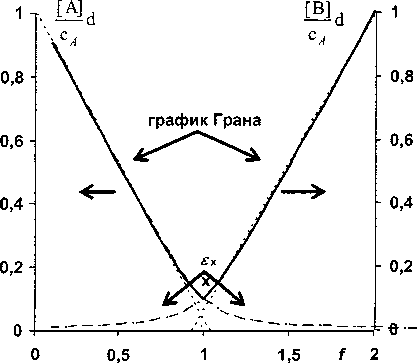
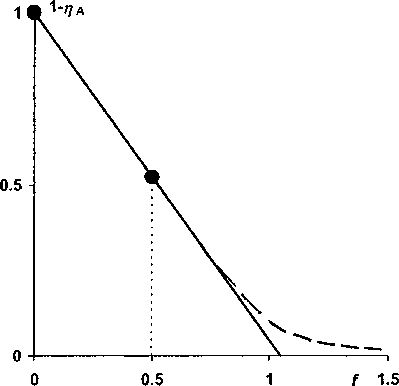
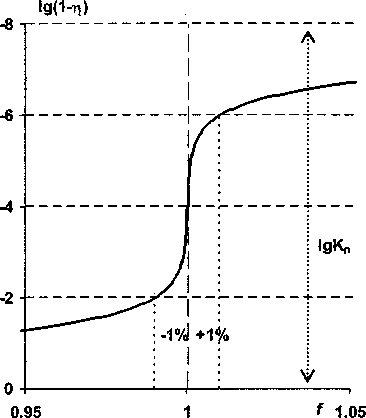
Кпд=Ксра' ^^^ПЬ] ' =d^a,-^bj^PJO j i Исходя из теории подобия [7], выражение в левой части равенства (4) является критерием подобия, а переменные £, тр и d - это инварианты подобия. Критерий подобия Кпд, а также f, и d -определяющие критерии, а переменная г] i - неопределяющий критерий. Неопределяющий критерий глубины реакции можно вычислить, задавая численные значения определяющих критериев. Заметим так же, что выражение в левой части (4) является одночленом степени р = Еа; - ХЬ,. Поэтому обратимую реакцию при равновесии можно также как одностороннюю реакцию [9] характеризовать её порядком р. Несложно показать, что коэффициент разведения также является простой функцией от переменных £: d = 1 + £~-H =1 + £xifi>( i=2 cii=2 где c° и c° - концентрации смешиваемых растворов реагентов. Поэтому, в конечном счете, в уравнении (4) инвариантами подобия являются мольные отношения Xj, f; и гц. Если все реагенты взяты в эквивалентных количествах, т. е. f; = a;, a d = 1, тогда кпд=п^ПаГа,(1-ПзкГа1-(6) i Критерий подобия можно однозначно выражать через степень глубины реакции в отсутствии избытков реагентов (в точке эквивалентности), что в ряде случаев предпочтительнее [3], поскольку 0 < т)эк < 1. Применяя теорему Кирпичева-Гухмана [7] к нормализованному ЗДМ, можно заключить, что степень глубины реакции как функция fj будет одной и той же для реакций одного порядка при фиксированном значении критерия подобия Кад, а также постоянстве коэффициентов \. Эту функцию назовем функцией глубины реакции по компоненту Аь Очевидно, что для реакций одинаковой стехиометрии можно построить не один, а несколько взаимозависимых критериев подобия; для этого достаточно перенумеровать реагенты в уравнении реакции. Можно видеть, что (4) в сочетании с (3) позволяет рассчитать нормализованные по щ распределительные диаграммы, аналогичные [13]. Нормализованные кривые титрования будут частными случаями таких диаграмм. Отметим, что принципы подобия используют при изучении комплексообразования по способу подбора и совмещения кривой [14]. Перспективность применения нормализованных уравнений ЗДМ для реакций экстракции показана В.И. Кузьминым [15]. Уравнения (2)-(6) при количественном описании кривых титрования существенно упрощаются. Порядок реакции понижается, поскольку, как правило, концентрации всех вспомогательных реагентов поддерживают на постоянном уровне и не включают в уравнение реакции, полагая их компонентами фона. Концентрации фоновых веществ в степенях соответствующих стехиометрических коэффициентов входят в значение условной константы равновесия в качестве сомножителей. В уравнении реакции оставляют только два реагента: титруемое вещество Ai и титрант А2. При этом (4)™(6) принимают вид: Кпд -d^’-^nPxi-a^F^^(7) d = l + ^f,(8) С2 Кпд =а^аГ211э?Ч1-Пэк^(9) где f- степень оттитрованности. Взаимосвязь между различными характеристиками неколичественного протекания реакции титрования Используя принцип Де Донде, можно сравнивать реакции по степеням их завершенности ^ (или по степеням глубины т|) при одинаковых граничных условиях. На это важное обстоятельст- во ранее, по-видимому, не было обращено внимание. В теоретическом плане полезно сравнивать функцию глубины конкретной реакции с аналогичной функцией для гипотетической реакции. Причем вид функции для гипотетической реакции с очевидностью известен. И в испытуемой, и в стандартной реакции участвуют одни и те же вещества в тех же количествах, но условия осуществления реакций таковы, что первая протекает неколичественно, а вторая количественно (имеет предельную глубину Птах)- Обе реакции рассматривают в условиях равновесия системы. Очевидно, что испытуемая реакция - это обратимая реакция, а стандартная, как предельный случай, абсолютно необратима. Придадим этим рассуждениям количественное выражение, записав соотношения: ах = ^Imax ~ Л 5 Т = П/т]тах’ И^-Отах^ПтахН-П/Птах =1-Т-О Здесь мы фактически исчерпали все возможные способы сравнения значений глубины обратимой и необратимой реакций. Правая часть уравнения (10) является определением степени неполноты протекания реакции, введенным в [1], но другим способом. Уравнение (И), по сути, не отличается от определения степени количественного протекания реакции в [6]. Однако наше определение обладает большей общностью и не требует привлечения других вспомогательных переменных, которые используют в [6]. Исходя из логического обоснования т (И), эту функцию правильнее называть степенью необратимости реакции, а е = 1 -т - степенью обратимости реакции. Важно заметить, что разные измерители неколичественного (количественного) протекания реакции однозначно выражаются друг через друга. Для необратимой реакции степень глубины как функцию от f легко найти из уравнений (3): Tlmax=a2lf При£<1 И Лтах=а^ При£>1.(13) Нормализованные уравнения кривых титрования в случае необратимой реакции имеют вид: [АД/c^l- —f при£<1 и [АД/с^О при£>1,(14) а2 [A2]/cj=0 при£<1 и [A2]/Cj=f-— при£>1,(15) а1 Ь;Ь: [В:)/С] =—f при£<1 и [В:]/С] = — при£>1.(16) а2 Каждое из этих уравнений описывает кусочно-гладкую функцию с особой точкой при £= а2/аь Уравнениям (10)—(12) также несложно придать конкретную форму с учетом выражений (13). Продемонстрируем развитую здесь теорию на примере реакции титрования А + В = С1, рассмотренной в [1], при d = 1. Из уравнений (3), (4) и (6) имеем: [А]/са=1-т]а и [В]/са=£-Ла,(17) квд = КС2 = (1 -TiAFVf-Па)-1 =(1-ПэкГ2-(18) Эти уравнения являются уравнениями линейных кривых титрования, записанных в параметрической форме. Каждую кривую удобнее представить одним нормализованным уравнением: [А]/са = 1 — т]А = 1— f + К^(1 — т]А)-^,(19) [В]/сА -£-Ла -f-l + C(f-nAr' -(20) Нормализованные уравнения кривых титрования в случае необратимости реакции имеют вид: [А]/са=1-£ при£<1 и [А]/са=0 при£>1,(21) [В]/сА=0 при£<1 и [В]/сА = £-1 при £ > 1.(22) Каждое из этих уравнений является кусочно-гладкой функцией с особой точкой при £= 1. Из сравнения уравнений (19) и (20) с уравнениями (21) и (22) видим, что функцию ех„ определенную (10), можно получить, вычитая из реальной кривой титрования гипотетическую кривую. Такое определение 8Х позволяет, в принципе, измерять степень неколичественного протекания не только простой, но и сложной реакции титрования. Выражая в уравнении (18) т]А через т|1пах и sx или через r]max и т, получаем уравнения, не отличающиеся, с точностью до обозначений, от уравнений в [1] и [6], соответственно: KcA = (!-£ + sx) 'е*1 при£<1; KcA =(f-l + sx) 1sx1 при£>1, КсА =(1-£т)-1(1-т)-|£-1 при£<1; KcA =(1-r)-1(f-т)-1 при£>1. Исходя из определения (12) запишем также функцию: (23) (24) KcA =(l-f+ fs)-I(fe)-1 при£<1; КсА = E-1(f-1 + s)-1 при£>1. (25) Из сравнения (23) и (25), а также из сопоставления (24) с (18) видим, что ех = е и т = р при £ > 1. При £ < 1 эти характеристики реакции существенно различаются. Рис. 1 иллюстрирует отмеченные различия на примере двух, рассмотренных в [1] реакций. Рис. 1. Степень обратимости (сплошная линия) и степень неколичественного протекания реакции (пунктир) в зависимости от степени оттитрованности для реакций А + В = Ci (а) и А + В = С (б) при т]Эк = 0,9 Из рис. 1, б видим, что разница между реальной кривой и идеальной кривой титрования убывает с уменьшением f практически до нуля. Вместе с тем степень обратимости реакции хотя и убывает, но не столь стремительно. Для случая (рис. 1, а) степень обратимости даже увеличивается и при f = 0,01 реакция практически не протекает, поскольку s = 1 (т = 0). Этот результат легко объясняется известными представлениями о произведении растворимости. Этими же соображениями объясняется характер изменения ех при £ < 1. Величина е как показатель обратимости более чувствительна к дефициту титранта по сравнению с sx. С другой стороны, показатель ех, по-видимому, более полезен в практическом плане, поскольку лучше характеризует близость реальной кривой к идеально линейной кривой титрования. Возрастание показателей обратимости при приближении слева и справа к точке эквивалентности просто объяснить с точки зрения теории сдвига равновесий, например эффектом общего иона. Легко убедиться, что особые точки на рис. 1 являются точками пересечения кривых титрования, которые описывают уравнения (19) и (20). Это положение иллюстрирует рис. 2. Из рис. 2 видим, что линейные кривые титрования разделяются в точке пересечения на ветви графика Грана (жирные линии) и функцию ех (нижние пунктирные ветви кривых), см. также уравнение (23). Уравнение двухстороннего нормализованного графика Г рана записывается выражением Рис. 2. Взаимосвязь между нормализованными кривыми титрования и функцией неколичественного протекания реакции А+В = Ci при т]3к = 0,9 ..f[A])vA+VB . , , antlg • —----~l-f при£<1; I CA J VA [B] vA+vB „ 1 , — • —---— ~ f -1 при f > 1. caJ VA * Эта запись означает то, что функцию Грана (приведена слева от знака равенства) аппроксимируют идеальной кривой для полностью необратимой реакции. Очевидно, что распределительная диаграмма, взятая в целом, содержит больше информации о равновесии, чем ее части. Отсюда возникает вопрос о целесообразности вычислений только функций протекания реакции 8Х или т по уравнениям (23) и (24). Неполноту реакции достаточно характеризует степень глубины реакции т|д, см. уравнения (19) и (20). Вместе с тем представления об обратимой и необратимой реакциях являются теоретическим обоснованием метода линейной аппроксимации реальных кривых титрования и позволяют детализировать участки этих кривых (см. рис. 2). О прогнозировании погрешности с использованием показателей неколичественного протекания реакции титрования В монографии [1] изложение теории возникновения погрешностей в титриметрии из-за неко личественного прохождения реакции построено не совсем удачно: так, что может создаться впечатление о независимости погрешности от способа установления точки конца титрования (т.к.т.). В качестве примера в [1] рассмотрено возникновение погрешности при аппроксимации кривой титрования прямой линией, проведенной через две точки. Именно для этого метода рассчитаны погрешности, которые приводят в табл. 34 на с. 263 [1]. В соответствии с методом [1] верхнюю ветвь нормализованной кривой титрования на рис. 3 приближаем прямой, проведенной через показанные на графике точки. С использованием уравнения прямой через две точки или из подобия треугольников выразим погрешность определения 5 = f - 1 через измерители неполноты реакции Рис. 3. Отыскание погрешности при аппроксимации кривой титрования для реакции А + В = Ct прямой, проведенной через две точки. = 0,9 Очевидно, что для оценки погрешности можно обойтись без переменных sx и т. Достаточно знать координаты узловых точек (0,1) и (f*, 1—т|*) на нормализованной кривой титрования. Заметим, что, применяя глазомерный метод установления т.к.т. по инструментальным кривым титрования, реперные точки для аппроксимации выбирают, анализируя форму кривой в целом. Поэтому наверняка не будет выбрана в качестве узловой точка при £ > 1, если получена подобная рис. 3 кривая титрования Вычисление погрешности для таких случаев, как это делают в [1, 5], вряд ли оправдано. Кривые, приведенные на рис. 2 и 4, являются еще одной иллюстрацией тезиса о том, что характеристики неколичественного протекания реакции, взятые сами по себе, без указания на метод отыскания т.к.т., мало что говорят о погрешности анализа. Если точку эквивалентности находят по двум точкам на одностороннем графике Грана (см. рис. 2) тогда как для дан ного примера, возможно либо завышение результата анализа на 5 = 4 % (левый график), либо его занижение на 5 = -4 % (правый график). При использовании двухстороннего графика погрешность анализа не выйдет за пределы -4 % < 8 < 4 %. При использовании метода скачка на логарифмической кривой титрования для отыскания т.к.т. (рис. 4), характер погрешностей такой же, как для двухстороннего графика Грана. Нормализованную логарифмическую кривую титрования получим из уравнения (19) после логарифмирования его аргументов: 20ig(l—На)= J _f _|_ ]Q *§н ^а) ^Кпд Погрешности анализа находятся в пределах: _1O|sO^a) Видим, что ни ех, ни т не входят, непосредственно, в уравнение (29). Выполненный здесь анализ погрешностей не отличается от приведенного в [16], где термин «степень протекания реакции» не используют. Вместе с тем логическим обоснованием метода скачка являются представления о разрывной функции. Функция с разрывом получается из уравнения (21) после его логарифмирования. Исходя из метода подобия, полученные выше результаты по прогнозированию влияния неколичественного протекания реакции А + В = СI на погрешности анализа, обладают высокой степенью общности и их можно переносить на подобные объекты. Например, одинаковыми будут индексы крутизны, величины скачков и некоторые другие характеристики подобных кривых титрования (рис. 4) для веществ с перечисленными ниже константами и концентрациями: Рис. 4. Нормализованная логарифмическая кривая титрования для реакции А + В = С; при 1дК„д = 8 рк5 Ige 12 14 -2 -3 Многие, но далеко не все, реакции титрования относятся к рассмотренным здесь простым реакциям. Некоторые сложные реакции, такие как реакции комплексонометрического титрования, можно свести к простым, задавая на постоянном уровне pH раствора. Тогда как титрование слабой кислоты - это сложная, несводимая к простой, реакция. Титрование смесей веществ также можно считать сложной реакцией. Развитый здесь и в работах [1—6] подход вряд ли, в общем случае, применим к сложным реакциям, из-за неоднозначности и трудности выбора стандартной односторонней реакции. Заключение Предложена нормализованная запись ЗДМ для реакций титрования, которая позволяет классифицировать реакции с точки зрения теории подобия. Показано, что принцип Де Донде и связанное с ним понятие степени завершенности реакции можно использовать для сравнения завершенностей различных реакций и, прежде всего, завершенности гипотетически полностью необратимой и завершенности реальной обратимой реакций титрования. Выведены уравнения, устанавливающие взаимозависимости между различными, известными в литературе, показателями неколичественного протекания реакции. Показано, что при прогнозировании погрешности титрования, возникающей из-за неколичественного протекания реакции, достаточно использовать только одну величину - степень завершенности реакции или её безразмерный аналог - степень глубины реакции. Автор благодарит профессора В.И. Вершинина за полезную дискуссию.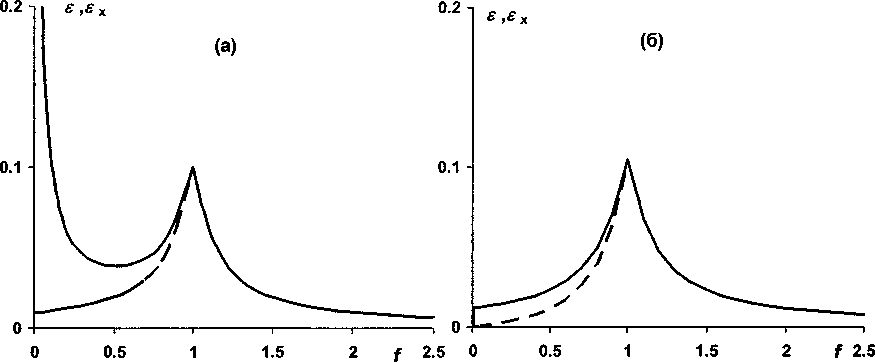
Список литературы Неколичественное протекание реакции как источник погрешностей втитриметрии
- Шарло, Г. Методы аналитической химии/Г. Шарло; под ред. Ю.Ю. Лурье. -М.; Л.: Химия, 1966.-Ч. 1.-975 с.
- Чертов, А.Г. Физические величины/А.Г.Чертов. -М.: Высшая Школа, 1990. -335 с.
- Титриметрические методы анализа неводных растворов/под ред. В.Д. Безуглого. -М.: Химия, 1986.-384 с.
- Худякова, Т.А Кислотно-основные свойства электролитов и критерии их анализа/Т.А. Худякова, П.М. Арбатский. -М.: Химия, 1988. -64 с.
- Вершинин, В.И. Расчет степени протекания реакции в точке эквивалентности и использование подобных расчетов в титриметрическом анализе/В.И. Вершинин//Журн. аналит. химии. -2003.-Т. 58, №11.-С. 1133-1139.
- Вершинин, В.И. Изменение степени протекания реакции в процессе титрования/В.И. Вершинин, Г.П. Кукин//Журн. аналит. химии. -2004. -Т. 59, № 2. -С. 125-134.
- Батунер, Л.М. Математические методы в химической технике/Л.М. Батунер, М.Е. Позин. -Л.;М.:ГХИ, 1953.-448 с.
- Мюнстер, А. Химическая термодинамика/А. Мюнстер. -М.: Мир, 1971. -295 с.
- Эммануэль, Н.М. Курс химической кинетики/Н.М. Эммануэль, Д.Г. Кнорре. -М.: Высшая школа, 1969. -432 с.
- Пригожий, И. Химическая термодинамика/И. Пригожий, Р. Дэфей. -Новосибирск: Наука, 1966.-509 с.
- Степин, Б.Д. Применение международной системы единиц физических величин в химии/Б.Д. Степин -М.: Высшая Школа, 1990. -96 с.
- Zemansky, M.W. Heat and Thermodynamics/M.W. Zemansky-2-nd. -N-Y, 1943. -p. 325 (цитировано по [10]).
- Батлер, Дж. Ионные равновесия/Дж. Батлер. -Л.: Химия, 1973. -448 с.
- Россотти, Ф. Определение констант устойчивости и других констант равновесия в растворах/Ф. Россотти, X. Россотти. -М.: Мир, 1965. -564 с.
- Кузьмин, В.И. Автореф. дис.... д-ра хим. наук/В.П. Кузьмин. -Красноярск: ИХиХТ СО РАН, 2002. -42 с.
- Янсон, Э.Ю. Теоретические основы аналитической химии/Э.Ю. Янсон, Я.К. Путнинь. -М.: Высшая Школа, 1980. -260 с.


