Некоторые алгебраические аспекты метода системного анализа в общей теории сложных механических систем

Пусть малые колебания сложной механической системы (СМС) вблизи устойчивого положения равновесия представляются обыкновенной дифференциальной системой вида:      ■

^q + ^q + 4q = F^,                       (1)

где q - вектор-столбец лагранжевых либо динамических [1, 2] обобщенных координат (5_Р q₁,.„,q_s), характеризующий обобщенное перемещение; F- вектор - столбец возмущающих функций, характеризующий действие внешних сил, который также рассматривается как обобщённый, в общем случае зависящий от обобщенных координат, обобщённых скоростей, обобщенных ускорений и времени; 4г =[^1, 4> =[^су1 (^>7 = 1>^S) - матрицы инерционных и квазиуп-ругих коэффициентов; 4 = [^1(^7 = 1,5) - матрица диссипативных коэффициентов, удовлетворяющая определенным частным условиям [3-6].

Анализ и синтез процессов, описываемых системой дифференциальных уравнений (1), особенно если дифференциальная система имеет высокий порядок, связаны с преодолением немалых трудностей. Эти затруднения в значительной мере могут быть сняты, если предварительно соответствующей заменой переменных привести исходную систему к виду, матрицы коэффициентов которой имеют диагональную или квазидиагональную форму. Обычно такие преобразования проводят на простейшей системе вида

4q*M = F^tY(2)

которую проще привести к независимым уравнениям, чем исходную (1). Кроме того, система (1), путем исключения из нее слагаемого, содержащего q, с помощью замены переменных q=^y>(3)

где ф = exp (-1/2 4"’4 0(4)

- квадратная матрица, всегда может быть приведена к виду, аналогичному (2), за исключением того, что коэффициенты преобразованной системы будут уже функциями времени:

у + Р(0у = 3(0,(5)

где р(/) = ф"1[^2"14) -l^-^-^ )2]ф, 50 = ф’%“1/’(?).

Рассмотрим один из алгоритмов таких преобразований (7) на примере системы, дифференциальные уравнения движения которой имеют вид

4q + ^ + ®)v40q = F(t),(6)

где у = 1, ае = о— в случае вязкого трения и у = §, ае = z£ в случае частотно-независимого трения, dt a a - коэффициент пропорциональности (коэффициент внутреннего трения) [3-4, 6, 8].

Положив в (6) Р$ ⁼ 0, получим однородную систему

45+(у+ае)4,9 = О,                             (7)

решение которой представим в виде q^^exp^tY                    (8)

где ц/⁷⁾ - вектор амплитуд обобщённых координат q_} при колебаниях системы с собственной частотой и*, совпадающий с точностью до постоянного множителя с вектором коэффициентов распределения амплитуд соответствующей консервативной системы. В силу того, что матрица А^Д, имеет простую структуру, подстановка (8) в (7) преобразует последнее в систему вида:

-4^w‘+4,^=о,                        (9)

где W* =Jzag|(2,(o‘)²,..^ K=dtag^^sYY^*i®\Y-^

ж^ = ого * для вязкого трения и ае* = В для частотно-независимого трения, j = 1,5.

Используя преобразование q = Т • q приводим неоднородную систему (6) к форме

Умножая слева обе части этого уравнения на транспонированную матрицу Ч*ти используя соотношение (9), предаем уравнению вид

Т^т ^q + (у + ae)^¹^ YW*A⁴^ = Ч^Р^,               (10)

в котором матрица Ч^АА = 4 является диагональной с элементами, определяемыми формулой

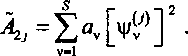
Сопоставляя характеристические уравнения диссипативной

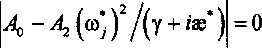
и

консервативной |4, -^(Ву| = О систем замечаем, что (со*) Ду + zae*) = со7, откуда вытекает следующее тождество: W*A-1 = diag^to2,to22,... ,со^ = W, а уравнение (10) принимает вид я'чДу + ав^^Ч'^).                 (11)

Следовательно, неоднородная система (21), также как и (2), преобразуется к системе S - несвязанных между собой уравнений

^.+(у + ав)(о^.=4У,                             (12)

где d_jr = ——; З_у (/) = £ vV^r (О ^_ Р^я обобщенная сила j-й формы колебаний системы.

В случае учета демпфированная по гипотезе вязкого трения, когда линейный диссипативный оператор 4 такой, чтоаесо^у = G<$?’_jq_j = 2s_y5,, где е - коэффициент демпфирования [3, 5], уравнение для у-й обобщённой координаты #_у системы (12), принимает вид

5j ^{+ 2e}j5j + ®>4 = djr ,                                (¹³)

Использование преобразования (3) с учетом (4) приводит (13) к виду

4+^4=еЕЧ>                 04)

где егЕ = (со2 - Еу) - собственная частота колебаний диссипативной системы.

Обозначив правую часть (14) e*7'^ через Зу (?) и опустив индекс/, получаем одно уравнение второго порядка вида y + to2y = 3(?).(15)

В том случае, когда ю2 - е2 > 0, общий интеграл однородного уравнения y + to2y = 0,(16)

может быть представлен в виде

У = q cos ю8? + с2 sin to8? = c^ (?) + c2y2 (?),(17)

где ci и C2 - произвольные постоянные, а фундаментальная система решений однородного уравнения yi(f) и уг(?) - гармонические функции.’

Решение неоднородной системы (15) будем искать методом Лагранжа. Для этого положим у = Аут+Ву2, у = Ауг+Ву2,(18)

где Л и В - некоторые неопределённые функции времени, подлежащие определению.

Поскольку само дифференциальное уравнение (15) эквивалентно единственному соотношению между функциями у и 3, то ясно, что соотношения (18) будут справедливы только при условии их взаимной совместимости. Для установления этого факта дифференцируем первое из условий (18) и, приравнивая ко второму, получаем условие совместности системы (18)

А^+Ву₂=0.                            (19)

Далее, подставляя второе из условий (18) в уравнение (15) и учитывая (16), получаем iy1+^2=3(?).                            (20)

Поскольку решения у1(0,у2(?) образуют фундаментальную последовательность, то двух уравнений (18) и (20) достаточно для определения А, В через У1(?),уг(?) и 3(?). Поэтому решив систему уравнений (19) и (20)

Л^+^з-О, Ау_х*Ву₂=^

относительно неизвестных произвольных функций Л(?) и В (?), находим:

А = АЭДУ1,  В = "ЭДу„               (2D где определитель

Д=У1 У2 ,                                   (22)

на основании второго следствия теоремы Лиувилля [9] и того факта, что уравнение (15) не содержит первой производной - величина постоянная. Действительно, в рассматриваемом случае

COStog?

-ro8sinco8?

sin (ве?

= toe = const.

Имея это в виду, интегрируя систему уравнений (21), находим:

А =-- j3(?)sinm_E?t/?; В = — |з(?)со8©_е??.

а                ®е а

Подставляя значения Л и В в первое из условий (18), находим

1 y=—A ®_E

- cos tog? J5(?) sin +sin ©₈? j5 (?) cos ©₈?<й -

и, соответственно, для j-й главной координаты при подачи воздействия на r-й вход

s

cos®_jetdt-costo_jEt^e^J‘d_jr £ЛО) sinco_ysZrfZ >.

Заменяя под знаком интеграла букву Z буквой т, считая начальные условия нулевыми и полагая а = 0, после внесения под знак интеграла множителей, не зависящих от переменной интегрирования, получаем частное решение каждого из уравнений в виде:

5-^'1

^js О

S sincoye(z-T) XFr(T) dx,

где d_Jr = £ ^ L^L^av [v^]², а т - вспомогательное время интегрирования, изменяющееся в Г=1      / V=1

пределах от нуля до рассматриваемого текущего момента времени t. Зная qj, находим решение исходного уравнения (13)

9j

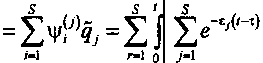
sinto^Z-T)^^.,, F_r^dx.

Полагая F, (z) = 7^ cos coz и интегрируя (27), получаем s ,, s s q.^^qj =EZ

Ms1,

cos

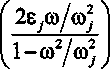
coZ-arctg

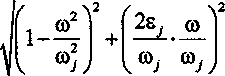
Рассмотренный выше метод решения дифференциальных уравнений имеет достаточно большую давность. Однако, несмотря на это непосредственное практическое его применение к решению технических задач, связанных с расчетом СМС наталкивается на ряд затруднений, в том числе связанных с самим преобразованием к главным нормальным координатам. Кроме того, используемое преобразование (10) не всегда приводит к желаемому результату. Так, например, в случае консервативных систем, данное преобразование работает отлично, а для диссипативных систем нормальные координаты существуют только при некоторых ограничениях, накладываемых на матрицы Л2, Л] и Ло [3, 5].Определенные затруднения в реализации метода возникают и в тех случаях, когда силы, передаваемые силовым полем, линейно зависят от смещений точек (частиц) СМС и любых производных этих смещений по времени. К числу таких полей можно отнести, в частности, поле давления сжимаемой или идеальной жидкости в гидродинамически линейных задачах гидроупругости, которые возникают при исследовании динамики СМС с полостями, частично заполненными жидкостью. В этих случаях метод главных координат, вообще говоря, не применим, поскольку формы колебаний оказываются связанными [2, 4, 9, 11, 12]. Предпочтительными оказываются интегральные методы. Приведение дифференциальной системы к интегральному уравнению является лишь изменением формы постановки задачи, хотя и обладает определенной спецификой. Пусть имеется линейное дифференциальное уравнение S-ro порядка

y^(s) (х) + а, (х)у^(М (х) +... + a_s (х)у^{0} (х) = F(x},                   (29)

где а, (х),..., +a_s ^uF^ - заданные непрерывные функции от х на рассматриваемом интервале изменения переменной.

Допустим, что начальные условия задачи, описываемой дифференциальным уравнением (29), определены для какого-либо значения аргумента х = а в виде следующих равенств:

у^ = С₀, У(а) = С„..„ Л¹\а) = С₅_₁.                 (30)

Решение уравнения (29) с начальными условиями (30) может быть сведено к решению интегрального уравнения Вольтерра второго рода

фМ + JK(^) ф(^)^=/ W •

Это делается следующим образом. Положим, что у($)=фМ-

Интегрируя обе части равенства (32), находим где Cs-1 - постоянная интегрирования, равная начальному значению (5-1)-й производной в точке а, принятой за начало отсчета. Интегрируя таким же образом равенство (33), получаем

v(s-i)_(7 *_- + с

У ^US-1 |  ^т^З-2

и т.д., в результате находим

/ _ x(S-l)        / _ \(3-2)                     х х it n. +C“ 1Л11 +-+C,*+C0+/..J ф©^8.      (34)

S раз

Используя тождество Дирихле XX           X ( иЧЙ”¹)

и возвращаясь к дифференциальному уравнению (29), видим, что его можно записать в виде (31), если положить:

V И > (^-1)! ’

/(х) — F^ ^^(х) (C_s_₁x + C_s_₂)a₂(x)

Обратно, решение уравнения (31) с К и/ определенными по формулам (35) и (36), будет эквивалентно решению задачи Коши для линейного дифференциального уравнения (29).

Аналогично тому, как линейное дифференциальное уравнение (29) с классическими начальными условиями (30) приводит к интегральному уравнению Вольтерра, это же дифференциальное уравнение при добавочных условиях на обоих концах х = 0 и х = L основного интервала (0, L\ приводит к интегральному уравнению Фредгольма [12-14]. Общий класс таких добавочных условий можно получить, потребовав, например, чтобы 8 линейных комбинаций 28 величин

у(0),У(0),...уч(0),у(£), у'^,. .-УЧ1}(37)

принимали заданные значения, то есть, чтобы

S-l                    S-1-

(38) т=0

где а^, и Ск - заданные постоянные.

Если С_о-С.=... = C_s__} = 0, то можно рассматривать однородные краевые условия

3-13-1

Z»™^ (0) = ЁР^У”’ (£) (к = 0,1,..., S-1).(39)

т=0т=0

Согласно общей теории интегральных уравнений [12-14] уравнение (29) вместе с краевыми условиями (39) называют системой Штурма-Лиувилля, которая эквивалентна интегральному уравнению Фредгольма второго рода с параметром 2:

ф(х) = А.|с(х,5) т(^)ф(^)^ + у(х), О

L где у(х) = Jg(x,^) F^dS, - заданная функция г, ф(^) - неизвестная функция; G^x,^ - функ-о ция Грина.

Существуют три различных метода решения этого уравнения. Один из таких - это метод развитый Гильбертом и Шмидтом, который выражает ^(х) через так называемые собственные функции, которые обыкновенно представляют собой решения соответствующего однородного уравнения получаемого из (40), полагая в последнем у(х) = 0:

ф(х)-ф(хЛ)«и)ф(0^ = 0.                 (41)

о

Однако, несмотря на то, что в (41) функция Грина G^x,^ симметрична, ядро G(x,^)m(^) этого уравнения, из-за множителя т^ , несимметрично, но его можно симметризировать, если обе части уравнения (41) умножить на ^т^ , что всегда допустимо, так как т^ положительно. Полагая

ф(х) = ^т^хУ^х^,    G(x,^ = G(x,^) ДхД9 = G(^,x),       (42)

получаем для новой неизвестной функции ф однородное интегральное уравнение Фредгольма второго рода с симметричным самосопряженным |G(x,^) = G(^,x)l ядром:

ф(х) = ф(х,$)ф(^,                    (43)

о в котором нас будет интересовать спектр собственных значений и собственные функции. Но это уравнение, вообще говоря, не имеет никакого решения, кроме тривиального: ф(х) = 0. Однако существует ряд чисел X,, X,,..., Хл,..., называемых собственными значениями; для каждого из которых, однородное уравнение имеет ненулевое решение, все они действительны и представляют собой квадраты частот свободных колебаний системы (Я = со2). Система, следовательно, может совершать периодические колебания не с любой частотой, а только с частотами, равными корням квадратным из характеристических чисел. При этом соответствующие фундаментальные функции ф1(х), у/2to,••.симметризированного уравнения и функциифл(х)= фл(х)/^т^ , дающие амплитуды колебаний точек системы образуют нормированную ортогональную систему в основном интервале (0, L) с характеристической функцией т(х), то есть удовлетворяют соотношениям

L                      L

0, я # v,

1, И = V.

К W Wv (s)^=Jw(^)

Считая, что задача о собственных колебаниях решена, функции ф_у (х) найдены - воспользуемся общей теорией метода факторизованных возмущений [17]. В частности, можно показать, что для непустого со - множество, такого, что для любого принадлежащего ему фиксированного значения со, найдется единственная функция 91 (х, %; со²) двух координатных переменных хи ^и одного комплексного переменного со, такая, которая определена на квадрате ^ х е [0, X]; е [О, X]; симметрична; удовлетворяетуравнению:

[^-оУЦ^Э^х, £;<в2) = 5(х-£)

и представима соотношением вида 9t(x,^co²

где 9?(х,£;со2) - частотная гриновская функция (ЧГФ); G^x,^) - обычная или обобщенная функция Грина статической задачи, она единственна, симметрична G^x, £) = G(£„ х) в вещественном случае ( G(x, §) = G(£, х) * в комплексном случае) и на квадрате (0 < х, Е < Z) вместе со своей производной ^G(x, £) непрерывна как функция двух переменных; Г(х, £; X) - резоль вента уравнения Фредгольма второго рода со статической функцией Грина G(x, ^) системы в качестве нагруженного ядра

r(x,^X)-XjG(x,z)r(^;X)/^)cZz = G^ ' ■      (47)

О

Функция 91 (х, ^; со2), при любом фиксированном и допускающем ее существование со, является гриновской функцией решаемой задачи, и, как все простые гриновские функции, совпадает с ядром интегрального представления обратного оператора задачи

[©(^■^[Л-шЧ]’1,                     (48)

и, в соответствии с теоремой Гильберта-Шмидта [13,14], представляется абсолютно и равномерно сходящимся рядом

91 (х, §; X) = G(x, §)+ ^.^W .                ₍₄₉₎

v=i X_V(X_V-X)

Принимая во внимание очевидное равенство Hm9l(x, £; X) = G(x,£), и известное соотношение

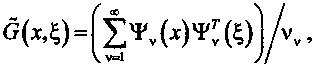
которое, в силу симметрии и положительности ядра G(x,^), сходится по теореме Мерсера [13, 14] абсолютно и равномерно при независимом изменении переменных в области (0 < х, ^ < Z), для всех X*Xv(v = l,2,...) и х, ^ е [0, Z], будем иметь матрицу

v=l Лу — Л

Полагая, что на вход системы подается внешнее воздействие / (х, с) = е""™*Р (х), где г - произвольное комплексное число (/ = >/-1, 1 6 (—°о, + °о)), а Р(х) — регулярная функция аргумента х и считая, что существует представление у (х, t) = е~^,ю,У (х) и возможен переход к частотной со - параметризованной (не содержащей времени /) задаче, решение задачи по определению комплекснозначных функций амплитуд вещественного переменного У(х), определенных на [О, Z] для каждого X * X_v, можно сформулировать в следующем виде [15]: Для любого правильного XuF найдется решение, причем единственное и представимое в виде:             '

У(х)=|91(хЛ;Х)Г(^^,                        (52)

О при этом оператор [р (со)] ’ обратим и справедливо тождество

[®W]" 8(х-У .Я(лЛ х) = у         .             (53)

v=l          Л

Доказательство тривиальное и получается подстановкой формулы гриновской функции в предполагаемое решение (52), то есть доказательство напоминает типичный прием решения дифференциальных уравнений: когда мы полагаем решение в определенном виде, а затем подставляем его в дифференциальное уравнение и убеждаемся, что последнее выполняется.

Если в формулах (53) и (52) заменить оператор вида [Р(ю)] ¹ — [^^ — со²^^] *Ha оператор [^’0®)]¹ =[Л-to^ + zco^J , a X_vHaX*=Z*X_v и, соответственно, G(o,^) на G(x,^) = Z*G^x,S^ , где Z* = y+zae - комплексное число, a Z* - комплексно сопряжённое число, то для диссипативной системы получим:

у*(х)= j9f(x,^;X)F*(^,(

О

На основании (50) и выражения G^x,^) = Z*G^x,i^ , решение (54) может быть приведено к виду:

У ^- 9=Ё^ук (9^ ЙИ -Ё^Ж - Ё W^ -(so v=i Av ~ Л у                      Av — Л    V=1 Лу — Л а j-я координата вектора У* представлена выражением: yX^x)=Sk|e"'“y;С

V=1 где

N4w;x)=-7===^^                  1...... i •

1 V(YXv"X)

Тогда обобщенный отклик У* (х, г) системы с демпфированием на гармоническое воздействие с амплитудой F* (£,) и частотой Vx будет иметь вид:

.                    У* (х, t) = JSR* (х, £; X)F* ^<Й, • е^* = У* (х)^',(59)

О а выражение для у-й координаты вектора У* (х, /), соответственно, вид:

У* (^ 0 = У, ^е*^* = |^ (х)|«Л'"“^ .(60)

Следовательно, стационарный режим вынужденных колебаний СМС находится из уравнений (52) и (59), в которых матрица 91 (х, £; X) играет роль матрицы преобразования 5 мерного пространства алгебраических (вещественных или комплексных) амплитуд обобщённых сил при одночастошом гармоническом воздействии на механическую систему с S степенями свободы в соответствующее пространство алгебраических амплитуд обобщенных координат системы Зная свойства и характеристики элементов этой матрицы, можно сделать заключение о поведении и динамических свойствах системы в целом. Для определения основных динамических свойств, например, консервативной системы воспользуемся элементами р^ (х, £; X) матрицы 91 (х, £; X), которые в соответствии с уравнениями (49), (50) и (51) имеют вид:

• р, (х, % х)=i *-м*» ®-1^, (*. у ,          («о

v=l Л.у ~ Л        v=l ^v ~ где 8^ (х, %) - собственные податливости, которые определяются соотношением

В соответствии с тем, что 8^ (х, £) = ^ 8^ (х, 4), будем иметь

8jx^) = ^(x,§,0),                         (63)

то есть, при нулевой возмущающей частоте (А = 0) функция р^ = 8^ есть элемент матрицы Грина G(x, £). Фиксируя х и £ в каждом члене (р^ суммы (61) получаем выражение частотной гриновской функции одномассовой системы, имеющей собственное число X_v и собственную статическую податливость 8^.. Отсюда следует, что динамическая система с S степенями свободы, характеризуемая матрицей ЧГФ (см. формулы 49-51), может рассматриваться как СМС, образованная из 5 самостоятельных подсистем, имеющих одну степень свободы и соединенных последовательно. Каждая из этих подсистем имеет собственное число X_v и матрицу собственной податливости G_v (х, £) = ^8^ (х, ^)J, такие, что

9i(x,5;X) = £-^Gv(x,2;). (64)

Следовательно, методом системного анализа (MCA) можно назвать математический метод, базирующийся на свойствах и понятиях матрицы ЧГФ, а основным его уравнением считать уравнение, выражающее обобщенный комплексный закон Гука^-.

»^=£££MW7.KeM;,eN, (65) ^=l J=15=1 ■ где МА^ - алгебраическая (комплексная или действительная) амплитуда стационарных вынужденных колебаний (СВК) к-й точки .м-го структурного элемента СМС по обобщенному направлению & возбуждаемых у-ми обобщёнными силовыми функциями Fp, имеющими различные фазы, различные обобщенные направления ц, но общую круговую частоту to; f 91^ (^) - частотная гриновская функция какой-либо М-й подсистемы, или М-го структурного элемента (абсолютно твердого, упругого или упруго-жидкого) СМС. При этом нижний индекс М указывает номер тела, или подсистемы (структурного элемента) СМС, которому принадлежит точка К, а верхний индекс N - номер тела (подсистемы), структурного элемента СМС, которому принадлежит J-я точка. Таким образом, основное уравнение MCA позволяет определить амплитуду стационарных вынужденных колебаний в произвольной точке любой СМС через известные ЧГФ, амплитуды и фазы силовых факторов, имеющих общую круговую частоту со.

Применив к , А; Эрмитово разложение и выражая модуль _MA^=^Re _МА^² +^Jm_M^² и аргумент _яа^ =arctg^Jm₃₍^/Reчерез действительную и мнимую части числа _м^, находим закон СВК к-й точки системы по с обобщенному направлению

^лАЧ^о^'+Х)-

Так, например, для системы (6), на r-й вход который подается воздействие вида F_r(f) = F_Or cos tot, а демпфирование учитывается по гипотезе вязкого трения, закон СВК будет иметь вид, полностью совпадающий с результатом (28), полученным методом главных координат.

Шепоеалое Е.Н. Некоторые алгебраические аспекты метода системного анализа в общей теории сложных механических систем

Таким образом, задача отыскания динамического отклика системы на внешнее воздействие свелась к нахождению ЧГФ, что представляет собой, в большинстве практических случаях, сложную вычислительную проблему. Однако, анализируя изложенный выше материал приходим к выводу, что элементы ^(х^Х) матрицы ЧГФ й^(Х)есть динамические податливости (ДП) структурных элементов системы, то естьМ^С^^^С^)- Следовательно, MCA - математический метод, базирующийся на свойствах и понятиях матрицы ЧГФ (ДП), а основным его уравнением является уравнение^-.

^м Sy nj - tM Sy л/

ЛW = LLL w №Л К G М;; е N. (66) JV»1 J—\ Tj=l N=1 J=1 т]»1

Но введение основного уравнения MCA еще не упрощает решение задачи о колебаниях СМС, особенно при большом числе S, а в ряде случаях, например, синтезе и т.п. оказывается практически бесполезным. Более эффективным средством исследования СМС является выражение ЧГФ (ДКП) через ЧГФ (ДКП) изолированных подсистем, что позволяет сократить число необходимых операций в вычислениях [18]. Рассмотрим одно из таких средств. Операторная матрица Т>(ю) СМС представляется как крупноблочная матрица D, каждый диагональный блок которой Dp, называемый ниже в тексте свободной диагональю, содержит в себе информацию о поведении изолированных подсистем, а информация о взаимодействии (связях) между подсистемами, образующими в целом СМС, содержится в ее недиагональных блоках. При установлении связей между отдельными подсистемами элементы матрицы D изменяются. Измененная матрица D представляется выражением

'D='D-R, (67) в котором элементы матрицы D являются собственными операторами СМС, а элементы матрицы R - операторами взаимодействия. Если известна обратная матрица Т для функции D, то обратная функция для Т>ф'^х = Р) может быть получена по формуле

'Р = 'Р(Е-КРух.

Таким образом, для определения выражения ЧГФ (ДКФ) исходной СМС через ЧГФ (ДКФ) изолированных подсистем все связи устраняются. Сложная механическая система приводится к совокупности изолированных подсистем. Восстановив часть связей и применив формулы (66) и (68), выражаются ЧГФ (ДКФ) промежуточной системы через ЧГФ (ДКП) изолированных подсистем. Восстановив все связи, получаем искомое выражение для ЧГФ (ДКП) всей СМС.

Рассмотрим для примера якобиевую (цепную) СМС Л, с описывающим оператором Д, вида:

	б б	«1 б Х2	б «2 б	... б ... б ... б	б б б	б б б
As” Д, + Ад ~ Д , +			•	•е •		•
	б	б	б	... б	42	б
	б	б	б	Xs-2	б	41
	б	б	б	... б	Xs-1	б

где А3 - оператор канала самодействия диагональной Ар системы; б - SxS матрица нулевых операторов; Ар - описывающий оператор свободной диагональной системы ( Ар =GT - гриновский оператор); (к?хР - операторные образующие каналов взаимодействия; б - нулевые опе раторы.

Анализ матричной структуры описывающего оператора Д. (69) показывает, что якобиевая система А, представляет собой совокупность S взаимодействующих подсистем, в которой любая из подсистем Ду(1< j

Один из алгоритмов построения S - представления гриновского оператора б^якобиевой системы (69) может быть представлен в виде:

д3=^х^+х^к з-хх^к хх^к-Лдр,^g3 =дР1(£°у1(1^г1+Д)"1(]^^                    i0^)1^)"1 к где (Х,К),(Х°,К°) - операторные SxS матрицы образующих каналов самодействия возмущенной диагональной Ар системы; первые из них определены на линейном пространстве Е = GD Т, вторые - на линейном пространстве Т допустимых входов; Xk,Kk(X^K^) - операторные SxS нижние (верхние) треугольные матрицы; 5 - операторная SxS единичная матрица; GP - гриновский оператор диагональной системы Ар.

Анализ вышеизложенного показывает, что в своей математической основе MCA базируется на изучении динамики свободных и некоторых фиктивных систем. Является достаточно общим, описывающим динамические свойства СМС различной природы, не требующим составление дифференциальных уравнений. Его эффективность особенно ярко проявляется при исследовании СМС содержащих в своем составе хотя бы одну континуальную подсистему, а также в задачах, в которых исследуют изменение свойств и структуры системы или изменении только некоторых ее параметров, поскольку метод позволяет при каждом изменении структуры системы или каких-либо ее параметров повторять сравнительно небольшую часть полного расчёта, который требуется при использовании традиционных методов [16]. В ряде случаев этот метод оказывается изоморфным таким известным методам, как методу факторизованных возмущений; исследования сложных систем по частям; сечений; парциальных откликов; динамических жесткостей (податливостей); части некоторых матричных методов: начальных параметров, методу прогонки; МКЭ, а также методу (с аналогичным названием), который получил применение в США при динамическом анализе и испытаниях космических комплексов, представляемых в виде СМС, состоящих из подсистем: космического аппарата; носителя; пусковой установки [17].