Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

спользование многокомпонентных материалов, широко применяемых в настоящее время в строительстве, порождает известные технологические трудности, связанные как с зависимостью структуры и свойств композита от содержания компонентов, так и с погрешностью при дозировании компонентов (последнее проявляется наиболее ярко при использовании наноразмерных объектов, вводимых в микроколичествах). Предположим, что допустимое варьирование содержания компонента, не вызывающее существенного изменения свойств, составляет ∆ q_i ( i = l,n, n – количество компонентов), а погрешность дозирования – δ q_i . Допустимо принять, что ошибки дозирования подчинены нормальному распределению. Тогда вероятность введения компонента в количестве, не выходящем за границы варьирования, равна

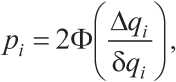
где ФИ=

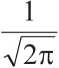
t

X

I exp-- ax – функция Лапласа.

О к 2 7

Если погрешности дозирования независимы, то вероятность получения материала заданного состава равна

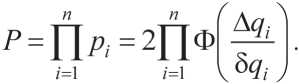
Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

Таблица 1

Зависимость вероятности (2) от соотношения ∆ q_i / δ q_i и состава материала

Количество компонентов	Соотношение ∆ qi / δ qi
	0,5	1	2	3	4	5
3	0,056	0,318	0,869	0,992	0,999	1,0
4	0,022	0,217	0,830	0,989	0,999	1,0
5	0,008	0,148	0,792	0,986	0,999	1,0
10	6,78·10–5	0,022	0,628	0,973	0,999	1,0

При ∆ q_i / δ q_i > 4 вероятность (2), выражающая устойчивость технологического процесса к случайному варьированию рецептурных факторов, близка к единице (табл. 1).

При ∆ q_i / δ q_i < 3 состав материала оказывает существенное влияние на устойчивость технологического процесса к случайному варьированию рецептурных факторов, особенно при использовании оборудования, не позволяющего производить дозирование малых количеств компонентов ( ∆ q_i / δ q_i < 1). Кроме того, полученные данные показывают, что затруднительно получить качественное изделие из материала, для которого имеется сильная зависимость свойств от рецептуры (рис. 1).

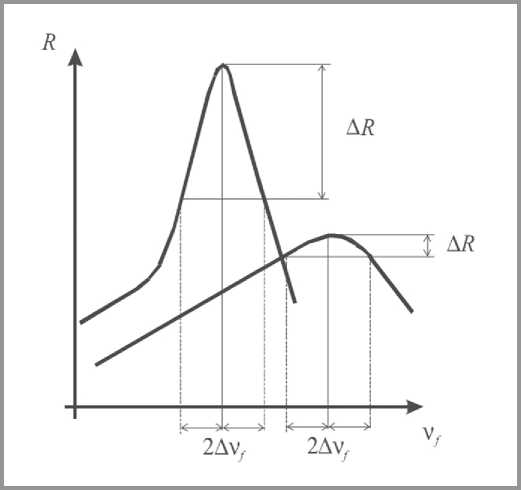
Рис. 1. Зависимость прочности от содержания дисперсной фазы

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

Очевидно, что указанные трудности возникают в многофазных материалах. В данном случае под фазой понимается однородная по химическому составу и физическим свойствам часть термодинамической системы, отделенная от других частей (фаз), имеющих иные свойства, границами раздела, на которых происходит изменение свойств [1]. В соответствии с правилом фаз Гиббса, число фаз, сосуществующих в равновесии, не превосходит числа независимых компонентов более чем на два [2]:

C = K + N – F , (3)

где С – вариантность системы; К – количество компонентов; F – количество фаз; N – количество независимых переменных (принимается N = 2 – давление и температура).

Это означает, что при равенстве К и F система дивариантна, т.е. можно, не нарушая равновесия, изменять только два параметра (например, концентрацию двух компонентов или концентрацию одного компонента и температуру). В этом случае возможности технолога по организации технологического процесса производства, устойчивого к случайному варьированию рецептуры, существенно ограничены. При необходимости варьирования только концентрациями компонентов максимальное количество фаз F_max = 3, а при необходимости изменения концентраций компонентов и одного независимого параметра – F_max = 2, при изменении всех переменных системы (рецептуры, давления и температуры) – F_max = 1.

Таким образом, подбор компонентов многокомпонентного материала должен обеспечивать формирование фаз, число которых значительно меньше числа компонентов ( F <  K ). На практике указанное может быть реализовано посредством использования агрегатив-но- и седиментационно-устойчивых систем – лиофильных коллоидных растворов – и зерновых смесей, содержащих не более двух фракций с соотношением диаметров зерен D/d > 8 [3].

В работах В.И. Калашникова посредством наработки и обобщения существенного объема эмпирических данных предложено решение, обеспечивающее повышение показателей эксплуатационных свойств многокомпонентных композитов [4–10]. Сущность предложенного решения заключается в формировании оптимальной топологической структуры многокомпонентного материала путем оптимизации разме-

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов ров зерен дисперсной фазы определенной химической природы совместно с гиперпластификаторами.

Эмпирические данные, полученные В.И. Калашниковым, могут быть положены в основу методики проектирования составов композиционных материалов с повышенным содержанием дисперсной фазы. Количество дисперсной фазы определяет технологические свойства смеси (подвижность, удобоукладываемость) и эксплуатационные свойства композита. При этом возникает типичная оптимизационная задача, ограничениями в которой являются: получение высокоподвижной смеси ( τ → τ _min при ν → ν _{f ,min}, где ν _f – объемное содержание дисперсной фазы) и максимальных величин показателей эксплуатационных свойств ( F_j → F_{j ,max} при ν→ ν _{f ,max}). В общем случае топологическая модель содержания дисперсной фазы может быть представлена в «двухструктурном» виде (рис. 2), причем ν _{f ,min} = 0,52 (структура I), ν _{f ,max} = 0,74 (структура II). Компромисс достигается при равном содержании каждой «структуры». В этом случае объемная доля дисперсной фазы будет равна ν _f = 0,63, а дисперсионной среды – ν _m = 0,37. Полученные результаты можно использовать для определения числа структурных уровней (и фаз) композита. Имеем:

( ν m ) ^k = ν I ,                                                                      (4)

где ν _I – первый порог перколяции ( ν _I = 0,16) [11]; k – количество структурных уровней.

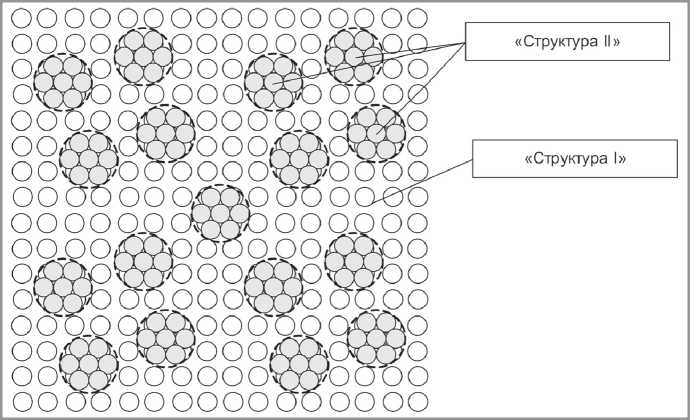
Рис. 2. «Двухструктурная модель» композита

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

Из (4) следует:

k = log _{ν m} ν _I ≈ 1,84 ∼ 2, (5)

что соответствует положениям полиструктурной теории В.И. Со-ломатова [12], согласно которой проектирование композиционных материалов достаточно (с инженерной точки зрения) проводить на двух масштабных уровнях: микро- и макроструктуры. При этом в качестве критерия оптимизации на микроуровне целесообразно выбрать подвижность смеси, а на макроуровне – прочность композита.

Требование по обеспечению максимального содержания дисперсной фазы на двух масштабных уровнях предопределяет реализацию схемы проектирования состава материала, представленную на рис. 3; индексы « m » и « f » соответствуют матричному материалу (дисперсионной среде) и дисперсной фазе.

Результаты расчета объемных долей компонентов, произведенного по предлагаемой схеме, приведены в табл. 2.

Взаимодействие воды с фильной твердой поверхностью приводит к формированию на границе раздела фаз плотного слоя воды, физические свойства (вязкость, плотность, температура замерзания и др.) которой существенно отличаются от аналогичных показателей для воды в объеме. Адсорбция воды и изменение ее свойств в тонких слоях будут оказывать влияние на объемное распределение фаз в композите. Прове-

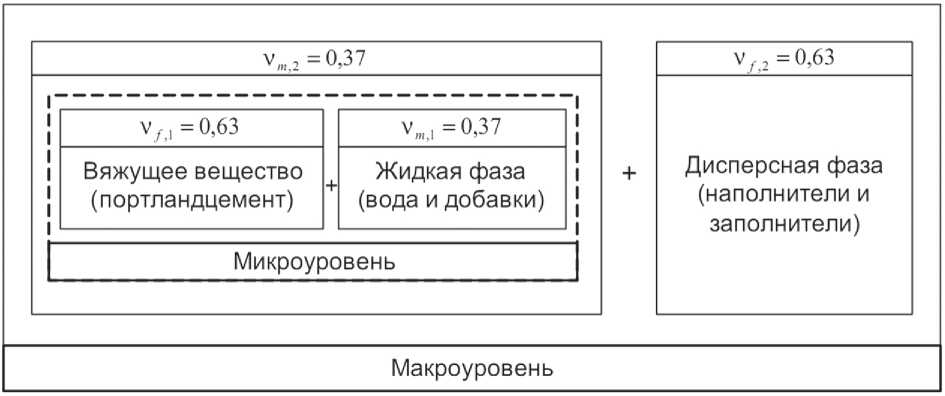
Рис. 3. Схема проектирования состава композита

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

Таблица 2

Результаты расчета состава бетона в соответствии со схемой на рис. 3

Наименование компонента Объемные доли Расход компонентов, кг/м3 итерация №1 итерация №2 итерация №3 по предлагаемой схеме по данным [10] Вяжущее вещество (портландцемент) 0,233 0,233 0,233 723 720 Жидкая фаза (вода с добавками) 0,137 0,219 0,219 219 220 Дисперсная фаза: – диаметр зерен D – диаметр зерен dm – диаметр зерен d 0,630 0,548 0,548 1453 1482 0,386 1024 1050 0,143 378 360 0,019 51 72 дем расчет изменения объема композита при наличии граничного взаимодействия. Запишем уравнение плотности композита

Р = РЛ + РЛ> V^+Vy =1,                              (6)

где ν _i и ρ _i – объемная доля и плотность компонента.

Изменение объема композита будут равны м w = v vo,vo = z + m,                                   (7)

Р/ Pm где Мi – массы компонентов.

С учетом образования пленочной фазы запишем объем композита равным:

V = 7/ + Vp + yt где индексами «р» и «t» обозначены соответственно объемная и пленочная фазы дисперсионной среды.

Объем пленочной и объемной фазы:

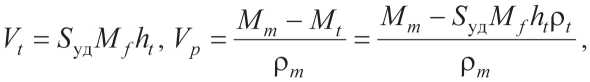
где h_t – толщина пленочной фазы; ρ _t – плотность пленочной фазы; S_уд – удельная поверхности дисперсной фазы.

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

С учетом V_t и V_p объем композита равен

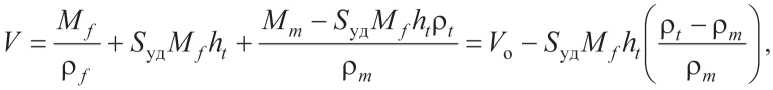
а изменение объема

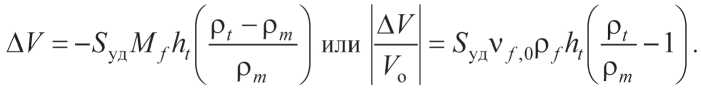
При этом изменение объемной доли дисперсной фазы будет равно:

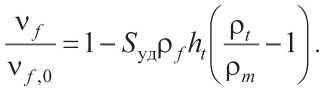
Экспериментальное определение величин S_уд , h_t и ρ _t сопряжено с определенными трудностями, поэтому в научно-технической литературе существуют различные сведения по указанным величинам даже для хорошо изученного вещества – воды. Например, в [13] на основе трехслойной модели показано, что толщина квазикристаллической воды составляет h_b ≥ 30 нм, а в работе [14] – до 10 нм. Другой важной особенностью, влияющей на реологические свойства (подвижность) смеси, является обтекание жидкостью частиц дисперсной фазы. При этом формируется пограничный слой, толщина которого пропорциональна [15]:

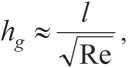
где Re – число Рейнольдса; l – характерный размер тела.

Плотность связанной воды зависит от степени гидрофильности по- верхности твердого тела и варьируется в очень широком диапазоне значений – от 0,73 до 3,02 г/см3 [14]. Такие же сложности возникают при определении удельной поверхности дисперсной фазы, особенно при учете ее шероховатости [16].

Для оценочных расчетов изменения ν _f можно использовать упрощенную формулу

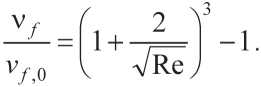
При граничном значении числа Рейнольдса (режим, соответствующий работе современных быстроходных смесителей) отношение

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

ν _f/ ν _f,0 = 0,13. Расчеты, проведенные по данным В.И. Калашникова, дают близкие значения ν _f/ ν _f,0 = 0,112 [10].

С учетом указанного, объем дисперсной фазы уменьшается, жидкой фазы – увеличивается (итерация № 2, табл. 2).

Для определения количества каждой фракции дисперсной фазы можно использовать модель, представленную на рис. 4.

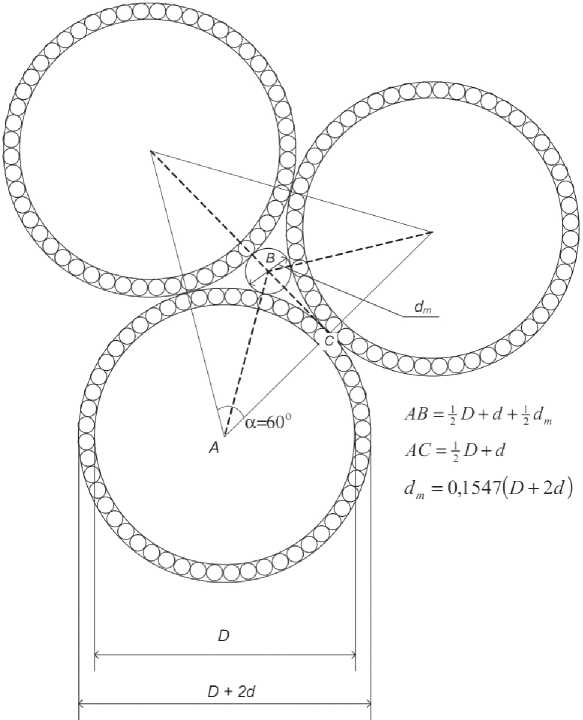
Рис. 4. Модель для расчета дисперсной фазы

Количество фракции дисперсной фазы с диаметром частиц D равно:

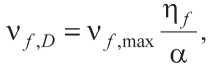
где ν _{f, max} – максимальное количество дисперсной фазы ( ν _{f, max} = 0,548,

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов табл. 2); ηf – максимальная степень наполнения монодисперсными сферами (ηf = 0,74); α – коэффициент раздвижки зерен, равный [3]

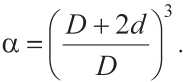
При заданном значении α можно вычислить значение соотношения D/d :

D _   2

d Vot-1

Количество фракции с диаметром частиц d определяется из соотношения:

t/^l-rijv^

а с диаметром d_m – из соотношения:

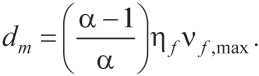
Результаты расчета, произведенного по соотношениям (14)...(19), также представлены в табл. 2 (итерация № 3, α = 1,05). Анализ табл. 2 (для итерации № 3) показывает, что количества фракций с размерами частиц d и d_m меньше величины ν _I . Преодоление указанного возможно посредством подбора дисперсной фазы, размер частиц которой не будет превышать диаметра частиц цемента. Расчет соотношения D/d показывает, что оно изменяется в широких пределах: при α ∈ [1,05; 1,10] соотношение D/d ∈ [60; 120].

Состав, спроектированный по предлагаемой методике, а также состав высокопрочного бетона, подобранный эмпирически [10], приведены в табл. 2. Сопоставление расходов компонентов указывает на хорошую сходимость результатов проектирования состава по предлагаемой методике. Особенно – при учете существенного отличия габитуса зерен дисперсной фазы от сферической формы, так как известно, что число Ньютона для фигур неправильной формы (12 <  K_N < 26) [17] больше K_N для сфер ( K_N = 12).

Е.В. КОРОЛЕВ и др. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов

Уважаемые коллеги!

При использовании материала данной статьи просим делать библиографическую ссылку на неё:

Королев Е.В., Смирнов В.А., Альбакасов А.И. Некоторые аспекты проектирования составов многокомпонентных композиционных материалов // Нанотехнологии в строительстве: научный Интернет-журнал. М.: ЦНТ «НаноСтроительство». 2011, Том 3, № 6. C. 32–43. URL: (дата обращения: _________ _____).

Dear colleagues!

The reference to this paper has the following citation format:

Korolev E.V, Smirnov V.A., Albakasov A.I. Some aspects of mixture design for multicomponent composites. Nanotechnologies in Construction: A Scientific Internet-Journal, Moscow, CNT «NanoStroitelstvo». 2011, Vol. 3, no. 6, pp. 32–43. Available at: magazine/nb/ (Accessed _____________). (In Russian).