Некоторые автомодельные закономерности развития поврежденности при квазихрупком разрушении твёрдых тел

феноменологических моделей, использующих эмпирическую информацию о поведении материала при различных историях нагружения [1].

В работах Л.М. Качанова и Ю.Н. Работнова [2, 3] для описания процесса накопления повреждений впервые вводится скалярный параметр поврежденности, определяемый площадью трещин, приходящихся на единицу площади поперечного сечения тела. Дальнейшим развитием данного подхода стал учёт анизотропии процесса накопления повреждений и введение тензорных параметров поврежденности [4–7], в общем случае не связанных с какой-либо характеристикой реальных дефектов материала.

В работах [8, 9] в рамках статистической модели твердого тела с мезоскопическими дефектами вводится тензорный параметр поврежденности материала, который имеет смысл параметра порядка среды, а именно деформации p , обусловленной появлением дефектов:

Pk = nW . (1)

Здесь n — плотность микродефектов, s k — тензор, описывающий геометрию sk = 2 s (v bk+bvk)

единичного микродефекта, компоненты которого имеют вид:

для микросдвига (vi — компоненты единичного вектора нормали к плоскости сдвига v ; bk — компоненты единичного вектора направления сдвига b ; s — интенсивность сдвига) и s ik = svivk для микротрещины (vi — компоненты единичного вектора нормали к основанию микротрещины, s — объем микротрещины). Анализ результатов решения статистической задачи поведения ансамбля дефектов под действием внешнего силового поля для различных типов дефектов позволил установить существование второго параметра порядка среды с мезодефектами — параметра структурного скейлинга 5, связанного с двумя характерными масштабами: размером зародышей дефектов и расстоянием между дефектами [8].

В работе [8] методами неравновесной термодинамики для введенных параметров порядка получены кинематические соотношения статистической модели. В одномерном случае (когда p xx = p , p xy = p yy = p_zz = 0) они имеют вид

дp      дF д ( дp

— = — Г 1 1 к — д t     p дp дx \ дx

д5-_Г _ дt " 8 д5,

где Г_p , Г ₅ — кинетические коэффициенты, K — коэффициент, описывающий эффекты нелокальности в ансамбле дефектов, F — свободная энергия среды с мезодефектами.

Кинетические уравнения (2) определяют характерные реакции материала на приложенное напряжение о : субмикрокристаллическое ( 5 >5 * ) , пластическое ( 5 c <5 <5 * ) или квазихрупкое ( 5 <5 c ) поведение (Рис. 1) [10]. Под термином «субмикрокристаллическое» понимается особое деформационное поведение материала, наблюдающиеся для поликристаллов с характерным размером зерна порядка 100 нанометров. Автомодельный характер развития поврежденности при квазихрупком разрушении материала впервые был исследован в [8]. Как развитие этих результатов в настоящей работе проводится детальный качественный анализ автомодельных решений.

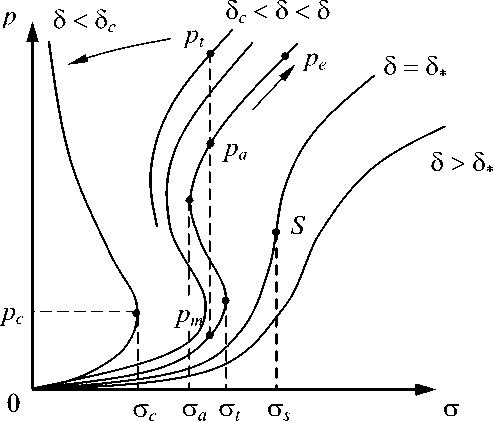
Рис. 1. Характерные нелинейные реакции среды на рост локализованных сдвигов в зависимости от напряжения о для различных значений параметра структурного скейлинга 5

Следуя [8, 9, 11], в окрестности критической точки ( о c , p c ) (Рис. 1) кинетическое уравнение для параметра поврежденности (2) можно записать в виде квазилинейного параболического уравнения:

d p - e _s4 р , о c ) +# q . ² ( p P ] , Ot               Оx V        оx )

где о c — приложенное критическое напряжение; Q^ ( р , о c ) , Q _а ² ( р ) — полиномы степени в и а соответственно (степень полинома определяется принятыми аппроксимациями сводной энергии и коэффициента нелокальности).

При достаточно больших значениях p в уравнении (3) можно пренебречь влиянием напряжения и учесть только старшие степени полиномов Q^ ( р ) , Q _a ² ( р ) . Тогда уравнение (3) можно записать в виде:

5 р в ,5 f ар ) — = qp +—I кр —I , а t аx V аx )

где q и к — коэффициенты при старших слагаемых Q^ ( р ) , Q _a ² ( р ) .

Применительно к задачам газовой динамики, термодинамики, магнитной гидродинамики и нелинейной диффузии, как показано в работах в [11–13], в системе, эволюция которой описывается соотношением типа (4), могут существовать три типа автомодельных решений (три характерных режима) с обострением. Особенностью этих режимов является асимптотическое обращение рассматриваемой переменной в бесконечность за конечный промежуток времени. Реализация каждого из режимов зависит от величины параметров а и в •

HS-режим . При 1 < в < а + 1 в рассматриваемой среде реализуется волновой режим развития начального возмущения; за конечное время поврежденность возрастает до бесконечности во всем рассматриваемом пространстве.

S-режим. При в = а +1 увеличение плотности дефектов до бесконечности за конечное время происходит в локальной области рассматриваемого пространства, называемой фундаментальной длиной Lf . В этом режиме решение единственно и может быть получено в аналитическом виде p (x, t) = ( q (t - tc))1 а

2 (а +1)

sin

а(а + 2)

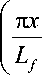
где L f = 2 — VO+ 1 Jк/ q и имеет смысл пространственного периода решения, а

2 ( а + 1 ) 1 не зависящего от начального распределения поврежденности p ; t c =—)-------- —

а(а + 2) pаq время обострения ( p0 — максимальное значение p в области начального возмущения). Время появления очага разрушения тc складывается из двух времен: собственно времени обострения tc (времени обострения автомодельного профиля) и времени индукции tu (времени, необходимого на формирование автомодельного профиля при данном уровне нагрузки).

LS-режим . При а + 1 < в < а + 3 решение неединственно, так как в среде образуется конечное число диссипативных структур обострения (в отличие от HS- и S-режимов, при которых образующиеся структуры имеют единственную структурно устойчивую пространственно-временную форму). Спектр пространственно-временных форм диссипативных структур определяется из решения задачи (4) на собственные функции и собственные значения. Появление сложных диссипативных структур (структур, соответствующих старшим собственным функциям задачи (4)), формирующихся из простых, происходит только при достаточной близости к автомодельному решению начального профиля деформации, обусловленной дефектами. Образующиеся структуры имеют различный масштаб локализации, который зависит от свойств среды и максимального значения начального профиля. Численный анализ показывает, что объединение простых структур в сложные происходит при расстояниях между простыми структурами L_c , близких по величине к L_f .

Особенностью LS-режима является зависимость фундаментальной длины и времени обострения от профиля начального возмущения. Выражение для L_f получено в [12] из мажорантных соображений:

Lf =

2 (а +1 + р) к \ а(Р- 1)q

nV ( а+3-в )

W o^

Здесь W₀ = ap max , где a — размер области начального возбуждения, p _max — максимальная плотность дефектов в этой области. В случае a >  L f выражение (5) имеет вид:

L f =^п

2 (а+ 1 + в) k (а+1-в)/2 p0        , где p0 — максимальное значение плотности дефектов вблизи центра симметрии начального профиля. Время обострения в LS-режиме может быть оценено сверху как t2

(а + 1 + Р)Да + 2)^р-Щ p ^{e— 1} ( t 1 ,0) q

где p ( t 1 ,0) — максимальное значение плотности дефектов вблизи центра симметрии в момент t ₁ , когда начальное возмущение выходит на автомодельный профиль. Стоит отметить, что в LS-режиме процесс обострения локализуется в пространственной области, которая со временем уменьшается.

Решение, соответствующее НS-режиму, активно применяется при моделировании задач горения, взрыва, физики плазмы и эволюции биологических систем [13]. Решения, отвечающие S- и LS-режимам, использовались, в частности, при построении модели ветвления трещин в квазихрупких материалах и при моделировании процессов ветвления трещин и распространения волн разрушения [14, 15].

В рамках рассматриваемого статистического подхода актуальной задачей является установление возможного типа автомодельного решения с обострением для кинетического уравнения, определяющего развитие поврежденности в случае квазихрупкого поведения материала для произвольного начального уровня повреждённости и значения приложенного напряжения.

Описание развития дефектной подсистемы при формировании очага макроскопического разрушения как автомодельного решения в режиме с обострением является качественно новым результатом в физике и механике разрушения. Аналогичные предположения о появлении обостряющихся локализованных структур при разрушении обсуждались ранее в работах [16–20]. Наличие нелинейности и объемных источников в эволюционном уравнении для параметра поврежденности является принципиально важным моментом для нагруженного твердого тела как открытой самоорганизующейся системы [21].

• 2.    Качественный анализ кинетического уравнения для параметра поврежденности

Для установления возможных сценариев развития локализованной поврежденности в квазихрупком материале при фиксированном напряжении проведем качественный анализ кинетического уравнения (2) с использованием метода усреднения, предложенного в работе [22]. Этот метод широко применяется для анализа нелинейных параболических дифференциальных уравнений, возникающих в различных областях науки [23, 24].

Рассмотрим симметричную область с ненулевой поврежденностью p , локализованную в одномерном пространстве. Для описания квазихрупкого поведения материала аппроксимируем неравновесную свободную энергию полиномом десятой степени. Такой вид аппроксимация является прямым следствием решения статистической задачи эволюции дефектов в квазихрупком материале [10]; при этом уравнение эволюции поврежденности преобразуется к виду:

a p    эГа p )

=1 KI — Г д t дx v дx )    р

152,3810 ст    <          1,2381 )            ₂

0,0457--,------ + p 5,8528 —,---- — 11,8924 p ² +

5          I             I

+ 16,7908 р ³ - 15,0209 p ⁴ + 8,6888 p ⁵ - 3,2777 p ⁶ + 0,7996 p ⁷ - 0,1215 p ⁸ +           (8)

+ 0,001 p ⁹ - 0,0003 p ¹⁰

В последующих выкладках в уравнении (8) примем Г р = 1, что не нарушает общность задачи. Для оценки влияния нелинейности на кинетику локализованной структуры рассмотрим два случая значений коэффициента нелокальности: постоянный K = K ₀ и нелинейный K = K ₀ е^р .

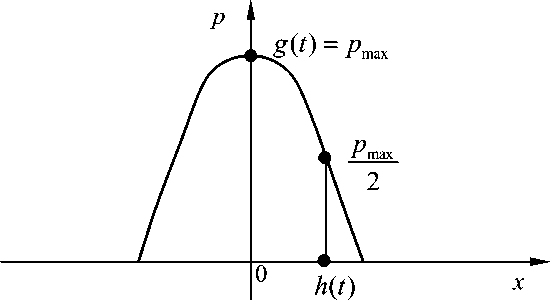
Рис. 2. Локализованная диссипативная структура параметра плотности дефектов

Согласно [22] предположим, что решение уравнения (8) представимо в виде

P (x, t ) = g (t) f (У, ^ = xh (t), где функция g (t) описывает эволюцию амплитуды структуры с течением времени, h (t) — эволюцию координаты полуширины с течением времени, f (^) — пространственную форму структуры (Рис. 2). Далее, интегрируя (8) по пространственной переменной и полагая, что на бесконечности поток w (t, x ) = KTx обращается в нуль, получим следующее уравнение:

7 TO                           TO 77-r ddF — p (t, x) dx = - ---dx. dt                dp

-TO                    -TO r

Умножая (8) на p ( x , t ) и интегрируя по пространственной переменной, найдем:

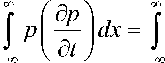
p dx

K

I

f dp 1^ Idx Jv

P ⁵ ^ л dx - ---- dx.

-TO ^d P

Подставляя представление (9) в (10) и (11), придем к системе обыкновенных дифференциальных уравнений относительно временных производных амплитуды диссипативной структуры и координаты полуширины при постоянном коэффициенте нелокальности:

g _ ^gK 0 A 1 + B | ₀,₀467 -

+ 11,8924 g ² ( A ₂ - B ₂ ) -

h ^{2         1} к

152,3810 g 5

- 16,7908 g ³ ( A3 - B3 ) + 15,0209 g ⁴ ( A ₄ - B ₄ ) - 8,6888 g ⁵ ( A5 - B₅ ) +

+ 3.2776 g ⁶ ( A - B ₆ ) - 0,7886 g ⁷ ( A ₇ - B ₇ ) + 0,1215 g ⁸ ( A - B 8 ) -

<

- 0.0104 g ⁹ ( A - B ₉ ) + 0.0003 g ¹⁰ ( A ₁₀ - B ₁₀ ) ,

h = - KA h

-B1h| 0,0467- 152,3810g | + h| 5,8528- g к             5 J к

1,2381 A

5 J

-11,8924 gh (2A2 - B2) +16,7908g2 h (2A3 - B3)-15,0209g3 h (2 A4 - B4) + +8,6888g4 h (2A5 - B5)- 3,2776g5 h (2A6 - B6) + 0,7886 g6 h (2A7 - B7 ) --0,1215g7 h (2 A - B8) + 0,0104g8 h (2 A - B9)- 0,0003g9h (2 A10 - B10), где A =J- fnd ^ • B   _IfdA;  A J- fd ^ -  B _ f- fd ^

П, П ^1                                 n, n ^1                                     11

,     L fd ^      ,     L f ² d ^       L f ² d ^       L f ² d ^

при переменном коэффициенте нелокальности g = ^LL + SKA + b!0,0468 -152-3810g 1 +11,8924 g 2 (A 2 - B2)-h h к5 J

- 16,7908 g ³ ( A ₃ - B ₃ ) + 15,0209 g ⁴ ( A ₄ - B ₄ ) - 8,6888 g ⁵ ( A ₅ - B ₅ ) +

+ 3,2777 g ⁶ ( A 6 - B 6 ) - 0,7886 g ⁷ ( A 7 - B 7 ) + 0,1215 g ⁸ ( A - B 8 ) -

- 0,0104 g ⁹ ( A - B 9 ) + 0,0004 g ¹⁰ ( A_to - B _w) ,

h _ -g K0L -KA-BAf0,0468- 152,3810g) + h(5,8528- 1,2381)-h h g к             5 J к 5 J

- 11,8924 g h ( 2 A ₂ - B ₂ ) + 16,7908 g ² h ( 2 A ₃ - B ₃ ) - 15,0209 g ³ h ( 2 A ₄ - B ₄ ) +

+ 8,6888 g ⁴ h ( 2 A5 - B ₅ ) - 3,2777 g ⁵ h ( 2 A ₆ - B ₆ ) + 0,7886 g ⁶ h ( 2 A ₇ - B ₇ ) -

- 0,1215 g ⁷ h ( 2 A 8 - B ₈ ) + 0,0104 g ⁸ h ( 2 A 9 - B ₉ ) - 0,0004 g ⁹ h ( 2 A₁₀ - B ₁₀ ) ,

,^- n             p   n +1           p  , 2            p            p pp, 2 _

-—j        в      j-—a    -—7        в    j-—l   j-—/ roo riv ;   n^n,n^1      j-oo p7 IV ;   ^ j-oo p7 IV ;   "L,1     ЛОО p7 IV ;   ^4        roo p.7 4v

f  fd ^      , f f2 d ^ f  f2 d ^        f  f2 d ^         f  f2 d ^

Рассмотрим условия равновесия одиночной локализованной структуры с начальной амплитудой g (0) _ g0 и полушириной h (0) _ h0. Форма структуры описывается уравнением y _ a (x + b)2 + c, где константы a, b, c являются решениями системы уравнений ab2 + c _ g0,

a ( - h 0 + b ) + c _ p° , a ( h ₀ + b ) 2 + c _ g2-.

На рисунке 3 представлены положения равновесия одиночной симметричной локализованной структуры для различных уровней напряжения при 5 = 0,8 и K0 = 1. Из анализа кривых видно, что одному напряжению соответствуют две равновесных амплитуды структуры с различными размерами. Вид коэффициента нелокальности влияет на характер кривой соответствия равновесной амплитуды и полуширины.

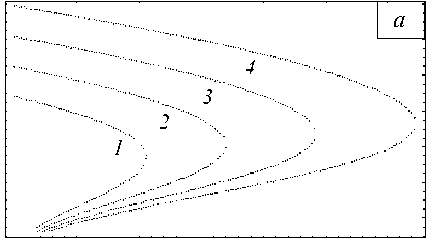
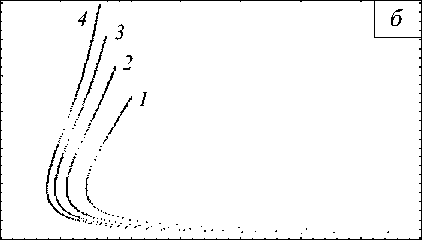
Характерные равновесные диаграммы для различных значений параметра структурного скейлинга представлены на рисунке 4. Величина кинетического коэффициента в уравнении (8), подобно коэффициенту нелокальности, определяет только равновесный размер структуры (Рис. 5).

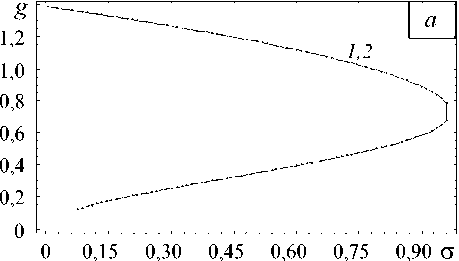
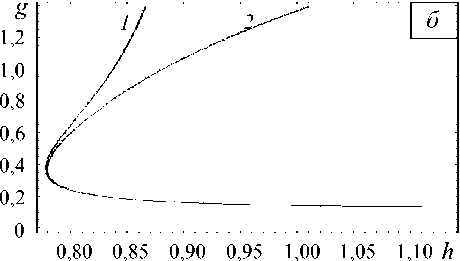
Рис. 3. Зависимость амплитуды структуры от приложенного напряжения ( а ); кривая соответствия амплитуды координате полуширины ( б ) для случая постоянного (кривая 1 ) и переменного ( 2 ) коэффициента нелокальности

g

1,4

1,2

1,0

0,8

0,6

0,4

0,2

0    0,15   0,30   0,45   0,60   0,75   0,90 а

Рис. 4. Равновесные кривые а ~ p ( а ), h ~ p ( б) для различных значений параметра структурного скейлинга 5 : 0,5 (кривая 1 ); 0,6 ( 2 ); 0,7 ( 3 ); 0,8 ( 4 )

g

1,4

1,2

1,0

0,8

0,6

0,4

0,2

0,80 0,85 0,90 0,95 1,00 1,05 1,10 h

Для исследования поведения системы в окрестности точек равновесия построим систему уравнений первого приближения для переменных u = g - g * , w = h - h * , где ( g * , h *) — положение равновесия системы при фиксированном напряжении а * (для случая нелинейного коэффициента нелокальности рассуждение и результаты аналогичны). Тогда систему (12) можно представить в виде:

du dt

dw „ dt

a11u + a12 w + F1 (u, w), a 21 u + a 22 w + F2( u, w),

g

1,4

1,2

1,0

0,8

0,6

0,4

0,2 0

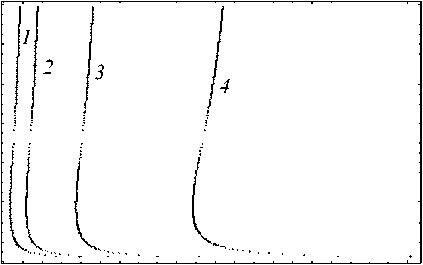
Рис. 5. Равновесная кривая h ∼ p для различных значений K ₀ Г_р : 0,1 (кривая 1 ); 0,2 ( 2 ); 1,0 ( 3 ); 10 ( 4 ).

0,50      1,00      1,50      2,00 h

где F1 (u, w), F2 (u, w) — бесконечно малые величины при (u, w) ^ (0,0), au =- 0,1 *69 -32,6192g*2 + 70,3615g*4 -81,5678g*6 + 56,6637g*8 -24,5885g40 + g*2

+ 6,713 8 g ⁴² - 1,1205 g ⁴⁴ + 0,1044 g ⁴⁶ + ²⁵ + h

476,1910 a *

*2         , g2

a ¹²       h*⁵ ’

a 21 = ^0,23 3₃ ⁸⁶⁷ + 2,7183 g*h* - 10,2344 g*³h * + 14,9818 g*⁵h* - 11,8512 g*²h * + 5,5883 g*⁹h* - g ³

- 1,6167 g⁴¹ h * + 0,2815 g⁴³h* - 0,0271 g⁴⁵h* - ^476,1 91₃ ⁰ h *°* ,

g *3

a ₂₂ = 4,3052 - ^0,1 * ₂ ⁷⁰ + 1,3591 g *² - 2,5586 g *⁴ + 2,4970 g *⁶ - 1,4814 g *⁸ + 0,5583 g ⁴⁰ - g *2

- 0,1347 g ⁴² + 7,5 + h ⁴

238,0950 a *

*2          .

g ²

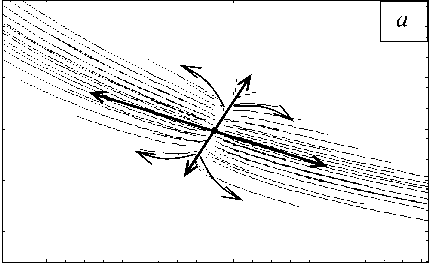
Вычислим корни характеристического уравнения, соответствующего системе (15), и найдем его собственные векторы. На рисунке 6 показано расположение точек равновесия на фазовой диаграмме и классификация фазовых портретов в их окрестности. Все точки равновесия системы (15) являются неустойчивыми по Ляпунову и делятся на два типа: неустойчивый узел и неустойчивое седло. Причем одному значению напряжения соответствует два равновесных значения параметра поврежденности, отвечающие тому и другому типу точек равновесия. На рисунке 7 представлены характерные фазовые траектории в окрестности типичных равновесных точек при различных начальных условиях, полученные численным интегрированием.

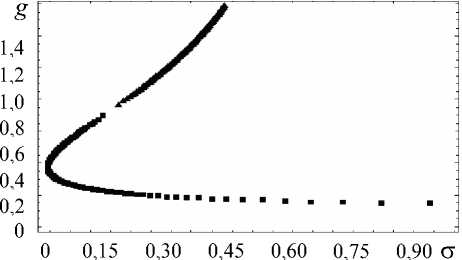
Рис. 6. Фазовая диаграмма и классификация фазовых портретов в окрестностях точек равновесия: ■ – неустойчивый узел, ▲ – неустойчивое седло

g

0,5

0,4

0,3

0,2

0,60      0,70      0,80      0,90 h

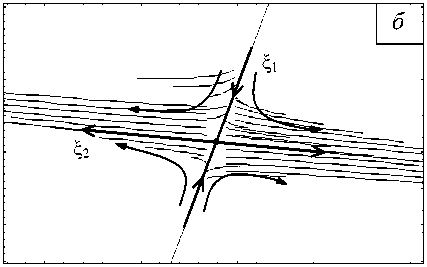
Рис. 7. Фазовый портрет в окрестности неустойчивого узла ( а ) и неустойчивого седла ( б ) (стрелками показано направление фазовых траекторий, ξ₁ и ξ₂ – сепаратриссы седла)

1,20

1,10

1,05

1,00

g

1,25

0,83      0,84      0,85      0,86 h

Рассматриваемая система (15) имеет два характерных участка фазовых траекторий: монотонное уменьшение амплитуды при увеличении размера структуры; резкое увеличение амплитуды при уменьшении размеров структуры. Важно отметить, что траектории второго типа являются траекториями LS-режима для параметра поврежденности. Таким образом, в случае квазихрупкого материала пространственно-локализованная симметричная структура p может эволюционировать в режиме с обострением, которому присуще уменьшение характерного размера этой структуры.

• 3.    Заключение

Проведенный качественный анализ кинетического уравнения, следующего из решения статистической задачи эволюции дефектов в квазихрупком материале, позволил установить типы точек равновесия, характерные фазовые портреты в их окрестности и зависимости амплитуды и координаты полуширины одиночной симметричной локализованной структуры от величины приложенного напряжения. Результаты получены для произвольного начального положения системы и уровня приложенных напряжений с учётом точной аппроксимации неравновесной свободной энергии.

Использование физически обоснованного представления для неравновесной свободной энергии позволяет утверждать, что квазихрупкое разрушение может быть представлено набором автомодельных решений квазилинейного параболического уравнения LS-типа, описывающим неограниченный рост плотности дефектов на уменьшающемся пространственном масштабе.

На основе метода усреднения показано, что малое возмущение приложенного поля напряжения способно вывести одиночную диссипативную дефектную структуру из положения равновесия с последующим обострением на уменьшающейся пространственной области. Учет условия ограниченности макроскопической деформации, аналогичного условию «выгорания» в теории горения [11], приводит к формированию ансамбля макроскопических дефектов — очагов макроскопических трещин и их последующему слиянию.

Исследования выполнены при поддержке Программы Президиума РАН «Фундаментальные проблемы механики взаимодействий в технических и природных системах» № 09-П-1-1010 и РФФИ (проект № 10-05-96065-р_Урал_а).