Некоторые классы мероморфных функций
Автор: Меликов Х.Х.
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.1, 1999 года.
Бесплатный доступ
Короткий адрес: https://sciup.org/14317979
IDR: 14317979 | УДК: 517.54
Текст статьи Некоторые классы мероморфных функций
Пусть S — класс функций вида
(1.1)
которые регулярны в области 5о = Т'\{О} = {г:О< Ц < 1} с простым полюсом в точке z = 0 и вычетом равным 1.
Пусть Es подкласс S, состоящий из однолистных функций в Eq. Функция f(z) Е Уз называется мероморфно-звездообразной, если Т { — ^(^ } > 0. Через X* обозначим класс всех мероморфно-звездо- образных функций.
Функция f(z) Е Es называется мероморфно-звездообразной порядка а, если
--I > а для всех z Е Eq и для некоторого а (0 ^ а < 1). Класс мероморфно-звездообразных функций порядка а обозначим через Е*(а).
Через У* Др,арр 0 < а < 1, 0 < р < 1, обозначим класс функций вида (1.1), удовлетворяющих условию гД^/ДД + 1
«аДДШ1^ - 1
<Р ДЕ ЕД.
Через У* Дар — 1,2/3 — 1) обозначим класс мероморфно-звездообразных функций порядка а и типа р, которые удовлетворяют условию
2.ДДДДД + 1
< 1
для всех z Е Ео и для некоторых а и р (0 < а < 1, 0 < р < 1).
Заметим, что S*( —1,0) — класс функций /(г) = | + ^2 ак^к, которые удовлетворяют условию
Ц/'Ц)//Ц) + 1|<1.
Введем класс Х*(А,В) следующим образом:
zf^ _ 1 + Aw(z)
f(z) 1 + Bw(z) ’
(1-2)
где — 1 < А < В < 1, w(z) — функция, регулярная в Е и удовлетворяющая условиям: w(0) = 0, w(^) < 1, если \z\ < 1.
Заметим, что Е*( — 1,1) = И*, S*(2a — 1,1) = Н*(а).
Класс Н*(а) рассматривали Pommerenke [11], Clunie [3], Miller [9] и другие. Класс И*(2а/3 — 1,2/3 — 1) был введен Aouf М. К. [1], Mogra, Reddy и Juneja [10]. Интегральными преобразованиями класса И* (а) занимались Л.В.Зарудняк [6] и Goel и Sohi [5].
Пусть /(г) = | + auzn и д(г) = | + Ьп принадлежат классу И. Тогда произведение Адамара функций /ид определяется равенством
U * дН^ = - + а^и^\ z z—‘
Z Е Eq.
Пусть
fc=l
Далее, пусть МДА, В) — класс функций вида (1.1), которые удовлетворяют условию
Рп+1/(г) п + 1 + ДВ + A)w(z)
Dnf^ (n + 1)(1 + Bw(^))
(г G Eq),
(1-4)
где n G No = {0,1, 2,... }, — 1 < A < В < 1, w(z) — функция такая, как в (1.2).
В работе будут рассмотрены основные свойства класса МДА, В): критерий принадлежности функции f(z) к классу РДА,В), оценки коэффициентов, интегральные операторы и ряд других вопросов.
2. Класс МДА, В)
Теорема 2.1. Пусть f(z) = - + 52 akzk принадлежит классу РПД,ВУ Тогда круг w(^) ^ г < 1 отображается функцией F = Рп+1/(г)/Рп/(г) — 2 в круг
где
\F-a\^d, (2.1)
1 — Вет2 (В — с)г пВ + А
1 — B2r2 ’ 1 — В2г2 ’ п + 1
Доказательство. Из определения класса Ми^А,В^ имеем
F =
^^^^^^^™
n + 1 + (пВ + А)гв(г)
(п + 1)(1 + Вги^г^
1 + сго^г)
1 + Bto^z')
(2.3)
Из (2.3) получаем
F _L 1
ирг) =--— -Д |F + 1|2 < 3\сВВГУ c + BF
ИЛИ
1 — Вег2
1 - В2г2
<
^В-срг2
(1 - в2^2'
(2.4)
Из (2.4) следует (2.1).
Теорема 2.2. Пусть f^F) = 7+52 akzk принадлежит М^А^ВУ Тогда для г < г < 1 верны оценки n + 1 — ^пВ + А)г Г Dn+1 f(z) 1 n + 1 + ^nB + A)r
—;----7Т73---^—;—л 1 —т;— т,—;-- 2 > -------—— ---——;—
---------------------------- П, А ---------------- -- / \-- (n+l)(l— Вт) ( Dnf(z) J (п+1)(1 + Вг)
Результат следует непосредственно из теоремы 2.1.
Следствие 2.1. Пусть f^ Е М0(Л,В) = И*(И,В). Тогда
1-Аг f zf^\ 1 + Аг
1 — Вт ( /(г) ) 1 + Вт
(2-5)
Теорема 2.3 [1]. Пусть f^ Е ЕДА, В). Тогда на Д = г < 1 имеем
Х — ВгУ®-^/® м угЦВ-АДВ
< 1/(^)1 <
(2-6)
если В У О,
- ехр Аг < /Д) < -ехр(—Аг),
(2-7)
если В = 0.
Результат теоремы 2.3 следует из (2.5), если сначала вычесть из частей неравенств по 1, а затем разделить на z и проинтегрировать по z от 0 до г. Функция /(г), определенная равенством показывает, что оценки (2.5)—(2.7) точные.
Давая частные значения А и В, класс МП^А,В) будет сводиться к известным подклассам звездообразных мероморфных функций: Мп = Мп( — 1,1), Mn^a) = Mn(2a — 1,1), Mn[a] = Mn{ — a, a), Mu^— p, «3Y Mn^2«3 — 1,2/3 — 1).
Следствие 2.2. Пусть f (z) = ^ + 52 akZk принадлежит Mn. Тогда Z k = l n + 1 - рг - г пп+1у^^ 2I < n +1 + (n - i)r (n + l)(l — r) ( Dnf(z) J (n + l)(l + r)
При п = 0 имеем
1 + г
1 — г
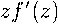
Чтйг}
1 — г (1 — г)2
<--, ------—
1 + г г
(1 + г)2
< ^н^ < ——
Следствие 2.3. Пусть f^ = ~ + 52 akZk принадлежит Mn(a). Тогда 2 к = 1
п+1 — (п—1 + 2а)г < Г Du+1 f^ 1 < n+l + (n—1 + 2a)r
(n+l)(l— r) ( Dn/(^) J (n+l)(l+r)
1 - (2a - l)r
1 — r
zf^ ) < 1 + (2a - l)r f^ J 1 + r
^W)}^
Следствие 2.4. Пусть функция / (г) = - + 52 akZk принадлежит М„[а]. Тогда 2 k=l
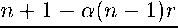
(n + 1)(1 — ar)
_ 91 < ™+l + a(77-l)r
( D^z) J ^ (n+ 1)(1 +ar)
-
1 +«r < ^ Г 1 < 1 - ar
1 — ar ( /(г) J 1 + ar’
<1-^ < Я№)} < (l±2til
Следствие 2.5. Пусть f^ = - + 52 akZk E Mn( —p, app Тогда 2 k = l n + 1 — ppict — l)r ( Dn+1f(z) 1 < n + 1 + ppict — l)r рг + 1)(1 — apr) ( Dnf(z) J pi + 1)(1 + apr)
1 — apr ( /(г) J 1 + apr’ (l-aPr^'“ ^ ^^ ^ (l^a^r/^l r r
Следствие 2.6. Пусть f^z') = 7 + 52 akzk E Mup2aP — 1, 2/3 — 1). Тогда 2 k = l n + 1 — [n(2/3 — 1) + 2a/3 — l]r / j' Dn+1 f^z) o) n + 1 — [n(2/3 — 1) + 2a/3 — l]r (^+1Жч2^пя ”2J (2ГПЖТ(2^1Я
_ 1 - (2a/3 - l)r J zfPz^ ) 1 + ^gp - l)r
!-(2/3-l)r l/(^)J" l + (2/3-l)r’
2/3(l-a) 2/3(l-a)
(1-^-1))— c $№)} e (1 + W-1W^
-
3. Теорема включения
Теорема 3.1. Пусть f(z) = 7+52 ak^k G М^А^ В). Тогда Mn+i(A, В) С МДА, В) для любого п Е No = {0,1,2,...}.
Доказательство. Пусть функция f (г) Е МДА, В). Тогда, согласно теореме 2.2, для г < 1 имеем
п(1 — В) + 1 — А Г Р^Ч^ _ а < п(1 + В) + 1 + А
(п + 1)(1-В) " } Р-НЧ (п + 1)(1 + В) ' 1 ;
При фиксированном А и В функция - "^"^(^ij4 возрастает с возрастанием п, а функция - ^^^д)4 убывает с возрастанием п. Поэтому
п(1-В) + 1-А (п + 1)(1 - В) + 1 - А (Pn+2fH о}
(n + l)(l-B) < (n + 2)(l-B) \P"+4^ J
(n + 1)(1 + В) + 1 + А п(1 + В) + (1 + А)
(n + 2)(l + B) < (IV+ !)(! +В) '
Из последних неравенств и следует справедливость утверждения.
Следствие 3.1. Справедливы следующие включения:
Мг+1(а) с МДД, АД+iN С МД«], Мг+1(-^,а^) с МД-р,ДД Mu+^ap - 1,2/1 — 1) С МД2сф - 1, 2/3 - 1), n Е No = {0,1,2,... }.
Из теоремы 3.1 и следствия 3.1 следует, что классы функций МДА, В), Mn(a), ,Мп[а], Мн\—3, а/3], Mn (2a^ — 1, 2/3 — 1) являются подклассами однолистных функций.
-
4. Интегральные операторы
Теорема 4.1. Пусть функция /(^) = 7 + 52 akzu для данных n Е No и с > О удовлетворяет условию
(р^нч а 1-д(1 + в) + (1 + А)](с + 1) t Pnf4) J (n+l)(l + B)(c+l)
(4.1)
Тогда, функция
z
F<4
Cf^dt
(4.2)
принадлежит Mn(A, В) для F^ 7^ 0 в Eq.
Доказательство. Используя тождества z^PnF4W = сРпНЧ - (с+ l)DnF(^),
(4.3)
z(,DnF^Y = (n + l^Dn+1F^ - (n + ^DnF^, условие (4.1) можно записать в виде
(4-4)
(4.5)
( ^n+Dn+iF^ - (n + 2 - с) ) 1 - [п(1+ В) + (1 + Л)](с+ 1)
|n+l-(n+l-c)^L Р (n + 1)(1 + В)(с + 1)
Мы должны показать, что неравенство (4.5) сводится к неравенству (см. теорему 3.1)
Л ^У^) _ J , п(1 + В) + (1 + Л)
I D^ / (п+ !)(! +В) •
Определим w(z) в Е через
221ТМ = „+1 + |(,1 + 2)B-A]«W
Вп/(г) (n + 1)(1 + Bw(z))
Очевидно, что w(z) регулярна в Е и w(0) = 0. Нам надо показать, что w(z) < 1, z Е Е. Логарифмическим дифференцированием получаем
(п + 2) pn+i^j - (п + 2 - с) n + 1 + (пВ + H)w(^) Д7Г7^ТГЛ5^Е-- = "мЛиТТ^ЙГ
+ т--------(В^ЗДЙУ---——---. (4.7)
(п + 1)(1 + Bw(z))[(l + с^В — A]w(z) + с]
Если w(z) не удовлетворяет условию w(z) < 1, z Е Е, то по лемме Джека [7] существует точка ^oh ^о < 1 такая, что
^ow'f^o) = Kw^z0Y
(4-8)
где w(zo) = 1 и К ^ 1. Из (4.7) и (4.8) имеем
№
<п + 2)
£>" + 2F(z) №+1F(z)
— (n + 2 — с)
n + 1 — (n + 1
^^^^^^^™
с)
D>‘F(z) D>‘ + iF(z)
- 2 =
п + 1 + ^пВ + Л)гс(г0) (n + 1)(1 + Bw^zoy
(В - A^Kw^
(4-9)
^п + 1)(1 + Вгс(г0))[с + [(1 + с^В - Л]гс(г0)]
Таким образом, левая часть (4.9) больше, чем
1- (п(1 + В) + 1 + Л)(с+1)
(n +1)(1+ В)(с+1) ’ которое противоречит (4.1). Следовательно, w(z) < 1, и из (4.6) следует, что F^ Е M^A^Y
Полагая А = — 1, В = 1 в условиях теоремы 4.1, получаем следующий результат.
Следствие 4.1. Пусть f(z) G Мп для данных п G No и с > 0 удовлетворяет условию
^^^^^^^™
2Н
^^^^^^^™
2n(c+ 1)
п + 1)(с + 1)
Тогда.
Z
tcf принадлежит классу Ми для F^ ^ О в Eq. Следствие 4.2. Пусть функция f^ = ^ + ^ akzu для данных n G No и с > О удовлетворяет условию (П«утм_д<у^1 + *М1 (410) \ ЬНИ / 2(п + 1)(с+1) ■ Тогда функция Z F^ = ^i / Ff^dt (4.11) принадлежит классу Mn(a) для F^z) ^ 0 в Eq. Следствие 4.3. Пусть функция f^ = ^ + ^ akzu для данных n G No и с > О удовлетворяет условию ( D^f^ _ 1 1 - [n(l + а) + 1 - а](с+ 1) ( D-f Тогда функция Z F^ = / ff^dt ' ' тс+1 / х ' принадлежит классу Mn(a). Следствие 4.4. Пусть функция f^ = ^ + ^ akzk для данных п 6 No и с > О удовлетворяет условию №<^ Dn+1f^ D^f^ -2} 1 — [п(1 + а/1) + 1 — /3](с + 1) (п + 1)(1 + «ЗИС + 1) Тогда, функция F^ = Z 3jt-mdi о принадлежит Мп(~3, ар). Следствие 4.5. Пусть функция f(z) удовлетворяет условию = 7 + Е akZk для данных n G No и с > 0 fc=i С Пп+1^Ы { вч^ 2 Г 1 — 2р^п + а) (с + 1) ' 2/3(n +1)(с+1) ' Тогда функция F^ = MlW* о принадлежит классу Mn(2ap — 1, 2(3 — 1). При п = 0 из теоремы 4.1 получаем следующий результат Goel и Sohi [5]. Следствие 4.6. Пусть f^ = 7 + 52 akzk принадлежит Е* и удовлетворяет условию Г МЧАЛ 1 ^ ^5, оО. I ПИ J 2(с + 1) Тогда. F^ = FjBw» о принадлежит Е* для f(z) ^ 0 в 0 < 7 < 1. При п = 0 в условиях теоремы 4.1 получаем следующий результат Goel и Sohi [5]. Следствие 4.7. Пусть f^EXi удовлетворяет условию 4' Тогда. Z Ff^dt принадлежит Е* для F(z) ^ 0 в 0 < 7 < 1. Следствие 4.8.Если f(z) = 7+52 ak^k G ^*^А,В), то z F^ = M‘‘№dl будет принадлежать классу Е*^А,ВУ При п = 0, А = p^2a — 1) и В = /3, где 0 < а< 1, получаем результат Mogra, Reddi и Juneja [10]. Теорема 4.2. Пусть / Е Mn^A,BY тогда рИ = — У t"+1JWdteMn+MB^ для F^ ^ 0 в О < г < 1. Доказательство. Имеем сПпД^ = (n + l)Pn+1F(^) - (n + 1 - c^DnF^ И cDn+1f^ = (n + ^Dn+2F^ - (п + 2 - c)Pn+1F(^). При с = n + 1 из этих соотношений получаем VnP^D^F^ -Dn+1F^ _ D'1^1^ (?7+ ДГ^+^Д “ Dnf(z) ’ которое сводится к (77 + 2) Dn+2F(z) 1 _Dn+1f^ (77 + 1) D^F^ 77+1 “ Dnf(z) ' Таким образом, в соответствии с (3.1) имеем V + ID^F^ 77 + 1 J \ D^f^ / (п + 1)(1 + В) ' Из последнего неравенства следует, что г_ 21 < (п + 1)(1 + в) + 1 + и \Dn+1F^ J (п + 2)(1 + В) ' Это завершает доказательство теоремы. При А = — 1, В = 1 из теоремы 4.2 следует результат Ganigi и Uralegaddi ([4],Т.З). 6. Класс РП(А,В) Через РДА,В) обозначим подкласс функций класса МДА, В) вида СХЭ /(г) = - + ak ^ О с неотрицательными коэффициентами. Теорема 6.1. Пусть функция / (Д = - + 52 ак^к, ak ^ 0, регулярна в Ео = {z : О < Д < 1}. Тогда f(z) Е Рп^А,В) тогда и только тогда, когда (п+ 1)(77 + 2)...(77 + 1 + ^)Д(1+В) + 1+Л] > ---------------------------------------------------------- Л. 1 nil -1 < А < В, 0 < В< 1. ДОКАЗАТЕЛЬСТВО. Предположим, что функция/(г) принадлежитРп(А, В). Тогда из (1.4) имеем (п + 1)(Ри+1/(Д -ВИ/(Д) В^Дг^ + 2)В - А] • В^+ДД) • (п + 1)В Из этого неравенства получаем (п + 1)[а0 + Е МДД±Д^±1±М^Д] _____________________fc=l____________________________________ (S-A)l- Е ^±^±ti±M^ fc=l Так как ;R{w} ^ |w для любой функции го, то имеем № ОО \ ОО в - А - Е (21±1М21Мт_Д±1±Д(ВА: + AV k=l < 1. (6-2) Выбираем значение г на вещественной оси, чтобы знаменатель был вещественным. Очевидно, знаменатель будет принимать вещественные значения и при г —> О по вещественной оси. Так как при г = 0 знаменатель положителен и непрерывен и |w(^) I < 1, то знаменатель принимает только положительные значения при г > 0. Устремляя г —> 1, после упрощения из (3.2), получаем (3.1). Обратно, предполагая, что (3.1) верно для всех допустимых значений А и В, имеем ф^дв^д = Un+lHDn+1H^-DnH^HW^B-AWH^-^A^BDn+1H^\ п + 1) \ (п + 2) (п + 3) ... (п + 1 + /г) ^. t«o + £' Л ' 'ак^ к=1 . .. 1 ' (п + 1)(п + 2)...(п + 1 + А;) ^^^^^^^™ (в +z Е ЕД чвк + Aw11 или ДВ-А}- (n + 1) (п + 2) ... (n + 1 + /с) Так как полученное неравенство верно для всех Д = г, 0 < г < 1, то, устремляя Д —> 1, имеем (n + 1)(п + 2) ... (n + 1 + /Д[А:(1 + В) + 1 + А] о (к + 1)!(В - А) а-k< 1- Отсюда следует, что f(z) принадлежит классу РДА,В) Заметим,что Pq^A,B) = ^ЧА,В\ Следствие 6.1 [2]. Функция f(z) = - + 52 akzk, ak ^ 0, принадлежит классу 2 к=1 ^^А^В) тогда и только тогда, когда ^W + В) + 1 + A^ak ^ В - А. к=1 Результат точный для функции . / х 1 В - А к fk^ " z + k^ + BHl + A2 ' Заметим, что для класса Р^^А^^ верны теоремы 3.1 и 4.1 в силу того, что РП^А,В) является подклассом МП^А,В\ 7. Радиус выпуклости Теорема 7.1. Пусть функция f^ = - + 52 akzk принадлежит классу Ри^А,ВУ 2 к = 1 Тогда f(z) мероморфно выпуклая порядка б (0 < б< 1) в круге \z\ < г = г (Л, В, п, 5), где ЛЛ.В,^ = inf 1(" + 1)1,1 + А-'. Д ТД, - Д + л|11 ~51 к-^1 ( (В — А^к^к + 2 — б)(к + 1)! Результат точный. Доказательство. Достаточно показать, что 2 + ^rv^ ид ^^^^^^^™ б для г ^ т^А,В,п,,б\ Имеем 2 + ^rv^ f'^ 52 (^ + ^akzk 1 к=1 72 - 52 kak-zk"1 к = 1 £ ЦкР^акМ^ к = 1_____________________ 1- £ kak\z\k^ к = 1 Оно ограничено числом 1 — б, если ^>А±НАаь1гГ1 к = 1 < 1. (7.1) Так как функция f(z) Е Р„(Л,В), то из (6.1) следует, что (7.1) будет верно, если Цк + 2 5) |_|fc+i < (п + 1)(п + 2) ... (n + 1 + &)[&(! + В) + 1 + Л] 1 - б (,В-АПк + 1у. т. е. если J (n+^)(n + 2)111(n+J_H)^ t (B-A)fc(fc + 2-5)(fc + l)! J ’ ) Полагая г = r(A,B,n,5) в (7.2), получаем результат. Результат точный для функции __I___________________________zk k > 1 z (n + 1) (п + 2) ... (n + 1 + &) [&(1 + В) + 1 + А] ’ / При п = О, получаем следующий результат. Следствие 7.1. Пусть функция /(г) = | + a^z + a2z2 + ..., а^ > О принадлежит Т,*(А,В). Тогда f(z) мероморфно выпуклая порядка б, 0 < б < 1, в круге \z\ < трА, В, 5), где т^В^^ = inf М1-б^Ц1 + ВН1 + АП^ t (В- A)k(k + 2 — 6) J ' Результат точный для функции В-А к(1 + В) + 1 + А (О1). Следствие 7.2. Пусть функция / (г) = - + 52 akZk принадлежит классу И*(а), z fc=i т.е. классу мероморфно звездообразных функций порядка а. Тогда она мероморфно выпуклая порядка б (0 < б < 1) в круге г < г = г(а, 5), где ( J (1-5)(1 + 5) г а, о = inf < ------——-------— > . k^i [ (1 — a^k^k + 2 — 5) J Результат точный. Следствие 7.3. Пусть функция f^ = - + 52 akzk принадлежит классу к = 1 X* (—p,ap), 0^а<1, 0<Р^1, тогда она мероморфно выпуклая порядка б (О < б< 1) в круге \z\ < г = г(а,р,б), где r^P^ = inf ^^^^^^^ j>k+1 . Результат точный. Следствие 7.4. Пусть функция f^z') = - + 52 akzk мероморфно звездообразная порядка а и типа р. Тогда она будет мероморфно выпуклой порядка б (0 < б < 1) в круге г < г = r(a, Р, 5), где I ц f J “ 5^k + “) U+1 г а, Р, о = inf < -----——-------— > . k^Y I (1 —a)k(k + 2 — 5) J Результат точный. 8. О свертках в классе Р^А, В) Теорема 8.1. Пусть функции J ^ = -+ ^2 ak^k и д^ = -+ ^2 bkzk принадлежат к = 1 к = 1 классу Pn(A,B), п ^ 0. Тогда U * в)И = | + ^akbkzk также принадлежит Pn(A,B), п ^ 0. Доказательство. Пусть /(г) и д^ принадлежат классу РП^А,В\ Тогда по теореме 6.1 имеем '—тдтш^л—'№ + с) + 1 + л|о‘ < *' Так как f(z) и д^ регулярны в Eq = {г : 0 < г < 1}, то (/ * g^z) регулярна в Eq. Далее имеем (п + 1)(п + 2) ... (n + 1 + &)[&(! + В) + 1 + А] + 1)!(S —А) < [ (п + 1)(п + 2) ... (n + 1 + &)[&(! + В) + 1 + А] I (^ + 1)!(В-А) Ф Ьк < (n + l)(n + 2) ... (n + 1 + &)[&(! + В) + 1 + A] (fc + 1)!(S - A) (n + l)(n + 2) ... (n + 1 + &)[&(! + B) + 1 + A] (/c + l)!(B-A) bk< 1. По теореме 6.1 (/ * g^z) E Fn(A,B). При n = 0 из теоремы 8.1 следует результат N. Е. Cho [2].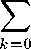
Список литературы Некоторые классы мероморфных функций
- Aouf M. K. On the coefficients of some meromorphic classes of order $\alpha$ and type $\beta$//Rend. math. e appl.-1988.-V. 8, № 2.-P. 211-221.
- Nak Eun Cho. On certain class of meromorphic functions with positive coefficients//Math. Jap.-1989.-V. 34, № 6.-P. 901-907.
- Clunie J. On meromorphic schlicht functions//J. London Math. Soc.-1959.-V. 34.-P. 215-216.
- Ganigi M. R., Uralegaddi B. A. New criterio for meromorphi univalent functions//Bull. math. Soc. math. R.S.R.-1989.-T. 33(81), № 1.-P. 9-13.
- Goel R. M., Sohi M. S. On a class of meromorphic functions//Glasnic, Mat.-1982.-V. 17(37).-P. 19-28.
- Зарудняк Л. В. Об интегральном преобразовании некоторых классов мероморфных функций//Экстремальные задачи теории функций.-Томск, 1986.
- Jack I. S. Functions starlike and convex of order $\alpha$//J. London Math. Soc.-1971.-V. 2.-P. 469-474.
- Juneja O. P., Reddy T. R. Meromorphic starlike univalent functions with positive coefficients.
- Miller J. E. Convex meromorphic mappings and related functions//Proc. Amer. Math. Soc.-1970.-V. 25.-P. 220-228.
- Mogra M. L., Reddy T. R., Juneja O. P. Meromorphic univalent functions with positive coefficients//Bull. Austral. Math.-1985.-V. 32.-P. 161-176.
- Pommerenke Ch. On meromorphic starlike functions//Paccific. J. Math.-1963.-V. 13.-P. 221-235.


