Некоторые обобщенные интегральные преобразования и их обращения

на случай, когда ядро содержит гипергеометрическую функцию Райта [3]:

p ^ q ⁽z ^} — p ^ q

^(a i ^{; a} i ⁾ 1,p ^(b j ; ^e j ) 1q

z , где

z E C ; a i , b j E C ; a i ,e j E R = (-то, +^); (a^ j = 0; i = 1, 2, ...,p; j = 1, 2,..., q).

Представление функции _p Ф _q с помощью интеграла Меллина — Бернса имеет вид [3]

, r(s) п r(a i - O i S)

р Ф , (z) = T" -^ ---------- (-z ) ^-s ds,               (3)

²ⁿi lL   п r(b j - e , S)

j =1

где s Е C , а L _-7 — контур, проходящий от точки —то + i^ 1 до точки —то + i^ 2 (-ТО < ^ 1 < ^ 2 < +то) .

Рассмотрим следующие обобщенные интегральные преобразования:

Г(с) 7 x               и,т );(1,Y)          x ²

P 1 ^{{f (x)}; У^} =             ₂ , ₂^{f (х)} 2 ^ф 1                    ^—b 2 I 2 dx, ⁽⁴⁾

Г(а) J x ² + y ²                (с, в)         \x ² + y²/

Pt«,Y.i ₌ M 7 x « _г1ФГ (a-т );(1.Y)    J y ² V ^Y

P 2 {/^{(х) y}} r(a)J x ² + y ² f ^(х) 2 ^Ф 1 [     (с.в)       b^ 2 + y²) Jdx ⁽⁵⁾

∞

c              ^Г(с)    7 ^f(x)    Ф [ ^(а,т Wy )    J ^x V1 .     z₆₎

G p ^{{f (x)};^y}   г(а)Г(р) J (x + y) p ^ 2 ^ФЦ     (с,в )       bU + у) Г d^{X.     (6)}

При b = 0 наши преобразования (4), (5), (6) совпадают с классическими преобразованиями (1), (2).

Теорема 1. При условии существования и абсолютной сходимости интегралов (4), (5), (6) имеет место следующее равенство

∞

∞

x p^l {f (t); x} g(x)dx = j X.P 2 {g(t); x} f (x)dx.

Это равенство является обобщением равенства (2) в [4].

Интегральные преобразования P 1 {f (x); y } и P ₂ {f (x); y } можно рассматривать как композицию обобщенных интегральных преобразований Лапласа

∞

-L i ^{{f (x)}; y^} = I e^-xy

1 Ф ^т ; ^в (a; c; -( (xy)¹ ) f (x) dx,

∞

L 2 {f (x); y} = [ xe^-: x’y

• 1 Ф Т ^{; в} ( a; c; — b ( x ² y ² ) ^Y ) f (x) dx,

∞

L 2

^{{f (x)}; y^} = I 0

xe^ - x⁴’ f (x) dx.

В равенствах (8), (9) 1Фрв(a, c, z) есть обобщенная конфлюэнтная гипергеометри- ческая функция [5], [6]

1 Ф ^т’^в (a,c,z) =

FGa)^ /^{t a- 1 (1 - t) C-}“^-1- * i

( c, т ) ( c, в )

|zt ^T dt,

где Re c > Re a > 0; {т, в} C R; т > 0; в- > 0; т — в < 1; r(a) — классическая гамма-функция [1].

Теорема 2. При условии существования и абсолютной сходимости интегралов имеют место равенства

1 ~

L2 {L2 {f (x); u} ; y}    2 P2 {f (x); y} ,

L2 {L2{f (x); u}; yj = 2 Pi{f (x); y}.

Доказательство теоремы отражено в работе [5].

Выведем формулу обращения для интегрального преобразования (4). Пусть

Pi {f (u); x} = g(x).

Применим к обеим частям равенства (13) преобразование Меллина

∞

M

{ f (x); s} = j x ^{s- 1} f (x)dx.

Учитывая, что M

{ -P i ^{{f (u)};^x}; s} =

∞

=/ x ’^{- 1}

∞

Г(с) [

Г(а) J

u x2 + u2

f (u) • 2 * 1

^(a,T); ^(1,y ) ^(c, ^e)

— b

/   u ²

\ x ² + u ²

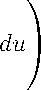
dx =

Г(с)

Г(а)

∞

∞

I uf ^(u) и

x s - 1

x ² + u ²

2 * 1

^(a,T); ⁽i,y ) ^(c,e)

—b

u ²

x ² + u ²

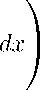
du =

1 Г(с)Г (j)

2 Г(а)

• 2 ^ 1

^(a,T);⁽¹ - j ,Y) ^(c,^e)

получим M {g(x); s} = ^(Г^) ² ) • 2 Ф 1

Отсюда имеем

^(a,T);⁽¹ - j ,Y) ⁽c,^e)

• M { f (u); s},

— bl • M { f (u); s} .

M {f(u); s} = 2?7r(a7-;T (2»1 [ (a,T);(1,— j,Y) — bll • M {g(x); s} .

Г(с)Г ^2J (       |_         (c,e)_| J

Применяя известную формулу обращения для преобразования Меллина [2], получим

∞

2r(a) f -1

f (u) =

у(ф J x g(x)6 u-j dx, 0

σ + i ∞

2 П7 / Z ( S ) ds-Z(s)=^r Й) • 2 * 1

σ - i ∞

где 0(x)

^(a,T);^{(1 —} j ,y ) (с,в)             bj.

Равенство (16) есть формула обращения интегрального преобразования (4). Аналогично получается формула обращения для преобразования (6).