Некоторые оценки G-емкости экстремальных поверхностей и следствия из них

В процессе развития теории капиллярных поверхностей появились функционалы с нелинейной функцией, зависящей от единичной нормали к поверхности, которые отличаются от функционалов объема, и потребовали дополнительного исследования для получения признаков устойчивости и неустойчивости. В частности, в монографии Р. Финна [14] рассматриваются вопросы устойчивости капиллярных поверхностей, а в работе В.А. Саранина [12] изучается устойчивость так называемых магнитных жидкостей, которые приводят к рассмотрению функционалов вида

F (M) =  Ф(х,£) dM

M

где Ф : R n ⁺¹ х R n ⁺¹ ^ R — C ² — гладкая функция, в качестве потенциальной энергии соответствующей физической системы.

Подобные вопросы также тесно связаны и с физическими задачами о равновесии различных систем и описании их устойчивых и неустойчивых состояний. В большинстве случаев решение сводится к исследованию положительной определенности второй вариации специального функционала, связанного с потенциальной энергией системы. Примерами такого функционала будут функционалы, являющиеся линейной комбинацией функционала площади и функционала объема, что приводит к исследованию поверхностей постоянной средней кривизны, которые моделируют, например, равновесные состояния двух жидких сред.

В настоящее время достаточно полно подобные исследования проведены для одномерных функционалов и для функционала площади. Имеется широкий спектр работ, посвященных задаче об устойчивости минимальных поверхностей в евклидовом и псевдоевклидовом пространствах, в частности, А.А. Тужилина, Ю.А. Аминова, А.Т. Фоменко, В.М. Миклюкова, В.А. Клячина, В.Г. Ткачева, А.В. Погорелова, М. до Кармо, Ч.K. Пенга, Ш. Яу, Р. Финна, Дж. Саймонса и др.

Для решения некоторых задач теории минимальных поверхностей были применены модульно-емкостные методы. Эти методы заимствованы из теории квазиконформных отображений и модифицированы В.М. Миклюковым [7] применительно к исследованиям минимальных поверхностей. Позже, в работах В.М. Миклюкова и его учеников, модульно-емкостная техника дала эффективные результаты для изучения минимальных трубок и лент в евклидовых и псевдоевклидовых пространствах (например, [9; 10]), для определения конформного типа поверхности (например, [5; 8]), а также для исследования устойчивости поверхностей нулевой средней кривизны (и, в частности, трубок и лент) в евклидовых и псевдоевклидовых пространствах (например, [2; 4]). В данной работе эти методы применяются для исследования устойчивости экстремальных поверхностей.

Постановка задачи. Пусть M — n-мерное связное ориентируемое многообразие класса C ² без края. Рассмотрим гиперповерхность M = (M, u) без края, полученную C ² -вложением u : M ^ R n ⁺¹ , и C ² -гладкую функцию Ф : R n ⁺¹ ^ R , С Е R n ⁺¹ , Ф(-£) = Ф(£). Если обозначить через С поле единичных нормалей к поверхности M, то для любой C ² -гладкой поверхности M определена величина

F (M) = /ф(£ )

M

dM,

которая не зависит от выбора нормали ξ. Функционал (1) будем называть функционалом типа площади .

Основным объектом данного исследования будут поверхности, являющиеся экстремалями функционала (1). Заметим, что при Ф(£) = 1 экстремали функционала — минимальные поверхности.

Цель работы: получение признаков устойчивости и неустойчивости экстремальных поверхностей M.

1.    Основные понятия

Пусть V — C ² -гладкое векторное поле, определенное в окрестности поверхности M, такое, что V| м = h-C, где h Е C q ( M ), С — поле единичных нормалей к поверхности, при этом предполагается, что интегральные кривые поля V лежат на прямых линиях и вдоль них выполнено |V| = const.

Ясно, что если поверхность M вложена, то любое векторное поле V = h£, заданное вдоль M, можно продолжить в некоторую окрестность M так, что будут выполнены сформулированные выше условия. Заметим, что согласно работе [15] вторая вариация не зависит от выбора продолжений.

Пусть U (M) — окрестность поверхности M, в которой определено поле V и однопараметрическая группа локальных диффеоморфизмов g _t (x) : U (M) ^ R ⁿ⁺¹ , порожденная векторным полем V. То есть g _t (x) — решение задачи Коши:

dgdtx ) = V(g t (x)), g t (x)| t =0 = x.

Положим M t = g _t (M). Ясно, что M 0 = M.

Определение 1. Поверхность M является стационарной , если первая вариация функционала (1) равна нулю, то есть

1 / Ф«) dMt dt t=0

= 0.

M t

Определение 2. Стационарная поверхность M будет устойчива , если вторая вариация функционала (1)

№ Р^{( )} dM t

Mt t=0

знакоопределена при всех бесконечно малых деформациях M t поверхности M, иначе поверхность M — неустойчива .

Замечание. В случае когда вторая вариация стационарной поверхности локально знакоопределена, то есть вариации с малым носителем дают одинаковый знак, будем называть поверхность экстремальной . Далее будут рассматриваться только экстремальные поверхности.

Обозначим G — квадратичную форму, соответствующую матрице

G ij    dC i de j + ⁵ ij ^{(ф ( DФ,}^ ^’

δ _ij — символ Кронекера, k _i — главные кривизны, а E _i — главные направления поверхности M .

В работе [3] была доказана следующая теорема.

Теорема 1. Поверхность M класса C ² является экстремалью функционала (1) тогда и только тогда, когда

n

Е k i G(E i ,E ) = 0.

i =1

Экстремальная поверхность M устойчива, если для любой функции h(x) Е C q ( M ) знакоопределена квадратичная форма

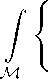
G(^h, Vh)

^^^^.^^^^^

К2 5П^ k^G^Ei,Ei) dM, i=1

иначе поверхность M неустойчива.

2.    Оценка G-емкости, проективный объем и неустойчивость экстремальной поверхности

Общеизвестен тот факт, что гауссово отображение двумерных минимальных поверхностей в единичную сферу является одновременно гармоническим и конформным.

В многомерном случае это уже не так. Поэтому в [16] был найден другой подход к изучению полных многомерных минимальных подмногообразий евклидова пространства произвольной коразмерности. Суть данного метода сводится к введению некоторой меры некомпактности (проективного объема) минимальных подмногообразий евклидова пространства. В работе [13] этот метод применен к задачам исследования внешней геометрии многомерных минимальных поверхностей.

В настоящей работе описанный подход был использован для получения признака неустойчивости экстремальных поверхностей.

Поверхность M (без края) называется внутренне полной , если любой расходящийся путь на M имеет бесконечную длину.

Поверхность M называется внешне полной , или собственно погруженной, если для любой последовательности точек {m i } С M, не имеющей накопления в M , последовательность образов x(m i ) не имеет точек накопления в R n .

Пусть Q С M — произвольная область на поверхности M и P,Q С Q — два непересекающихся замкнутых множества в Q. Всякую такую тройку (P, Q; Q) назовем конденсатором на поверхности M.

G-емкостью конденсатора (P, Q; Q) (см. [4]) назовем величину capG(P,Q;Q) = inf j G(VV, Vr)

dM,

M где точная нижняя грань берется по всем локально-липшицевым функциям r : M ^ R1 таким, что ^(m) = 1 при m Е P и ^(m) = 0 при m Е Q.

Рассмотрим на поверхности M, являющейся экстремалью функционала типа площади (1), два замкнутых непересекающихся множества (см. рис. 1): P — часть поверхности, содержащаяся внутри шара O 1 (O,r), и Q — часть поверхности, лежащая вне шара O ? (O,R), то есть Q = M \ O ? (O,R), где 0 < r < R <  то, на которых функция h(u) такая, что h| _P = 1 и h| Q = 0.

Несобственный интеграл

^{Q ( M}> = / W                   ⁽³⁾

M называется проективным объемом поверхности M.

Обозначим

n

HAN G = Ek ? G(E . -E . ).

i =1

A(£) — максимальное по модулю собственное значение матрицы G, и

V m = У

M ( r,R )

d M —

объем части поверхности M.

Теорема 2. Внешне полная экстремальная поверхность M(r,R) имеющая конечный проективный объем, будет неустойчива, если выполнено неравенство

[ ||A|| G dM >      QTvME²''E

(ln R ) ²

M ( r,R )                      ^r

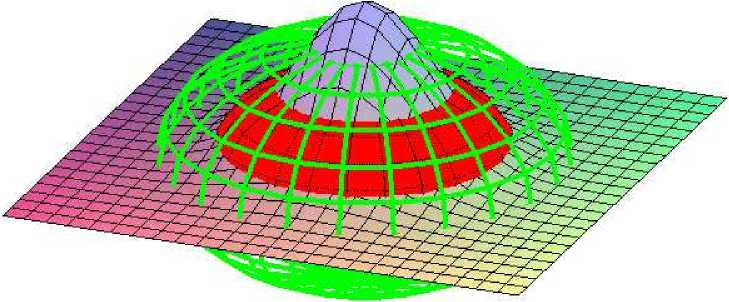
Рис. 1. Конденсатор на произвольной поверхности

Рассмотрим вариационную задачу

I G (Vh, Vh) dM >  inf.

M ( r,R )

Известно [1, гл. 3, § 4, п. 4.1, свойство 3], что эта задача имеет решение h0(x) Е Cd(Q), такое что

cap G (P, dfi;

fi) =

I G(Vh ₀ , Vh ₀ ) dM.

M ( r,R )

Для доказательства теоремы 2 нам потребуется теорема, доказанная в работе [3].

Теорема 3. Пусть M — экстремальная поверхность для функционала (1) со знакоопределенной матрицей G. Если найдется область fi с M и компакт P ^ fi такие, что j ||A||GdM > capG(P,dfi;fi),

P то M — неустойчива.

Доказательство. Определим допустимую в вариационной задаче (5) функцию

In lx

H^{|x| )} = —Гт.

In ^R r

Тогда, применяя (2), будем иметь неравенство capG (P, Q; fi) < I G(V^, W) dM,

M ( r,R )

которое с помощью неравенства Гельдера можно переписать в виде

I G(V^, W) dM <

M ( r,R )

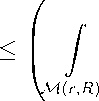
2 /n

G n/ 2(W, W) dM I

( n- 2) /n

Заметим, что в метрике поверхности выполнены следующие равенства:

VX - V (E x 2)1 / ² - 2 (E x?) ^{- 1/} 2 V (E x?) - ^2x T - X T ,

^|VI X 1 ^-

V (ln —) - ПV (1x1) - ПVM -r /     |x|       r /

Подставляя их в выражение G(V^, V^), будем иметь

1 X T

^{| x |} |x|

т x ^T №.

T TT

^G <^V^'™ ^- (^ (D ² * (й2- w) ⁺<^{Ф -}e»U) ^-

- У^ ( d ² *(t-t ) + ( ^ф - )|T| 2 ) ^XT^ -

T2

^- (^ ( D²* ⁽ T. T) ^{+ (ф -} < D*. e >» V ^- (1^2 5)2 У-^G( T, T ) <

< л(е) ।x T | 2 <  л(е) i

“ (in R)2 |x|4 “ (in R)2 |x|2 ’ где t - |XxT и использованы неравенства |xт|/|x| < 1, G(t,t) < Л(е).

Таким образом, получаем оценку емкости

< л(<)

< (in R ) ²

cap _G (P, Q; Q) <

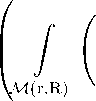
G(t,t ) |x ^T | ² (in RR ) ² |x| ⁴

2 /n

2 /n

2 / n

(n - 2) / n

<

( n- 2) /n

<

( n- 2) /n

< л(е)

< (in R ) ²

.

С учетом введенных обозначений (3) и (4) G-емкость может быть оценена следующим выражением сап                Л(^) Q2/nw(n-2)/n capG(r, Q, ^) s (in r)2 QM Vm .

Далее, применяя теорему 3, получаем требуемое.

3.    Уравнение экстремалей и вторая вариация поверхности вращения

Далее будем рассматривать функционал специального вида

F (M) = J ф(C n +1) dM,                          (6)

M где dM — элемент площади на C2-гладкой поверхности M ⊂ Rn+1, заданной радиус-вектором

RWH^W          (7)

• 6 E S ^n- 1 , p(6) — радиус-вектор сферы S ^n- 1 , t E (a,b) C R , r(t) — C ² -гладкая функция на (a, b), C n +1 — координата единичной нормали к поверхности M.

Обозначим т = £ _n +1 = — r(t)/V 1 + r ² (t) , тогда

Ф(т ) = dф/dт, ф " (т ) = d ² ф/dт ² , r = dr(t)/dt, r = d²r(t)/dt².

Пусть

B(t) = ф‘‘(т)/ ((1 + r-2(t)) ^ф(т) + ф(т)r(t)/^1 + i'2(t)^ ^ , тогда справедлива следующая теорема.

Теорема 4. Поверхность M , заданная радиус-вектором (7), является экстремальной тогда и только тогда, когда

r(t)r(t)        n — 1

-

1 + r ² (t)    B (t) + 1

Экстремальная поверхность M устойчива тогда и только тогда, когда функционал f f ht2(t,6)                 ID6h(t,6)|2 _     h2(t,6)     (n — 1)(n + B(t))

J I 1+ r ² (t) ⁽⁽⁾⁺⁾⁺     r ² (t)      r ² (t)(1 + i- ² (t))     B(t) + 1

M x (ф(т) + ф'<т)’'(«) ) dM ■ t знакоопределен в классе функций h : Rn+1 ^ R, таких, что h E C^M).

Пусть

a(t) = (ф(т) + W^ , ^r(t)    (B (t) + 1),

1 + r ² (t)) V 1 + r 2 (t)     ⁷

в п (t) =

Ф(т )r(t)

l^ф < ^{т) +} ...)

1         (n — 1) (n + B (t))

r (t) У 1 + r ² (t)      B (t) + 1

Следствие 1. Экстремальная поверхность M , заданная радиус-вектором (7), является устойчивой тогда и только тогда, когда знакоопределен функционал

/ ^{a(t) h ‘ 2 ^(t) a

— e n (t)h ² (t)} dt

в классе липшицевых функций h(t) : R ^ R , таких что h(a) = h(b) = 0.

Замечание. Теорема 4 и ее следствие 1 были опубликованы в [11].

4.    Вычисление G-емкости и ее применение для исследования поверхности вращения

Рассмотрим на поверхности M, заданной радиус-вектором (7) и являющейся экстремалью функционала типа площади (6), два замкнутых, непересекающихся множества (см. рис. 2): P = {x E M : x _{n +1} <  t 1 } и Q = {x E M : x n +1 > t ₂ }, где —то < a <  t 1 < t ₂ <  b < +то, на которых функция h(t) такая, что h| P = 0 и h| Q = 1.

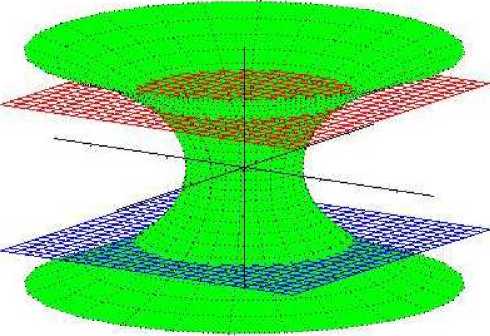
Рис. 2. Конденсатор на поверхности вращения

Пусть a(t) > 0.

Тогда G — емкость описанного выше конденсатора вычисляется по формуле capG (P,dQ;Q)

ω n- 1

t 2

/

dt a (t)

которая будет выведена в ходе доказательства следующей теоремы.

Поверхность M назовем G -параболической (см. [4]), если найдется такая последовательность подобластей 9 k С M, 9 k <е 9 _k +1 , [J 9 _k = M, что выполнено равенство k≥ 1

lim capG(P, d9k; 9k) = 0 k→∞ для любого P ⋐ M.

Теорема 5. Экстремальная поверхность M является G -параболической, если для

некоторого t0 Е (a, b)

t 0 dt = TO a ( t ) a

и b dt

J at) = ^TO t 0

причем устойчивой при P n (t) < 0 и неустойчивой при e n (t) > 0 для всех t Е (a,b).

Доказательство. Из построения конденсатора имеем, что для любой допустимой в вариационной задаче (5) функции h(t, 9) = h(t) (такое допустимо согласно следствию 1) справедливо соотношение t2

• 1    = / ⁹-М dt.

∂t t1

В силу интегральной формы неравенства Коши — Буняковского, будет верно неравенство t2

/

V a(t) dh(t)

V a(t) dt

\ 2       t 2

dt I < I a(t)h2(t) dt t1

t 2

Г dt

J a(t) '

t 1

Таким образом, t2

I ah^ (t) dt > t1

1 t ² dt t i a(t)

Интегрируя правую и левую часть неравенства по сфере Sn-1, находим t2

ah _t ² ( t ) dt d9 >

_S n - 1 t ₁

dθ

_S n - 1

t 2

Г dt

J a(t)

t 1

ω n- 1

t 2             ^,

Г dt

J a(t)

t 1

что с учетом принятых обозначений равносильно неравенству t2

I G(Vh, Vh) dM = I I a(t)h 2 (t) dt d9 >

M

_S n - 1 t ₁

ω n- 1

t 2

Г dt

J a(t)

t 1

.

Переходя здесь к точной нижней грани по всем допустимым функциям h(t) и используя равенство из определения G-емкости, приходим к соотношению capG(P,d^;^) > t^n 1 f dt

.

J a(t)

t 1

Для доказательства обратного неравенства выберем допустимую в вариационной

t 2

t 2

dt dt задаче (5) функцию h0(t) =   —— /  ——. Очевидно, что выполнено

a(t)/ J a(t)

t

t 1

t 2

cap _G (P, dQ;Q) < / I a(t)(h ₀ (t)) 2 dt d6 = t ^ n ¹

.

S n - 1 t 1                               f ^dt

J a(t) t 1

Поэтому, сопоставляя найденное соотношение с неравенством (8), будем иметь равенство capG(P, dQ; Q) = t2 n 1 .

Г dt J a(t) t 1

Далее, применяя определение G-параболичности и устремляя t1 к a и t2 к b, приходим к выводу о параболичности экстремальной поверхности вращения при условии расходимости интегралов t0

dt

= то

J a(t)

a

и b dt = то J a(t) t0

при некотором t ₀ G (a, b). Причем ее устойчивость и неустойчивость непосредственно следуют из определения.

Теорема доказана.

Пример 1. Минимальная поверхность (катеноид)

r(t, 6) = {t, ch t cos 6, ch t sin 6}, где t E (-то, +то), 6 E (0, 2п), является неустойчивой, так как функции a(t) = 1 и в(t) = —у > 0. Таким образом, заключаем, что интегралы

• 4 7     ch2t

0            0+

+∞ dt

I dt/a(t) = I dt, I dt/a(t)

-∞

-∞ расходятся и минимальная поверхность неустойчива.