Некоторые оценки непрерывного культивировании микроорганизмов

Производство биомассы микроорганизмов является основным биотехнологическим процессом. Математические модели микробиологических популяций используются в разработке технологий культивирования биомассы. Существуют несколько способов культивирования, одним из которых является непрерывное культивирование. При любом способе в культиватор помещают некоторое количество культуры – «затравку» биомассы, необходимые питательные вещества и создают необходимые температурные условия, после чего популяция развивается по своим биологическим законам. При непрерывном культивировании питательные вещества добавляются непрерывно, а часть произведенной биомассы выводится из процесса в качестве полезной продукции. Параметры технологического процесса должны обеспечивать стабильное производство.

В математических моделях непрерывного культивирования системы задается концентрацией производимой биомассы x и концентрацией субстрата S .

Объект и метод

Балансовое уравнение, описывающее концентрацию микроорганизмов, имеет вид [1] dx

— = x ( M - V ) ,            (1)

где функция µ описывает размножение популяции и может зависеть от x и концентрации субстрата S, а также от параметров среды; функция v характеризует скорость вымывания биомассы из культиватора. Рост биомассы без учёта вымывания (v = 0) задается уравнением dx

— = их.

dt

Определение явного вида функции µ(x, S) является предметом отдельных исследований. Если питательные вещества поступают в неограниченном объёме, то биомасса экспоненциально растет. Если же рост популяции чем-либо лимитирован, то величина µ будет уменьшаться. Для микробиологических популяций установлено, что функцию µ определяет концентрация субстрата S. Наиболее известной является модель, предложенная Моно, в которой предполагается, что dx µS

— = —-—x .

dt  K s + S

Формула Моно µ(x, S)= µmS/(Ks+S) позволяет учитывать насыщение скорости роста культуры при увеличения S0. Параметр µm есть максимальная скорость роста биомассы; KS – константа, равная концентрации субстрата, при которой скорость роста культуры равна половине максимальной [7–8]. Скорость роста биомассы определяется скоростью переработки питательного субстрата с помощью ферментов.

Экспериментально установлено [2–4], что скорость переработки субстрата биомассой определяется формулой Михаэлиса–Ментена:

1 dS     kE ₀ S

--—--

.

x dt К + S

m

Наиболее распространённым типом непрерывных культиваторов биомассы является так называемый хемостат, в котором скорость протока (удаления) произведенной биомассы задается технологическими условиями [5–6].

Простейшие уравнения, описывающие культивацию биомассы в хемостате, имеют следующий вид:

dx

— = м ( S ) x + D ’ ( x ) ;

• (6)

• (7)

dS dt

-a y ( S ) x - D '( S 0 - S ) ;

M ( S ) =

^ S^S K_S + S ■

Здесь S ⁰ – концентрация субстрата, поступающего в культиватор; D^' – скорость протока биомассы; коэффициент α показывает, какая часть субстрата идет на производство биомассы [7-8]. Выражение - a^(S) x описывает количество субстрата, поглощённого в единицу времени клетками культуры; величина D^'x – отток биомассы; D^'S – приток клеток культуры в культиватор; - D^'S ⁰ – отток использованного субстрата из культиватора. Скорость роста биомассы µ берется в соответствии с формулой Моно.

Результаты и обсуждение

Уравнения (5)–(7) являются базовыми в технологиях производства микробиологических культур. Введем безразмерные концентрации ax _ S x ’ y=Km ’

S ⁰

У ⁰ =7"

Km

и безразмерные время t'=tµm и скорость протока D = D'/µm и запишем систему (5)–(7) в виде dx - ц( y) X'- Dx‘; ^=-^к y)x'+D (y о- y);

д ( y ) = y- . (11) 1 + y

В практических приложениях важное значение имеют стационарные решения системы и их устойчивость.

Моделирование в системе Mathcad позволяет оценить возможность получения на практике таких режимов. На графике х (нижняя поверхность после точки равновесия) заменена на z1 , а у (верхняя поверхность) заменена на z2

D := 0.5 a := 2.0

y

f(x , y) := x-          - D - x

V 1 + y )

z ( У 1

q^(x , y) := ^- x ⁺ D - ^{(a -} y)

V 1 + y )

Given

^f(x , y) = ⁰        q^(x , y) = ⁰

q(1 , 1) = 0         f(1 , 1) = 0

V := Find(x , y)

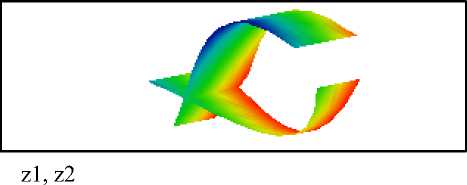
Рисунок 1. Численная оценка скорости роста дрожжей в программе Mathcad

Figure 1. Numerical evaluation of the rate of growth of yeast in the program Mathcad

Заключение

Анализ полученных численных оценок говорит о том, что традиционные кривые равновесия могут видоизменяться при «закри-тических» параметрах процесса: температуре, давлении и влажности.