Некоторые оценки основной частоты для финслеровой метрики

Пусть в области D С R n задана непрерывно дифференцируемая, неотрицательная функция Ф(х, £) , удовлетворяющая условиям:

• 1. V £ G R n , а >  0 Ф(х, а^ ) = аФ(х,^ ).

• 2.    Ф(х,£) выпукла по переменной £ .

• 3.    Для любого x G D множества S(x) = { £ G R n : Ф(х,£) <  1 } локально

равномерно ограничены.

Определим двойственную к функции Ф(х,£) функцию

H ⁽ x,n)

(С,п} sup ©,n; = sup ——-.

e e =(x)          §=0 ^{Ф( х,} £)

Ясно, что функция H (x,n) является однородной степени 1 по переменной п Введем финслерову метрику d(x, у) , полагая

d(x, у) = inf ^γ

j H (x, dx),

γ

V x, у G D,

где точная нижняя грань берется по всем локально спрямляемым кривым y G D , соединяющим точки x, y (см.: [3]). Область D с определенной так финслеровой метрикой будем называть финслеровым пространством .

Рассмотрим иллюстрирующий пример. Предположим, что в области D С R n задана положительно определенная квадратичная форма 52^=1 a ij C i C j и определим функцию Ф посредством равенства

n               \1/2

.

^{ф( x,£} ) = y^E a ij ^{( x ) £} i ^£jJ

Так определенная функция Ф(x, £) удовлетворяет условиям (1)-(3). Метрика d , заданная равенством

n

d(x, y) = inf

n

. У a ij (x)dx i dx j , Y A M=1

γ

где a ij (x) — элементы обратной матрицы к матрице \\ a ij (x) || , совпадает с обычной римановой метрикой в области D .

Пусть h(x) : D ^ R, 0 < h(x) < + то , Vh = 0 — функция исчерпания области D .

Введем множества

D(t) = { x G D : h(x) < t } , ^(t) = { x G D : h(x) = t}.

Определим основную частоту множества X(t) по формуле

АРЮ =

JE(t)

^{ф р ( х,} У _Е ^^{( х ))}

|V h(x) |    ^d H n^-1

inf

^(x) e c l (s(t)) f(_(t) y ^{p ( x ) lV h ( x ) l} d ^H n-i

,p > 1.

Заметим, что для области в R n и функции Ф(x, £) = | £ | основная частота имеет конкретный физический смысл и достаточно хорошо изучена (см., напр., работы: [1; 2; 6] и др.).

Будем рассматривать оператор

L[f] = div(A(x, V Ф2(x, Vf (x))), где A(x, £) : D х Rn ^ Rn — C 1-гладкая функция. Предположим, что

( A(x, V ^ Ф ² (х,п),П >  С 1 Ф ² (х,п),

H (x, A(x, V $ Ф ² (х, n))) <  С 2 Ф(х,п).

Условия (1)-(2) для A(x, Y ) = Y выполняются автоматически в виде равенств и с постоянными c ₁ = c ₂ = 1 .

Для получения оценки величины А ₂ воспользуемся методом, предложенным в работе Яу [6].

Теорема 1. Если f (x) — положительная C ² -гладкая функция в Q , то

A 2 (S) >  c l inf c ² 3

div( - A(x, V ^ Ф ²

(x, V f)) A

|V h |             )

lw\

.

Доказательство. Для произвольной C 1 -гладкой финитной функции u(x) по формуле Гаусса — Остроградского

0 = у div (u ²

A(x, V _s Ф ² (x, Vf )) f\Vh\

о f ю A(x, V^ Ф ² (x, Vf )). , J dx = 2 у u (V u,------ f \Vh\ ------? dx+

-

⁺ к

u ² |V h | div A^^x ^ ^f )) dx

u ² |V h | div

fiVhi

(A(x, ∇ ξ Φ ² (x, ∇ f))) |∇ h |

^^^^^^^^^r

f ₂(A(x, V Ф 2 (x, V f)), VfV

J s u -------- f 2 |V h|-------- dx ^-

f |V h |

dx + 2 ^ ^{U Ф} fxVVl h (A(x, V^2 (x, Vf )))dx-

f u ^{2 ф 2 (} x, ^Vf ))

^^^^^^^^^r

^c 1 L     f 2 iVhi    ^dx -

Добавим и вычтем интеграл вида c2 г $2(x,VM) cik   |Vh|   dx, получим

_f u ² |V h | ^di v ^A(xM ^ ; 2 h ^{(x, V f} ))       c 2 г

^{0 -} к       f |V h |        dx ⁺ cJ s

+ 2C2 /

Σ

uФ(x, V f )Ф(x, V u)

f |V h |

dx r c ₁

Σ

u ² Ф ² (x, V f ) f ² |V h |

Ф ² (x, V u)

|V h|    '

dx - c2 / c1 Σ

dx +

Ф ² (x, V u) , dx.

|V h |

Последние три слагаемых свернем в квадрат разности

u

⁰ "

Σ

2     A(x, ∇ ξ Φ ² (x, ∇ f))

' ^div         jy h j

r

f f ГuФ(x, Vf)dx Js [ Vdf|Vh|

dx + C2 [ ^{ф 2} ( x. Vu ) dx

C i 7s    |V h |

^^^^^^^^^r

r

C 2 Ф(x, V u)

dx.

Отбросим последнее слагаемое, поскольку оно всегда отрицательно.

0 - c2 [ c1 Σ

Введем величину

Ф ² (x, V u) , dx

|V h |

^- i, f ^div(

- A(x, V _s Ф ² (x, Vf )) |V h |

dx.

Тогда неравенство

A ₀ = inf

Σ

div(

A(x, V _€ Ф ² (х, У f )) )"

|∇h| f |Vh|

.

может быть записано в виде

c 2 г ^ф2 xAuax ^- ci к   |V h | ^d

r

A ₀ j u ² |V h | dx.

Следовательно, для основной частоты λ 2 справедлива оценка

A 2 (E) >  c ¹ ^ ⁰ c ₂

.

Аналог неравенства Чигера

Далее будем считать, что R ^{n +}1 D D = Q x (0, + ^ ) , h(x) = x n+1 . Тогда S(t) = Q x x { t } и

A p (Q) = inf J^pCxWfdx. ^ e c 0 (Q)    J_Q ^ p (x)dx

Введем в рассмотрение величину

^b^dx •

G⊆Ω      |G| где G-компактная подобласть области fi, а v — вектор внешней нормали к границе dG. Заметим, что h(fi) для случая Ф(x•^) = |£| была введена Чигером в работе [5]. Обозначим также fit = {x G fi : f (x) > t}, Et = {x G fi : f (x) = t}.

Теорема 2. Имеет место оценка

A p (fi) >  P p h ^p (fi).

Доказательство. Пусть f (x) — функция, на которой достигается точная нижняя грань в определении λp, то есть х = /п ФР(x, у/)dx • (/n fp(x)dx)p/q > (/n Ф^ у/) • fp/q(x)dx)p p      In fp(x)dx     (Ja /p(x)dx)p/q          (Jn fp(x)dx)p       '

Здесь мы воспользовались неравенством Гельдера

(^ Ф(x• У/) • fp/q(x)dx^P < j Фp(x• У/)dx • (J fp(x)dx^P/q и соотношением 1 + p/q = 1. По формуле коплощади [4]

λ p ≥

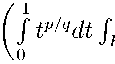
.t ^ф(f dH n -?j Р    Q t pq dt J_{E t} Ф(x•vJdH n -^ P

(J^fp(x)dx)p hp(fi) Q tp/q |fit |dt)

>      ⁽ J q ^{f p ( x ) dx )} p

(J ^ ^{f p ( x ) dx}) p

p

,

≥

поскольку в силу определения величины h(fi) выполнено | fi t |- h(fi) <  У Ф(x•v)dH n - i .

Проинтегрируем по частям интеграл, заметив, что | fi 1 1 = 0 :

t> /q \fiAdt = 1 jwp = - 1 jt p >|dt. 0  00

Так как

/ dT L, iyf(x)TdHn-1) = - Ie, |yT(x)idHn тогда hpW pp (f tpdt fEt |Vf(x)| dHn-1^

AP > —TT^0-----------= p;p hp №• f tpdt JEtt I^f (x)| dHn-1j

К интегралу в знаменателе снова была применена формула коплощади

Окончательно

/

J Q

• f p (x)dx = I t p dt I ¹   dH n - i .

E t |V ^{f ( x ) |}

A p >  -1 h ^p (0).

p ^p