Некоторые основные параметры косозубого ступенчатого долбяка

Во всех применяемых способах зубоформирования размеры инструмента в какой-то степени передаются на обрабатываемую поверхность в зависимости от кинематики зубона-резания. Поэтому точность зубоформирования в значительной степени зависит от точности параметров формирующего инструмента [1-4].

Процесс скоростного зубодолбления косозубым ступенчатым долбяком новый [5, 6]. Процесс не освоен, и не выявлены конструктивные и технологические связи между элементами технологической системы. Поэтому выявление связей между конструктивными элементами ступенчатого долбяка и кинематикой зубоформирования при зубонарезании является актуальной задачей.

Целью работы является определение некоторых основных параметров ступенчатого долбяка на основе действующих размерных связей: инструмент обработанная поверхность.

Для достижения поставленной цели составляются схемы геометрических связей между выбранными параметрами ступенчатого долбяка и формируемыми ими параметрами обработанной поверхности и решается соответствующая размерная цепь.

Диаметральные размеры зубчатых поверхностей формируются в основном наладочным размером [2-5]. Профиль, толщина зубьев и т.п. формируются размерами инструмента в сочетании с их многочисленными положениями, обеспечиваемыми «жестким» (по сравнению с наладочным размером) приводом оборудования. То есть эти параметры нарезанных зубьев формируются суммарными размерами элементов технологической системы (в дальнейшем, размер системы). При этом размер инструмента является основной частью размера системы.

Выявление связей, действующих между размерами нарезанных зубьев и инструментом, и их учет в конструкции долбяка позволяют достигнуть наибольшей точности обработки при выполнении операции.

Определение некоторых основных параметров долбяка

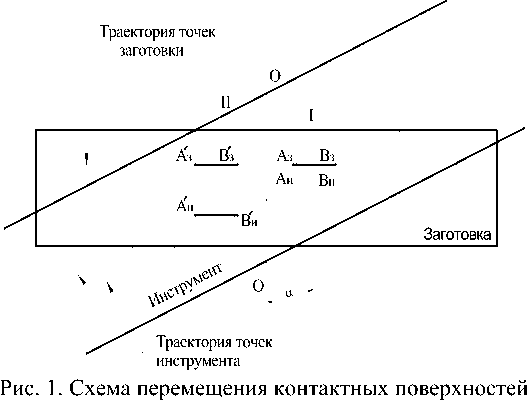
Делительный диаметр. Одним из основных расчетных параметров зуборезных долбя-ков является диаметр делительной окружности на исходном контуре. Нарезание зубчатых поверхностей специальным долбяком осуществляется при скрещивании осей заготовки и инструмента при непрерывном вращении последних вокруг собственных осей. Контактирующие точки режущих лезвий инструмента и заготовки вращаются в плоскостях, пересекающихся под углом ОС (рис. 1). Для обеспечения параллельности образующих нарезанных зубьев оси колеса необходимо, чтобы контактирующие в положении I точки инструмента АиВи и заготовки А3В3 при некотором их согласованном повороте в положение II располагались на прямых, параллельных оси колеса (А'зА'и || ОО; В'зВ' || ОО). Это условие обеспечивается при равенстве проекций скоростей вращения точек инструмента и заготовки на плос- кость, перпендикулярную к оси заготовки, т.е.

V з =V и cos ОС ,                                        (1)

где Vз и Vи  скорости вращения точек заготовки и инструмента, расположенных на соответ ствующих делительных окружностях; ос - угол скрещивания осей заготовки и инструмента.

При нарезании зубьев методом огибания условие (1) может быть обеспечено при диаметре делительной окружности на исходном контуре инструмента ( Dди )*

DДИ m zИ cosа где Zи число зубьев инструмента; m модуль нарезаемых зубьев.

долбяк – заготовка

Технологическое обеспечение D ди должно осуществляться за счет положительного коррегирования при изготовлении инструмента. Величина коррекции определяется формулой:

1 m m z_И

2 cos а

m zИ

m zИ

1     1.

cos а

Эксперименты, проведенные на машиностроительном заводе им. Г. Мусабекова при mz нарезании зубьев ступенчатым долбяком с D       И , подтвердили вышеуказанные тео- cosа ретические предположения.

Модуль . Как показано на рисунке 1, шаги нарезаемых зубьев и зубьев инструментов в нормальном сечении равны. Поэтому нормальный модуль инструмента m n =m. Тангенциальный модуль инструмента m и определяется с использованием связи:

D = z

ДИ   z _И

m

mzm

। — И И         ; mИ cosос        cosОС

.

Число зубьев инструмента. При нарезании зубьев косозубым ступенчатым долбяком профиль формируется определенными положениями разных зубьев инструмента.

Гладкость эвольвентного профиля зависит от количества режущих зубьев, формирующих зуб детали. Чем больше зубьев инстумента участвуют в формировании профиля, тем качественнее он обрабатывается. Это обеспечивается оптимальным решением проблемы высоты охвата зубьев и диаметра инструмента. При калибровке все зубья инструмента участвуют в формировании каждого зуба.

Задный угол. При обработке металлов резанием особое значение имеют геометрические параметры режущих инструментов. Одной из особенностей процесса нарезания зубьев ступенчатым долбяком является то, что при формообразовании значения фактических геометрических параметров (передний, задний и другие углы) изменяются в каждый момент резания. Поэтому для выбора оптимальных значений геометрических параметров, свойственных данному условию резания, необходимо иметь и представление о закономерности их форми- рования в зависимости от кинематики резания.

Задний угол инструмента играет немаловажную роль в процессе резания и в обеспечении качества обработанной поверхности. Поэтому здесь исследуются связи между задним углом на вершинах зубьев ступенчатого долбяка ОС з и кинематикой нарезания при формировании внутренних зубьев.

Допустим, что задняя поверхность на вершине зуба долбяка образует угол р на осевой плоскости, проходящей через серединную точку вершины А (рис. 2). При этом линия AN является линией пересечения задней поверхности с осевой плоскостью инструмента. Однако задний угол на вершине зуба при резании формируется на осевой сечении заготовки в направлении резания, т.е. ОС з =ZQAM. Одна из сторон заднего угла AM должна находиться на задней поверхности. Так как режущее лезвие BC и линия AN принадлежат задней поверхности, значит, линия BN также принадлежит задней поверхности. Из геометрических построений и связей:

ZNAO =Р;  AON=90°;

z QAM=zAMO=а з ; ZBAN=90°; ZAOН=90°;

AK||EO; AK=EO; ZBON=90°;  KO=AE из АAMK и АЕАО

AK EO tg а                ;

З KM KM

EO r2  r2 sin2   cos2    r 1 sin2   cos2 , где r1  наружный радиус режущих зубьев долбяка; Ф - искомый угол поворота режущего зуба от выбранного начала отсчета.

Для упрощения обозначим:

BM=b; MN=d; MO=f; лNBO=V;ZBNO= из А MON и А BON. Согласно теореме синусов df sin sin ;

f sin а d             ;

sin у

bffcosа ; b sin(90o -а)  sin^        sin

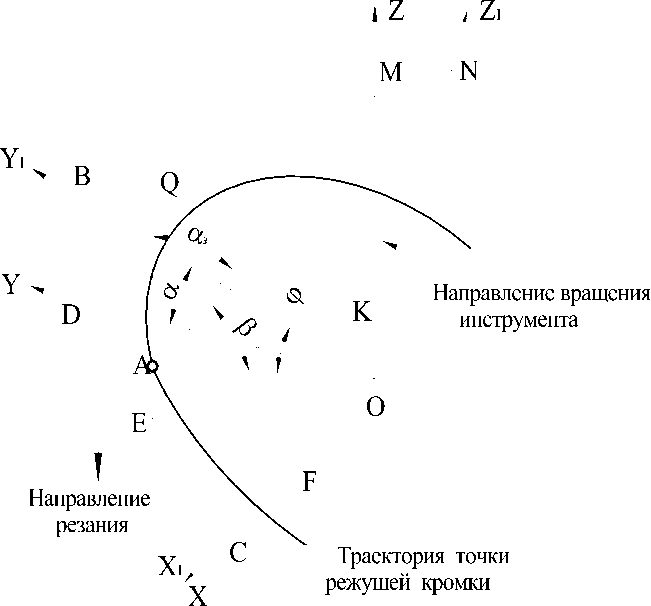
Рис. 2. Схема формирования заднего угла ступенчатого долбяка при нарезании внутренних зубьев

Для определения уиV определяем отрезки BO и NO. Из А BAO и А ANO:

AO           AOr cosф; BO            x ;(9)

BO            cosфcos^

NO tg р; NO AOtgр=r1 tg р .(10)

AO

Из \ BON

BN =VBO2 + NO2    r1    1 + cos2 ф- tg2р;(11)

cos2 ф или

NO     cos ф- tg р           BO        1

, sin г=—=            ;

BN   V1+ cos2 ф-tg2 р        BN 1+ cos2 ф-tg2

Сложим выражения (7) и (8)

^f sin аf cos а d+ b BN

sin у

sin^

r ₁   ,     22        f sin а

11+ cos 2 ф- tg2           f s n cos ф                             1

f cos а cos Ф* tg р

1 + cos² ф"tg ² р    ^1 cos² ф- tg ²

Разделим каждую сторону равенства на   1 + cos ² ф' tg ² р и определяем f.

.

f

r ₁ tg р

cos а + sin а- cos ф-tg ^,

тогда r tg в                .

KM f AE          ^{r 1 tg}           r sin ос- cos ср

.

cos а + sin а- cos Ф*tg    ¹

Учитывая выражения (6) и (16) в (5) и проведя у прощения, получим:

1 sin² а- cos² Ф * (cos ОС* sin а- cos Ф*tg Р ) з   _tg Р - sin а- cos Ф* (cosа + sin а- cos Ф*tgР )

Выражение (17) удобно для решения обратной задачи. То есть на основе выбранного значения заднего угла определить конструктивный параметр долбяка угол р.

Последнее выражение есть математическая модель кинематического заднего угла на вершине зуба долбяка. Применяя ее и используя диапазон изменений угла поворота ф в пределе съема материала (ф min <ф<ф_max, где ф min и ф max углы, соответствующие началу и концу съема материала), определяем и принимаем значение заднего угла долбяка.

Высота охвата режущих зубьев 2Н. Режущие лезвия косозубого долбяка на определенном уровне расположены ступенчато. Минимальная высота охвата режущих частей зубьев 2Н определяется длиной нарезаемых зубьев и углом наклона оси долбяка. Увеличение высоты охвата зубьев 2Н по сравнению с требуемым обусловливает появление нерабочих зубьев инструмента и снижает эффективность обработки.

Определение высоты охвата зубьев инструмента рассмотрено на примере нарезания наружных цилиндрических зубьев с учетом того, что крайние точки станочного зацепления формируются наружными диаметрами заготовки и инструмента.

Из-за скрещивания осей инструмента и заготовки начальная точка А и конечная А 1 станочного зацепления смещаются вдоль образующей нарезаемого зуба (рис. 3). Лимитирующими являются зацепления на торцевых поверхностях венца заготовки. При этом крайние точки станочного зацепления в одной и той же плоскости, перпендикулярной к оси заготовки, имеют место на разных зубьях инструмента. На рисунке 3 представлена схема образования верхних крайних точек (А и А 1 ) станочного зацепления на торцевой поверхности при нарезании наружных зубьев. Положение точки А определяется пространственной размерной цепью.

OB + BA + AE + EC + CO 0, (18) где ВА наружный радиус режущих зубьев долбяка, r 1 ; АЕ наружный радиус зубчатого колеса, R 1 ; ЕС кратчайшее межосевое расстояние инструмент заготовка, a ; СО половина длины нарезаемых зубьев, l ; ОВ половина высоты охвата ступенчатых зубьев инструмента, H .

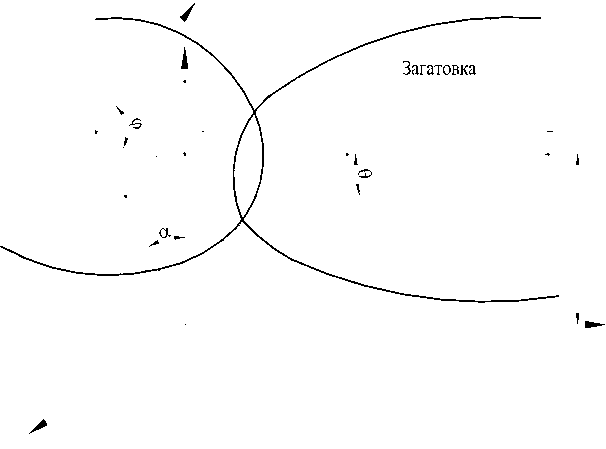
Рис. 3. К определению высоты охвата зубьев инструмента при нарезании наружных зубьев

Согласно условиям обработки:

BA r  mИ zИ ч hИ ; AE R  mzч ha ; EC a  mИ zИ + mz

1        2         И;            1     2      a;                        2         , где hи и hа  высота делительной головки зубьев инструмента и колеса; z число зубьев на- резаемого колеса.

В пространственной размерной цепи (18) неизвестными являются направления составляющих звеньев ВА и АЕ и величина ВО. Сущность ее решения заключается в том, чтобы найти такое значение Н , при котором обеспечивается замкнутость цепи с заданными значениями составляющих звеньев. Приняв направления радиус-векторов ВА и АЕ соответствующими некоторым углам фи о (углы поворотов «контактирующих» точек зуба инструмента (режущая точка) и заготовки, рис. 3), найдем проекцию составляющих звеньев размерной цепи на оси Z и У координатной системы ОХУZ.

Y H sin а + r cos 6* cos а - R sin Ф =0 i 1                                              1

Zl+ r cos 6- sin а- H cos а =0 i 1

Решив последнее системное уравнение, находим:

H l cosа sin Ф =             .

r sin а

Расчленив размерную цепь (18) на две составляющие цепи

OA OB + BA и AO OC + CE + AE и учитывая, что они имеют общее замыкающее звено, получим:

OB + BA OC + CE + AE

или

Отсюда

H ² + r ² l ² + ( a R cos ср )² + R ² sin² ф

H ² + r ²   l ² + a ² 2 aR cos ф^R ² cos ² ф^ R ² sin ² ;

cos ф =

l ² + a ² R ² H ²   r ²

2 aR

Возведя в квадрат выражения (21) и (25), суммируя их и учитывая, что (соs2ф + sin2ф) = 1, получим:

l ² + a ² R ² H ² r ² "  H l cos а? ²

• 11- + ---

• 2aR        J ( r sinа )

Уравнение (26) содержит одно неизвестное Н , которое необходимо определить. Однако традиционными математическими методами определить Н из (26) нерационально. Уравнение (26) решается методом последовательного деления отрезка пополам. Составлены алгоритм ее решения на ЭВМ и программа для вычисления H .

Решение уравнения (26) дает две пары значений, соответствующие точкам А и А 1 .

При нарезании внутренних зубчатых поверхностей формирование конечных точек станочного зацепления аналогично нарезанию наружных зубьев. Соответственно, при этом Н определяется аналогичным образом.

Высота охвата ступенчатых зубьев инструмента 2Н один из важных параметров при проектировании режущего инструмента. Зная 2Н , можно определить число одновременно работающих режущих зубьев, число режущих зубьев, формирующих каждый нарезаемый зуб, влияющие на процесс нарезания зубьев колес специальным долбяком.

Выводы

• 1.    Определены некоторые основные параметры косозубого ступенчатого долбяка: модуль, диаметр делительного диаметра на исходном контуре, величина коррегирования.

• 2.    Выведена математическая модель кинематического заднего угла на вершинах зубьев.

• 3.    Выведена математическая модель для определения высоты охвата зубьев.