Некоторые особенности накопления задержек при передаче пакетов по сети с кольцевой топологией

где l – номер узла, которому адресован рассматриваемый пакет; 1% – общее число узлов сети; M^M^M^MJ – план распределения информации на сети; М; _ч) – маршрутная таблица i – узла; ^rt – ранг узла i ; P ^— [Aj ^_м+1)х(и_м+1) ^— матрица переходных вероятностей, описывающая процесс передачи пакета по сети при поиске искомого узла / ;

N ^— \_^ki ](и_ы-1)х(и_м-1) – фундаментальная матрица; л ^— t^/Lx/i – матрица интенсивностей поступления пакетов; ^ ^k^x« – матрица вероятностей блокировок ветвей сети; - V^ij Anxn – матрица суммарных интенсивностей поступивших потоков на ветви сети и адресованных всем узлам сети. Ее элементы рассчитываются по формуле:

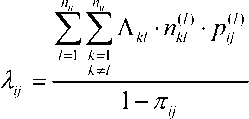
где 2Q – начальные значения потоков на ветвях сети.

После определения потоков в стационарном режиме вероятности потерь пакетов рассчитываются по формуле B^w = N^w -R^m . Они содержатся во втором вектор столбце матрицы в , где R^ ^ [^ij ^}](„ -l)x2 – матрица вероятностей перехода из невозвратных состояний в поглощающие; B^ ^ №j ^(и -l)x2 – матрица вероятностей достижения поглощающих состояний.

Задержки доставки пакетов будут равны:

где t =№^uL„-i - вектор задержек доставки пакетов; V^ij An xn – матрица задержек в передаче пакетов по ветвям сети; – модифицированная фундаментальная матрица.

Для анализа нам потребуется также расчет таких показателей, как очереди и уровни загрузок каналов сети. Обозначим через ^Cy пропускную способность канала, соответствующего ветви ( ij ), через ^Oij ^{И W}ij – очередь и число мест ожидания, через Ц – величину, обратную длине пакета. Ранее были обозначены через Ту И Лу – задержка при передаче пакета по ветви Qu3 и вероятность ее блокировки, через ^u – поток, поступающий на ветвь Qu3 .

Указанные величины связаны между собой следующим образом [5]:

Py=fM’cu’^; Oy=fo(ky,Cy,B);

Tv=H^,Cy,B); ^=fA^y^y,Wy,^.

Ниже рассмотрено применение модели на конкретных примерах, при подборе которых была учтена архитектура сети, ориентированная на оказание перспективных услуг связи. Ее характерной особенностью является наличие единой точки предоставления услуг. Это означает, что весь трафик должен проходить через единое устройство, которое обычно называют сервисным маршрутизатором, а сам характер тяготения при этом становится централизованным.

Накопление задержек при передаче пакета по магистрали сети с кольцевой топологией

На рис. 1 приведен пример сети с кольцевой топологией, содержащей 8 узлов. Рассмотрим накопление задержек при передаче пакетов между центральным магистральным узлом (ЦМУ) и всеми остальными магистральными узлами (МУ) сети.

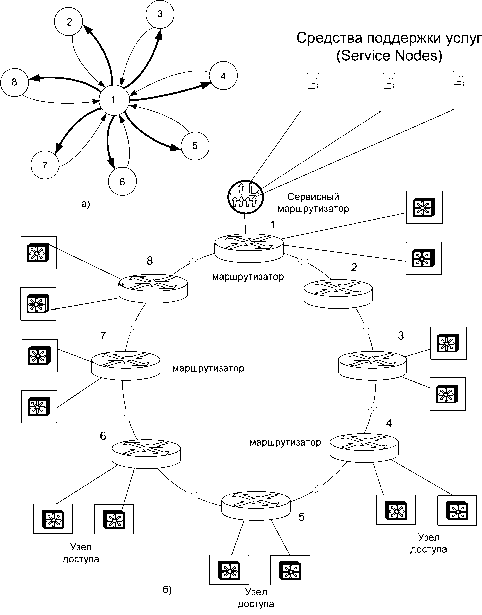
Рис. 1. Пример построения магистрали транспортной сети с кольцевой топологией: а) – структура тяготения; б) – топология сети

При расчете приняты следующие исходные данные:

• -    топология – кольцевая;

• -    число узлов – 8;

• -    характер тяготения – централизованный;

• -    число центров тяготения – 1, номер ЦМУ – 1;

• -    число классов обслуживания – 1;

• -    тип системы СМО, описывающей СБК, – M/M/1/N;

• -    длина пакета /^=1,5-10⁴ бит;

• -    число вариантов расчета – 2:

• -    вариант 1: пропускная способность каналов на каждом участке C = 10 Мбит/С; интенсивности поступления пакетов между ЦМУ и каждым МУ принимают следующие значения 2 = 5-10* , 2 = 10-10* , 2 = 15-10* пак/С;

• -    вариант 2: пропускная способность каналов на каждом участке C = 10 Мбит/С; пропускная способность ветвей (1-2) и (1-8) удвоена; интенсивность поступления пакетов между ЦМУ и каждым МУ составляет 2 = 15-10* пак/С;

• -    число буферов на каждое направление со = 10.

Результаты расчета:

• -    распределение потоков, уровней загрузок, очередей для 3 значений нагрузки. Накопление задержек при передаче пакета по магистрали сети для варианта 1 (см. рис. 2);

• -    распределение потоков, уровней загрузок, очередей. Накопление задержек при передаче пакета по магистрали транспортной сети для варианта 2 (см. рис. 3).

  
  
  
  
  
  
  

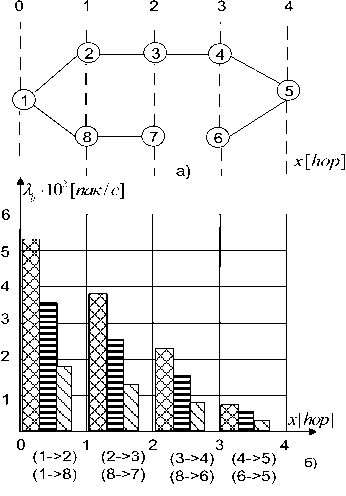
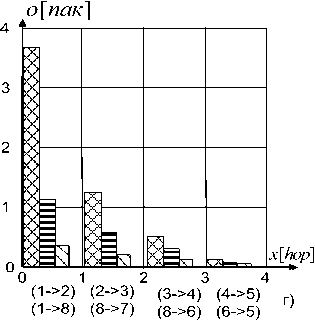
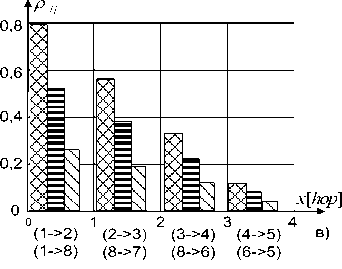
  И ^^IS-l^^/c] g ^^lO-ld^/c]

  Рис.2. Накопление задержек при передаче пакета по магистрали транспортной сети при трех значениях нагрузки

  
  
  

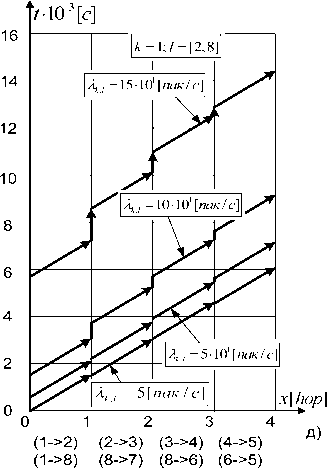
  □ ^ = 5 • 1О¹ \naid с\

  
  

На рис.2а показана топология сети, содержащей 8 узлов, а на рис. 2б-д, соответственно, величины потоков, поступающих на ветви сети, уровни загрузок каналов, очереди, а также график, иллюстрирующий процесс накопления задержек при передаче нисходящего потока между ЦМУ и всеми МУ. На осях абсцисс рис. 2 указано расстояние между ЦМУ и МУ в числе переприемов (хопах); отмечены также ветви, соединяющие соседние узлы. Так, например, узлы 2 и 8 удалены от узла 1 на расстояние 1 переприем. Узел 1 соединен с узлом 2 при помощи ветви (1->-2), а с узлом 8 – ветвью (1->-8).

Для рассматриваемого примера интенсивности л._ы (для нисходящего потока) равны 15-IO¹; 10-Ю¹ и 5-10* пак/С, а интенсивности Л (для восходящего потока) приняты равными 3-10*; 2-10* и 1-10 пак/С. Эти интенсивности соответствуют режимам большой, средней и малой нагрузки. Д ля рассматриваемого случая к = 1, а / е [2,8]. Как следует из графиков, изображенных на рис. 2б-в, наибольшая нагрузка поступает на вет-

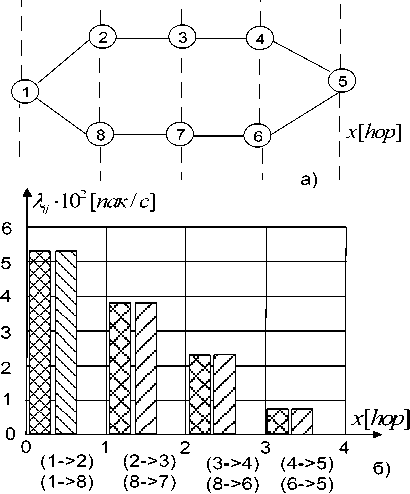
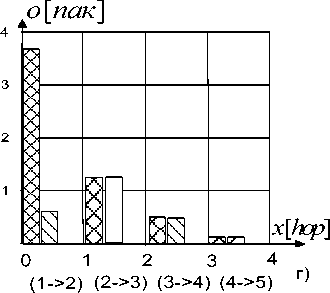
(1->8) (8->7) (8->6) (6->5)

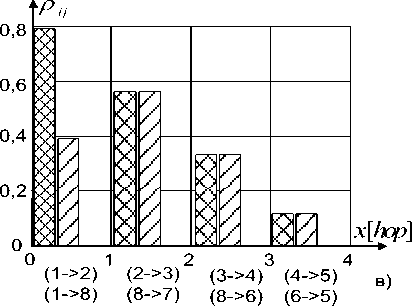
(1->8) (8->7) (8->6) (6->5)

® Пропускная способность всех каналов равна \ б Мбит i с

Q Пронусная способность с, ₂ = с^, = с₈, = q,, —20 Мбнт^ с, остальных каналов — 10 Кбит! с

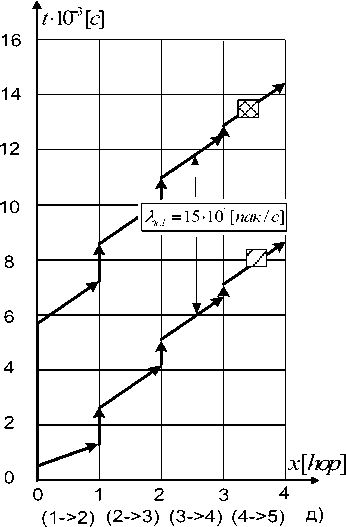
Рис. 3. Результаты исследования влияния увеличения пропускной способности канала на самом перегруженном участке сети ви (1->-2) и (1->-8), а наименьшая – на ветви (4->-5) и (6->-5). Рис. 2д иллюстрирует накопление задержек при передаче пакета по ветвям сети, которая для каждой конкретной ветви складывается из двух составляющих: времени ожидания в очереди и времени передачи по каналу.

При этом (см. 2д) вторая составляющая является постоянной и равна частному от деления размера пакета на скорость передачи по каналу, а первая определяется уровнем загрузки канала. Наибольшие очереди пакетов скапливаются на направлениях (1->-2) и (1->-8), а наименьшие – на (4->-5) и (6->-5). Это понятно, поскольку именно эти ветви характеризуются наибольшей степенью нагрузки. По мере удаления от ЦМУ очереди «рассасываются» и вклад удаленных от ЦМУ ветвей в общую задержку сокращается.

Выше было отмечено, что наибольшие очереди пакетов, а следовательно, и задержки имеют место на направлениях (1->-2) и (1->-8). Поэтому естественным предложением сокращения задержек является увеличение пропускной способности именно на этих участках. Такое увеличение может быть осуществлено путем организации дополнительного физического канала с последующим объединением его с уже существующим каналом в единый логический канал. Возможен также переход на предусмотренную стандартом новую скорость передачи.

Оценим эффект от увеличения скорости на участках (1->-2) и (1->-8) в 2 раза (см. рис. 3) . Заметим, что поскольку канал является дуплексным, то удвоятся также и скорости передачи на участках (2->-1) и (8->-1). Удвоение скорости привело к тому, что уровень загрузок наиболее загруженных участков умень- шился с 0,790 до 0,395, что привело к уменьшению очередей на этих направлениях с 3,76 до 0,649 пакетов. Столь существенное сокращение очереди уменьшило время передачи пакетов между ЦМУ 1 и МУ 2 с 7,14-Ю"2 С до 1,12-10 С, что, в свою очередь, привело к сокращению задержек между ЦМУ 1 и всеми другими узлами сети. Обратим внимание также на то, что после удвоения пропускной способности на участках (1->-2) и (1->-8) наиболее загруженными стали ветви (2->-3) и (8->-7). Уровень их загрузки составляет 0,553, а размер очереди – 1,24.