Некоторые особенности получения изображения в компьютерном рентгеновском томографе

Визуализация внутренних органов представляет собой важнейшую цель многих методов диагностики. Визуализация с помощью рентгеновской томографии явилась существенным прорывом в диагностике, использующей рентгеновское излучение. Рентгеновскую томографию предложили английские физики А. Кормак и Г. Хаунс-филд, за что в 1979 г. им была присуждена Нобелевская премия.

Принцип линейной рентгеновской томографии в его первоначальном виде показан на рис. 1. Источник рентгеновских веерообразных лучей 1 (веер перпендикулярен плоскости рисунка) совершает качания, так что лучи проходят через центр качания 3 , находящийся в теле пациента 2 . В дальнейшем лучи попадают на фотопластинку 4 , которая также совершает качания в такт источнику излучения 1 . На пластинке получается изображение небольшой области вблизи центра качания 3 , а более удаленные области оказываются на пластинке смазанными, т. к. через них лучи проходят периодически. По этой

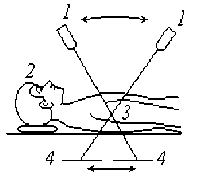
Рис. 1. Принцип линейной рентгеновской томографии же причине, окружающие центр качания небольшие непрозрачные включения, не мешают получению изображения. Если изменять положение центра качания, например, послойно, то можно получить хорошее изображение патологического очага.

В настоящее время наиболее распространенным вариантом рентгеновской томографии является компьютерная рентгеновская томография (КРТ или КТ). В компьютерном рентгеновском томографе, рис. 2, пациент 1 помещается в сканирующее устройство 2 , вращающееся вокруг исследуемого объекта. Рентгеновские лучи от излучателя 3 расходящимся тонким (1–10 мм) веерным пучком проходят через пациента, лежащего на кушетке и попадают на детектор 4 , представляющий собой матрицу из 500 ^ 1000 фотоэлементов или ионизационных камер.

В случае, показанном на рис. 2, в процессе вращения сканирующего устройства 2 , компьютер 5 анализирует прохождение лучей в сечении по разным направлениям и на основе этого строит изображение всего сечения. Возможность и способ такого построения показал немецкий математик И. Радон в 1917 г. [1].

Затем пациент перемещается вдоль оси томографа, и процедура получения изображения повторяется снова для следующего слоя исследуемого органа. Предел разрешения компьютерного томографа до 2 мм при различии в коэффициенте поглощения рентгеновского излучения для веществ ~ 0,1 %. Например, с помощью компью- © Волобуев А.Н., Адыширин-заде К.А., Антипова Т.А., 2017

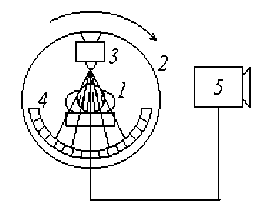
Рис. 2. Принцип современной рентгеновской компьютерной томографии

терного томографа можно различить серое и белое вещество мозга.

1. Закон ослабления рентгеновского излучения при прохождении через вещество

Рентгеновское излучение, как и любое электромагнитное излучение, ослабляется (поглощается и рассеивается) в веществе по закону Бугера [2].

Если интенсивность излучения, падающего на вещество равна I ₀ , то интенсивность излучения, вышедшего из слоя толщиной d , равна:

I = I 0 e ^{- ц} d ,                                              (1)

где ц — линейный коэффициент ослабления излучения. С физической точки зрения он состоит из трех слагаемых:

^ц = ^ц к ^{+ ц} ф ^{+ ц} к / э ,                                ⁽²⁾

где величина ц к — соответствует когерентному рассеянию; ц ф — фотоэффекту; ц к / _э — комптон-эффекту.

Центральную роль в наблюдении органов и тканей с помощью рентгеновских лучей играет различие в поглощении этих лучей разными участками тела, органами и тканями.

Линейный коэффициент ослабления рентгеновского излучения в веществе ц в медицине часто представляют в виде двух слагаемых [3]:

ц = т + 5 ,                                            (3)

где т - слагаемое, обусловленное истинным поглощением электромагнитного рентгеновского излучения (поглощение наблюдается в явлениях фотоэффекта и частично комптон-эффекта); 5 - слагаемое, обусловленное рассеянием рентгеновского излучения (это явления когерентного рассеяния и частично комптон-эффекта).

Опыт показывает, что спектральную зависимость т в области рентгеновского диапазона длин волн для тканей организма можно представить в виде [3]:

т = k рХ 4 Z ³ , (4) где k - коэффициент пропорциональности; X -длина волны рентгеновского излучения; р -плотность вещества, подвергаемого рентгеновскому облучению; Z - его атомный номер.

Из формулы следует, что мягкое рентгеновское излучение X > 0, 01 нм, имеющее более длинные волны, поглощается сильнее, чем жесткое X < 0,01 нм. Оно более опасно для организма.

Для костей, существенную составляющую которых представляет фосфорнокислый кальций, Z = 15-20. В кости входят такие элементы, как фосфор P ₁ ³ ₅ ¹ , кальций Ca ₂ ⁴ ₀ ⁰ . Для мягких тканей Z обычно до 8. В основном это такие атомы мягких тканей, как H ¹ ₁ , C ¹ ₆ ² , N ¹ ₇ ⁴ , O ¹ ₈ ⁶ .

Если проанализировать различие линейных коэффициентов ослабления рентгеновского излучения ц для костей и для мягких тканей, то можно заметить, что слагаемое т для костей много больше т для мягких тканей, т. к. р Z ³ для костей много больше р Z ³ для мягких тканей. При этом основную роль в разнице т, а, следовательно, и ц играет различие атомных номеров элементов Z . Следовательно, кости поглощают рентгеновское излучение значительно сильнее, чем мягкие ткани. Поэтому получение контрастного рентгеновского изображения костной ткани не является сложной задачей.

Различие в ослаблении рентгеновского излучения мягкими тканями осуществляется за счет небольшого различия их плотностей р. Поэтому контрастность органов из мягких тканей значительно хуже, чем костей.

2. Математические основы компьютерной рентгеновской томографии. Преобразование Радона

Запишем Фурье-образ для некоторой замкнутой функции на плоскости от радиуса-вектора f ( r ) , рис. 3:

да

F ( k ) = i f f ( r ) 2n

-да

e

-

i kr

d r =

да

= -     f ( r ) e - ^ikr cos ⁶ d r ,

2n

-да

где k – векторный аргумент Фурье-образа или вектор волнового числа.

Угол 6 — это угол между векторным аргументом Фурье-образа k и радиусом вектором r .

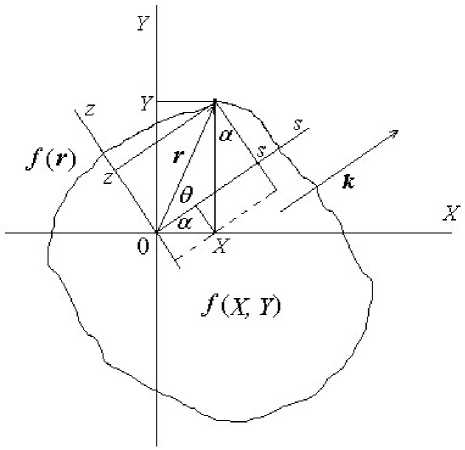
Рис. 3. К выводу преобразования Радона

F ( k cos а, k sin а ) =

да / да

=            f ( s cos а - z sin а,

2n   (

-да -да

s sin а + z cos а) dz I e

Обозначая

R (s, а) =

-

iks ds .

да

= J f ( s cos а - z sin а, s sin а + z cos а ) dz ,

-да

получаем:

да

F ( k cos а, k sin а ) =        R ( s , а ) e~^iksds .

2n

-да

Используя формулу (5), запишем двумерное преобразование Фурье для области, ограниченной функцией f ( r ) , т. е. для области f ( X , Y ) , рис. 3:

F (kX, kY ) =

да

да

= — f ( X , Y ) e i ^{( k} X ^{X + k} Y ^Y ) dXdY , 2n

-да

-да

где k_X , k_Y – проекции вектора k на оси координат X и Y .

Осуществим поворот осей координат на угол а. При этом угол а между прежней координатой Х и новой координатой s выберем таким, что координата s параллельна вектору k . Соотношение прежних координат X , Y и новых координат s , z имеет вид, рис. 3:

Формула (13) называется преобразованием Радона от функции f ( X , Y ) . Равенство (14) представляет собой Фурье-образ функции R ( s , а ) в системе координат s , z .

Таким образом, вводя преобразование Радона (13), мы переходим от двумерного преобразования Фурье (6) функции f ( X , Y ) к одномерному преобразованию Фурье (14) функции R ( s , а ) , т. е. фактически находим одномерную проекцию двумерного преобразования Фурье. Проектирование, согласно (14), осуществляется на коор-

s = X cos а + Y sin а,

динатную ось s , т. е. в направлении оси z .

Для практического применения преобразования Радона надо знать его обратное преобразование. Для нахождения обратного преобразования Радона будем исходить из обратного двумерного преобразования Фурье, соответствующего прямому преобразованию Фурье (6):

f (X, Y ) =

z = - X sin а + Y cos а.

да

да

Обратное соотношение следует из (7) и (8):

X = s cos а- z sin а ,                          (9)

= —       F ( k_X , k_Y ) e i ^{( k} X ^{X + k} Y ^Y ) dk_Xdk_Y .

2n

-да

-да

Y = s sin а + z cos а.

Перейдемв(6)ккоординатам Y = s sin а + z cos а. Учитывая k x = k cos а и k Y = k sin а, а также равенство элементов площади в координатах X , Y и s , z (площадь при повороте осей на любой угол не меняется), т. е. dXdY = dsdz , имеем:

да да

F ( k cos а, k sin а ) =          f ( s cos а

2п

-да -да

-

Учитывая, что прямое преобразование Радона R ( s , а ) зависит не только от линейной координаты s , но и от угловой координаты а, в обратном преобразовании Радона должны также использоваться только эти две координаты. Таким образом, нужно перейти к полярным координатам. В полярных координатах dk X dk Y = kdkd а.

Следовательно, обратное преобразование Фурье (15) имеет вид:

- z sin а, s sin а + z cos а) x

- ik ( X cos а+ Y sin а ) x e                  dsdz .

да 2п f (X, Y)=        F (k cos а, k sin а) x

2п

Формулу (11) можно переписать в виде:

ik ( X cos а+ Y sin а )

x e               kdkd а.

Обозначим Фурье-образ преобразования (14) в виде:

RR (k, a) = F (k cos a, k sin a) = да

= R ( s , a ) e~iks ds .

2n

-да

Следовательно, формулу (16) можно представить в виде:

f (X, Y ) = да 2n

1 в         ik ( X cos a+ Y sin a )                ⁽¹⁸⁾

= — I I R ( k , a ) e               kdkd a.

0 0

Формулу (18) можно рассматривать как обратное преобразование Радона и использовать ее для восстановления функции f ( X , Y ) по Фурье-образу RR ( k , a ) .

• 3.    Восстановление изображения с использованием преобразования Радона

Рассмотрим следующую модельную задачу. В организме, который помещен в компьютерный рентгеновский томограф, рис. 2, имеется патологический очаг – область с повышенным поглощением рентгеновского излучения. Рассеянием рентгеновского излучения пренебрегаем. В этом случае линейный коэффициент ослабления рентгеновского излучения ц = т см. формулу (3). Очевидно, при решении практических задач данное приближение неприемлемо.

Патологический очаг облучается рентгеновским излучением с начальной интенсивностью I ₀ в направлении оси z , рис. 4.

Так как линейный коэффициент поглощения может иметь различное значение в различных частях патологического очага, закон Бугера (1) нужно записать в виде:

⁺ z о

• - I ц ( X , Y ) dz

I = 1 0 e - z ⁰             .                                    (19)

Поглощение вне патологического очага используем в качестве базы отсчета и не рассматриваем.

Показатель в законе Бугера (без знака минус) будем называть рентгено-оптической плотностью патологического очага:

^{+ z} 0

D = J ц ( X , Y ) dz .                            (20)

• - z ₀

Формулу (20) можно рассматривать, как преобразование Радона от функции ц ( X , Y ) . Преоб-

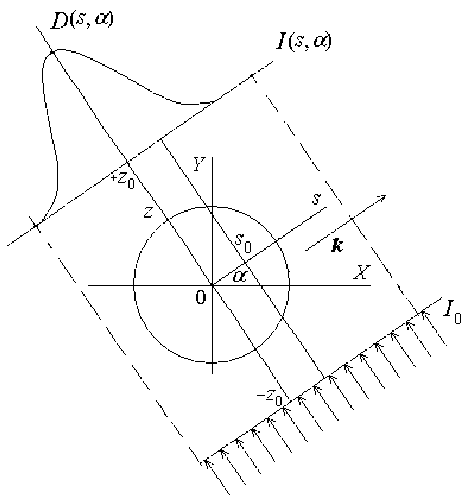
Рис. 4. Схема облучения патологического очага рентгеновским излучением

разование Радона представляет собой проектирование линейного коэффициента поглощения ц ( X , Y ) , как функции двух переменных, на ось s рис. 4.

Рассмотрим важный с практической точки зрения случай зависимости линейного коэффициента поглощения от координат в виде гауссовской кривой:

X ² + Y Y ~ 9

ц ( X , Y ) =        e ^{2 ст} ,                        (21)

GV 2п где ст — постоянная величина с размерностью длины.

Подставим (21) в формулу (20) и перейдем к системе координат s , z по формулам (9) и (10). В результате получим:

D ( s , a ) =

+ z ₀

= J ц ( s cos a- z sin a, s sin a + z cos a ) dz = (22) - z ₀

2  2               22

+ z 0 X + Y                + z 0 s + z

= —¹      e ²^² dz = —1= [ e ²^² dz .

стV2n                    стV2n

• ^{- z} 0                           ^{- z} 0

В (22) учтено X ² + Y ² = s ² + z ² .

Заменяя в (22) пределы интегрирования на бесконечности, т. к. интегрирование идет по все- му патологическому очагу, имеем:

D ( s , a ) =

ст V2n

+да s ² + z ²            s ²

J e ^{2 ст} 2 dz = e ^{2 ст} 2 .

-да

На рис. 4 показан график рентгено-оптической плотности, как проекция линейного коэффициента поглощения на ось s .

Далее поставим задачу восстановления линейного коэффициента поглощения на основе его

проекции.

Найдем Фурье-образ линейного коэффициента поглощения [4]:

ц (к, а) = да                                    да s

= -    D ( s , а ) e - iks ds = - e 22 2 e - iks ds = (24)

2n                      2n

-да                           -да да - s2                            _ k 2g2

= — e 222 cos (ks) ds = 2— e 2 .

2n                        2n

-да

нельзя. Однако, это не является существенным, т. к. общий результат интегрирования мы знаем.

Возможно иное представление формулы (26). Записывая Фурье-образ линейного коэффициента поглощения для определенной линии проектирования с уравнением s - s о = 0, найдем:

да

ц (k, а) = Y j D (s, а)

-да

e

-

iks

ds =

да

= — I* D (s - so, а) e ik(s s0)ds = 2n

-да

да

= — j D (s - so, а) ds.

-да

При нахождении (24) воспользовались четностью функции D ( s , а ) [5].

Полученный Фурье-образ одномерный, т. к. не зависит от угла а. Поэтому используя одномерное обратное преобразование Фурье [6], найдем:

Подставляя (27) в (26), получим:

ц( X, Y ) =

да 2n

= 7“ J f ц (k, а)

2n

e ik ( X cos а+ Y sin а )

+да

D (s) = j eiksdk =

-да

2п да

= 7"f P(k, а)

2n

e^lkskdkd а =

+да

=

72л

-да

_ к V         - s ²

e ² e^iksdk = e ²<

2п да

=D(s- s0, 2n

0 -да

а)h (s) dsd а,

что совпадает с (23).

Для полного восстановления линейного коэффициента поглощения ц ( X , Y ) нужно использовать обратное преобразование Радона (18) и формулу (24):

Ц( X, Y ) =

да 2п

=        (Р ( к , а )

2п

ik ( X cos а+ Y sin а )

e               kdkd ex

да 2п к ²о²

² 3 j j e ~"Г" e^{ik (} X ^{cos а+ Y sin а)} kdkd а =   (26)

( 2п ) 2 0 0

где h ( s ) = 1^0 0* e®^kskdk — т. н. функция фильтра, которая также может быть определена через обобщенные функции.

При осесимметричной функции линейного коэффициента поглощения от координат, восстановление ее по одной проекции, по крайней мере, в принципе, возможно. Эта возможность связана с независимостью рентгено-оптической плотности D ( s , а ) от угла а, (25).

Если же функция ц ( X , Y ) не симметричная, то для восстановления ее необходимо знать и другие проекции. Причем, чем более несимметричная функция, тем больше проекций нужно

22 да k ст -^ j e " ~ ( 2п ) 2 0

< 2п j eik(X cos

V 0

) а+Y sin а) d а

kdk

- X ² + Y ²

___1___ _e    2ст ² 2 Т2Л

К сожалению, найти аналитически интеграл ₁2n ik ( X cos а+ Y sin а )

J o e d а не представляется возможным. Результат интегрирования лежит в области обобщенных функций [7], поэтому последовательно вычислить все интегралы в (26)

знать.

На практике реконструкция функции ц ( X , Y ) осуществляется двумя способами: алгоритмом с использованием преобразований и алгоритмом с использованием разложения в ряд [1].

В первом случае реконструкция изображения осуществляется по принципу графического построения фигур Лиссажу на основе проекций D ( s , а ) [2]. Преобразования удобно осуществлять в полярной системе координат. Громоздкие формулы, пригодные для использования на ЭВМ представлены, например в [1].

Чаще применяют численную реализацию формулы обратного преобразования (28), разлагая подынтегральное выражение в ряд.

Заключение

Рентгеновская компьютерная томография является современным и эффективным методом диагностики заболеваний внутренних органов, в частности, выявления новообразований.

С математической точки зрения метод основан на преобразовании Радона, позволяющем осуществить проектирование двумерной функции линейного коэффициента поглощения на линию, перпендикулярную направлению рентгеновских лучей. Это позволяет найти необходимое число проекций патологического очага в организме, направляя рентгеновские лучи под разными углами в исследуемом сечении. В дальнейшем, используя одну из возможных методик, осуществляется реконструкция патологического очага в исследуемом сечении.