Некоторые особенности взаимодействия радиосигнала с турбулентной атмосферой

Сверхвысокочастотное электромагнитное излучение (СВЧ-излучение) с длиной волны Х = = 1–10 см и ультравысокочастотное электромагнитное излучение (УВЧ-излучение) с длиной волны X = 10 см - 1 м широко используется в телевидении и радиолокации.

Эти виды электромагнитного излучения при отсутствии атмосферы в области гравитационного поля планеты распространяются прямолинейно, что ограничивает радиосвязь на этих волнах расстоянием 40–50 км. Более длинные волны дифрагируют на сферической поверхности Земли, что является одной из причин приема радиосигналов за пределами прямой видимости. Однако наличие атмосферы также ведет к возможности восприятия СВЧ- и УВЧ-излучения за пределами горизонта планеты. Это, в частности, связано с отражением излучения от ионизированного слоя в верхних слоях атмосферы, в тропосфере на высоте 10–12 км в умеренных широтах. Кроме того, эффект восприятия этих излучений за пределами горизонта связан также с турбулентностью атмосферы, в частности стратосферы на высоте 12–50 км с относительной диэлектрической проницаемостью е® 1.

Процесс распространения электромагнитных волн в атмосфере ранее исследовался многими учеными, в частности [1–5].

Взаимодействие электромагнитного излучения и турбулентности атмосферы с физической точки зрения является взаимодействием детерминированного электромагнитного волнового процесса со стохастическим турбулентным волновым процессом.

Целью настоящей статьи является анализ влияния турбулентных пульсаций в атмосфере на электромагнитное излучение.

• 1.    Дифференциальное эффективное сечение рассеяния ультракоротковолнового электромагнитного излучения в турбулентной атмосфере

При анализе распространения ультракоротковолнового электромагнитного излучения в атмосфере в диапазоне X = 10 см - 1 м ее приближенно будем считать неэлектропроводящей средой с диэлектрической проницаемостью е = n ² и магнитной проницаемостью ц = 1, где n - показатель преломления вещества атмосферы.

Система уравнений Максвелла для электромагнитных волн, распространяющихся в атмосфере, имеет вид

1 dH c dt ’

rot E =

„ 1 d D rot H =-- , c d t	(2)
div D = 0 ,	(3)
div H = 0.	(4)

В уравнениях (1)–(4) Е и Н – напряженности электрического и магнитного полей в электромагнитной волне, D – электрическая индукция в ней, t – время, с – скорость света в вакууме, примерно равная скорости света в атмосфере.

Материальное уравнение запишем в виде

D = s E .                                              (5)

Будем считать, что показатель преломления атмосферы незначительно отличается от единицы вследствие флуктуации ее параметров: давления, температуры, влажности и т. д. Поэтому полагаем n = 1 + n / ,                                                  (6)

где n / - случайные пульсации показателя преломления. Величина n / имеет значение порядка 10 - 8 -10 ^{- 6} [6].

Учитывая s = n2, а также n/ « 1, находим s = 1 + 2n/ + n/2 ® 1 + 2n/ = 1+ S.                      (7)

Пульсации диэлектрической проницаемости s / = 2 n / , несмотря на их малую величину, приводят к рассеянию электромагнитных волн в атмосфере.

Учитывая синусоидально-колебательный характер электромагнитных волн, уравнения (1) и (2) можно записать в виде, исключающем временные производные напряженностей полей в волне: rot E = ik H ,                                          (8)

rot H = - ik D .                                        (9)

Плотность потока энергии электромагнитных колебаний – вектор Пойнтинга [7] имеет вид

S = — ( E x H ) .

4пЛ     '

Из уравнения (8) найдем напряженность магнитного поля

H = —- rot E . k

Подставив (11) в (12), найдем зависимость вектора Пойнтинга только от напряженности электрического поля в волне:

S = — (e x H ) = —ci- ( e x rot e ) .

4пЛ     '    4 n k

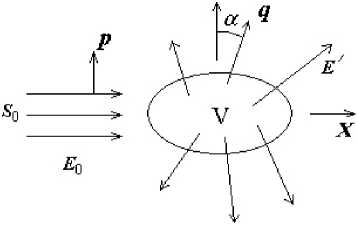
Рис. 1. Рассеяние плоской электромагнитной волны (вектора Пойнтинга) объемом V с турбулентными пульсациями

Fig. 1. Scattering of a plane electromagnetic wave (Poynting vector) by volume V with turbulent pulsations

Пусть на некоторый условно выделенный объем V , рис. 1, в котором имеются турбулентные пульсации атмосферы, падает плоская электромагнитная волна с напряженностью электрического поля в волне:

E o = p A _o ё ^kX ,

где Х – координата распространения падающей волны, p – единичный вектор в плоскости колебаний вектора Eo, перпендикулярный направлению распространения волны, т. е. волновому вектору k, À0 – амплитуда волны, kX – фаза волны. Временную составляющую фазы не учитываем, т. к. используются уравнения Максвелла в виде (8) и (9).

Соответствующая этой волне плотность потока энергии, согласно формуле (12), равна

So (X ) = ci

4 n k

Г

^E o

V

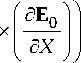
= - ^ ( P A ° e i kX x P A o e i kX * ^k ) = A k e “ • 4 П k                        4 П k

2 где учтено P = 1.

Учитывая, что вектор k направлен вдоль координаты Х , находим среднее по длине волны ( X = = 2 п / k ) значение вектора Пойнтинга:

2 п

2 k

S 0 = A ^k A f ( Re ( e i ² kX ) ) dx = 4 n k 2 n

cA ₀ ² k k

4 n k 2 n

Г ~          )

k j cos ² ( kX ) dx 0

cA ₀ ² k

8 n k

Напряженность электрического поля в объеме V можно представить в виде

E = E 0 + E / , (16) где E / - соответствует рассеянным электромагнитным волнам.

Исключим из системы (8), (9) напряженность магнитного поля, находя ротор уравнения (8): rotrot E = ik rot H = k 2 D .                         (17)

Следовательно, k2 (D0 + D/) = rot rot (E0 + E1), где Do = S0E0 = Eo, т. к. So = 1 - диэлектрическая проницаемость невозмущенной атмосферы, D1 - турбулентные пульсации электрической индукции. Учитывая, согласно (17), k2Do = rotrotEo, находим уравнение для пульсационных электрических характеристик:

k 2 D / = rotrot E / ,                                   (18)

В соответствии с (5) и (7) имеем

D = (1 + 2 n/)E или Do + D/ = (1 + 2n/)(E0 + E/).

Следовательно,

D _o + D / = ( E _o + 2 n ¹ E _o + E¹ + 2 n ¹ E / ).

Учитывая D o = E o и полагая 2 n / E o + E ¹ » 2 n / E ¹, имеем

D / = E / + 2 n ¹ E _o.                                      (19)

Исключая из системы уравнений (18), (19) величину E / , находим k 2 D / = rotrot( D^ - 2 n / E o ). Учитывая формулу векторного анализа rot rot D / = = grad (div D / ) - A D / и формулу (3) в виде div D / = 0, имеем

ikX1 + ik| Х-Х1| = i kX1 + ik(|X|-qXi) _ ik|X| i(k-kq)Xi = e                   = e 1 e , запишем (21) в виде

E1 (X) = д f         i k|x|      /,

A o           p e      f ¹ \ i ( k - k q ) x,

= -°-rot rot^-j—i— n (X,, ) e^      ' ¹ d X, .

2п            X J V 171

Учитываем, что

rot(rot) = V x ( Vx ) = q x ( q x )

а также

rot

f ik X ) pe rot , ,

_k 2 _eik X *

( A + k ² ) D / =- rot rot (2 n / E o ).

Решение волнового уравнения (20) со случайной правой частью с использованием формулы (13)

имеет вид

D ¹ ( X ) =

= —rot 4 n

rot J ² n ( X 1 ) E o ( X 1 )

I V

e k ^{x - x} 1 I X - ^X 1

) d X 1

j

= ^ rot rot p J n ( X 1 )

e i kX 1 + ik |X - X 1|

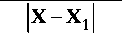
) d X 1

Пусть q = X / X - единичный вектор направления исследования, рис. 1. Полагаем, что вне объема V пульсации отсутствуют, поэтому n ¹ = 0, S = 1 и D = E , а также (5), (6). Величина X ₁ лежит внутри объема V , а Х достаточно далеко от этого объема, поэтому в знаменателе (21) можно величину |х - Х 1| заменить |х - Х 1| * |х| - расстоянием до точки наблюдения. Кроме того, полагая | X - Х 1| = |х - q X 1| = |х| - qX 1 и

d ²

5| X| 2

= ( q ^x( q ^x p ) )

( ( q ^x p )^x q ) .

d ²    e ik ^Xl

d |X| 2    ^X|

В связи с тем что длина электромагнитной вол-

ны мала по сравнению с расстоянием до точки наблюдения |х| » X , при нахождении производной знаменатель считаем приблизительно постоянным, т. е. фактически используем плоскую геометрию. В результате получаем

2 ikX e/ (х )=k4r

G ( ( q ^x p )^x q ) .

где

G = J n / ( X 1 ) e ⁽ k k ^{q ) X 1} d X 1 V

– параметр, характеризующий турбулентные пульсации атмосферы.

Вектор ( q x p ) x q = |sina|, где a - угол между векторами р и q , рис. 1. Вектор ( q x p ) x q перпендикулярен вектору q .

Найдем плотность потока рассеянной электромагнитной энергии по формуле (12):

S / =- _ £ L ( e/ x rot E / ) = 4 n k

• ( ci cl

—г E

4 n k

V.

ci ^f k ⁴ A ²

q ⁰

8 n k    4 n ²

ci d „1 2

--q —i—г E

8 n k V⁴d |X|     J

G ² |sin a| 2

-    2 ik\ Xl )

d e dх1 |x|2 v

^Lq JAL ^{8 n k} V 4 п ² |x| ²

G ²

)

|sin ^a|^{2 2} ike² ik ^Xl

J

c

8 п

42 _q kA ₀

4 п 2 X 2

)

2       2   2 ik X

G sin а 2 e ^{1 1}

ck ⁴ A 0 |^sinа| ² G 2

32 п 3 |x| ^{2      4}

При выводе учтено среднее по длине волны значение Re( e 2 k X ) = 1 / 2.

Дифференциальное эффективное сечение процесса рассеяния электромагнитных волн объемом V равно

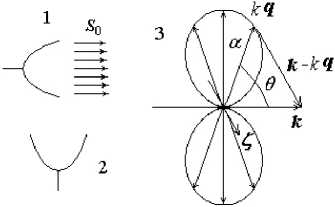
Рис. 2. Схема приема электромагнитных волн, рассеянных на турбулентных пульсациях атмосферы, 1 – излучающая антенна, 2 – приемная антенна, 3 – угловое рассеяние волн

Fig. 2. Scheme for receiving electromagnetic waves scattered by turbulent pulsations of the atmosphere, 1 – emitting antenna, 2 – receiving antenna, 3 – angular wave scattering

dP d g = i—,.

S 0

Поток энергии (мощность) dP электромагнит-

ных волн, рассеянных в телесный угол dQ в направлении q, учитывая (24), равен ck4A2 |sin а|2 о dP = |S/ X| dQ =----—Lg2dq.           (26)

Подставляя в (26) формулу (15), находим

k4 Isinа|2             4    2 о dg = -J----Lg2dq = k sin а g2dq.

4 п ²               4 n ²

Двухточечную корреляционную функцию

B nn ( ^X 1 - ^X 2 )= ( n¹ ( ^X 1 ) n¹ ( ^X 2 ))

(угловые скобки, как обычно, означают пространственное осреднение) с помощью Фурье-преобразования запишем через Фурье-спектр турбулент ^ности F nn ^{( Z ):}

B nn ( ^X 1 - ^X 2 ) =                                   (29)

= J exp ( - i Z ( X i - X 2 ) ) ^F nn ( Z ) d Z .

Таким образом, дифференциальное эффективное сечение процесса рассеяния электромагнитных волн турбулентными пульсациями атмосферы подчиняется закону четвертой степени Рэлея:

d g ~ k ⁴

16 n ⁴

X ⁴ ’

На рис. 2 показано распределение дифференциального эффективного сечения в зависимости от угла а .

2. Влияние турбулентных характеристик атмосферы на рассеяние электромагнитного излучения

Исследуем более подробно параметр

G = J n / ( X 1 ) e ^{( k} - ^k q ^{) X 1} d X 1 ,

V характеризующий турбулизацию атмосферы. Волновой вектор k - kq представляет собой разность между волновыми векторами падающей и рассеянной волн, рис. 2.

Для упрощения анализа турбулентность будем считать однородной и изотропной, т. е. она имеет количественно везде одну и ту же структуру и ее статистические характеристики не зависят от направления.

В данном случае Z является волновым вектором турбулентного спектра. При взаимодействии электромагнитной волны и турбулентности происходит взаимодействие двух волновых процессов: детерминированного электромагнитного волнового процесса и стохастического турбулентного волнового процесса. Волновой вектор, представляющий разность между волновыми векторами падающей и рассеянной электромагнитных волн k - k q , полагаем пропорциональным волновому вектору турбулентного спектра Z , рис. 2. Это будет обосновано далее.

Таким образом, средний квадрат параметра турбулентности G равен

G^G 2) = JJ B nn ( ^X 1 - ^X 2 )^{X                         (30)}

VV x exp (-iZ(X1 - X2)) dX1 dX2.

Постоянный коэффициент пропорциональности между волновыми векторами k - k q и Z для дальнейших преобразований несущественен, и его полагаем равным единице. В дальнейшем его численное значение уточним.

С другой стороны, используя Фурье-спектр, имеем

= 8 л ³ V

Z/

J ~J exP(iZr)dr Fnn (Z) dZ 8n3^

® 8 п ³

V

где r = Xi - X2. Весовая функция f (Z) = ^3 J exp (izr) dr, интеграл от которой по всему волновому пространству равен единице [6]. Поэтому функция f (Z) изменяется незначительно и ее можно вынести за знак интеграла. Величина

Z             5

J F nn ( Z ) d z ~ Z²

в достаточно большом диапазоне модулей волновых векторов [8]. Этому же закону подчиняется средний квадрат параметра турбулентности GG2(Z)^. Сам параметр турбулентности подчиняется закону, близкому к линейному G (z) ~ Z54, а спектральная функция турбулентности приблизительно подчиняется закону d53

F nn ^(z) ~ d k^Z 2 ~ ^Z 2 .

Пусть 9 - угол рассеяния между волновым вектором k падающей электромагнитной волны и направлением q рассеянной волны, рис. 2. Тогда из равнобедренного треугольника

| k - k q| = 2 к

9 sin —

Учитывая к = 2 п / X , находим величину

d =

X		= 2 п = 2 п
2	9	| k - к q| 5Z ’
	sin — 2

где 5= k - к q / Z - параметр, показывающий во сколько раз электромагнитный волновой вектор k - к q больше турбулентного волнового вектора Z .

Формула (32) называется уравнением Вульфа – Брэгга для пространственной дифракционной решетки. Величина d – аналог периода решетки, т. е. расстояние между структурами, рассеивающими электромагнитные волны. Следовательно, турбу-

лентность атмосферы можно с некоторым приближением представить в виде пространственной дифракционной решетки.

Можно уподобить величину d масштабу турбулентности. В изотропной турбулентности d « 0,75 / Z [8]. Сравнение (32) с этой формулой подтверждает пропорциональность волнового вектора k - к q , т. е. разности падающего и рассеянного турбулентностью электромагнитного излучения и волнового вектора турбулентного спектра Z . Кроме того, можно оценить коэффициент пропорциональности 5 между этими векторами 2 п / 5 = 0,75 и 5® 8,37, так, что k - к q ® 8,37 Z .

Заключение

Рассеяние ультракоротковолнового электромагнитного излучения на турбулентности атмосферы приводит к различным эффектам, в том числе влияет на дальнюю радиосвязь на ультракоротких волнах. Дифференциальное эффективное сечение рассеяния радиоизлучения на турбулентных флуктуациях показателя преломления относительно длины волны подчиняется закону Рэлея, а геометрически – квадратичному синусоидальному закону с максимумом, перпендикулярным первоначальному направлению излучения.

Показано, что турбулентность атмосферы при взаимодействии с радиоволной можно представить в виде пространственной дифракционной решетки. Найдена зависимость эффективного периода этой решетки от параметров электромагнитной волны и турбулентности.

С физической точки зрения взаимодействие электромагнитного излучения и турбулентности атмосферы является взаимодействием детерминированного электромагнитного волнового процесса со стохастическим турбулентным волновым процессом. При этом волновой вектор, характеризующий разность падающего и рассеянного турбулентностью электромагнитного излучения, пропорционален волновому вектору турбулентного спектра. Длина волны рассеянного электромагнитного излучения примерно на порядок меньше масштаба турбулентности.