Некоторые применения теории рядов при решении экономических задач

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 519.23                                        

В настоящее время умение применять теоретические знания при решении практических задач становится решающим фактором для изучения любой дисциплины. В частности, исходя из многолетнего опыта преподавания бизнес математики в экономическом вузе, авторам представляется необходимым продемонстрировать решение некоторых экономических задач при помощи математического аппарата [1, 2].

Если мы не сможем улучшить математическое образование, учитывая потребности современного мира и студентов, мы находимся в опасности превращения математики во все более «мертвый язык» и отчуждения групп студентов, математический потенциал которых останется неразвитым [3, 4].

Во многих случаях инвестиционных проектов производства вклады возвращаются одинаковым потоком платежей или другим видом выплат. Его называют «аннуитетом». [5].

(ос) CD

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №3. 2024

Например, можно платить фиксированную сумму для гарантированных пенсионных выплат £14,000 в течение 5 лет. Если одинаковый поток платежей возвращается в течение n лет по процентной ставке i %, его сегодняшняя стоимость:

PV = a (1 + i)  + a (1 + i)  +... + a (1 + i)

.

Известно, что эта последовательность состоит из геометрической прогрессии. Для ее вычисления необязательно вычислять отдельно каждое слагаемое и затем складывать. Можно воспользоваться компьютером или формулами. Существуют и бессрочные аннуитеты [6, 7]. Например, если по номиналу £100 выплачиваются фиксированные 6%, то денежная сумма £6 называется «вечной» рентой. NPV такого аннуитета по процентной ставке i :

66   6

1+++

1 + i ( 1 + i ) 2          ( 1 + i ) "

, здесь n длится бесконечно. Каждый следующий член уменьшается, но сумма этой последовательности продолжает расти. Сумму этой бесконечной последовательности чисел нельзя вообразить без формулы бесконечно убывающей геометрической прогрессии.

Сумму геометрической прогрессии можно вычислять при помощи калькулятора. Для более сложных случаев приходится вывести формулу.

Сумма первых n членов геометрической прогрессии:

GPn = a + ak + ak2 +... + akn-1                                       (1)

Умножив каждое слагаемое на k, kGPn = ak + ak2 +... + akn-1 + akn , вычтем (1)

GP = a + ak + ak2 +... + akn-1 .

Получим

( k - 1 ) GP =- a + ak ⁿ .

Отсюда

Gp = - a + ak" = - a (1 - k") = (-1) a (1 -k) = a (1 - kn) n k -1        k -1       (-1)(1 -k)      1 - k

Таким образом, формула суммы геометрической прогрессии:

GP n

a (1 - k")

1 - k

В следующих примерах увидим применения формулы к простым последовательностям.

Пример. Найдите сумму геометрической прогрессии, пользуясь формулой.

15      45    135   405   1,215        3,645

Решение. Это прогрессия из 6 членов, каждый следующий получен из предыдущего умножением на 3, т. е. a 15

k = 3

n = 6

Из формулы суммы геометрической прогрессии получаем:

a ( 1 - k " )    15 ( 1 - 3⁶ ) 15(1 - 729)   15( - 728

GP = -^----L = —^----Z=—(-----) = —(----) = 15 x 364 = 5,460

"    1 - k       - 2         - 2          - 2

Обозначим через R годовые выплаты на срок n лет с процентной ставкой i , тогда

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №3. 2024

PV = — +

1 + i

RR ^2+---+7,—

n

.

Первый член этой прогрессии

R

a =---

1 + i

, знаменатель

k = ~

1 + i

.

Отсюда

R

a ( 1 — k n )    1 + i

PV =  ----’- =---

1—

n

R

—

n

R

1 — k

1--1

1 + i — 1

i

1 + i

Таким образом, для аннуитета:

n

PV =

i .

Из школьной программы известна задача следующего типа. Лягушка сидит на дощечке в центре бассейна. Радиус бассейна 10 м. За сколько прыжков лягушка достигнет края бассейна?

Предполагается, что при каждом прыжке лягушка попадает на дощечку. Пройденный лягушкой путь за n прыжков состоит из геометрической прогрессии:

5 + ( 0,5 ) 5 + ( 0,5 ) 2 5 +... + ( 0,5 ) n ^{— 1}5 .

При достаточно больших n эта сумма растет, но никогда не достигает 10 метров. При бесконечно большом числе прыжков общее расстояние достигает 10 метров. Таким образом, имеем геометрический ряд. Этот ряд сходится к 10.

Геометрическая прогрессия может расходиться. Например, последовательность

60     90     135...

можно записать в виде геометрической прогрессии

40      40 ( 1.5 )      40 ( 1.5 ) 2         40 ( 1,5 ) n

.

Видно, что каждый следующий член больше предыдущего. Таким образом, при увеличении числа слагаемых сумма бесконечно увеличивается. Сам последний член 40(1,5)ⁿ бесконечно велик. Сходимость или расходимость ряда с геометрической прогрессией зависит от ее знаменателя k .

Если | k |>1, то ряд расходится.

Если | k |<1, то ряд сходится.

Причина использования абсолютного значения в том, что знаменатель прогрессии может быть и отрицательным.

Рассмотрим формулу вычисления суммы сходящейся геометрической прогрессии (например, как вечная рента):

a (1 — kn)

GP =—---- n     1 — k

Это можно записать:

GP n

a

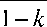
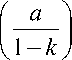
kn

Если ¹ <  k < ¹, то ^к ^ 0 при n^^ , поэтому пропадает второй член и сумма равна

GP n

a

1 — к

Теперь применим формулу (2) к задаче о лягушке. Общее расстояние прыжков

Z 5 ( 0,5 ) " = 0

В этой геометрической прогрессии k= 0,5 и a= 5. Сумма бесконечных слагаемых

a

1 — к 1 — 0,5

— = 10

0,5

Пользуясь этой формулой, можно найти следующий пример.

Пример. Вклад на неограниченный срок платеж произведется через 12 месяцев,

PV для

метров.

вечного аннуитета. Это объяснит

составил найдите

£6 в год. Если при этом первый PV этого аннуитета. Примем

инвестиционную процентную ставку вклада за 15%.

Решение.

PV = -6- + A + ...+ -A_

1,15   1,15²        1,15 ⁿ

,

a = —

В этой геометрической прогрессии    1.5

здесь n →∞.

к = —

и

1,5 т

,   . Так

как

I к <  1

, прогрессия

сходится. Отсюда, можно записать упрощенную формулу для PV: 6

NPV = — = -1 — к J

1,15

—

1,15

Л

1,15 1

—

-J-1

1,15 J

1,15 — 1

-6- = £40 0,15

Предположим, аннуитет выплачивает капитала R . Для этого аннуитета:

i % годовых, начиная с

12 месяцев, стоимость

PV = R (1 + i)-1 + R (1 + i)-2 +... + R (1 + i)-n

, здесь n →∞.

a = R (1 + i) ‘                  к = (1 + i

Первый член этой геометрической прогрессии            и знаменатель

Поэтому, из формулы бесконечно убывающей геометрической прогрессии:

_PV = a = ^R ( 1 + i ) — ¹ 1 — к 1 — ( 1 + i ) ^{— 1}

R

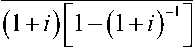
RR

1 + i — 1 i

Таким образом, формула для вычисления PV для вечной ренты:

PV = R

i

Применив эту формулу в примере, найдем:

PV = — = £40 0,15

Эта формула облегчает вычисления.

Определение. Выражение

^a 1 , a 2 , a з ,. .., a n ,.

да

E a = a + a + ... + a ,...

n12     n, n=1

составленное из членов числовой последовательности называется числовым рядом.

Здесь a ¹, a 2 ,a 3 , . ,a n ^,. называются членами ряда, а a n общим членом ряда. Из определения видно, что ряд определяется суммой счетного числа слагаемых, составленных по определенному правилу.

„        S. = a.,  S₇ = a. + a..,...S„ = a. + a.. + ... + a„

Суммы 1    1     2    1    2    n    1    2         n , составленные из конечного числа первых членов суммами этого ряда.

Учитывая счетность членов ряда, можно видеть,

S, , S,S

^{1 , 2 ,  , n ,} составляют числовую последовательность.

ряда,

что

называются частичными сами частичные суммы

Определение. Если последовательность частичных сумм {Sn} имеет конечный предел да

£ imSn = S         E an n^да      , то ряд n=1   сходится, а предел S называется суммой ряда и записывается в да

. E a- = S виде -=1          .

{ S }       .   .                           A        Z А

Определение. Если последовательность n не обладает конечным пределом (предел бесконечен или не существует), то ряд (3) называется расходящимся.

Например. Исследуйте ряд:

b + bq + bq ² + ... + bq^{n - 1} + ... = E bq" - 1 ,(b ^ 0)

n = 1

Сумма первых ⁿ его членов определяется формулой:

_ b + bq n i - q

b

^{1 -} q

+

b

1 - q

q

n

Для суммы этого ряда предыдущие утверждения зависят непосредственно от q .

1) Если

I q <  1       lim q n =⁰                   ~

, т. к. ⁿ ^^да        , имеем конечный предел

S = £ im Sn n ^да

b

^{1 q} . Т. е. при

b

I q | <¹

ряд сходится, а его сумма вычисляется по формуле       q q > 1            £imqn = да

£ im Sn n ^да не существует, при

• 2)    Если      , очевидно, n ”         . Поэтому при ^q

£ imSn =да n >z        , и ряд расходится.

• 3)    Если q ¹, имеет S n вид ряд расходится.

• 4)    Если q = ^{— 1} ряд имеет вид:

S = S.

Для такого ряда ^{n 2 m}

S = b + b +... + b = b • n                       £im Sn =да n                        . В этом случае, т. к. n >да        ,

b - b + b - b + ... + ( - 1) n ^{- 1} b + ...

= 0, S n = S 2 m + 1 = b, ( m = 1,2,3...)

.

А это означает не

„                         £ im Sn существование предела n >да . Поэтому и при q     ряд расходится.

Теорема. Если ряд (3) сходится, любой его остаток сходится и наоборот, если сходится остаток ряда, он сам тоже сходится.

Если равна k’S

да a n ряд n=1    сходится,

.

Если

равенство

ряды да

Z (an n =1

да

Z an n=1

и

да

да

Z b .

n = 1

да

Z ь .

его сумма S, то и ряд ⁿ = 1

± ^b n ) = Z a n ± Z ^b n

да

Z ( a n сходятся, то и ряды ⁿ = 1

да

n = 1

n = 1

.

да

= Z kan n=1    сходится и его сумма

± ^b n )

сходятся и имеет место

Необходимое условие сходимости рядов да

Z a n

Теорема. (Необходимое условие сходимости рядов). Если ряд n=1    сходится, при стремлении порядкового номера к бесконечности общий член an стремится к нулю, т. е. £ iman = 0 n >да

.

I im an

Следствие. Если для ряда не выполняется условие ⁿ >^да

Например. Ряд

да      1                                   С

Z (1 + — )                £ima_n = £im 1 1

^^       2                         n >x       n>да I n=1     n расходится, т.к.              v

= ⁰      л Д

, то ряд расходится.

+ X | = 1 ^ 0

n J

.

Условие

£ im an n >да

= 0

да

Z an ряд n=1 сходится, то

Например, хотя

является лишь необходимым условием сходимости ряда. Т.е. если n

£ im an = 0         £ im an = 0      Z an n>да       . Но при n>да       , ряд n=да   не всегда сходится.

1     !     1     1             1

> - = 1 +  +- + — + - + •••

^ И           4

для гармонического ряда ^{n = 1 n}                т     выполняется

£ im a_n условие ⁿ >^да

n

= 0

, он расходится.

Признак сравнения

Определение. Если для всех n  1,2,3,• • an > 0, то ряд да a} + a2 + a2 +-----+ an +— = Z a> n-1

называется рядом с положительными членами .

да да

Z b n n = 1

.

Z a n ,

Пусть даны ряды с положительными членами ⁿ = 1

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №3. 2024

W от

I bn n=1

Теорема. Если для всех n = ^1,2,3,"'

,

I a _n сходится, ряд ⁿ = 1 сходится.

Теорема. Если для всех ^{n 1,2,}3’--- an <  bn расходится .

от

I an n=1

,

от

I b .

расходится,  ⁿ = 1     тоже

Пример. Исследовать ряд

111  1

1 + ^ + -f + ^ + ••• + ^ + ■■■

n

.

" ⁺ П ⁺ ■ , при n = ¹ , ^2,3 , -

1 ++   + •

Решение . Возьмем гармонический ряд    2  3  4

1 < х видно, что n n , и гармонический ряд расходится. Поэтому по теореме, данный ряд расходится.