Некоторые проблемы обеспечения качества преподавания математических дисциплин в современных условиях

Изучению математических дисциплин в образовании инженера принадлежит особая роль. По словам Иммануила Канта: «В каждой естественной науке заключено столько истины, сколько в ней есть математики» [1]. Отечественные традиции преподавания точных наук, в частности математических, в технических вузах всегда сочетали глубокое изучение теории и практики, закладывая тем самым фундамент для освоения прикладных наук и специальных курсов. По многочисленным свидетельствам, качество преподавания математических дисциплин не только не уступало, но в чем-то превосходило как европейские, так и мировые стандарты.

К сожалению, в последние годы ситуация меняется не в лучшую сторону. Предполагалось, что единое образовательное пространство в рамках Болонского процесса позволит национальным системам образования взять все лучшее, что есть у партнеров, и вывести их на новый уровень. Однако этого не случилось по ряду причин. В частности, не были приняты во внимание существенные различия в системе обучении украинских и европейских школьников. Многочисленные нововведения в нашей средней школе не смогли усилить те качества выпускника, которыми могло бы гордиться национальное школьное образование. В результате выпускники школ не всегда имеют подготовку, на основе которой можно эффективно изучать математические дисциплины в вузе. Внешнее независимое тестирование по математике на сегодняшний день почти не содержит открытых задач, то есть заданий, требующих соответствующих доказательств или применения оригинальных методов решения. Приходится констатировать, что упор на тестовую систему преподавания не способствует развитию логического мышления и умению принимать решения. Школьные программы раздуты за счет включения в них фрагментов из высшей математики, которые к тому же изучаются весьма поверхностно! В то же время у школьников имеются заметные пробелы по элементарной математике (в частности, алгебре и тригонометрии). Конечно, встречаются исключения в виде хорошо подготовленных абитуриентов, но таких исключений становится все меньше с каждым новым набором. Более того, по их собственному признанию, своими успехами они обязаны скорее индивидуальной подготовке, чем школьной. Заметим, что с подобными проблемами сталкиваются и наши коллеги в России. Так, профессор факультета вычислительной математики и кибернетики (ВМК) МГУ В.А. Сухомлин отмечает: «В секторе математического образования ситуация оказалась катастрофической. По существу отовсюду слышится, что средняя школа просела за последние годы настолько, что ниже некуда.

Например, на совете факультета ВМК МГУ по итогам первого семестра 20122013 учебного года руководством факультета дается рекомендация преподавателям, ведущим занятия по базовым математическим предметам на первом курсе, впредь посвящать первые лекции и семинары повторению основных разделов элементарной математики. Также рекомендуется перестроить занятия так, чтобы помочь учащимся преодолеть трудности, связанные с недостаточно развитым у них аналитическим мышлением и логикой рассуждения, с восприятием доказательного подхода.

Есть еще одна беда, которая напрямую связана с ЕГЭ (аналогом нашего внешнего тестирования (авт.)): многие выпускники школ «немые» - не умеют вслух связно излагать свои мысли, свои знания, у них отсутствуют навыки по запоминанию, логическому мышлению, связной речи; они просто не могут запомнить формулировки определений, доказательства теорем. И это, в общем-то, у лучших школьников, студентов сильных университетов. Такого падения общего образования никогда еще не было.

В целом, абсолютное большинство вузовского сообщества оценивает состояние общей школы, в котором она оказалась в результате проводимых МОН реформ, как национальную катастрофу» [2].

Указанная профессором Сухомлиным ситуация чрезвычайно контрастирует с подготовкой школьников в странах западной Европы. В качестве примера рассмотрим Великобританию [3]. С 14 – 16 лет английские школьники целенаправленно готовятся к экзаменам (обычно по 7 – 9 предметам!) на сертификат о среднем образовании GCSE (General Certificate of Secondary Education). Желающим поступить в университеты предлагается двухгодичный (!) курс А-levels. После первого курса обучения сдаются экзамены AS, а после второго – A2-levels. После прохождения 2-годичного курса А-levels они могут поступить в университет. Безусловно, что при таком подходе в университеты поступают не все выпускники школ. А те, кто поступает, проходят основательную предварительную подготовку!

Высшее образование в Великобритании (Higher Education) включает программы по получению степени бакалавра, последипломные программы (магистратура, докторская степень) и МВА (Master of Business Administration). Квалификация МВА подразумевает способность выполнять работу руководителя среднего и высшего звена.

Плюсы и минусы Болонских соглашений

Обратимся к Болонским соглашениям. Большие надежды, связанные с ними, к сожалению, не оправдались. Действительно, некоторые их положения подчас носят чисто декларативный характер и справедливо критикуются в той же Европе. А такие европейские элитарные вузы, как Кембридж, Парижский институт политических наук и т.д. вообще отказались от участия в этом процессе. Бытует мнение, что Болонские соглашения – для тех, кто готов ограничиться формальным узкоспециальным образованием, а для получения фундаментального образования следует выбирать Кембридж, Итон, Сорбонну и т.д. Действительно, как заманчиво не выглядят положения о мобильности студентов и преподавателей, о взаимном признании дипломов и проч., на практике все выглядит не так, как задумывалось. Последнее замечено и в западной Европе, и в странах СНГ. В первую очередь, пострадало качество образования. Так, в последнее время можно наблюдать тенденцию к сокращению количества аудиторных занятий на фоне возрастания времени, предназначенного для самостоятельной работы студентов. Если подобные нормы уместны на старших курсах, где студенты работают над курсовыми и дипломными работами, то на первых курсах, когда вчерашние школьники изучают курс высшей математики, другие фундаментальные дисциплины и при этом должны избавляться от пробелов в школьном образовании, внедрение таких норм контрпродуктивно. Сами студенты признаются, что максимум полезной информации по предмету они получают на лекциях и в лабораториях!

К сожалению, реформирование национальной высшей школы произошло без оглядки на имеющиеся традиции, без тщательного предварительного изучения плюсов и минусов Болонских соглашений. Вместе с тем, система образования, как таковая, имеет определенные особенности, о которых хорошо сказал профессор МГУ В. А. Сухомлин: «Какими особенностями обладает система образования? Что с ней можно делать, а чего нельзя? Одним из характерных ее свойств, которое не учитывается реформаторами, является так называемая унаследованность (legacy). Унаследованные системы за долгое время использования становятся неотъемлемой частью жизни и деятельности многих людей. Когда такие системы начинают заметно отставать от требований современных или грядущих технологий, то встает естественный вопрос об их обновлении. Учитывая наработанную за годы практическую ценность унаследованных систем, их чрезвычайную сложность, а также высокую стоимость их полной реконструкции, для обновления унаследованных систем применяют специальные технологии. Такие технологии позволяют сохранить все полезные функции унаследованной системы, перевести ее на рельсы современных решений, обеспечить гибкую интеграцию со всем информационным миром» [4]. Здесь напрашивается аналогия с «Законом отрицания отрицания» в философии. Добавим, что не будет пользы от внедрения чужеродной системы, которая оправдывает себя только там, где она традиционна. В то же время словосочетания «кредитно-модульная система», «компетентностный подход» звучат красиво, но их внедрение изменений в лучшую сторону содержанию обучения не придает.

Отметим, что традиционные методики преподавания, жесткий контроль качества знаний – все то, что всегда отличало национальное образование, Болонской конвенции не противоречат! Вместе с тем отказ от них и внедрение новых стандартов оценивания знаний способствуют получению лишь фрагментарного образования. Написал студент модуль по узкой теме – переключается на другую. Нет целостной картины той или иной дисциплины. И вообще такой студент не способен видеть целое, поскольку этому его не учат. Ведь все должно быть уложено в «прокрустово ложе» немногих часов, отпущенных на аудиторные занятия. С другой стороны, математика – предмет, для изучения которого необходимо не только его осмысление, но и основательное количество решаемых задач, и знакомство с множеством методик и приемов. Так что уменьшение количества аудиторных занятий (лекций, практических занятий, семинаров, лабораторных работ) отрицательно повлияло на качество подготовки студентов.

В Болонской структуре квалификаций важное место отводится так называемым «Дублинским дескрипторам» [5]. Приведем некоторые детали этого документа, которые основаны на пяти главных результатах обучения, а затем прокомментируем их, учитывая наши реалии (при этом ограничимся только двумя циклами (уровнями) высшего образования).

Итак, что должен знать, понимать и/или уметь студент.

Знания и понимание :

Цикл 1 (бакалавр) – поддерживается продвинутыми учебниками и включает в себя определенные аспекты, связанные с наиболее передовыми знаниями в области изучения.

Цикл 2 (магистр) – составляют основу или возможность для проявления оригинальности при разработке и (или) применении идей, часто в рамках исследовательского контекста.

Применение знаний и понимания:

Цикл 1 (бакалавр) – путем формирования и обоснования доводов.

Цикл 2 (магистр) – понимание и способность решать проблемы в новых и незнакомых контекстах в рамках более широких (междисциплинарных) контекстов.

Вынесение суждений:

Цикл 1 (бакалавр) – сбор и интерпретация значимых данных.

Цикл 2 (магистр) – способность интегрировать знания и справляться со сложными вопросами, формулировать суждения на основе неполной или ограниченной информации.

Коммуникативные умения:

Цикл 1 (бакалавр) – сообщать информацию, идеи, проблемы и решения.

Цикл 2 (магистр) – сообщать свои выводы и использованные для их формулировки знания и обоснование (ограниченный объем) специалистам и неспециалистам (монолог).

Умения в области обучения:

Цикл 1 (бакалавр) - умения в области обучения, которые необходимы для продолжения обучения с высокой степенью автономности.

Цикл 2 (магистр) - умения в области обучения, позволяющие им продолжать обучение в значительной мере самостоятельно и автономно.

Обладают ли наши студенты вышеперечисленными умениями? К сожалению, лишь немногие из них. Скорее, большинство просто не в состоянии четко и внятно выражать свои мысли. Бывают парадоксальные ситуации, когда студент понимает, как следует решать задачу, но не может толком объяснить свои идеи! Все это -результат отказа от традиционных экзаменов, как в школе, так и в вузе!

Отметим и следующий весьма существенный момент. Под надуманными предлогами отменены вступительные экзамены в вузы (и даже собеседование!). Улучшить качество набора можно даже при нынешних условиях, временно увеличив количество принятых на первый курс студентов за счет «соискателей» из числа тех, кто не набрал необходимое для поступления количество баллов. Возникла бы здоровая конкуренция между ними и другими первокурсниками. Зато после первой же сессии можно будет исключать всех неуспевающих, улучшив качественный состав нового набора. Кстати, во Франции прием в вузы происходит без вступительных экзаменов. Необходим лишь документ о наличии среднего образования. Однако там студентов, проваливших экзамены на первой сессии, немедленно исключают! После следующей сессии отсев продолжается. Так идет «естественный отбор» тех, кто серьезно настроен на учебу! Отмена экзаменов в наших вузах негативно сказывается на качестве подготовки студентов. Ведь экзамены дисциплинируют, позволяют студентам составить цельное представление о предмете. Замена экзаменов модульными контрольными работами не является адекватной. Не будет способствовать повышению качества обучения введение новых норм по соотношению количества студентов на одного преподавателя. Вырастет учебная нагрузка, неизбежно произойдет сокращение штатов. О какой научной и методической работе в вузе тогда можно говорить?

Словом, проблем немало. Мы остановились только на самых болезненных из них, а именно:

• -    необходимость улучшения школьного образования;

• -    необходимость совершенствования вступительных кампаний в вузах (с акцентом на качественный отбор);

• -    отрицательные последствия сокращения аудиторных занятий на младших курсах;

• -    необходимость совершенствования системы оценивания знаний. Например, введение, по крайней мере, итоговых экзаменов при завершении изучения того или иного предмета.

Отметим еще одно обстоятельство, которое негативно влияет на качество нашего образования. В Украине действует огромное количество вузов, многие из которых не обеспечены как высококвалифицированными кадрами, так и соответствующим оборудованием, материалами, лабораториями, что приводит к появлению массы людей с дипломами, но без знаний по специальности. Это как раз тот случай, когда количество не переходит в качество.

Ясно, что нужны решительные действия, направленные на исправление допущенных просчетов, о которых сказал в мае этого года на форуме в Харькове «Постсоветский мир 2020: риски, вызовы, сценарии» министр образования и науки Украины Д.Табачник: «Нами неудачно на начальном этапе была скопирована Болонская система, когда мы попытались выставить все ориентиры не только на минимально необходимую планку, но и на наивысшую». [6]. По мнению министра, из-за этого научная среда могла утратить специалистов, в частности, в математике и астрофизике. «Уже через несколько лет имплементации болонского опыта стало понятно, что не надо всех причесывать под одну гребенку. Стоит выставить только самую низкую планку», - добавил он.

Спустя годы, прошедшие с момента подписания Болонских соглашений, специалисты отмечают, что они не только не решили проблем отечественного образования, а, скорее всего, высветили его недостатки. Так, директор Центра тестовых технологий и мониторинга качества образования Игорь Ликарчук, комментируя итоги 2012 года в образовании, заявил, что система высшего образования Украины потерпела «Болонское поражение». «Участие нашего государства в Болонском процессе, о котором так много говорили, оценено «двойкой» по пятибалльной шкале», подчеркнул он.

Итак, проблемы лежат на поверхности, а наличие столь откровенных и даже жестких оценок лишь подтверждают это. Так что предстоит большая и непростая работа по их разрешению.

Использование современных информационных технологий как один из способов повышения качества преподавания

Вновь вернемся к нашим реалиям и остановимся на том, как можно и в нынешних непростых условиях поддерживать наукоемкие преподавательские технологии.

Известно, что еще в далеком 1970 году появилась специальность "Прикладная математика и информатика», созданная выдающимся ученым академиком А.Н.Тихоновым и его научной школой. Ее характеризует сочетание фундаментального математического образования и профессиональной подготовки по использованию современных информационных технологий для решения прикладных задач. С тех пор прошли десятилетия, но потребность в специалистах по прикладной математике и информатике постоянно растет. Более того, в современных условиях такой подход приобретает особую актуальность [7 – 9].

Для внедрения подобного подхода к учебному процессу группой преподавателей кафедры прикладной математики и вычислительной техники НМетАУ был подготовлен и издан учебник, в котором при изучении классического курса высшей математики также предлагается использовать современные информационные технологии, в частности, универсальную математическую среду Mathcad [10]. Это достигается за счет того, что в нем, наряду с изложением материала общего курса высшей математики и большим количеством примеров, иллюстрирующих теоретические положения, почти все «классические» решения дублируются соответствующими решениями, полученными при помощи среды Мathcad.

Такой подход к изучению общего курса высшей математики стимулирует студента к освоению как общих положений курса (без этого невозможно применение вычислительной среды), так и основ Мathcad. И если формальное внедрение новых стандартов процесса образования и оценивания знаний не всегда способствуют получению системных и глубоких знаний, то возможность проверить при помощи Mathcad правильность полученного самостоятельно «классического» решения той или иной задачи делает процесс освоения материала интересным, мотивированным, активным. Возрастает «самостоятельная составляющая» в процессе обучения, что в принципе является хорошим показателем вне зависимости от модели обучения.

Поясним, почему выбор был остановлен на Mathcad. Простота интерфейса среды Mathcad и широкий набор графических, аналитических и численных методов решения математических задач позволяют использовать универсальную программную среду в учебном процессе.

Среда позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет удобный математико-ориентированный интерфейс (совокупность средств, которые обеспечивают управление системой с помощью клавиатуры и мыши). Необходимо отметить, что используемый в среде Mathcad интерфейс достаточно прост и пользователь, который имеет элементарные навыки работы с Word и Excel, может сразу же работать и в Mathcad.

Отметим, в том числе, что среда Mathcad успешно используется для решения задач линейной и векторной алгебры, для отыскания пределов функций, а также производных и интегралов, при суммировании рядов, исследовании их сходимости и разложении функций в ряды Тейлора и Маклорена. Приведем простой пример. Покажем, каким образом решается система линейных алгебраических уравнений методом Гаусса в среде Mathcad. Выбор в качестве иллюстрации такого примера не случаен: математическая модель множества задач из самых разных областей механики, экономики, статистики и т. д. представляет собой именно линейную систему алгебраических уравнений. Таким образом, с подобной задачей приходится иметь дело весьма часто.

Итак, рассмотрим систему линейных алгебраических уравнений вида:

2xj - 3x2 + 4x3 = -6, ■  x 1 + 4 x2 - x 3 =3,

5Xj - 6x2 + 3x2 = -1.

Решение ее традиционным способом опустим, ограничившись лишь решением в среде Mathcad.

В среде Mathcad вводим матрицу коэффициентов системы А и матрицу-столбец свободных членов B .

Продемонстрируем этапы введения, например, матрицы A :

• а)    вводят переменную А :

При этом на экране отображается A :=    ;

• б)    открывают панель операций с матрицами и определителями, подведя курсор к соответствующей кнопке на панели математических инструментов и щелкнув левой клавишей мыши;

• в)    на панели операций с матрицами и определителями нажимают на кнопку формирования матрицы и указывают порядок вводимой матрицы (3х3);

• г)    вводят элементы матрицы.

При этом на мониторе компьютера информация будет отображаться таким образом:

- 3  4

- 6

A : =

• 1   4   - 1; B :=  3

• 3.    Для вывода расширенной матрицы на экран компьютера в среде Mathcad вводят ROZSHM =

5   - 6  3           - 1

После введения матриц А и В необходимо присвоить переменной ORIGIN значение, равное единице. Это выполняется для того, чтобы среда нумеровала строки и столбцы матриц, начиная с единицы.

Итак, вводим

ORIGIN: = 1.

Для того чтобы сформировать расширенную матрицу системы, используется функция augment (A, B). Данная функция добавляет к столбцам матрицы коэффициентов системы A справа столбец свободных членов B. Таким образом, вводится выражение:

ROZSHM := augment ( A , B )

При этом на экране отображается такая информация:

	"2	— 3	4	— 6
ROZSHM: =	1	4	— 1	2
	. 5	— 6	3	— 1

• 4.    Для реализации метода Гаусса используют встроенную функцию rref( ). Для этого вводят соотношение:

• 5.    Непосредственно треугольный вид расширенной матрицы на экран компьютера вызывается записью

TRM := rref (ROZSHM)

TRM =

При этом на мониторе отображается результат:

	" 1	0	0	1
TRM:=	0	1	0	0
	. 0	0	1	— 2

Понятно, что последний столбец содержит значения корней системы. Используя эту матрицу, можно записать систему, эквивалентную данной, в следующем виде:

x 1 + 0 x 2 + 0 x 3 = 1,

< 0Xj + x2 + 0x3 = 0, 0 Xj + 0 x2 + x2 = —2.

Откуда имеем: x = 1; x = 0; x = -2.

• 6.    Программно последний столбец расширенной матрицы (столбца решений) можно отделить при помощи встроенной функции submatrix ( A , ir , jr , ic , jc ). Такая функция формирует матрицу, которая является блоком матрицы А, расположенным в строках от ir до jr и в столбцах от ic до jc . Итак, отделим решение от расширенной матрицы при помощи функции submatrix (A, ir, jr, ic, jc) следующим образом:

• 7.    Результат решения системы уравнений на экран компьютера можно вывести при помощи обращения Х =

• 8.    Проверка решения выполняется при помощи обращения

Х := submatrix (TRM, 1, 3, 4, 4)

ГП

После чего там появляется решение

X= 0

А ■ Х - В =

На мониторе появляется

A • X - B = 0

Процесс решения изображен на рис.1.

Заметим, что в среде имеется стандартная функция rref( ) , которая может выполнять и прямой, и обратный ход метода Гаусса.

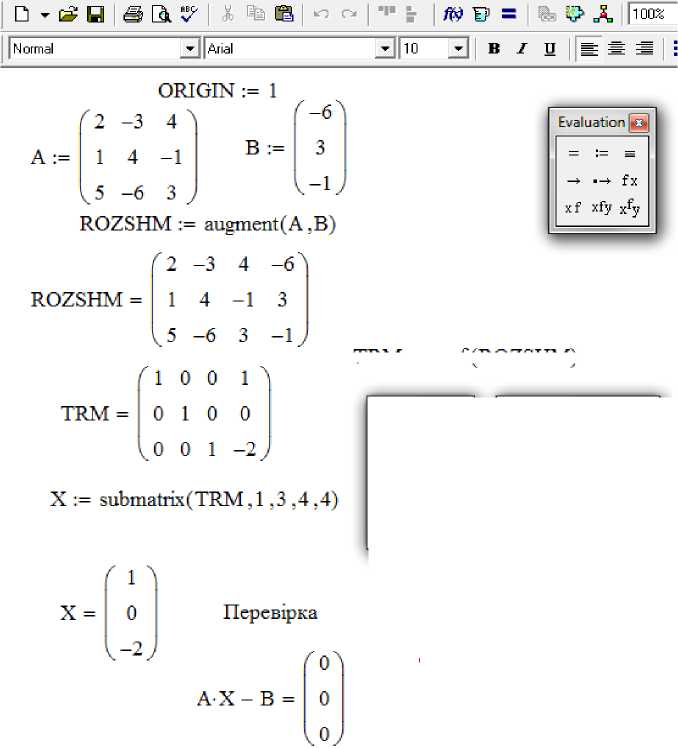
Рис. 1. Решение системы линейных алгебраических уравнений в среде Мathcad

TRM := rref(ROZSHM)

Заключение

В статье отражены далеко не все проблемы, с которыми пришлось столкнуться нашему образованию в постсоветский период. Для возвращения позиций, утерянных в пылу необдуманных «реформ», уже сейчас необходимо внедрять в учебный процесс новые технологии и инструменты, позволяющие стимулировать интерес к самостоятельной работе студентов, что в современных реалиях образовательного процесса приобретает решающую роль, т.к. в какой-то мере компенсирует уменьшение количества аудиторных занятий.

Авторы считают, что «параллельная» иллюстрация классического подхода и приемов, основанных на использовании IT-технологий, как «методический ход», заслуживает внимания при изучении большого числа фундаментальных и прикладных дисциплин.