Некоторые случаи силовой нагрузки в тазобедренном суставе человека при периодическом движении

Несмотря на многие исследования, проведенные в области гидродинамической теории смазки в тазобедренном суставе человека [1, 2, 7, 9–13, 17, 21, 26], неизотермические, неньютоновские свойства нестационарного течения синовиальной жидкости не были изучены должным образом. Не рассматривались случайные изменения поверхностей тазобедренного сустава человека.

Авторы работ [1, 7, 12] предоставили параметры, возникающие при работе тазобедренного сустава человека, с использованием численных и аналитических методов. В работах [9, 17, 21, 26] представлены новые методы вычисления силы трения для суставов человека с различными геометриями соприкасающихся поверхностей хряща и деформируемой высотой суставного зазора.

Периодическое движение головки и суставной впадины тазобедренного сустава с различными амплитудами и частотами было рассмотрено только К. Вежхольским [23, 24].

В настоящей статье автор проделал численные вычисления давления и нагруженности в зазоре тазобедренного сустава человека с помощью аналитических

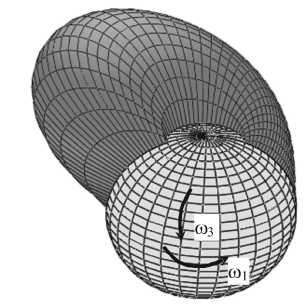
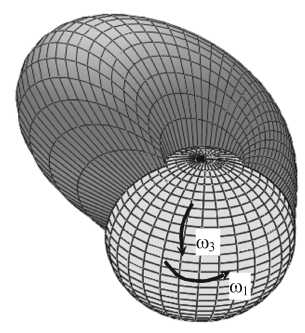
головка сустава 9 = п/8      головка сустава ф = о                           ф =п       /      / ^^^^^^^^^■~9= п/2 М|ЬЦ=й^ n Г а)

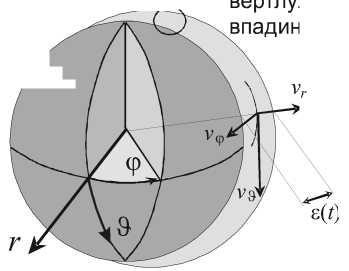
A     вертлужная A впадина v r \ Г ^АхХ      Ч J фхк/Ч XX  \  } / /v 9у        \   4 1/ х /             е( t )   X 7 (/ /

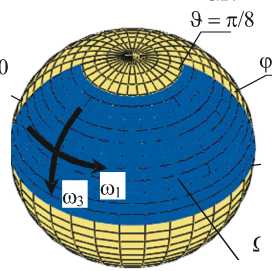
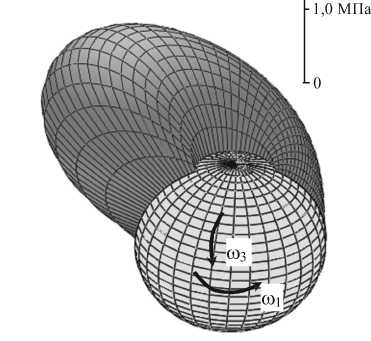
Рис.1. Схама рассматриваемой области Q

решений К. Вежхольского [24]. Вычисления сделаны для периодического смазывания вязкоупругой синовиальной жидкостью и случайных эффектов изменения хрящевых поверхностей (рис. 1б).

Сферическая головка сустава движется одновременно в окружном и меридиональном направлениях с различными угловыми скоростями, рис. 1а. Символ ф означает координату в окружном направлении, 9 - координата в меридиональном направлении, r представляет направление высоты зазора.

Новым результатом данной работы является численный анализ влияния частот возмущения и вязкоупругих свойств синовиальной жидкости на нагруженность тазобедренного сустава человека, учитываются случайные изменения шероховатости поверхности хряща.

Численные вычисления были проведены с помощью программы MathLab 7.1 на основе метод конечных разностей [5, 14, 15].

• 2.    Определяющие уравнения и деформация высоты зазора

  сустава человека и уравнениями порядка общего быть записаны в

  
  

Течение синовиальной жидкости в зазоре тазобедренного описывается уравнениями сохранения количества движения неразрывности. Эти уравнения и аппроксимация второго конститутивного уравнения, данного Ривлином-Эриксеном, могут следующей форме [5, 8, 19, 20, 22–24]:

Div S = p d v , div v = 0, S = - p I + p A, +a ( Aj )² + 0 A₂ , dt                                            ^{1          1           2}

где: S - тензор напряжений, p - давление, I - единичный тензор, A 1 и A ₂ - два первых тензора Ривлина-Эриксена и n , а , 0 - три материальных константы синовиальной жидкости, где n = n 1 n ₀ означает полную вязкость, n 1 - безразмерную вязкость, n ₀ -размерное значение вязкости. Тензоры A 1 и A 2 задаются симметричными матрицами, определенными в работах [8, 18, 23, 24]:

d v

A, = L + L T , A₂ г grad a + (grad a ) T + 2 L T L , a г Lv +    ,

1                    2                                                          d t где: L - тензор градиента вектора скорости жидкости, LT - тензор, задаваемый транспонированной матрицей градиента скорости синовиальной жидкости, v - вектор скорости, t - время, a - вектор ускорения.

Предполагается, что произведение чисел Деборы и Строухала, то есть DeStr, и произведение числа Рейнольдса, безразмерного зазора, и числа Строухала, то есть Re v Str, имеют одинаковый порядок величины. Кроме того, DeStr » De в m , п ₀ = в m 3 / п ₀, где m 1 - угловая скорость головки сустава в окружном направлении - , m 3 - угловая скорость головки сустава в меридиональном направлении 9 . В расчете приняты следующие допущения: течение синовиальной жидкости в зазоре – несимметричное и неустановившееся, свойства синовиальной жидкости – вязкоупругие и неустановившиеся, плотность р синовиальной жидкости - постоянная величина, отсутствие проскальзывания поверхностей кости. Кроме того, введены обозначения: £ 0 - характеристическое значение высоты зазора в тазобедренном суставе, R - радиус головки сустава, t 0 - характеристическое размерное значение времени [8, 22–24]. Зависимости между числом Рейнольдса, модифицированным числом Рейнольдса, числами Строухала и Деборы следующие:

Re Р^^ , Re ^.Wo., str = J_, De 3^ 1 , DeStr , Re _v Str ^1^ . (3) П о П о ^m i t o П о П о t o П о t o

Для синовиальной жидкости верно неравенство о <в / t о <П _о и коэффициент псевдовязкости в имеет значения в основном в диапазоне от 0,000001 до 0,01 Пас². Пренебрегая членами с радиальным зазором ^ = £ _о/ R * Ю^{- 3} в определяющих уравнениях в сферических координатах: - , r , 9 и учитывая выше упомянутые допущения, можно получить следующие соотношения [4, 8, 23]:

^d v ф 5 t

'       ■ "-fn

рRsinf®)6- PdrI 6r J ( R J

в dv-р 5t5 r2

+ O (De),

о      + O (De),                                  (5)

5 r

=- 1 - ^p +2k       V-^X + O (De),

dt     р d9 р 5r у 5r J р 5t5r

5vф

—^- + R sin

5ф

9)5 vr 5

—--1--

RJ 5r 59

_p f 9

R v sin

⁹ I R

= о,

d r

If 1

( 5 r J

⁺ П о П 1

2 d) 2 fd v ₃ ) — I + —⁹- d r J У 5 r J

+ O (De) = о,

где: 0 < - <  2 л0 1 , о < 0 1 <  1, п /8 <  ( 9 / R ) < п /2, о <  r < £ , £ - размерная полная высота зазора, к - теплопроводность синовиальной жидкости.

Члены, умноженные на коэффициент в, описывают вязкоупругие свойства синовиальной жидкости. Конвективные члены в уравнениях (4, 6) сохранения количества движения не учитываются. В уравнении энергии учтены только члены с теплопроводностью и с эффектом вязкой диссипации. В левой части уравнений для количества движения члены с ускорением учитываются.

Символы v _ф , v_r , v _— означают размерные компоненты скорости синовиальной жидкости в окружном, высоты зазора и меридиональном направлениях по отношению к головке сустава, соответственно.

Стохастическое уравнение Рейнольдса

Модифицированное уравнение Рейнольдса для стационарного течения синовиальной жидкости без вязкоупругих свойств, но с учетом случайных эффектов было получено К. Вежхольским [24] и имеет вид:

д {Е(a3)5E(p(0))!         f —Л 5 [Е(a3)5E(p(0)) , —

— < —-—-  ---- 1 + R sin I I—< —-—-  ---- sin —

5ф П0П1    дФ          V R Я$ П0П1    d— R

= 6 to 1 R ²

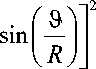
5E (a) бф

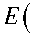
где Q: 0 < ф < п, пR/8 < — < пR/2.

Модифицированное уравнение Рейнольдса для коррекций давления p ^{( k )} , ( к = 1,2,...), вызванных периодическим течением синовиальной вязкоупругой жидкости и одновременно случайными эффектами, было получено К. Вежхольским [24] и имеет вид:

5 fE(a3) 5E(рJ1 2f . — 5 fE(a3) 5E(р) . — — < —1 + R21 sin— I—^ —sin — дф( Пka дф J V R Jd— I Пka d— R

= - 12 to o R ² B e

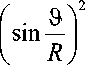
a ⁽⁰⁾ S.

sin ( к to ₀ 1 ) k ⁴

-

- 12 R l sin — If ^ фо S ф vk V R /

5E (a) 5ф

l —

⁺ R I sin^ I ^V — 0 ^S Э vk

V R J

5 E ( a )

5—

cos(k to01)

k3     +

l—V

+ 6 ^R V sin R j^ U _фД S ф uk

⁺ V pO ^S ф vk ]

faE(s).°s,ktot: + top; a:E(a,)Xnk] 5ф     k5      12k4 5фь         J

1 +

P_ck =^ e[Р ⁽ k ) exp( i k ю ₀ 1 )],

X

_ sin( k ю ₀ 1 ) ₊ cos( k ю ₀ 1 )

n k n ka

n kb

— 'J? e nka

< 1 A

¹   _ П0 П 1

v ⁿ k)   |n k |²

1           ( 1 )

— = ^ m — П kb      <П k )

k ю0вIП k Г ’

nk = П0П1 + ikЮ^,  |nk |2 = (П0П1 )2 + (kЮ0Р)2 •

Уравнение (10) определяет коррекции давления P ck , вызванные условиями нестационарного течения и свойствами вязкоупругой синовиальной жидкостью. Амплитуды колебаний на головке сустава U и на вертлужной впадине V и функции S изменений частот колебаний, входящие в уравнение (10), имеют следующий вид:

U фД ^_Ю 10 R sin ( ^Э / R ) , U ЭД ^{_ Ю} 30 R sin ф , ^V i 0 = ^COnSt , ^S imk = ^S imk ^{( Ю} т , ^k X ^S rk = ^S rk ^{( Ю} r ^),(12)

где г = ф , Э ; k = 1, 2, ..; m = и , v ; 0 <  Be <  1. Безразмерный коэффициент B e регулирует значения амплитуд для поперечных колебаний головки сустава.

Символы ю_ф v , ю_{ф и} , ю_Э v , ю_{Э и} означают переменные частоты колебаний в направлениях ф и Э на вертлужной впадине (нижний индекс v ) и на головке сустава (нижний индекс и ). Символ ю r есть частота колебаний в направлении высоты зазора, а символ ю ₀ описывает частоты возмущений для неустановившегося течения синовиальной жидкости в зазоре сустава.

Символы ю ₁ , ю ₁₀ означают угловые скорости и их возмущения для сферической головки бедра в окружном направлении ф . Угловые скорости и их возмущения для головки сустава в меридиональном направлении Э равны ю ₃ и ю ₃₀.

Функции S iuk , S ivk , S rk зависят от частот ю_ф v , ю_{ф и} , ю_Э v , ю_{Э и} , ю r и их точные изменения и зависимости описаны в работе [24]. В частном случае для Ю ф v = Ю ф и = Ю э v = Ю э и = ю r = ^ю 0 имеем S ^ uk = 1, S ₉ «k = 1, S q vk = 1, S s vk = 1, S rk = 1.

Уравнение (10) определяет ожидаемые значения коррекций давления E ( P_ck ). Ожидаемое значение полной величины давления и оператор ожидания E определяются в следующем виде [6, 8, 24, 25]:

^

E (Р ) = E (Р"’) + Ё E (Pck) • k=1

+^

E (*) = J ( • ) x f ( 6 ) d 6 , f ( 6 ) _<

-to

32 c ⁷

( c² -6 ² ) ³

при - c < 5 < + c, при |6| > 0,

где функция f есть функция плотности вероятности стохастических изменений шероховатых неровностей на поверхности хряща [16]. Символ с означает половину общего диапазона изменяемости случайной переменной ( * ). Ожидаемая величина из высоты зазора и из третьей степени высоты зазора имеет вид [6, 24]:

+to                                            +to

E(е) = j Еf(6)d6 = Г,,: ,E(e3) = J e3f (6)d6 = (Г,E(0-) (1 + 3p2),0

Г ,E            3

Безразмерный коэффициент 0 < p <  1 описывает случайные эффекты. При р = 0 случайные эффекты отсутствуют. Значение c = ± 3 с ограничивает область функции f, где с - размерная дисперсия.

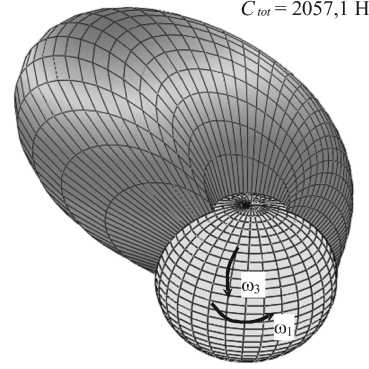
t = 0 и t = 2 п/« ₀ с p max = 1,757 10⁶ Па

C to t = 1177,4 Н

t = л/« ₀ с

t = 0,3 п/« 0 с p max = 2,001 10⁶ Па

C to t = 1378,5 Н

2,0 МПа

1,0 МПа

p = 1,676 10⁶ Па max

C to t = 1173,5 Н

Рис. 2. Распределения давления в зазоре тазобедренного сустава в выбранные моменты времени, R = 0,0265 м, п = 0,15 Пас, « 1 = 2,0 с ^{- 1}, « 3 = -0,6 с ^{- 1}, « ₁₀ = 0,25 с ^{- 1}, « ₃₀ = 0,05 с ^{- 1}, « ₀ = 10 с ^{- 1}, р ₀= 0,001 Пас², р = 1/3, Q = 20,38 см²

2,0 МПа

1,0 МПа

t = 1,7я/« 0 с pmax= 1,474 106 Па

C to t = 957,8 Н

Общая величина нагруженности определяется из следующей формулы [8, 24]:

C tot = J E [ p ( ф , Э )] d П ( ф , Э ),                           (15)

П ( ф, Э )

где символ J означает поверхностный интеграл, заданный на всей поверхности

Q головки сустава.

Для численных вычислений используются следующие выражения для высоты зазора сустава:

в(0) (ф, R) = Ав x cos ф sin (-Э) + Ав y sin ф sin (f) - Ав z cos (f) - R +

⁺ { [ ^Ав x cos ф sin (f ) + ^Ав y sin ф sin ( R ) - ^Ав _z COS (f) ] ² + ( R + ^в min ) ( R + ² D + ^в min ) } ² ,      ⁽¹⁶⁾

t = 0 и t = 2 n^zw ₀ с p max = 1,895 10⁶ Па

C to t = 1241,3 Н

2,0 МПа

t = 0,3п/ю0 с p max= 2,888 106 Па

1,0 МПа

t = 1,7л/« 0 с p max= 0,728 106 Па

C to t = 333,0 Н

t = п/« 0 с pmax= 1,585 106 Па

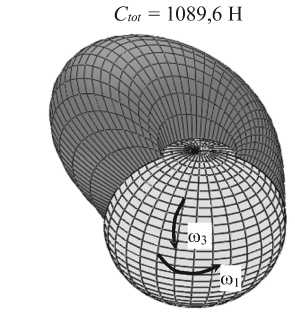
Рис. 3. Распределения давления в зазоре тазобедренного сустава в выбранные моменты времени, R = 0,0265 м, п = 0,15 Пас, га = 2,0 с ^{- 1}, га ₃ = -0,6 с ^{- 1}, га₀ = 0,25 с ^{- 1}, « ₃₀ = 0,05 с ^{- 1}, ® 0 = 100 с ^{- 1}, 0 0 = 0,001 Пас², р = 1/3, Q = 20,38 см²

2,0 МПа

1,0 МПа

где D = ( As 2 + As 2 + As 2 ) ² - эксцентриситет.

При отклонении высоты зазора сустава было предположено, что центр сферической головки сустава расположен в точке O (0,0,0) и центр вертлужной впадины фиксирован в точке O ₁( x -As _x , y -As _y , z + As _x ), где эксцентриситет имеет значение D .

• 4.    Численные вычисления

  Распределение давления p ⁽⁰⁾ и его коррекции p ⁽¹⁾, p ⁽²⁾,...определяются внутри области смазывания Q (см. рис. 1а). На границе области Q величина полного давления равна атмосферному давлению p at . Численные вычисления в области Q производятся для следующих величин: R = 0,0265 м, ю ₁ = 2 с ^{- 1}, ю ₃ = - 0,6 с ^{- 1}, ю ₁₀ = 0,25 с ^{- 1}, © ₃₀ = 0,05 с ^{- 1}, As _x = 2,5 мкм, As _y = 0,5 мкм, As _z = 2,0 мкм, n o = 0,06 Пас, р₀ = 1000 кг/м³.

2,0 МПа

t = 0 и t = 2 п/ю ₀ с p max = 1,756 10⁶ Па

C to t = 1176,9 Н

1,0 МПа t = п/ю0 с pmax= 1,676 106 Па

C to t = 1137,9 Н

t = 0,3п/ю0 с p max= 1,994 106 Па

C to t = 1373,3 Н

2,0 МПа

t = 1,7п/юо с p max= 1,479 106 Па

C to t = 962,5 Н

1,0 МПа

Рис. 4. Распределения давления в зазоре тазобедренного сустава в выбранные моменты времени, R = 0,0265 м, п = 0,15 Пас, ю 1 = 2,0 с ^{- 1}, ю ₃ = -0,6 с ^{- 1}, ю ₁₀ = 0,25 с ^{- 1}, ю ₃₀ = 0,05 с ^{- 1}, Ю о = 50 с ^{- 1}, Р 0 = 0,0001 Пас², р = 1/3, Q = 20,38 см²

Наименьшее значение высоты зазора сустава равно £ _min = 3,6 мкм, а максимальное значение высоты зазора сустава s _max = 9,3 мкм. На первом шаге численных вычислений коэффициент псевдовязкости предполагается постоянным: р ₀ = 0,001 Пас², однако частоты возмущений течения имеют следующие размерные значения: ю ₀ = 10 с ^{- 1}, ю ₀ = 20 с ^{- 1}, ю ₀= 50 с ^{- 1}, ю ₀= 100 с ^{- 1}. Одновременно, безразмерный коэффициент возмущений высоты зазора сустава изменяется следующим образом: B e = +0,01, B e = +0,005, B e = +0,002, B e = +0,001. На втором шаге вычислений были предположены: постоянное значение частоты возмущений ю ₀ = 50 с ^{- 1}, безразмерный коэффициент возмущений высоты зазора B e = +0,002, а также из различных значений коэффициентов псевдовязкости в диапазоне от р ₀ = 0,0001 Пас² до р ₀ = 0,0024 Пас² было выбрано значение 0,0005 Пас².

При численных вычислениях были предположены одинаковые значения изменений частот течения в окружном, меридиональном и радиальном направлениях на вертлужной впадине и головке сустава, то есть «„ = юфu = юа„ = ю9u = юr = ю0. Поэтому t = 0 и t = 2п/® 0 с pmax= 1,961 106 Па

t = 0,3п/®0 с p max= 3,283 106 Па

C to t = 2358,7 Н

C to t = 1269,7 Н

2,0 МПа

2,0 МПа

t = 1,7л/® о с p max= 0,407 106 Па

C to t = 55,3 Н

t = п® с pmax= 1,550 106 Па

C to t = 1068,4 Н

Рис. 5. Распределения давления в зазоре тазобедренного сустава в выбранные моменты времени, R = 0,0265 м, п = 0,15 Пас, ® ₁ = 2,0 с ^{- 1}, ® ₃ = -0,6 с ^{- 1}, ® ₁₀ = 0,25 с ^{- 1}, ® ₃₀ = 0,05 с ^{- 1}, ® ₀ = 50 с ^{- 1}, р ₀= 0,0024 Пас², р = 1/3, Q = 20,38 см²

1,0 МПа

функции изменений частот, встречающихся в модифицированном уравнении Рейнольдса (10), следующие: S _ф uk = 1, S з uk = 1, S _Ф vk = 1, S з vk = 1, S rk = 1. В численных вычислениях предположены следующие не зависящие от времени изменения амплитуды и тангенциальных скоростей на вертлужной впадине, а именно: V _р о = 0,001 м/с, V _{3 0} = 0.0002 м/с. При всех численных вычислениях был предположен безразмерный коэффициент р = 1/3 случайных эффектов изменений высоты зазора.

На рис. 2, 3, 4, 5 представлены распределения гидродинамического давления, полученные с помощью модифицированных уравнений Рейнольдса (9, 10) для выбранных моментов времени в течение периодов возмущений. Полное значение периода возмущений равно t = 2 п / ® ₀.

На рис. 2 показаны зависящие от времени распределения давления в сферическом зазоре тазобедренного сустава человека при параметрах: р = 1/3, р 0 = 0,001 Пас², ® 0 = 10 с ^{- 1}, B e = +0,01.

Соответствующие значения параметров для других рисунков:

рис. 3, р = 1/3, р 0 = 0,001 Пас², ® 0 = 100 с ^{- 1}, B e = +0,001;

А

Мищак. Некоторые случаи силовой нагрузки в тазобедренном суставе человека при движении.

Нагрузка C _tot , Н                                                Нагрузка C _{to t} , Н

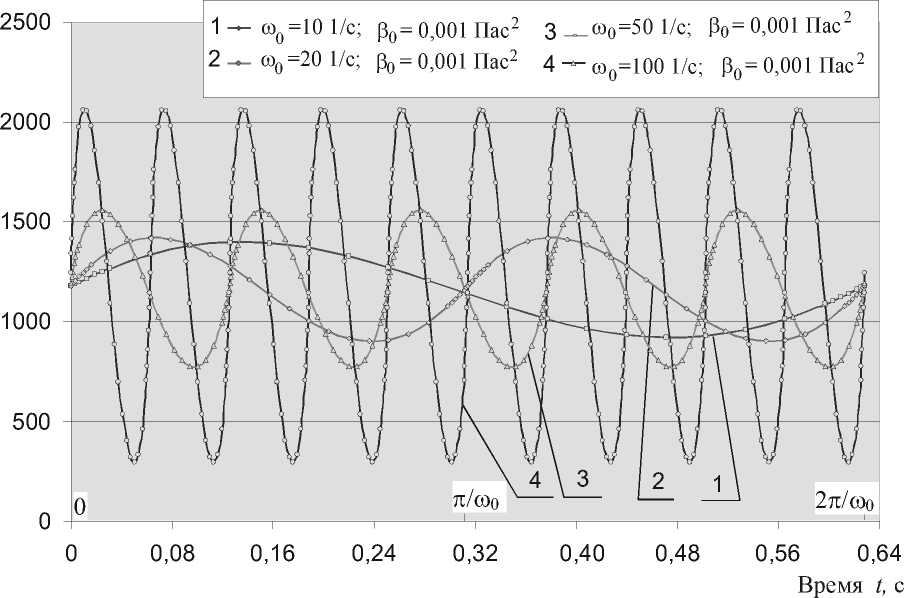
Рис. 6. Изменения нагруженности в зависимости от частоты возмущений течения ю 0 при постоянном значении коэффициента псевдовязкости р ₀ = 0,001 Пас²

Ю₀=50 1/c

1 A P c = 0,0001 Пас ² 4 - -Pg = 0,0015 Пас ² 2 — о—р ₀ = 0,0005 Пас² 5 _д р ₀ = 0,0020 Пас² 3 --в = 0,0010 Пас ² 6 ж р 0 = 0,0024 Пас ²

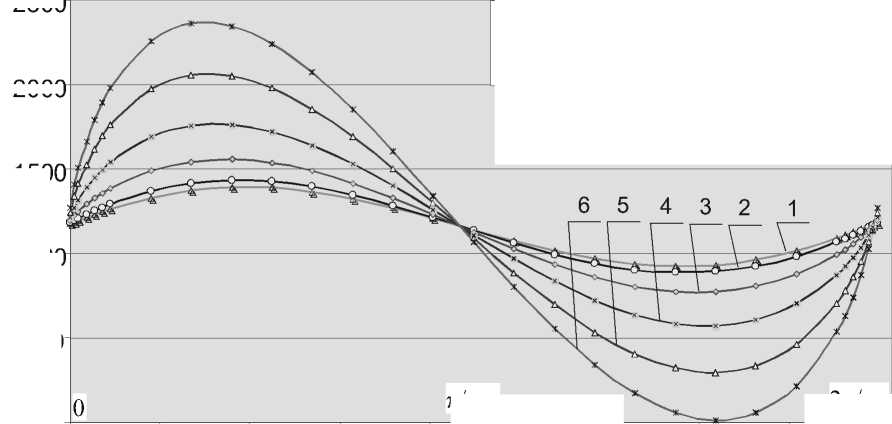
2n/too n/to0

0    0,014 0,028 0,042 0,056  0,070 0,084 0,098 0,112 0,126

Время t , c

Рис. 7. Изменения нагруженности в зависимости от коэффициента псевдовязкости р ₀ для постоянного значения частоты возмущений течения ю 0 = 50 с ^{- 1}

рис. 4, р = 1/3, в о = 0,0001 Пас², to o = 50 с ^{- 1}, B e = +0,002; рис. 5, р = 1/3, в о = 0,0024 Пас², to o = 50 с ^{- 1}, B e = +0,002.

Изменения нагруженности в зависимости от частоты возмущений течения ω 0 при постоянном значении коэффициента псевдовязкости β 0 = 0,001 Пас² представлены на рис. 6. Изменения нагруженности в зависимости от коэффициента псевдовязкости β 0 для постоянного значения частоты возмущений течения ω 0 = 50 с ^{- 1} представлены на рис. 7.

• 5.    Заключение

Из численных вычислений следует, что увеличение частот возмущений течения в зазоре тазобедренного сустава при постоянном значении коэффициента псевдовязкости вязкоупругих свойств вызывает заметное увеличение нагруженности. Вязкоупругие свойства синовиальной жидкости имеют большее влияние на нагруженность при больших частотах возмущения, чем при малых возмущениях. Если рассматриваемая частота возмущения постоянна, но значение коэффициента псевдовязкости меняется, то получаем видимые изменения максимального и минимального значения нагруженности сустава в течение рассматриваемого периода возмущений. Если величины коэффициента псевдовязкости увеличиваются, то значение нагруженности сустава увеличивается в течение первой половины периода возмущения и убывает в течение второй части периода возмущений.

Стохастические изменения высоты зазора сустава, вызванные шероховатостью поверхностей хряща, уменьшают значения нагруженности на 9-12 %.

Детальный численный анализ влияния частот возмущения течения и свойств вязкоупругой жидкости на значения нагруженности сустава при неустановившемся периодическом движении смазки позволяет учесть соответствующие параметры движения при реабилитации пациентов после травм тазобедренного сустава и при тренировке спортсменов.

Благодарности

Данная работа была профинансирована фондом KBN в течение 2003-2006 годов как научный проект KBN 411E–030–25.