Некоторые способы вычисления параметров криволинейного равноускоренного движения

Равноускоренным движением, как известно, называется такое движение жёсткой системы отсчёта, при котором компоненты собственного ускорения её начала остаются постоянными. При этом такая система отсчёта не вращается относительно мгновенно сопутствующей инерциальной системы отсчёта. Иногда [1, с. 128, п. 19] под таким движением понимается движение под действием силы, остающейся постоянной в лабораторной системе. Но в том случае, если система отсчёта под действием силы двигается не прямолинейно и постольку, поскольку в процессе движения направление скорости системы отсчёта изменяется относительно осей лабораторной системы S*, то вследствие тензорного закона преобразования 3-сил, сила в собственной системе отсчёта будет изменяться как по величине, так и по направлению. Поэтому в общем случае такое движение нельзя рассматривать как равноускоренное. Это движение - под действием однородного силового поля в лабораторной системе отсчёта здесь будет называться гиперболическим. Различие между этими двумя типами движений системы отсчёта s видно ещё и по тому, что для гиперболического движения в системе S* обычно несущественна собственная ориентация s, поэтому оно полностью определяется начальной скоростью s. Равноускоренное же движение s характеризуется, кроме начальной скорости ещё и 3 углами, определяющими начальную ориентацию s относительно S*. Таким образом, следует различать равноускоренное и гиперболическое движения. Только в том случае, когда гиперболическое движение и равноускоренное движение разных систем отсчёта осуществляется вдоль одной прямой линии, скорости их начал отсчёта как функции лабораторного времени будут друг с другом совпадать.²

Цели данной статьи две.

Ранее в [2, формулы (2.10), (2.11)] были представлены так называемые ^пуравнения обратной задачи кинематики^п, то есть дифференциальные уравнения для параметров движения неинерци-алыюй системы отсчёта: 3-вектора v‘ и матрицы поворота а@в ・ С другой стороны давно известно уравнение движения для ортонормированной тетрады 4-векторов, ассоциированных с данной системой отсчёта [3, формула (4)] (см. также [4, формулы (5.3), (5.4)]). Все эти уравнения являются следствием (см. [2], [5, формулы (15), (16)]) известного преобразования Лоренца-Мёллера-Нэлсона в произвольную жёсткую систему отсчёта и, следовательно, эквивалентны друг другу. Тем не менее, на практике данные уравнения почти не использовались (см. впрочем [6], [7]) и, поэтому, они всё ещё недостаточно обоснованы. Таким образом, одна из целей статьи заключается в проверке данных уравнений на примере наиболее общего равноускоренного движения. Причиной для применения в качестве теста именно равноускоренного движения, являются математические трудности при решении общих дифференциальных уравнений обратной задачи кинематики.

Кроме того, общее (не обязательно прямолинейное) равноускоренное движение интересно само по себе. На практике движение равноускоренной системы отсчёта может встретиться в будущем в космонавтике, так как космические станции, совершая перелёты, будут представлять собой системы с постоянным собственным ускорением. Задача о равноускоренном движении применяется, например, при изучении электромагнитного излучения заряда. Вследствие своей важности равноускоренное движение рассматривалось на самых ранних этапах развития теории относительности. Пионерской работой, в которой было получено правильное релятивистское преобразование в прямолинейно движущуюся равноускоренную систему отсчёта является [8]. Затем, исходя из различных исходных предположений, предпринималось множество попыток рассматривать общее преобразование в равноускоренную систему отсчёта. Однако следует признать, что общее преобразование в равноускоренную систему в явном виде по какой-то причине не записано. Поэтому другая цель статьи заключается в том, чтобы без каких либо упрощений и предположений получить в явном виде, с точностью до произвольного поворота, преобразование в криволинейно движущуюся относительно лабораторной системы отсчёта S* равноускоренную систему отсчёта s.

Статья построена следующим образом.

В первом параграфе данной статьи даются предварительные сведения касающиеся поведения параметров преобразования Лоренца-Мёллера-Нэлсона при совершении буста. В п. 2 общее равноускоренное движение и все его параметры получаются простым лоренцевским бустом из первоначального прямолинейного равноускоренного движения. Вследствие своей наглядности, параметры общего равноускоренного движения полученные бустом будут служить образцом для сверки с двумя другими способами определения равноускоренного движения. Один из этих способов заключается в прямом решении в п. 4 уравнений обратной задачи кинематики, а второй (в п. 5) -в решении уравнений движения тетрады. Сверка решений, полученных всеми этими способами осуществяется в п. 6. Наконец, в п. 7 находится общее преобразование в равноускоренную жёсткую систему отсчёта. Кроме того, в третьем параграфе будет проверено одно утверждение статьи [4] о взаимной компенсации вращения Вигнера и прецессии Томаса для равноускоренного движения системы s -

1. Изменение специального преобразования Лоренца-Мёллера-Нэлсона при бусте

Напомним как изменяется при бусте так называемое специальное преобразование Лоренца-

Мёллера-Нэлсона (здесь и далее c = 1) из лабораторной системы отсчёта S : (T, R) в неинерциаль- ную, радиально жёсткую систему отсчёта s : (t, r), которая движется произвольно «без поворота»

от носите лыю S [9]

vr t

= vr-v2 + /

dt

\/1 - v2

(1.1)

R = r +

1 - “ 一 V ： v² ， 1 — V²

2t

-^{(vr ) v} + 厶

vdt

Х/1 — V2

(1-2)

Совершим переход из системы отсчёта S в движущуюся с постояпиой скоростью u относительно неё инерциальную систему отсчёта S * : (T *, R*). Координаты и врем я в системах отсчёта S, S* связаны обычным преобразованием Лоренца

T -uR

(1.3)

Х/1 — u² ，

R* = R+¹ив u- 二

.

(1-4)

Оказывается, что системы отсчёта Нэлсона вида

S* ii s связаны обшіім преобразоватшем Лореіш.а-Мёллер а-

где

Ra

T* _ va aear/3 + /'    dt V1 — V*2 丿0 V1 - aea% + 1 — V1 — V*2 v*2V1 — V*2 ■ Va vy ав Y rp „ * vi - u2v - u (1 — V1 — u2)(uv)u

+/ 0

't va 必

V1 — V*² ，

v

1 — uv

(1.5)

(1.6)

u2(1 — uv)

.

v — ,1 — V² u    (1 — ,1 — V² )( uv ) v

(1.8)

1 — uv           v²(1 — uv )

Матрица поворота ава в координатах: ось поворота n , угол поворота ф имеет вид ава = 8ав cos фw + n"na(1 — cos фw) — еавүnY sin фw .                  (1.9)

Угол поворота, который получил название поворота Вигнера и соответствует матрице a/a равен n sin фw

________ u X v ________ (1 _— (1 - у!

1 + ,1 — V²,1 — u² — uv 、

—u2)(1 — ,1 — V2)

u2v2

uv ,

(1.10)

cos фw

1 + V1 - u² V1 - V² - uv

,

(1-11)

n tg 萼

sin фw

u 义 v

n----------- — = -------- ,       - 、 ---------- ,       - 、 --------

1 + cos фw (1 + 71 — u²) (1 + V1 — V²) — uv

,

(1-12)

где1 n есть едііішчпып вектор в направлении поворота.

2. Определение параметров равноускоренного движения с помощью буста

Поставим задачу следующим образом. Предварительно выберем собственную ориентацию равноускоренной системы отсчёта s : (t, r) так, чтобы её собственное ускорение было направлено вдоль оси 1. Пусть в начальный момент времени равноускоренная система отсчёта s : (t, r) в некоторой лабораторной системе отсчёта S : (T, R ) находилась в покое и полиостью совпадала с S. Далее она от носите лыю S движется прямолпиепио с собственным ускорением W в положительном направлении оси 1. В этом случае равноускоренное движение хорошо известно. Скорость её начала равна Vi = th Wt [10. с. 207. (формула (8.1G8)]. Перейдём теперь из системы S в иовуто пиерипальпуто систему отсчёта S* : (T*, R *), которая двигается в плоскости осей 1 и 3 со скоростью u = (ui, 0, из). При таком бусте у системы s в новой системе отсчёта появляются начальные компоненты скорости вдоль осей 1 и 3. Следовательно движение системы s в системе отсчёта S*, которую можно принять за лабораторную систему, будет общим равноускоренным движением. Требуется только определить новые параметры движения s в S*.

Зная теперь формулы (1.7)-(1.12) нетрудно найти параметры криволинейного равноускоренного движения. Согласно формуле (1.7) новая скорость s относительно S* будет равна (греческие индексы у компонент векторов будем писать внизу, чтобы отличать их от показателей степени)

V1*

,1 — u2 thWt — ui   (1 — ,1 — u2) u1 thWt

1 — uithWt    +   u2(1 — uithWt)

(2.1)

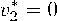
⑵ 2)

1 — uithWt*     u2(1 — uithWt)

(2.3)

Эта же скорость выраженная в системе координат s равна согласно (1.8)

Vi — ui    thWt — ui

1 — uiVi 1 — ui thWt

(2-4)

,* — — %/1 - v² U3 —__ U3_______

³      1 — uivi      chWt — ui shWt

При этом vα = aβαvβ , а матрица вращения Вигнера системы s относительно S* равна

cos φW 0 sin φW

0 — sin фw

0 cosφW

(2.6)

(2.7)

(2.8)

Поворот Вигнера, который необходимо сделать при бусте между системой координат s и системой координат, которая двигается «без поворота» относительно S осуществляется в плоскости осей 1 и 3 в направлении 3 т 1 . Согласно (1.10)-(1.12) угол этого поворота удовлетворяет равенствам

из [ shWt — MP2 ui (chWt — 1)] sin φW = chWt — ui shWt + %/1 — u2

(2-9)

cos φW

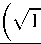
— u² +

l-u² ui) chWt — u1 shWt + 1 —

1-"1-u² u²

chWt — ui shWt + 封 1 — u²

(2.10)

φW tg 2

u3 shWt

( 1 + \/1 — u²)(1 + chWt) — ui shWt

(2.11)

Отсюда видно, что начальный угол ориентации равноускоренной системы, полученной бустом из (2.11) равен нулю. Вычислением векторов v* и угла Вигнера фw равноускоренное движение полностью задано. Параметры равноускоренного движения, полученные таким способом могут служить образцом для сравнения с другими решениями.

• 3.    Взаимная компенсация прецессии Томаса и вращения Вигнера в случае равноускоренного движения

Поскольку равноускоренное движение не обладает собственным вращением, то вращение Вигнера и прецессия Томаса должны компенсировать друг друга. Покажем это прямым расчётом. Угловую скорость вращения Вигнера можно получить дифференцируя уравнение (2.9). Получим

ωW cos φW

Wu3

— u² + ^{i -}4-u² ui) chWt — u_ishWt + 1 —

守 ui]

[chWt — uishWt + %/1 — u² ]

Поделив это выражение на (2.10) получим

Wu3

ωW =                        .

chWt — uishWt + %/1 — u²

Вычислим сейчас угловую скорость прецессии Томаса Q t

1 一 "] 一 .* 2 Q t = — V     v* X V*

v^*2 1 — v^*2

.Первый множитель в её определении будет равен

1 — , 1 — v*²       1         [chWt — uishWt] ²

---    -=—--------------- v*2 %/1 — v*2    %/1 — u2 chWt — uishWt + %/1 — u2

Дифференцируя параметр скорости получим

.*       W , 1 - u² Г     ( 1 — , 1 - u²) u ；

"vi                              О 1 —               Q              ,

(chWt — u_ishWt)            ^u

(3.1)

(3.2)

(3.3)

^v* = ⁰ , \/1 — u² (1 — \/1 — u²)

(3.5)

u2

•

Wu1u3

(ch Wt — uishWt)²

(3.6)

Второй множитель является векторным произведением и равен учитывая (2.1)- (2.3), (3.4)- (3.6)

/ *..•*、         * ♦ *       * ♦ *

( v 义 v ) 2 = V3V] — V*V3

W %/1 — u² U3 (chWt — uishWt)²

(3.7)

Следовательно перемножая (3.3) и (3.7) получим, что прецессия Томаса равна

От

Wu3

chWt — uishWt + %/1 — u²

.

(3.8)

Сравнивая формулы (3.1) и (3.8) видно, что в сумме собственная прецессия Томаса и собственное вращение Вигнера системы s дают нуль как это и должно быть.

• 4.    Определение параметров движения решением уравнений обратной задачи кинематики

Рассмотрим теперь применение дифференциальных уравнений обратной задачи кинематики [2] к криволинейному равноускоренному движению

W ’ = const , Q ’ = 0 .

(4.1)

С учётом этого условия, дифференциальные уравнения обратной задачи кинематики [2, формулы (2.10), (2.11)] принимают вид

’

V ’ = 箒 = W ’ — ( W ’ v ’) v ’ ,

(4.2)

3’

V ， ²

’2

:-----v ’ X W ’ .

(4.3)

Согласно п. 2 выберем ось 1 лабораторной системы отсчёта S вдоль вектор а ускорения W’ системы s. а ось 3 — лежаш.ей в её плоскости траектории, ^'ра.вііеіше (4.2) для оси 1 есть

V] = W (1 — v]2).

Интегрируя это уравнение получим v’i(t) = th(Wt + k),

(4.4)

где thk = v’i(0).

Проецируя уравнение (4.2) на ось 3 перпендикулярную ускорению получим с учётом (4.4), что v’3 + W th (Wt + k) v’3 = 0 .

Отсюда

v’3(t)= v’3(0)

ch к

ch (Wt + к),

(4.5)

V’² 二 v]2 + V3² 二 ”喘 Ws+Wt + ^{k )} ， L

J1 — v’²(0) chk ch(Wt + k)

.

Подставляя эти значения в выражение (4.3) получим, что единственная ненулевая компонента вектора ， 3 ， есть

^ ， 2W = Фw

V’2

v%W

Wv3(0) chk

ch(Wt + k) + J1 — v’3(0) ch²k

(4.6)

Интегрируя это выражение получим, что eWt+k + ,1 — v[(0)chk фW=2arctg —vfe— ek + л/1 — v’2(0)chk

— 2 arctg-----—-----³--+ a .

v3(0)ch2k

• 5.    Определение параметров движения

решением уравнений движения тетрады 4-векторов

Равноускоренное движение можно также определить сразу в 4-мерном виде, решая уравнения движения тетрады единичных 4-векторов связанных с началом равноускоренной системы s [3, формула (4)], [4, формулы (5.3), (5.4)]

dAai dt

dA°i dt

W аЛаі

W aA0i + еавү QY Aei

(5.1)

(5.2)

при условиях ортонормированности

A0iA0 i = 1,

A0iAai = 0,

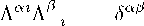
(5.3)

Четыре 4-вектора обладают 16 компонентами, которые входят в 16 уравнений (5.1), (5.2). Данные компоненты связаны друг с другом 1+3+6=10 условиями (5.3). Таким образом всего имеется 16-10=6 независимых величин, для которых можно записать 16-10=6 независимых уравнений, так, что данные уравнения допускают решение. Хотя в общем случае уравнения (5.1), (5.2) не проще уравнений обратной задачи кинематики, но для равноускоренной системы отсчёта они серьёзно упрощаются и допускают быстрое решение. Идея воспользоваться данными уравнениями принадлежит Фридману и Скарру [6], [7].

Учитывая (4.1) продифференцируем (5.1) по t и подставим в получившееся выражение значение (5.2). Получим, что

d 2 Aoi dt 2

W2Aoi,

(5.4)

Решение данного уравнения с учётом первого из уравнений (5.3) есть

A0i = Ai shWt + Bi chWt,

(5.5)

Ai Ai = —1, Ai Bi = 0, BiBi = 1.

(5.6)

Далее, равноускоренную систему координат выбираем согласно п. 2 так, чтобы собственное ускорение было направлено вдоль оси 1. Продифференцируем теперь с учётом (5.1) решение (5.5) по t. Получим, что первый 4-вектор равен

A1i = Bi shWt + Ai chWt.

(5.7)

Уравнения для остальных 4-векторов тривиальны

dA2i    dA3i

—■— = —■— dt      dt

(5.8)

Постоянные 4-векторы Ai, Bi, A2i, A3i определяются из того условия, что 4-вектора A0i , Aai как функции времени t должны иметь следующий вид [4, формулы (2.1), (2.2)] (индексы пишем внизу)

A0i = (A00, A0a) = ( "1— V*2 , ТТ-^),

(5.9)

Л г к     к \    ( ^VY a^aY -    , ^{1 —} Т¹ - ^v*2 一宀 .*_ \

^Aai = ^(Aa0^{, Aae}) = [ " 1- v*2 ^, a^ae + /" ] - v*2 vev"a^a" 丿 .

(5.10)

Учитывая эти равенства и то, что в начальный момент времени vi = —ui, V3 = —U3, а угол поворота равноускоренной системы относительно лабораторной системы отсчёта равен нулю, легко заметить, что ui        1 — "1 — u2 2   1 — "1 — u2

A = ^— Л——2 J + 2 /І——^ u1^,0, 2 「 \——^ u1u3 ^,            (5 ・ ^П)

1 — u2      u2 1 — u2 u2 1 — u2

Bi =(

"1 — u2

ui    0 _—    u3

"1 — u2 , , "1 — u2

Λ2i=(0,0,1,0) ,

.

(5.13)

(5.14)

u 1 - √1 - u2           1 - √1 - u2

Λ3i = -     3   ,              u1u3, 0, 1+

√1 - u2 u2√1 - u2             u2√1 - u2

• 6.    Эквивалентность данных способов определения равноускоренного движения

Сравним теперь решения (4.4), (4.5) с уже известными соответственно (2.4), (2.6). Нетрудно заметить, что эти решения совпадают (как это и должно быть) при следующем выборе постоянных k = - arth u1 , v‘3(0) = - из .

(6.1)

(6.2)

Можно также убедиться в тождественности (4.6) и (3.1) при условиях (6.1), (6.2). Следовательно и интегрирование (4.6) приводит с точностью до постоянной а в (4.7), определяющей начальную ориентацию системы s относительно S*, к вигиеровскому углу (2.9)-(2.11). Таким образом два решения, определяющих равноускоренное движение: с помощью буста и с помощью решения уравнений обратной задачи кинематики полностью совпадают.

Покажем, что способы определения равноускоренного движения с помощью буста и с помощью решения уравнений движения тетрады эквивалентны. Для этого вычислим сначала те компоненты 4-скорости начала отсчёта (5.9) и 4-векторов единичных ортов (5.10), расчёт которых не представляет трудности. Подставляя (2.1)-(2.3) в (5.9) и (5.10) получим, что

Λ00

chWt - u1 shWt

,         V；              1 — 7、- u2Ui ,

Λ01 =    1   = 1+           u21 shWt-chW

7i — V ； ²          u²7i — u²             71 — u²

Λ02 =Λ20 =   v2=0 ,

V1 - V * ²

.        V*       1 — 7l — U2,… U3

Λ03 = √ 3    =   √      · u1u3 shWt - √     chWt ,

1 — V * ²    u² 1 — u²                   1 — u²

Λ10

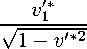
shWt - u1chW t ^√1 - u²

Λ30

■3*    — _—    u3

71 — V ‘* 2     71 — u²

Λ12 =Λ21 =Λ32 =Λ23 =0,

Λ22 =1,

Чтобы посчитать оставшиеся компоненты 4-векторов введём величины

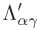
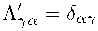
1 —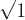— V ’* ²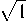

V ，* 2_— v ’*2

喧 ^VY * ,

тогда

Лав = аүв AYa

Вычислим коэффициенты А[ү учитывая (2.4)-(2.6). Получим

1         (shW t - u chW t)2

A1i =1+ ,---------------- /

1 - u2 chWt- u1shWt + 1 - u2

A33 = 1 +      ..1——

1 - u2 chWt- u1shWt + 1 - u2

(6.3)

(6.4)

(6.5)

(6.6)

(6.7)

(6.8)

(6.9)

(6.10)

(6.11)

(6.12)

(6.13)

Л1з

u3

√1 - u2

shWt - u1chWt chWt - u1 shWt + √1 - u2

(6.15)

Следующие четыре равенства не столь очевидны. Заменяя cos фw и sin фw их значениями из (2.9), (2.10) и зная равенства (6.13)-(6.15) можно доказать, что

Ли = аүі А ； 1 = an А] + a31A3i = cos фw A] + sin фwЛ31

= (l + -—— У u *] chWt-- u¹ shWt,                 (6.16)

u2√1 - u2             √1 - u2

• -               -/             . /13          ■/            . ,    ■ ，              , . , T 1 — 7\ — u² 2             ， . 一

^A33 = ^аү3^Аү3 = ^a13^A  + a33^A33 = — sin ^фW^A13 + ^{cos ф}W^A33 = ¹ +    ~~г     尸 ^u3 ,     (6 一 L ,)

u2 1 - u2

A13 = @ ү3А ； 1 = 。 13 八 11 + 。 33 八 31 = — sin Фw A11 + cos фw A ； 1 =

1 - √1 - u2                u3

=    -/[     2 一 U1U3 ch Wt — /[     - shWt,                         (6.18)

u2 1 - u2                 1 - u2

A31 = аү 1 A ； 3 = an A 。 + a31A33 = cos фw A\ + sin фw A33

1 - √1 - u2

u1 u3 .

u2√1 - u2

(6.19)

Доказательство равенств (6.16)-(6.19) заключается в аккуратном умножении данных уравнений на (chWt — U1shWt + vT—u²)². раскрытии скобок ii приведении подобных членов.

Сравнивая теперь (5.5), (5.7), (5.11)-(5.14) с (6.3)-(6.10) и (6.16)-(6.19) можно убедиться, что способы определения равноускоренной системы отсчёта с помощью буста и с помощью решения уравнения движения тетрады эквивалентны друг другу.

• 7.    Преобразование в равноускоренную систему отсчёта в явном виде

Общее преобразование Лоренца-Мёллера-Нэлсона в 4-мерной форме записывается в виде

T = Aaora +

0 Λ00dt,

Re = Aae ra + / Aoe dt.

(7.1)

Подставляя 4-векторы, вычисленные в двух предыдущих параграфах и интегрируя можно записать общее преобразование в равноускоренную систему отсчёта в виде shWt — U1chWt / /   1 、 U3

√1 - u2      1 W    √1 - u2

r³ + w vr—u²

(7.2)

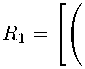
1+ 1u-2√11--uu22 u21  chWt

u1

1-u

2 shWt

1    1 - √1 - u2

L¹ + W 丿+ 〃 2 " 1 — u 2 9^{3 r}3 ^—

W

₁₊ 1_u-_2√11_--_uu₂2 _u2₁

,

(7.3)

R2 = r2 ,

(7 ・ 4)

R3

u3

1 - u2

1 - 1 - u2

u2

u1 ch Wt - shWt

( ^r1+ 京) + (1+

1 - √1 - u2 u2√1 - u2

)r3-

Заключение

В заключение подчеркнём, что известный закон гиперболического движения частицы под действием постоянной силы не имеет отношения к задаче о равноускоренном движении. Равноускоренная система отсчёта двигается таким образом, что её частоты собственной прецессии Томаса (3.8) и собственного вращения Вигнера (3.1) взаимно компенсируются и результирующее вращение равноускоренной системы s равно нулю, как это и должно быть.

Наиболее общее преобразование в равноускоренную систему отсчёта можно найти минимум тремя способами: простым лоренцевским бустом (п. 2), решением уравнений (4.2), (4.3) обратной задачи кинематики (п. 4) и решением уравнений движения тетрады (п. 5). Совпадение параметров равноускоренной системы отсчёта, полученных решением уравнений (4.2), (4.3) или уравнений (5.1), (5.2) с параметрами полученными лоренцевским бустом (2.1)-(2.3), (2.9)-(2.11) позволяет даже осторожному исследователю сделать вывод, что уравнения обратной задачи кинематики и уравнение движения тетрады эквивалентны друг другу, проверены и полностью обоснованы.

Трёхмерный вектор скорости начала системы отсчёта, выраженный в собственной системе координат вместе с матрицей направляющих косинусов и тетрада ортонормированных 4-векторов, конечно же, не исчерпывают всё множество возможных кинематических способов представления движения жёсткой системы отсчёта. Поэтому представляет интерес и задача нахождения уравнений, аналогичных уравнениям обратной задачи кинематики или уравнениям движения тетрады для другой возможной параметризации ориентации пространства-времени, например, с помощью бикватернионов. Эта задача предлагается к решению всем заинтересованным специалистам.

Автор благодарит профессора Н. Г. Мигранова за полезные советы, замечания и поддержку.