Некоторые вопросы локально-равновесной термодинамики и ее приложения к построению определяющих соотношений

In this work of questions of constitutive equations of micro nonuniform mediums with help an axiomatic of the locally - equilibrium thermodynamic theory construction are considered.

The first part is dedicated to presentation of the fundamentals of the locally - equilibrium theory and the basic terms ((non)equilibrium of the thermodynamic systems, (non)reversibility in the thermodynamic systems, entropy etc.). In the second part the principles of constitutive equations of micro nonuniform mediums based on internal latent variables construction and application of these principles at designing of constitutive equations with usage of the locally - equilibrium theory are set up.

В работе рассматриваются вопросы, связанные с построением определяющих соотношений (ОС) микронеоднородных сред с помощью аксиоматики локальноравновесной термодинамической теории (ЛРТ).

Основные принципы ЛРТ была сформулированы Афанасьевой-Эренфест в 30-х годах XX века [1], тем не менее и по сей день существует много вопросов, касающихся правомерности использования данной теории в целом и некоторых ее положений, в частности, при описании термомеханических явлений в материалах.

Общий подход ЛРТ заключается в попытке обобщения основных понятий и принципов термостатики на нестационарные процессы, протекающие в сплошной среде. Несмотря на то, что основные немеханические величины, такие как температура и энтропия, определялись термостатикой только в положении равновесия, удалось построить теорию, описывающую необратимые термомеханические явления в сплошной среде при определенных ограничениях, например, на скорость распространения возмущений в среде, которая должна быть значительно меньше, чем скорость релаксации ^* в элементарном объеме.

Именно в обобщении термостатики, которым пользуется ЛРТ, кроются ее основные преимущества и недостатки. К недостаткам можно отнести спорность основных положений самой термостатики [2], а к преимуществам можно отнести обоснованность таких понятий, как температура и энтропия, замкнутость теории (вместе с соотношениями Онзагера и вариационными принципами ЛРТ), а значит, и возможность ее использования при построении ОС.

В первой части авторы попытались изложить основы ЛРТ и еще раз остановиться на основных вопросах, связанных с применением положений ЛРТ при построении ОС. Вторая часть работы посвящена общим принципам построения ОС микронеоднородных сред на основе ЛРТ и использования внутренних переменных.

Общие вопросы неравновесной термодинамики

1. Основы локально-равновесной термодинамики

Применение равновесной термодинамики при исследовании термодинамических процессов в значительной степени основано на следующей гипотезе: при переходе из одного равновесного состояния термодинамической системы в другое в пространстве термодинамических переменных найдется путь, двигаясь по которому, ТДС будет находиться в состоянии равновесия в любой момент времени. Такой процесс принято называть квазиравновесным или квазистатическим . Считается, что если изменение внешних термомеханических нагрузок происходит достаточно медленно (по сравнению со скоростями релаксационных процессов), то отклонение от положения равновесия всех частей исследуемой ТДС будет незначительным и недолговременным, поэтому им можно пренебречь. Можно ли пренебречь даже незначительным отклонением от положения равновесия, остается вопросом, учитывая, что эти отклонения могут накапливаться в процессе перехода из одной точки в другую, вызывая качественные эффекты, например, необратимость процесса.

Полагается, что любой квазиравновесный процесс обратим. Это прямое следствие из аксиоматики Каратеодори; тем не менее, существует иное мнение. Оно опирается на следующие рассуждения. Какими бы ни были медленными процессы, например, диффузия или теплообмен, они необратимы. Такое несоответствие можно объяснить, если понять, что квазиравновесные процессы во многом являются воображаемыми и имеют мало общего с реальностью. Строго говоря, они даже не являются процессами, так как представляют собой множество равновесных точек, которые можно достичь, устремляя скорости изменения термодинамических величин к нулю. В этом смысле выводы, полученные термодинамикой для квазиравновесных процессов, играют роль предельных теорем [3]. Из этих рассуждений можно сделать следующий вывод. Математическая термодинамическая теория, построенная Каратеодори и его последователями, изучает воображаемый процесс, который является обратимым и состоит из точек равновесных состояний ТДС.

Для более адекватного описания термодинамического процесса нужно учитывать, что они протекают с конечной скоростью и отклонения от положения равновесия бывают значительными (например, тепло- и массоперенос в сплошной среде). Поэтому равновесная термодинамика (термостатика) является весьма грубым приближением и не может удовлетворять исследователей, которые нацелены на построение адекватной теории поведения исследуемого объекта. С другой стороны, необходимо отметить, что в результате своего развития равновесная термодинамика обогатилась собственной аксиоматикой, математическим аппаратом, основными понятиями, такими как температура, энтропия и т.д. В связи с этим возникает желание обобщить принципы и подходы термостатики на неравновесные термодинамические процессы.

В данной работе мы будем рассматривать один из известных подходов обобщения классической термодинамики на неравновесные процессы. Эта теория носит название локально-равновесной термодинамики ^† . В данной теории исходят из представления о локальном равновесии элементарного объема [4,5]. Классическая термодинамика не определяла понятие элементарного объема материала. В работах Кельвина, Карно, Каратеодори речь шла о телах. Здесь уместно провести аналогии с механикой: Бриджмен, Юнг и Гук ставили опыты и затем формулировали законы для

Общие вопросы неравновесной термодинамики образцов (тел), и только с развитием механики деформируемой сплошной среды возникло понятие элементарного (представительного) объема, для которого закон Гука с успехом применяется в обобщенном виде.

В качестве представительного объема будет рассматриваться минимальный объем материала, содержащий достаточное для статистического описания его состояния число «носителей» рассматриваемых механизмов процесса (атомов, молекул, например, в упругих телах, жидкостях, газах; точечных дефектов, дислокаций при анализе ползучести и пластичности твердых тел). Добавление к этому объему других частей рассматриваемого материала с аналогичной (в статистическом смысле) конфигурацией «носителей» анализируемых механизмов не должно приводить к изменению эволюции конфигурации «носителей» при одинаковых однородных воздействиях. Иначе говоря, для построения ОС каждого масштабного уровня необходимо определение некоторого минимального объема материала, реакция, отклик которого будут идентичны реакции большего объема того же материала при тех же воздействиях. При этом параметры, характеризующие как реакцию материала, так и воздействие на него, усредняются по представительному объему, что необходимо учитывать при анализе получаемых результатов решения краевых задач. При рассмотрении полей характеристик материала значения последних в каждый момент времени в каждой геометрической точке определяются как осредненные по «скользящему» пространственно-временному элементу (представительному объему) величины, отнесенные к выбранной по соглашению точке этого элемента (как правило, «центру масс»).

Представительный объем трактуется как открытая термодинамическая система, т.к. через его поверхность возможен и тепло-, и массоперенос.

Вернемся к гипотезе локального равновесия. Хотя данная гипотеза ограничивает область применимости данного подхода, существует мнение [6], что везде, кроме турбулентных явлений, быстрых процессов в плазме и ударных волн, гипотеза локально-равновесного процесса приемлема. Данный вывод опирается на экспериментальные данные, приведенные, например, в работах Пригожина, Мейкснера и Рейка и других авторов [7, 8, 9].

Локально-равновесный процесс нельзя понимать как процесс в полном смысле этого слова; скорее, его следует рассматривать как ряд последовательных равновесных состояний элементарного объема. Каждое из этих состояний определяется конечной совокупностью равновесных термодинамических переменных и их значений [10]. Более того, только для данных состояний и можно ввести понятия температуры и энтропии ^* . При переходе из одного локально-равновесного состояния в другое энтропия элементарного объема изменяется «скачкообразно», что эквивалентно возникновению энтропии в рассматриваемом объеме, которое называют производством .

Можно ли считать, что если в локальных объемах реализуется квазиравновесный процесс, система в целом может являться неравновесной? В механике деформируемого твердого тела (МДТТ) хорошо известен принцип макрообразца: изучение поведения любой локальной (малой) макроскопической области материала (представительного объема материала), являющейся «частицей» деформируемого тела, можно свести к исследованиям на образце макроскопических размеров, при условии, что в нем реализуется однородное термомеханическое состояние. Заметим, что само тело конечных размеров при этом может испытывать неоднородные воздействия, имеющие откликом неоднородные поля напряжений,

Общие вопросы неравновесной термодинамики деформаций, температур и т.д. Воспользуемся аналогичным приемом для попытки сравнения локально-равновесного и квазиравновесного процесса. Для исследования процесса, происходящего в элементарном объеме, рассмотрим макрообразец, который в каждый момент времени находится в термодинамически однородном состоянии равновесия. Будем называть его телом. Температура тела равна 01. В некоторый момент времени тело соприкасается с термостатом, имеющим температуру 0 2 >01. Между термостатом и телом начнется процесс теплообмена (нагревание тела). В результате этого за время dt термостат потеряет, а тело приобретет количество тепла 5H . Предположим, что скорость теплообмена постоянна и равна h , т.е. 5H = hdt. Подсчитаем, насколько изменится энтропия системы тело - термостат. Как известно, энтропия - аддитивная величина, поэтому изменение энтропии всей системы в целом равно сумме изменений энтропии термостата и тела, dS (t ) = dS, (t)+ dS, (t )=--H + 5H ■ = h (—U--^ I dt > 0.

^2VI               0 2 ( t )     0 , ( t )     (0 , ( t ) 0 2 ( t ) J

За промежуток времени At изменение энтропии составит t о+A if ,           , A

A S = h \ Ц dt .

, ( (0 , ( t ) 0 2 ( t ) J

Термостат, по определению, также является телом (значительно больших массы и объема по сравнению с рассматриваемым телом). Следовательно, здесь идет речь о теплообмене между двумя телами, в результате которого возникает положительное приращение энтропии. При этом нужно учесть, что в рассматриваемых телах совершается квазиравновесный процесс, для которого справедливо соотношение Клаузиуса - Планка dS = 5 H /0 . Система термостат - тело в целом ведет себя как неравновесная система [11]. Возвращаясь к сплошной среде, можно сделать вывод, что система, состоящая из элементарных объемов (окружающая его сплошная среда принимается в качестве термостата), в каждом из которых возможен только квазиравновесный процесс, в целом ведет себя как неравновесная система.

Из последнего соотношения можно сделать еще один важный вывод. Если устремить скорость теплообмена к нулю, то из ограниченности интеграла следует, что A S ^ 0. Приходим к "классическому" квазиравновесному процессу. Таким образом, h ^ 0

локально-равновесный процесс отличается от квазиравновесного тем, что проходит с конечной скоростью и в результате приводит к производству энтропии.

Поскольку элементарный объем в ЛРТ представляет собой классическую квазиравновесную ТДС, необходимо выбрать термодинамический потенциал , описывающий равновесные состояния элементарного объема, а также независимые характеристические термодинамические величины , относительно которых выбранный потенциал будет иметь экстремум в состоянии равновесия. В качестве такого потенциала может быть использована локальная энтропия s ( r , t ) , которая представляет собой полевую скалярную величину, зависящую от соответствующих характеристических термодинамических величин, которыми, как известно, являются внутренняя энергия u ( r , t ) и обобщенные характеристические координаты a i ( r , t ), относительно которых элементарное приращение энтропии есть полный дифференциал. Выбор характеристических переменных зависит от того, модели каких

Общие вопросы неравновесной термодинамики сред строятся. Например, если рассматривать квазиравновесные процессы в газах, для энтропии характеристическими являются внутренняя энергия и объем, для многокомпонентных гидродинамических сред – внутренняя энергия, объем и концентрация компонент.

Таким образом, будем полагать, что состояние элементарного объема в окрестности точки r в момент времени t описывается локальной энтропией

5 = 5 ( u ( r , t ), a ( r , t ) ) ,                                                          (1.1)

определяемой из обобщенного уравнения Гиббса для квазиравновесных процессов du = 0ds + У J idai,                                            (1.2)

где Ji – обобщенная сила, сопряженная с обратимым элементарным изменением обобщенной характеристической координаты ai . Для того чтобы пояснить, что понимается под «сопряженностью» обобщенной силы, необходимо вернуться к вопросу об обратимости ТДС в квазиравновесном процессе.

Приведем одну из возможных математических формулировок обратимости. Для произвольного циклического квазиравновесного процесса справедливо

A u = f ( 0 ds + ^ J i da i ) = 0,

(1.3)

(1.4)

или в более привычном виде

A s = f — du - У — da: 1 = 0.

J^0    ^0   ¹ )

В силу независимости внутренней энергии и характеристических координат (т.к. характеристические термодинамические величины считаются независимыми), а также в силу произвольности процесса, необходимо потребовать, чтобы для любых i выполнялось условие:

f l

0 du 1 = 0, f⁽ J i da i ) = 0, ^.

(1.5)

Будем полагать, что d го i = Jda^, где d го i - обратимое элементарное изменение удельной энергии. Таким образом, в рассматриваемом процессе необходимо выделить те механизмы, которые приводят к обратимым изменениям удельной энергии, и так подобрать обобщенные координаты и силы, чтобы для любого i можно было бы всегда записать J i = d гоij da i . В качестве примера рассмотрим модель упругопластической среды. В процессе деформации можно выделить две независимые характеристические обобщенные координаты – упругую и пластическую деформации. Из них только упругая деформация должна войти в последний член соотношения (1.2), так как ее изменение, умноженное на напряжения, дают нам обратимое изменение механической энергии.

Для внесения ясности в рассматриваемый вопрос необходимо вспомнить, что аксиоматика квазиравновесных процессов предполагает наличие таких сил, которые зависят только от равновесного состояния системы, т.е. имеют потенциальный характер относительно деформационных координат ^* [12]. Только при ограничениях подобного рода Каратеодори удалось доказать наличие интегрирующего множителя (температуры) для пфаффовой формы количества тепла. Выражаясь современным языком МСС, можно сказать, что в квазиравновесном процессе работа внешних сил является функцией мгновенного состояния процесса, что накладывает ограничения на учитываемые механизмы деформации. Забегая вперед, уточним, что переход из одного

Общие вопросы неравновесной термодинамики равновесного состояния в другое может сопровождаться изменением пластической деформации, которое учитывается в производстве энтропии, т.е. той части энтропии, которая связана с необратимостью процесса.

Дальнейшие рассуждения строятся на том, что для полевых величин s , u и a_i можно записать уравнения локального баланса:

ds

P =-divI 5 +Х 5 ,1.6)

dt р du = -divIи +Xи ,(1.7)

dt da

P ~ = -divIat +Xa, , dt i i где буквой I обозначается плотность потока соответствующей величины через поверхность элементарного объема, буквой х - производство соответствующей величины внутри элементарного объема. Соотношение (1.8) записано для скалярных характеристических координат. Запишем уравнение (1.2) в скоростной форме, р d! =pf du-у j^ ).                            (1.9)

dt 0< dt ¹ dt J

Подставив (1.7) и (1.8) в правую часть уравнения (1.9), можно получить выражение для производства энтропии х5.

Конкретный вид соотношения для х ₅ является ключевым для ЛРТ и не может быть полностью получен без выяснения класса сред, для которых строится модель. Тем не менее существует возможность уточнить (1.9), не привлекая специфических знаний о моделируемой среде.

В монографии [6] можно найти исчерпывающее доказательство того, что плотность потока внутренней энергии I _u полностью совпадает с тепловым потоком, поэтому, воспользовавшись законом теплопроводности Фурье, можно записать

Iu = Iq =-nV0 , (1.10) где п — коэффициент теплопроводности в моделируемой среде. При этом необходимо учесть, что локальная скорость возникновения внутренней энергии хи по закону сохранения полной энергии равна плотности источника механической энергии с обратным знаком. Этот факт легко доказать, если записать балансовое уравнение для полной E и механической Em энергий, dE

= 0,

р —+ divl e dt р Em^L + divI dt Em

= х E . m

Источник полной энергии E отсутствует в силу закона сохранения энергии. Второе уравнение говорит о том, что элементарный объем не является консервативной системой. Вычтем второе уравнение из первого, а также учтем, что полная энергия является суммой внутренней и механической энергий, u = E - Em , тогда хи =-хe =^ :е,                                               (1.11)

m где о - тензор напряжений Коши, е - тензор полных деформаций. Величина - ст : dе представляет собой работу ТДС, сообщаемую окружающей среде через границу

Общие вопросы неравновесной термодинамики элементарного объема за время dt . Таким образом, балансовое уравнение для внутренней энергии выглядит следующим образом:

р — = - divI., + с : £ .                                            (1.12)

dt ^q

Полученное соотношение хорошо известно в МСС, например, его можно встретить в монографии [13].

С целью дальнейшего уточнения соотношения (1.9) выделим среди всех характеристических переменных те, которые отвечают за обратимое механическое поведение среды. Это означает, что необходимо предположить существование меры деформированного состояния εe , приращение которой в свертке с тензором напряжений с дает элементарное обратимое изменение механической энергии, d ш e = р Jedae =с : d£ e.                                          (1.13)

Подставим (1.12) и (1.13) в (1.9), в результате чего получим

ds р р= dt 0

1 л               т da *

^- ""div ¹ q ^- £ ^Ji

V Р                  dt У

+ —с

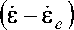
(1.14)

В соответствии с гипотезой аддитивности скоростей деформации разность в последнем члене промежуточного соотношения (1.14) будет представлять собой ту часть деформации объема, которую можно считать необратимой. Например, в качестве таковой может выступать пластическая деформация в моделях упруго-пластических сред. В дальнейшем будем применять обозначение £ p = £ - £ e .

Подставим выражение для баланса характеристических параметров (1.8) в последнее соотношение, после чего получим ds 1                              1             1

Р— =-- ( divL, - / J ,div I„ ) +—с : e„-- 7 J x .

dt 0^V q '     ^aJ 0 p 0^ i

Данное соотношение необходимо преобразовать к виду уравнения баланса (1.6). Для этого применим преобразования, в соответствии с которыми

I

—divL = div — +   L ■ V0 ,

0 q 0  0 ² q

^Ji div I

= div J i I ^- - I_a ■VJ¹- . 0 ^a *     0

В результате получаем окончательный вид балансового уравнения для энтропии локально-равновесной системы

Р ds = - div q ^Л + 1 - -q ■V0-0Y I_arv| JI l + с : £_p-Y J,x_Qi . (1.15) ^pdt V 0 J 0( 0             ^ai (ej p i ^ai J

Последний член соотношения (1.15) определяет производство энтропии в элементарном объеме, т.е.

X s = 0 (- I q ■ ^V0 - ⁰ ^ I ai ■ ^V ( ^0)"^{J + C} : ^£ P - ^ J X a* J .        ⁽¹*¹⁶⁾

Умножая производство энтропии на температуру, можно получить так называемое рассеяние энергии или, по определению Клаузиуса, нескомпенсированное тепло. Это та часть энергии, которая «рассеивается» в элементарном объеме материала за единицу времени в процессе тепло- и массообмена в совокупности с необратимой деформацией.

Введем некоторые обозначения

X q =-ve/e 2 , X i =-V ( j , /0 ) , x _e = £ _p /0 , x i, =- j , /0 .

Общие вопросы неравновесной термодинамики

Данные величины называются термодинамическими силами, каждая из которых сопряжена со своим термодинамическим потоком. Необходимо отметить, что первые три силы сопряжены с векторными и тензорными потоками через поверхность элементарного объема: тепловым потоком, потоком обобщенной координаты a _i и потоком импульса соответственно. И только последняя сила сопряжена с производством обобщенной координаты a _i внутри объема.

Используя введенные обозначения, можно представить производство энтропии в билинейной форме

X s = I a "  Xq + 521 a " X/ + ^ : Xr + 52 Xa Xv -                    (1-17)

• 5 q q           a i i             ь                  X

В литературе чаще всего можно встретить следующую форму записи

• X , = Z I i X i ,                                                   (1-18)

где I_i – независимые скалярные потоки, а X_i – сопряженные с ними скалярные термодинамические силы. При необходимости соотношение (1.17) можно представить в таком же виде. Для этого необходимо отказаться от тензорной формы записи и в качестве термодинамических сил и потоков использовать компоненты тензоров и векторов, входящих в (1.17). Форма записи производства энтропии в виде (1.18) имеет существенное значение для ЛРТ, так как для нее формулируются квазилинейные законы Онсагера (Onsager), связывающие термодинамические потоки и силы.

Будем полагать, что для локально-равновесных процессов справедлива теорема Онсагера [14], которая гласит, что при малых отклонениях от положения равновесия сохраняется линейная связь между потоками и термодинамическими силами, т.е.

N

I i = E L k ^X k                                           (1.19)

k = 1

или

N

X i = Z RJ k ,                                       (1.20)

k = 1

где     Lik – кинетические коэффициенты, которые определяют влияние термодинамических сил на потоки, Rik – коэффициенты сопротивления, определяющие обратное влияние и связанные с кинетическими коэффициентами соотношением ^ RikLkj =^y - В общем случае кинетические коэффициенты могут зависеть от обобщенных характеристических координат a i и температуры, но не от их потоков, поэтому соотношения Онсагера можно считать квазилинейными. Данные соотношения в механике принято называть определяющими соотношениями.

С точки зрения теории определяющих соотношений механики законы Онсагера диктуют вид определяющих соотношений. Кажется странным, что необратимое деформирование любого материала должно описываться квазилинейными связями между напряжениями и скоростью деформации (различными видами теории течения). Чтобы не делать из ЛРТ ^* «теорию мироустройства», хотелось бы еще раз напомнить, что она имеет свои границы применимости. Она описывает поведение ТДС вблизи равновесия и вряд ли ее можно применить для построения модели систем с диссипативными структурами различной природы; систем, находящихся вблизи точек бифуркаций; систем, в которых тепловые и другие потоки достигают существенных

Общие вопросы неравновесной термодинамики величин и к тому же быстро меняются во времени. Для всех систем подобного рода характерное время установления равновесия в локальном объеме значительно больше времени изменения граничных условий на его поверхности и характеристик процессов, происходящих внутри объема. Для таких систем нельзя записать соотношение (1.2), оно превращается в неравенство Клаузиуса – Дюгема, в результате чего вся стройная аксиоматика ЛРТ «рассыпается». Таким образом, результаты, получаемые с помощью ЛРТ, можно считать квазилинейным приближением.

Что же может дать исследователям ЛРТ, кроме тривиальных утверждений ^* ? Оказывается, что не так мало, если задаться целью установить связи между механическими и иными явлениями, например, явлениями электромагнитной природы или кинетикой фазовых переходов. С этой точки зрения нас должны интересовать те кинетические коэффициенты, которые отвечают за перекрестные процессы, т.е. L_ik при i ≠ k .

Рассмотрим свойства матрицы кинетических коэффициентов. Во-первых, в соответствии с принципом микроскопической обратимости ^† Онсагера и дополнениями Казимира можно записать соотношения взаимности Онсагера – Казимира,

L ik = ε i ε k L ki , (1.21)

где ε _i = 1 для скалярных потоков, которые c точки зрения статистической механики зависят от четных функций по времени, и ε _i = - 1 для «нечетных» скалярных потоков [3]. Во-вторых, матрица кинетических коэффициентов должна быть положительно определенной. Это следует из того, что производство энтропии, квадратичная форма записи которого имеет вид

χs =∑LikXkXi , (1.22) i должно быть больше или равно нулю. И, наконец, для уточнения матрицы кинетических коэффициентов применяется принцип Кюри о сохранении симметрии причины в симметрии следствий. Система линейных соотношений (1.19) или (1.20), в зависимости от симметрии среды, должна быть инвариантна относительно соответствующих ортогональных преобразований. При преобразованиях потоки и силы ведут себя по-разному (в зависимости от своей тензорной размерности), в то время как установленная связь между ними не может изменяться при преобразованиях такого рода. Таким образом, при рассмотрении изотропной среды это приводит к сохранению связей Lik лишь между потоками и силами одной тензорной размерности.

Данное утверждение не является бесспорным. Дело в том, что для тензорных величин могут использоваться инварианты, которые, в принципе, могут войти в соотношения для скалярных сил или потоков. Здесь хотелось бы отметить, что законы Онсагера не могут рассматриваться в отрыве от ЛРТ, и поэтому, если в соотношении (1.17) инварианты тензорных величин удастся обнаружить, они окажут влияние на скалярные потоки.

В дальнейшем мы ограничимся рассмотрением изотропных сред, хотя существуют работы (например, [6]), где рассматриваются анизотропные среды и соответствующая модификация принципа Кюри.

Общие вопросы неравновесной термодинамики

Обратимся к тензорной форме записи производства энтропии (1.17), предварительно выделив производство энтропии за счет формоизменения в отдельное слагаемое. В результате получим

χ s = I q ⋅ X q + ∑ I a_i ⋅ X i + S:X ′ ε + pV ^& + ∑ χ a_i X ⁱ χ ,              (1.23)

где S , X ′_ε – девиаторы тензора напряжений и скорости неупругих деформации соответственно, p , V – давление и скорость изменения объема. В этом соотношении можно выделить следующие группы слагаемых одинаковой тензорной размерности: тепловой поток и потоки обобщенной координаты a_i через поверхность объема (векторы); девиатор напряжений как поток импульса (тензор 2-го ранга со следом, равным нулю); скалярные потоки, равные производству a_i внутри объема, и давление. В соответствии с принципом Кюри можно утверждать, что для изотропной среды компоненты векторных потоков не будут влиять на скалярные силы или компоненты тензорных сил, так же, как компоненты девиатора напряжений не будут зависеть от скалярных сил. Предположим, что рассматривается вязкая многокомпонентная гидродинамическая среда с химическими реакциями. Если данная среда изотропна, то на скорость химической реакции может повлиять только давление, но не тепловой поток или, скажем, сдвиговые напряжения. Таким образом, из требования χ _s ≥ 0, принципа Кюри и независимости термодинамических потоков следует, что для изотропных сред можно записать

χ ⁽ s ⁰⁾ = pV ^& + ∑ χ ai X χ ⁱ ≥ 0,

χ ⁽ s ¹⁾ = I q ⋅ X q + ∑ I ai ⋅ X ai ≥ 0,                                      (1.24)

χ ⁽ s ²⁾ = S ⋅ X ′ ε +≥ 0.

Первое неравенство в (1.24) определяет взаимодействие источников обобщенных скалярных координат a_i внутри объема и механического давления. Второе неравенство определяет производство энтропии за счет теплопереноса и, возможно, связанными с ним процессами переноса обобщенных скалярных координат a _i . Например, в качестве таковой может выступать концентрация компонент в многокомпонентной среде. Эффект влияния теплового потока на перенос вещества известен как процесс термодиффузии (эффект Соре), а обратное влияние известно как эффект Дюфора. Третье неравенство утверждает, что работа на неупругих деформациях положительна (для упруго-пластической среды данное неравенство известно под названием постулата Друккера). Попутно из него следует, что на скорость деформации могут повлиять только напряжения. Если это не так, и на скорость деформации или на напряжения влияют другие потоки или силы, то возможно одно из двух: или среда анизотропная, или в системе существует обобщенная координата немеханической природы, которую можно записать в виде тензора 2-го ранга со следом, равным нулю.

Общие вопросы неравновесной термодинамики

Процессы неупругого деформирования и эволюция структуры тесно взаимосвязаны: с одной стороны, макронагружения (макродеформации) являются источником, движущей силой изменения мезо- и микроструктуры; с другой стороны, эволюция мезо- и микроструктуры является определяющим фактором поведения материала на макроуровне. В связи с этим появляются, по крайней мере, две возможности учета эволюции мезо- и микроструктуры: неявным или явным способом. В первом случае в структуру ОС вводятся достаточно сложные операторы над историей макронагружения (макродеформации), без использования соответствующих параметров, описывающих собственную эволюцию мезо- и микроструктуры. Как правило, в этом случае трудно выявить и обосновать физический смысл, механизмы деформирования, описываемые различными операторами модели материала.

В последние десятилетия все большее признание находит второй подход – явное введение в структуру определяющих соотношений конечного множества параметров, описывающих состояние и эволюцию мезо- и микроструктуры, формулировка эволюционных (кинетических) уравнений для этих параметров, называемых внутренними переменными . В литературе, посвященной различным теориям процессов необратимого деформирования, внутренними переменными называют параметры, отражающие структуру и механизмы деформирования на мезо- и микроуровнях. К основным преимуществам этого подхода относятся ясность физической интерпретации эволюционных и определяющих соотношений, возможность прямой или косвенной проверки результатов анализа эволюции мезо- и микроструктуры, относительная простота совокупности уравнений модели (определяющих и эволюционных), широкие возможности обработки результатов решения эволюционных уравнений при переходе к макропеременным (с использованием различных операторов осреднения). Кроме того, поскольку эволюционные уравнения описывают фундаментальные физические механизмы, реализуемые в широком классе реальных материалов, модели данного типа обладают значительной универсальностью. К основным недостаткам рассматриваемого подхода следует отнести: большое число внутренних переменных и соответствующих эволюционных уравнений, необходимых для адекватного описания процесса необратимого деформирования; трудности решения «проблемы замыкания» (установление соотношений между внутренними переменными и макропараметрами); отсутствие в подавляющем большинстве случаев аналитических решений системы эволюционных и определяющих соотношений, что приводит к необходимости использования численных методов.

Следует отметить, что с учетом приведенного выше определения внутренних переменных, в настоящее время невозможно назвать какую-либо теорию необратимых деформаций, не использующую явно или неявно эти переменные. Например, в классической теории пластичности широко применяется понятие поверхности текучести, отделяющее в пространстве напряжений (или деформаций) области упругого и неупругого деформирования. В процессе деформирования поверхность текучести изменяет свою форму и размеры, перемещается как целое. Эта эволюция поверхности текучести отражает изменение свойств материала, обусловленное изменением мезо- и микроструктуры, в связи с чем параметры, описывающие эволюцию этой поверхности, с полным правом можно отнести к внутренним переменным. Аналогичная ситуация имеет место и в других теориях (вязкоупругости, вязкопластичности, ползучести и др.).

В связи с вышесказанным в структуре ОС, описывающих процессы необратимого деформирования, должны фигурировать внутренние переменные . В качестве последних будут использоваться тензорзначные переменные J р , р = 1, B (произвольной в общем случае валентности); вопрос о типе, физическом смысле и

Общие вопросы неравновесной термодинамики аргументах внутренних переменных решается в рамках конкретных теорий ОС. В частности, в качестве внутренних переменных могут фигурировать тензоры второго ранга, определяющие ориентацию кристаллографической системы координат зерен поликристалла относительно лабораторной системы отсчета; потребность во введении подобного рода переменных возникает при необходимости описания возникновения и эволюции текстуры при глубоких пластических деформациях.

Следует отметить, что часть внутренних переменных непосредственно входит в структуру ОС данног о ма сштабного уровня, такие переменные в дальнейшем будем обозначать J | , в = 1, B и для ясности называть их внутренними «явными» переменными. К числу таких переменных относятся, например, параметры, характеризующие форму, положение и размеры поверхности текучести в теориях пластического течения.

Вторая группа внутренних переменных (в большинстве случаев относящихся к более глубоким масштабным уровням) входит в качестве переменных в э вол юционные уравнения (ЭУ); переменные этой группы будем обозначать как J р , в = 1, B ; для того чтобы отличать их от переменных первой группы, будем называть их внутренними «скрытыми» переменными. К числу таких переменных в теориях неупругого деформирования поликристаллов (мезо- и макроуровней) можно отнести, например, плотность краевых и винтовых дислокаций. Полная совокупность внутренних переменных, таким образом, определяется как

{ j p } = { j e , J 5 } , в = VB , Y = 1, B^e , 5 = 1, B ' , B = B e + B ' .

Введем в рассмотрение симметричный тензор второго ранга J ¹ со следом, равным нулю, , который является мерой структурных изменений, происходящих в материале. С точки зрения ЛРТ производная от данной внутренней переменной J ^ir будет термодинамическим потоком. Пусть для рассматриваемой внутренней переменной был подобран сопряженный тензор X ⁱ , который является интенсивной термодинамической величиной и в нашей терминологии называется термодинамической силой. Двойная свертка введенного потока и силы войдет в выражение для производства энтропии, а точнее, в третье неравенство (1.24).

Мы намеренно опустили вопросы нахождения внутренних переменных и формулирования для них эволюционных и замыкающих уравнений, которые являются важнейшими этапами при построении физически обоснованных ОС материала. Это было сделано для того, чтобы сосредоточиться на основной в данный момент задаче, которую можно сформулировать следующим образом: конструктивное использование ЛРТ при построении ОС.

При получении конкретного вида ОС в ЛРТ можно воспользоваться вариационными принципами термодинамики. Одним из первых вариационных принципов был принцип наименьшего рассеяния энергии Онсагера (Onsager), который получил свое развитие в работах Махлупа (Machlup), Тиссы (Tisza) и Маннинга (Manning), Дьярмати (Gyarmati). Тем не менее наибольшую известность снискал себе широко используемым принцип минимального производства энтропии Пригожина (Prigogine), который, не являясь независимым принципом ^* , все же удобен в применении к изучению стационарных явлений[6, 15].

В рассматриваемой задаче будем использовать принцип наименьшего рассеяния энергии. Сам принцип базируется на двух потенциальных функциях

Общие вопросы неравновесной термодинамики

• * ( X, X ) = ¹ Z L ik X i X k ,

2                                                         (2.1)

ф( I, I)=2 Z RM, которые называются локальными потенциалами рассеяния. Потенциалы *(X, X), Ф(I, I) являются локальной мерой неравновесности и отличаются друг от друга лишь способом описания неравновесного состояния. Действительно, *(X, X) зависит только от сил, которые определяют само неравновесное состояние, а Ф(I, I) является функцией потоков и характеризует неравновесное состояние в зависимости от параметров состояния. Доказательство того, что функции имеют потенциальный характер, можно найти в работе [6]. Первые производные от потенциалов содержат линейные соотношения Онсагера, а легко доказываемое равенство вторых смешанных производных эквивалентно соотношениям взаимности.

Локальная форма принципа наименьшего рассеяния энергии может быть представлена через потоки

8 [ х s - Ф ] x = Z ( X k --Ц ф] ⁸ I k = 0

(2.2)

(2.3)

или через силы

8 [ Х , — * ] I = z f I k - * 8 X_k = 0.

V     ^{d X}k J

С практической точки зрения представление в термодинамических силах удобнее, чем представление через потоки, хотя с математической точки зрения они эквивалентны. Необходимо отметить, что достаточным условием существования экстремума (2.2) или (2.3) является наличие линейных соотношений Онсагера и соотношений взаимности.

Воспользуемся (2.3) для вывода ОС микронеоднородной среды. Согласно (2.3) в силу независимости потоков получим три уравнения: для скалярных, векторных и тензорных сил и потоков. Первые два уравнения дают нам известные линейные законы связи объемной деформации и давления, а также закон Фурье. Это понятно, так как мы не предполагали наличие скалярных либо векторных внутренних переменных. Третье уравнение можно разбить на два, опять же в силу независимости потоков,

X ' - R sj J^ir - R s S = 0, X i - R sj S - R j J ^ir = 0.

(2.4)

Из последних соотношений немедленно следуют тензорно-линейные несоосные ОС в виде

X ' = A S + B X i , (2.5) где A = R s - R sj² R j , B = RR .

Физический смысл соотношений (2.5) состоит в том, что скорость неупругой деформации определяется не только потоком импульса, носителем которого является девиатор напряжений, но и некой интенсивной термодинамической величиной, связанной с эволюцией микроструктуры материала и имеющей тензорную природу.

В качестве примера можно привести твердотельные фазовые переходы и их влияние на деформацию формоизменения. В работе [16] вводится понятие тензора концентрации и сопряженного с ним тензора химического потенциала. Обоснование необходимости введения такого рода величин при моделировании твердотельных фазовых переходов также можно найти в работах [17, 18, 19]. Будем считать, что X ⁱ в

Общие вопросы неравновесной термодинамики соотношении (2.5) есть тензор химического потенциала  St = Xi. Введем непринципиальное упрощение: будем считать, что след этого тензора равен нулю. В данном случае уравнение (2.5) указывает на связь процессов изменения фазового состава и пластичность превращения, т.е. неупругую деформацию формоизменения, связанную с происходящими в твердом теле процессами структурного фазового перехода одного типа кристаллической решетки в другой.

Роль эволюционных уравнений выполняют уравнения Онсагера, которые связывают внутренние «скрытые» переменные, такие как Jt = Jir - тензор скорости роста новой фазы, – с термодинамическими силами, такими как St – тензор химического потенциала. Для дальнейшего анализа нам потребуется замыкающие уравнение для S t или сопряженного с ним тензора Jt . Будем полагать, что существует такая тензорзначная функция F(S) , при которой

S t = F ( S ).

(2.6)

Данное уравнение определяет, что химический потенциал зависит от напряжений, и требует пояснения. Известным [20] является тот факт, что напряжения влияют на способность к развитию зародышей новой фазы, а также на интенсивность химических реакций. Это объясняется тем, что энергия межфазной границы зависит от напряжений в фазах, а значит, и условие химического равновесия фаз находится под их влиянием. В (2.6) мы пренебрегаем другими эффектами, влияющими на условие химического равновесия межфазной границы, такими как тип и «шероховатость» межфазной границы или концентрационное переохлаждение (для многокомпонентных сред) [21, 22].

Построим линейное приближение (2.6). С этой целью разложим (2.6) в ряд Тейлора и ограничимся первым членом разложения. В результате получим аг

(2.7)

S, = : S= H : S, t где H – тензор четвертого ранга, определяющий коэффициенты чувствительности химического потенциала к напряжениям. В общем случае тензор H может зависеть и от строения трансформирующегося материала, направления кристаллографических осей обеих фаз на межфазной границе и т.д.

Подставив (2.7) в (2.5), получим

X ; = ( A C_n + B H ) : S . (2.8)

Полученные уравнения (2.8) представляет собой структуру ОС с внутренними связями для материалов, проявляющих эффект пластичности превращения. Неизвестные кинетические коэффициенты, а также компоненты тензора чувствительности H могут быть определены из экспериментов.

В данной работе авторами были рассмотрены вопросы, связанные с применением локально-равновесной термодинамики к построению ОС. Хотя сегодня существует множество других аксиоматических теорий, таких как рациональная термодинамика [2], расширенная термодинамика [23], локально-равновесная теория по-прежнему популярна среди исследователей. Причиной популярности, каким бы странным это ни показалось, может являться спорность некоторых положений данной теории. Именно они заставляют задуматься над природой тепла (особенно в твердом теле) и искать ответы на, казалось бы, очевидные вопросы, такие как: что представляют собой температура и энтропия, чем вызвана диссипация механической энергии в материале и т.д.

Общие вопросы неравновесной термодинамики

Эти вопросы становятся критичными, когда исследователи начинают изучать микронеоднородные среды на разных масштабных уровнях. Они трансформируются в актуальные и по сей день трудноразрешимые проблемы, связанные с синергетикой поведения разномасштабных дефектов структуры.

Найти подходы к решению подобных проблем, используя только термодинамику, не представляется возможным, хотя существуют такие попытки [24, 25]. Классификация внутренних переменных и уравнений, входящих в структуру ОС, является важным этапом построения физически обоснованных ОС. Авторы планируют развитие данной методики и ее совместное применение с другими термодинамическими теориями.

Работа выполнена при финансовой поддержке РФФИ (грант №04-01-00549).