Некоторые вопросы проектирования аксиально-плунжерных гидромашин с наклонной шайбой, форсированных по давлению

Тенденция непрерывного увеличения рабочего давления объемных гидромашин, являющихся основными компонентами гидравлического привода, привела к появлению новых условий и новых требований, предъявляемых к их конструкции.

Рассмотрим эти особенности на примере аксиально-плунжерных гидромашин с наклонной шайбой с самоустанавливающимся блоком цилиндров с опорой на валу [1]. Рабочее давление таких гидромашин в настоящее время достигло значений р 2 = 40 + 45 МПа. Увеличение рабочего давления на нагнетании объемных гидромашин вызывает значительное возрастание двух факторов:

– увеличивается суммарное усилие, действующее на плунжеры, находящиеся на стороне на- гнетания, в том числе возрастает его статическая составляющая;

– значительно увеличивается динамическая составляющая указанного усилия за счет интенсификации динамических процессов на стороне нагнетания.

Указанные факторы приводят к увеличению тангенциальных составляющих

F г к = F p к tg / ш                                      (1)

и их равнодействующей, передающейся со стороны блока цилиндров на вал z2

F T к S = 2 F T к ,                                    (2)

к = 1

где

F Р к = Р 2 ( t ) ^

– усилие, действующее на k -й плунжер;

d _п – диаметр плунжера;

p ₂ ( t ) - давление в полости цилиндра;

У _ш — угол наклона шайбы;

z ₂ – число цилиндров, находящихся в зоне нагнетания.

Так как равнодействующая F _г к _S содержит как статические, так и динамические составляющие усилий, действующих на плунжеры, то в общем случае она может быть представлена как сумма статических и динамических составляющих, т.е.

F T к S = F T к S c + F T к S ( t ) ,                                     (3)

где F _{г к S c} - статическая составляющая усилия;

F г _{к S} ( t ) — динамическая составляющая усилия.

Первая (статическая) составляющая вызывает нагружение вала гидромашины и его подшипников – опор, а вторая (динамическая) составляющая – вынужденные колебания вала и ротора гидромашины и дополнительные нагрузки на подшипники. Под действием статической состав- ляющей поперечного усилия происходит прогиб вала, вызывающий перемещение передней части блока цилиндров, для которого вал является опорой. В результате перемещения блока цилиндров возможно раскрытие зазора между блоком и торцевым распределительным золотником и как следствие потеря работоспособности гидромашины. В таких условиях для оценки работоспособности гидромашины важнейшую роль приобретает определение деформации вала, а не напряжений, возникающих в его сечениях (как это принято в других отраслях машиностроения).

Вообще говоря, это положение справедливо для всех видов объемных гидромашин, имеющих кинематические пары аналогичного типа: пластинчатых, шестеренных и т.д.

Анализ конструкций аксиально-плунжерных гидромашин с наклонной шайбой отечественного и зарубежного производства позволяет выделить три схемы роторов, которые характеризуются применением различных типов подшипников. Наличие в качестве опор шариковых радиально-упорных подшипников, роликовых подшипников с короткими роликами (с учетом радиальных зазоров) и конических роликовых подшипников короткими роликами (с учетом радиальных зазоров), образующих кинематические пары 3 класса, (рис. 1а) дает возможность представить расчетную схему ротора в виде вращающейся балки на двух шарнирных опорах, показанных на рис. 1б. Обозначим эту схему цифрой I.

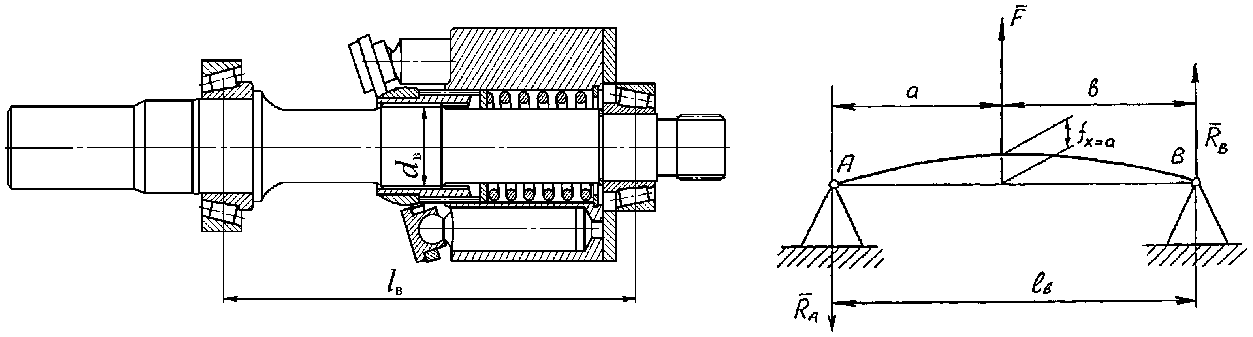
а)                                                                         б)

Рис. 1. Ротор аксиально-плунжерной гидромашины:

а – ротор аксиально-плунжерного насоса фирмы Sauer-Danfoss; б – расчетная схема I вала

Для второго основного вида роторов характерно применение в качестве опор роликовых подшипников с длинными роликами, игольчатых подшипников или удлиненных подшипников скольжения, образующих кинематические пары 4 класса (рис. 2а), что позволяет представить расчетную схему ротора в виде вращающейся балки на двух опорах в виде заделки, показанную на рис. 2б. Обозначим эту схему цифрой III.

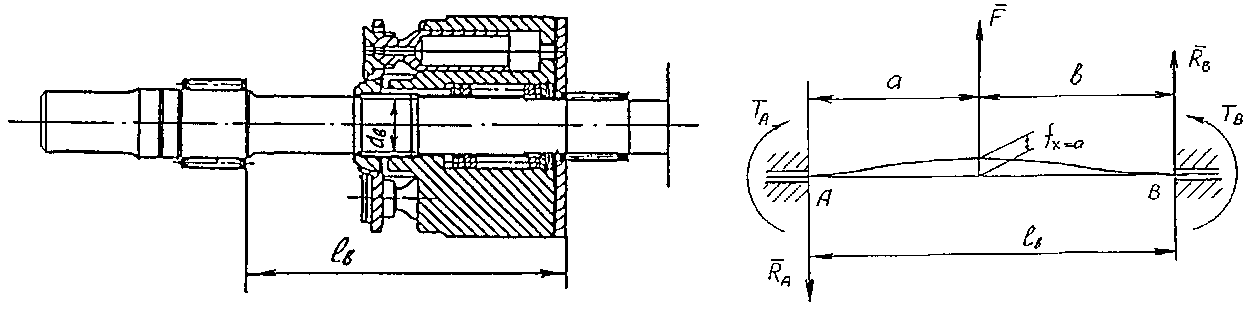
Рис. 2. Ротор аксиально-плунжерной гидромашины:

а – ротор аксиально-плунжерного насоса фирмы EATON; б – расчетная схема III вала

К промежуточным можно отнести вид роторов, в которых в качестве передней опоры применяется радиально-упорный шариковый подшипник или роликовый подшипник с короткими роликами, а в качестве задней опоры – роликовый подшипник с длинными роликами, игольчатый подшипник или удлиненный подшипник скольжения (рис. 3а). Расчетную схему можно представить в виде вращающейся балки на двух опорах: передняя является шарнирной, а задняя – заделкой (рис. 3б). Обозначим эту схему цифрой II.

Расчет и конструирование

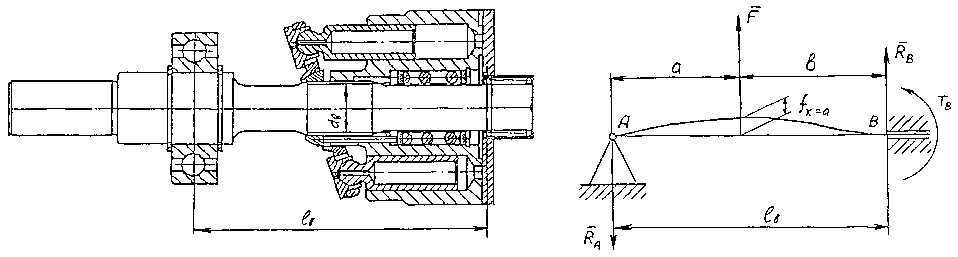
б)

а)

Рис. 3. Ротор аксиально-плунжерной гидромашины: а – ротор аксиально-плунжерного насоса фирмы Bosch-Rexroth; б – расчетная схема II вала

Сравним расчетные значения прогиба вращающихся валов под действием поперечного усилия F, выполненных в соответствии с расчетными схемами I, II, III при условии равенства их геометрических размеров: dв, lв, a, b и при a = b = 2^

.

Прогиб балки в сечении x = a для всех трех схем определяется соотношением

fx = a = -в- C i , CM ,

JE где F – поперечное усилие, кг;

l _в – расчетная длина вала (расстояние между опорами), см;

Е – модуль упругости материала, кг/см²;

П

J = 64 d _в - момент инерции сечения вала, см ;

d _в – диаметр вала, см;

C i – расчетный коэффициент.

Значения расчетного коэффициента представлены в табл. 1.

Таблица 1

Схема вала	C i	C i / С I
I	0,02	–
II	0,009	0,45
III	0,005	0,25

Из данных табл. 1 следует, что при равенстве геометрических размеров и одинаковых поперечных усилиях для роторов, выполненных по II схеме статический прогиб примерно в два раза меньше, чем для роторов, выполненных по I схеме, а для роторов, выполненных по III схеме – в четыре раза меньше.

Таким образом, применение в конструкции объемной роторной гидромашины конкретного вида ротора заранее определяет величину его статического прогиба под действием поперечного усилия F .

Из формулы (4) следует, что величина статического прогиба существенно зависит от двух конструктивных параметров: диаметра вала – d _в и расстояния между опорами вала – l _в . По данным анализа конструкций современных аксиально-плунжерных гидромашин с наклонной шайбой с опорой блока цилиндров на валу относительные значения диаметра вала в районе шлицевого соединения составляет d _в/ d _п =1,36 ^ 1,9, а расстояние между опорами l _в / d _п = 7,47 ^ 10,4. Для всех рассмотренных гидромашин наблюдается увеличение диаметра вала и уменьшение расстояния между опорами при увеличении давления нагнетания р 2 .

Особенностью деформации вала – балки под действием поперечной силы для всех рассмотренных схем является равенство нулю угла наклона касательной к упругой линии балки в районе максимального прогиба, т.е. фх =0 при x = a. Иначе говоря, участок балки в районе максимально- го прогиба перемещается, сохраняя параллельность своей оси ее первоначальному (до деформации) положению.

Данное условие необходимо учитывать при обеспечении вынужденных перемещений блока цилиндров, для которого передней опорой является шлицевой участок вала, расположенный в зоне его максимального прогиба.

На вынужденные перемещения блока цилиндров существенное влияние оказывают одновременно передняя и задняя его опоры.

Задней опорой блока цилиндров является торцевой распределительный золотник, рабочая поверхность которого может быть плоской или сферической (рис. 4а, б). Пара блок цилиндров – поверхность распределительного золотника и в том и в другом случае принадлежит к 3-му классу, т.е. имеет три степени свободы и три связи – ограничения. Однако по виду степеней свободы и виду ограничений эти кинематические пары значительно отличаются друг от друга. Из шести степеней свободы: х , у , z - линейные перемещения вдоль соответствующих осей; ф _х , ф _у , ф ₂ -угловые перемещения относительно осей. Плоская кинематическая пара (рис.4 а ) обладает свободными перемещениями: у , z , и ф _х , (на перемещения х , ф _у , и ф ₂ - наложены связи - ограничения), а сферическая пара (рис. 4б) - перемещениями ф _х , ф _у , ф ₂ (на перемещения х , у и z - наложены связи – ограничения). Свободные перемещения торца блока цилиндров в районе распределительного золотника определяют перемещения блока в целом.

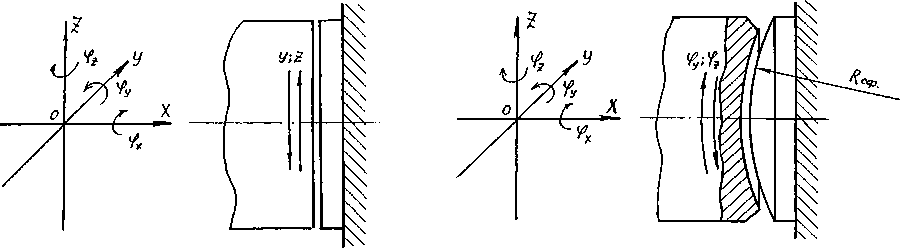
а)                                                                         б)

Рис. 4. Кинематическая пара «блок цилиндров – торцевой распределительный золотник»: а – плоская пара; б – сферическая пара

В первом случае, когда блок цилиндров опирается на плоский распределительный золотник, свободные перемещения блока в районах передней и задней опор совпадают. Поэтому отпадают какие-либо ограничения на вид центрирования шлицевого соединения «вал – блок цилиндров» – являющегося его передней опорой.

Во втором случае, когда блок цилиндров опирается на сферический распределительный золотник виды свободных перемещений блока в районах передней и задней опор получаются различными.

Для исключения возможности заклинивания блока цилиндров появляется необходимость обеспечения его угловых перемещений в районе передней опоры. Последнее может быть выполнено за счет центрирования шлицевого соединения рассматриваемых элементов по внутреннему или по наружному диаметрам при уменьшении длины зубьев на одном из элементов. При этом, для облегчения угловых перемещений блока цилиндров возможно выполнение на валу шлиц бочкообразной формы.

Наличие динамической составляющей поперечного усилия FTkх (t), ее зависимость от плунжерной частоты f пл = nz, Гц,                                        (5)

где n – скорость вращения вала, об/мин;

z – число плунжеров и кратных этой частоте гармоник, выдвигает одно из важнейших требований к конструкции ротора гидромашины – обеспечение высокой частоты его собственных колебаний – для устранения вероятности резонансных и предрезонансных условий.

Расчет и конструирование

Частота собственных изгибных колебаний вала определяется соотношением [2]

1 λk2 EJ fсоб =               , Гц ,                                         (6)

2π lв2   ρ∗ где λk – коэффициент, зависящий от условий крепления балки-вала на опорах;

k – порядок колебаний;

ρ ^∗ – масса единицы длины вала, кг ⋅ с²/см².

Преобразуем это соотношение, учитывая формулу для момента инерции сечения вала

π

J = d , тогда 64 в лk2 dв2   Eπ

2πlв2   64ρ∗, или

λ k ^{2 f} соб ⁼

2 π

d„ I    En

в

I IT J v64 p’

Из последней зависимости следует, что частота собственных колебаний вала существенно зависит от соотношения dв / lв и вида опор. По данным анализа конструкций современных аксиально-плунжерных гидромашин с наклонной шайбой с опорой блока цилиндров на валу соотношение dв / lв находится в пределах dвlв=0,17÷0,2.                                           (9)

При увеличении давления нагнетания это соотношение увеличивается.

Наиболее сильное влияние на частоту собственных колебаний вала оказывает вид опор ротора, а точнее – вид подшипников.

Ниже в табл. 2 представлены значения коэффициента λ _k для трех рассмотренных выше расчетных схем валов (для трех гармоник k = 1; 2 и 3).

Таблица 2

Вид опоры	Задний конец вала x = l	Шарнирная опора			Заделанная опора
Передний конец вала x =0	k	1	2	3	1	2	3
Шарнирная опора	λ k	π	2 π	3 π	3,927	7,069	10,210
Заделанная опора	λ k	–	–	–	4,730	7,853	10,996

Сравнение трех расчетных схем валов с учетом данных, представленных в таблице показывает, что при всех прочих равных условиях, в том числе при одном и том же значении dв / lв; вторая схема (передняя шарнирная опора и задняя – заделанная) имеет частоту собственных колебаний по первой гармонике в полтора раза большую, чем первая, а третья схема (передняя и задняя заделанные опоры) – почти в три раза большую, чем первая. Необходимым условием нормальной конструкции ротора насоса является fco61 ^ Увын1 • (10)

Если это условие не выполняется необходимо заменить общую конструктивную схему аксиальноплунжерной гидромашины на схему с самоустанавливающимся блоком цилиндров с опорой на корпусе.

Таким образом, при разработке и при проектировании аксиально-плунжерных гидромашин с наклонной шайбой с самоустанавливающимся блоком цилиндров с опорой на валу, форсированных по давлению, необходимо решение как минимум двух проблем:

• –    обеспечение работоспособности гидромашины за счет исключения раскрытия стыка между блоком цилиндров и торцевым распределительным золотником;

• –    частотная отстройка ротора гидромашины от частоты возмущающей силы (первая плунжерная гармоника).

Обе проблемы можно решить за счет:

• –    увеличения диаметра вала – d в ;

• –    уменьшения расстояния между опорами – l в ;

• –    выбора схемы ротора и вида опор, обеспечивающих минимальный статический прогиб и наивысшую частоту собственных колебаний.